DOCSLIB.ORG

Non-Parametric Vs. Parametric Tests in SAS® Venita Depuy and Paul A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Non-Parametric Vs. Parametric Tests in SAS® Venita Depuy and Paul A NESUG 17 Analysis Perusing, Choosing, and Not Mis-using: ® Non-parametric vs. Parametric Tests in SAS Venita DePuy and Paul A. Pappas, Duke Clinical Research Institute, Durham, NC ABSTRACT spread is less easy to quantify but is often represented by Most commonly used statistical procedures, such as the t- the interquartile range, which is simply the difference test, are based on the assumption of normality. The field between the first and third quartiles. of non-parametric statistics provides equivalent procedures that do not require normality, but often require DETERMINING NORMALITY assumptions such as equal variances. Parametric tests (OR LACK THEREOF) (which assume normality) are often used on non-normal One of the first steps in test selection should be data; even non-parametric tests are used when their investigating the distribution of the data. PROC assumptions are violated. This paper will provide an UNIVARIATE can be implemented to help determine overview of parametric tests and their non-parametric whether or not your data are normal. This procedure equivalents; what assumptions are required for each test; ® generates a variety of summary statistics, such as the how to perform the tests in SAS ; and guidelines for when mean and median, as well as numerical representations of both sets of assumptions are violated. properties such as skewness and kurtosis. Procedures covered will include PROCs ANOVA, CORR, If the population from which the data are obtained is NPAR1WAY, TTEST and UNIVARIATE. Discussion will normal, the mean and median should be equal or close to include assumptions and assumption violations, equal. The skewness coefficient, which is a measure of robustness, and exact versus approximate tests. symmetry, should be near zero. Positive values for the skewness coefficient indicate that the data are right INTRODUCTION skewed, and negative values indicate that that data are Many statistical tests rely heavily on distributional left skewed. The kurtosis coefficient, which is a measure assumptions, such as normality. When these of spread, should also be near zero. Positive values for assumptions are not satisfied, commonly used statistical the kurtosis coefficient indicate that the distribution of the tests often perform poorly, resulting in a greater chance of data is steeper than a normal distribution, and negative committing an error. Non-parametric tests are designed to values for kurtosis indicate that the distribution of the data have desirable statistical properties when few is flatter than normal distribution. The NORMAL option in assumptions can be made about the underlying PROC UNIVARIATE produces a table with tests for distribution of the data. In other words, when the data are normality. In general, if the p-values are less than 0.05, obtained from a non-normal distribution or one containing then the data should be considered non-normally outliers, a non-parametric test is often a more powerful distributed. However, it is important to remember that statistical tool than its parametric ‘normal theory’ these tests are heavily dependent on sample size. equivalent. Strikingly non-normal data may have a p-value greater than 0.05 due to a small sample size. Therefore, For example, the Likert scale data frequently used in graphical representations of the data should always be social sciences typically violates the assumption of examined. normality necessary for parametric tests. The ordinal scale also violates the frequent assumption that data are Low resolution plots and high resolution histograms are from a continuous distribution. Various authors (Micceri, both available in PROC UNIVARIATE. The PLOTS option Breckler) have found that, in reviews of data sets and in PROC UNIVARIATE creates low-resolution stem-and- journal articles, the majority of behavioral sciences data leaf, box, and normal probability plots. The stem-and-leaf violate the assumption of normality but rarely address that plot is used to visualize the overall distribution of the data concern. and the box plot is a graphical representation of the 5- number summary. The normal probability plot is designed In this paper, we explore the use of parametric and non- to investigate whether a variable is normally distributed. If parametric tests for one- and two-sample location the data are normal, then the plot should display a straight differences, two-sample dispersion differences, and a one diagonal line. Different departures from the straight way layout analysis. We will also examine testing for diagonal line indicate different types of departures from general differences between populations, and look at normality. different measures of correlation. The HISTOGRAM statement in PROC UNIVARIATE will MEASURES OF LOCATION AND SPREAD produce high resolution histograms. When used in Mean and variance are typically used to describe the conjunction with the NORMAL option, the histogram will center and spread of normally distributed data. If the data have a line indicating the shape of a normal distribution are not normally distributed or contain outliers, these with the same mean and variance as the sample. measures may not be robust enough to accurately PROC UNIVARIATE is an invaluable tool in visualizing describe the data. The median is a more robust measure and summarizing data in order to gain an understanding of of the center of a distribution, in that it is not as heavily the underlying populations from which the data are influenced by outliers or skewed data. As a result, the obtained. To produce these results, the following code median is typically used with non-parametric tests. The 1 NESUG 17 Analysis can be used. Omitting the VAR statement will run the If the p-value for the paired t-test is less than the specified analysis on all the variables in the dataset. alpha level, then there is evidence to suggest that the population means of the two variables differ. In the case PROC UNIVARIATE data=file1 normal plots; of measurements taken before and after a treatment, this Histogram; would suggest a treatment effect. PROC UNIVARIATE Var var1 var2...varn; Run; also calculates t-test for the difference being equal to zero, which is equivalent to the paired t-test (code given in next The determination of the normality of the data should section). result from evaluation of the graphical output in conjunction with the numerical output. In addition, the While the paired t-test is robust to departures in normality user might wish to look at subsets of the data; for when the two distributions are the same shape, the Type I example, a CLASS statement might be used to stratify by error is inflated when the distributions are skewed and gender. also have unequal variances. Therefore, care should be taken when variances appear unequal. GENERAL GUIDELINES FOR CHOOSING TESTS SIGN TEST AND SIGNED RANK TEST Obviously, if your data meets the assumptions of a The Signed Rank test and the Sign test are non- parametric test, you should use it. They are always more parametric equivalents to the one-sample paired t-test. powerful, if used appropriately. Neither of these tests requires the data to be normally If you can transform the dependent variable, such as by distributed, but both tests require that the observed differences between the paired observations be mutually using the log or square root transformation, to make it independent, and that each of the observed paired normally distributed, this may be a good alternative. ® differences comes from a continuous population SAS/INSIGHT is the easiest method to explore these options, due to its interactive nature. Manning and symmetric about a common median. However, the observed paired differences do not necessarily have to be Mullahy (2001) discuss concerns regarding obtained from the same underlying distribution. heteroscedasticity and log transformations, and the biases possible when using transformations. To calculate these tests, the difference between measurements must be calculated for each subject. This If the data are not normally distributed but the populations “difference” variable will tend to be non-zero if there is a have the same spread and similarly shaped distributions, difference between the two groups. The Sign test is and other assumptions are met, the non-parametric tests calculated by counting the number of positive differences are typically the best options. and the number of negative differences. The Signed Rank If neither the parametric nor non-parametric test test is calculated by ranking all differences by their assumptions are met, great care should be taken when absolute value, from least to greatest. If the two selecting tests. Things to consider include: differing populations do not have significantly different centers, the sample sizes, differing variances, and differing numbers of positives and negatives in the Sign test, or the distributional shapes. Zimmerman has published a variety sums of the ranks of the positive and negative numbers in of papers addressing different aspects of this, some of the Signed Rank test, should be roughly equal which are referenced. Specifics regarding each test are For small samples, the exact p-value of these tests can listed after the SAS code. manually be determined by comparing the numbers to previously determined critical values, as are found in texts DIFFERENCES IN DEPENDENT POPULATIONS such as Hollander & Wolfe. Larger sample sizes are Testing for the difference between two dependent typically calculated using a large-sample approximation.
Load more

Recommended publications
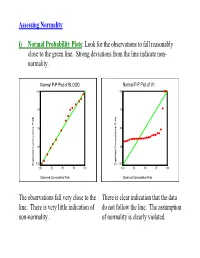
  • Assessing Normality I) Normal Probability Plots : Look for The
    Assessing Normality i) Normal Probability Plots: Look for the observations to fall reasonably close to the green line. Strong deviations from the line indicate non- normality. Normal P-P Plot of BLOOD Normal P-P Plot of V1 1.00 1.00 .75 .75 .50 .50 .25 .25 0.00 0.00 Expected Cummulative Prob Expected Cummulative Expected Cummulative Prob Expected Cummulative 0.00 .25 .50 .75 1.00 0.00 .25 .50 .75 1.00 Observed Cummulative Prob Observed Cummulative Prob The observations fall very close to the There is clear indication that the data line. There is very little indication of do not follow the line. The assumption non-normality. of normality is clearly violated. ii) Histogram: Look for a “bell-shape”. Severe skewness and/or outliers are indications of non-normality. 5 16 14 4 12 10 3 8 2 6 4 1 Std. Dev = 60.29 Std. Dev = 992.11 2 Mean = 274.3 Mean = 573.1 0 N = 20.00 0 N = 25.00 150.0 200.0 250.0 300.0 350.0 0.0 1000.0 2000.0 3000.0 4000.0 175.0 225.0 275.0 325.0 375.0 500.0 1500.0 2500.0 3500.0 4500.0 BLOOD V1 Although the histogram is not perfectly There is a clear indication that the data symmetric and bell-shaped, there is no are right-skewed with some strong clear violation of normality. outliers. The assumption of normality is clearly violated. Caution: Histograms are not useful for small sample sizes as it is difficult to get a clear picture of the distribution.
    [Show full text]
  • Heteroscedastic Errors
    Heteroscedastic Errors ◮ Sometimes plots and/or tests show that the error variances 2 σi = Var(ǫi ) depend on i ◮ Several standard approaches to fixing the problem, depending on the nature of the dependence. ◮ Weighted Least Squares. ◮ Transformation of the response. ◮ Generalized Linear Models. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Weighted Least Squares ◮ Suppose variances are known except for a constant factor. 2 2 ◮ That is, σi = σ /wi . ◮ Use weighted least squares. (See Chapter 10 in the text.) ◮ This usually arises realistically in the following situations: ◮ Yi is an average of ni measurements where you know ni . Then wi = ni . 2 ◮ Plots suggest that σi might be proportional to some power of 2 γ γ some covariate: σi = kxi . Then wi = xi− . Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Variances depending on (mean of) Y ◮ Two standard approaches are available: ◮ Older approach is transformation. ◮ Newer approach is use of generalized linear model; see STAT 402. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Transformation ◮ Compute Yi∗ = g(Yi ) for some function g like logarithm or square root. ◮ Then regress Yi∗ on the covariates. ◮ This approach sometimes works for skewed response variables like income; ◮ after transformation we occasionally find the errors are more nearly normal, more homoscedastic and that the model is simpler. ◮ See page 130ff and check under transformations and Box-Cox in the index. Richard Lockhart STAT 350: Heteroscedastic Errors and GLIM Generalized Linear Models ◮ Transformation uses the model T E(g(Yi )) = xi β while generalized linear models use T g(E(Yi )) = xi β ◮ Generally latter approach offers more flexibility.
    [Show full text]
  • Power Comparisons of the Mann-Whitney U and Permutation Tests
    Power Comparisons of the Mann-Whitney U and Permutation Tests Abstract: Though the Mann-Whitney U-test and permutation tests are often used in cases where distribution assumptions for the two-sample t-test for equal means are not met, it is not widely understood how the powers of the two tests compare. Our goal was to discover under what circumstances the Mann-Whitney test has greater power than the permutation test. The tests’ powers were compared under various conditions simulated from the Weibull distribution. Under most conditions, the permutation test provided greater power, especially with equal sample sizes and with unequal standard deviations. However, the Mann-Whitney test performed better with highly skewed data. Background and Significance: In many psychological, biological, and clinical trial settings, distributional differences among testing groups render parametric tests requiring normality, such as the z test and t test, unreliable. In these situations, nonparametric tests become necessary. Blair and Higgins (1980) illustrate the empirical invalidity of claims made in the mid-20th century that t and F tests used to detect differences in population means are highly insensitive to violations of distributional assumptions, and that non-parametric alternatives possess lower power. Through power testing, Blair and Higgins demonstrate that the Mann-Whitney test has much higher power relative to the t-test, particularly under small sample conditions. This seems to be true even when Welch’s approximation and pooled variances are used to “account” for violated t-test assumptions (Glass et al. 1972). With the proliferation of powerful computers, computationally intensive alternatives to the Mann-Whitney test have become possible.
    [Show full text]
  • Research Report Statistical Research Unit Goteborg University Sweden
    Research Report Statistical Research Unit Goteborg University Sweden Testing for multivariate heteroscedasticity Thomas Holgersson Ghazi Shukur Research Report 2003:1 ISSN 0349-8034 Mailing address: Fax Phone Home Page: Statistical Research Nat: 031-77312 74 Nat: 031-77310 00 http://www.stat.gu.se/stat Unit P.O. Box 660 Int: +4631 773 12 74 Int: +4631 773 1000 SE 405 30 G6teborg Sweden Testing for Multivariate Heteroscedasticity By H.E.T. Holgersson Ghazi Shukur Department of Statistics Jonkoping International GOteborg university Business school SE-405 30 GOteborg SE-55 111 Jonkoping Sweden Sweden Abstract: In this paper we propose a testing technique for multivariate heteroscedasticity, which is expressed as a test of linear restrictions in a multivariate regression model. Four test statistics with known asymptotical null distributions are suggested, namely the Wald (W), Lagrange Multiplier (LM), Likelihood Ratio (LR) and the multivariate Rao F-test. The critical values for the statistics are determined by their asymptotic null distributions, but also bootstrapped critical values are used. The size, power and robustness of the tests are examined in a Monte Carlo experiment. Our main findings are that all the tests limit their nominal sizes asymptotically, but some of them have superior small sample properties. These are the F, LM and bootstrapped versions of Wand LR tests. Keywords: heteroscedasticity, hypothesis test, bootstrap, multivariate analysis. I. Introduction In the last few decades a variety of methods has been proposed for testing for heteroscedasticity among the error terms in e.g. linear regression models. The assumption of homoscedasticity means that the disturbance variance should be constant (or homoscedastic) at each observation.
    [Show full text]
  • T-Statistic Based Correlation and Heterogeneity Robust Inference
    t-Statistic Based Correlation and Heterogeneity Robust Inference Rustam IBRAGIMOV Economics Department, Harvard University, 1875 Cambridge Street, Cambridge, MA 02138 Ulrich K. MÜLLER Economics Department, Princeton University, Fisher Hall, Princeton, NJ 08544 ([email protected]) We develop a general approach to robust inference about a scalar parameter of interest when the data is potentially heterogeneous and correlated in a largely unknown way. The key ingredient is the following result of Bakirov and Székely (2005) concerning the small sample properties of the standard t-test: For a significance level of 5% or lower, the t-test remains conservative for underlying observations that are independent and Gaussian with heterogenous variances. One might thus conduct robust large sample inference as follows: partition the data into q ≥ 2 groups, estimate the model for each group, and conduct a standard t-test with the resulting q parameter estimators of interest. This results in valid and in some sense efficient inference when the groups are chosen in a way that ensures the parameter estimators to be asymptotically independent, unbiased and Gaussian of possibly different variances. We provide examples of how to apply this approach to time series, panel, clustered and spatially correlated data. KEY WORDS: Dependence; Fama–MacBeth method; Least favorable distribution; t-test; Variance es- timation. 1. INTRODUCTION property of the correlations. The key ingredient to the strategy is a result by Bakirov and Székely (2005) concerning the small Empirical analyses in economics often face the difficulty that sample properties of the usual t-test used for inference on the the data is correlated and heterogeneous in some unknown fash- mean of independent normal variables: For significance levels ion.
    [Show full text]
  • Boxplots for Grouped and Clustered Data in Toxicology
    Penultimate version. If citing, please refer instead to the published version in Archives of Toxicology, DOI: 10.1007/s00204-015-1608-4. Boxplots for grouped and clustered data in toxicology Philip Pallmann1, Ludwig A. Hothorn2 1 Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, UK, Tel.: +44 (0)1524 592318, [email protected] 2 Institute of Biostatistics, Leibniz University Hannover, 30419 Hannover, Germany Abstract The vast majority of toxicological papers summarize experimental data as bar charts of means with error bars. While these graphics are easy to generate, they often obscure essen- tial features of the data, such as outliers or subgroups of individuals reacting differently to a treatment. Especially raw values are of prime importance in toxicology, therefore we argue they should not be hidden in messy supplementary tables but rather unveiled in neat graphics in the results section. We propose jittered boxplots as a very compact yet comprehensive and intuitively accessible way of visualizing grouped and clustered data from toxicological studies together with individual raw values and indications of statistical significance. A web application to create these plots is available online. Graphics, statistics, R software, body weight, micronucleus assay 1 Introduction Preparing a graphical summary is usually the first if not the most important step in a data analysis procedure, and it can be challenging especially with many-faceted datasets as they occur frequently in toxicological studies. However, even in simple experimental setups many researchers have a hard time presenting their results in a suitable manner. Browsing recent volumes of this journal, we have realized that the least favorable ways of displaying toxicological data appear to be the most popular ones (according to the number of publications that use them).
    [Show full text]
  • Two-Way Heteroscedastic ANOVA When the Number of Levels Is Large
    Two-way Heteroscedastic ANOVA when the Number of Levels is Large Short Running Title: Two-way ANOVA Lan Wang 1 and Michael G. Akritas 2 Revision: January, 2005 Abstract We consider testing the main treatment e®ects and interaction e®ects in crossed two-way layout when one factor or both factors have large number of levels. Random errors are allowed to be nonnormal and heteroscedastic. In heteroscedastic case, we propose new test statistics. The asymptotic distributions of our test statistics are derived under both the null hypothesis and local alternatives. The sample size per treatment combination can either be ¯xed or tend to in¯nity. Numerical simulations indicate that the proposed procedures have good power properties and maintain approximately the nominal ®-level with small sample sizes. A real data set from a study evaluating forty varieties of winter wheat in a large-scale agricultural trial is analyzed. Key words: heteroscedasticity, large number of factor levels, unbalanced designs, quadratic forms, projection method, local alternatives 1385 Ford Hall, School of Statistics, University of Minnesota, 224 Church Street SE, Minneapolis, MN 55455. Email: [email protected], phone: (612) 625-7843, fax: (612) 624-8868. 2414 Thomas Building, Department of Statistics, the Penn State University, University Park, PA 16802. E-mail: [email protected], phone: (814) 865-3631, fax: (814) 863-7114. 1 Introduction In many experiments, data are collected in the form of a crossed two-way layout. If we let Xijk denote the k-th response associated with the i-th level of factor A and j -th level of factor B, then the classical two-way ANOVA model speci¯es that: Xijk = ¹ + ®i + ¯j + γij + ²ijk (1.1) where i = 1; : : : ; a; j = 1; : : : ; b; k = 1; 2; : : : ; nij, and to be identi¯able the parameters Pa Pb Pa Pb are restricted by conditions such as i=1 ®i = j=1 ¯j = i=1 γij = j=1 γij = 0.
    [Show full text]
  • Profiling Heteroscedasticity in Linear Regression Models
    358 The Canadian Journal of Statistics Vol. 43, No. 3, 2015, Pages 358–377 La revue canadienne de statistique Profiling heteroscedasticity in linear regression models Qian M. ZHOU1*, Peter X.-K. SONG2 and Mary E. THOMPSON3 1Department of Statistics and Actuarial Science, Simon Fraser University, Burnaby, British Columbia, Canada 2Department of Biostatistics, University of Michigan, Ann Arbor, Michigan, U.S.A. 3Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Ontario, Canada Key words and phrases: Heteroscedasticity; hybrid test; information ratio; linear regression models; model- based estimators; sandwich estimators; screening; weighted least squares. MSC 2010: Primary 62J05; secondary 62J20 Abstract: Diagnostics for heteroscedasticity in linear regression models have been intensively investigated in the literature. However, limited attention has been paid on how to identify covariates associated with heteroscedastic error variances. This problem is critical in correctly modelling the variance structure in weighted least squares estimation, which leads to improved estimation efficiency. We propose covariate- specific statistics based on information ratios formed as comparisons between the model-based and sandwich variance estimators. A two-step diagnostic procedure is established, first to detect heteroscedasticity in error variances, and then to identify covariates the error variance structure might depend on. This proposed method is generalized to accommodate practical complications, such as when covariates associated with the heteroscedastic variances might not be associated with the mean structure of the response variable, or when strong correlation is present amongst covariates. The performance of the proposed method is assessed via a simulation study and is illustrated through a data analysis in which we show the importance of correct identification of covariates associated with the variance structure in estimation and inference.
    [Show full text]
  • Length of Stay Outlier Detection Through Cluster Analysis: a Case Study in Pediatrics Daniel Gartnera, Rema Padmanb
    Length of Stay Outlier Detection through Cluster Analysis: A Case Study in Pediatrics Daniel Gartnera, Rema Padmanb aSchool of Mathematics, Cardiff University, United Kingdom bThe H. John Heinz III College, Carnegie Mellon University, Pittsburgh, USA Abstract The increasing availability of detailed inpatient data is enabling the develop- ment of data-driven approaches to provide novel insights for the management of Length of Stay (LOS), an important quality metric in hospitals. This study examines clustering of inpatients using clinical and demographic attributes to identify LOS outliers and investigates the opportunity to reduce their LOS by comparing their order sequences with similar non-outliers in the same cluster. Learning from retrospective data on 353 pediatric inpatients admit- ted for appendectomy, we develop a two-stage procedure that first identifies a typical cluster with LOS outliers. Our second stage analysis compares orders pairwise to determine candidates for switching to make LOS outliers simi- lar to non-outliers. Results indicate that switching orders in homogeneous inpatient sub-populations within the limits of clinical guidelines may be a promising decision support strategy for LOS management. Keywords: Machine Learning; Clustering; Health Care; Length of Stay Email addresses: [email protected] (Daniel Gartner), [email protected] (Rema Padman) 1. Introduction Length of Stay (LOS) is an important quality metric in hospitals that has been studied for decades Kim and Soeken (2005); Tu et al. (1995). However, the increasing digitization of healthcare with Electronic Health Records and other clinical information systems is enabling the collection and analysis of vast amounts of data using advanced data-driven methods that may be par- ticularly valuable for LOS management Gartner (2015); Saria et al.
    [Show full text]
  • Iterative Approaches to Handling Heteroscedasticity with Partially Known Error Variances
    International Journal of Statistics and Probability; Vol. 8, No. 2; March 2019 ISSN 1927-7032 E-ISSN 1927-7040 Published by Canadian Center of Science and Education Iterative Approaches to Handling Heteroscedasticity With Partially Known Error Variances Morteza Marzjarani Correspondence: Morteza Marzjarani, National Marine Fisheries Service, Southeast Fisheries Science Center, Galveston Laboratory, 4700 Avenue U, Galveston, Texas 77551, USA. Received: January 30, 2019 Accepted: February 20, 2019 Online Published: February 22, 2019 doi:10.5539/ijsp.v8n2p159 URL: https://doi.org/10.5539/ijsp.v8n2p159 Abstract Heteroscedasticity plays an important role in data analysis. In this article, this issue along with a few different approaches for handling heteroscedasticity are presented. First, an iterative weighted least square (IRLS) and an iterative feasible generalized least square (IFGLS) are deployed and proper weights for reducing heteroscedasticity are determined. Next, a new approach for handling heteroscedasticity is introduced. In this approach, through fitting a multiple linear regression (MLR) model or a general linear model (GLM) to a sufficiently large data set, the data is divided into two parts through the inspection of the residuals based on the results of testing for heteroscedasticity, or via simulations. The first part contains the records where the absolute values of the residuals could be assumed small enough to the point that heteroscedasticity would be ignorable. Under this assumption, the error variances are small and close to their neighboring points. Such error variances could be assumed known (but, not necessarily equal).The second or the remaining portion of the said data is categorized as heteroscedastic. Through real data sets, it is concluded that this approach reduces the number of unusual (such as influential) data points suggested for further inspection and more importantly, it will lowers the root MSE (RMSE) resulting in a more robust set of parameter estimates.
    [Show full text]
  • Logistic Regression, Part I: Problems with the Linear Probability Model
    Logistic Regression, Part I: Problems with the Linear Probability Model (LPM) Richard Williams, University of Notre Dame, https://www3.nd.edu/~rwilliam/ Last revised February 22, 2015 This handout steals heavily from Linear probability, logit, and probit models, by John Aldrich and Forrest Nelson, paper # 45 in the Sage series on Quantitative Applications in the Social Sciences. INTRODUCTION. We are often interested in qualitative dependent variables: • Voting (does or does not vote) • Marital status (married or not) • Fertility (have children or not) • Immigration attitudes (opposes immigration or supports it) In the next few handouts, we will examine different techniques for analyzing qualitative dependent variables; in particular, dichotomous dependent variables. We will first examine the problems with using OLS, and then present logistic regression as a more desirable alternative. OLS AND DICHOTOMOUS DEPENDENT VARIABLES. While estimates derived from regression analysis may be robust against violations of some assumptions, other assumptions are crucial, and violations of them can lead to unreasonable estimates. Such is often the case when the dependent variable is a qualitative measure rather than a continuous, interval measure. If OLS Regression is done with a qualitative dependent variable • it may seriously misestimate the magnitude of the effects of IVs • all of the standard statistical inferences (e.g. hypothesis tests, construction of confidence intervals) are unjustified • regression estimates will be highly sensitive to the range of particular values observed (thus making extrapolations or forecasts beyond the range of the data especially unjustified) OLS REGRESSION AND THE LINEAR PROBABILITY MODEL (LPM). The regression model places no restrictions on the values that the independent variables take on.
    [Show full text]
  • Lecture 3: Heteroscedasticity
    Chapter 4 Lecture 3: Heteroscedasticity In many situations, the Gauss-Markov conditions will not be satisfied. These are: E[ǫ] = 0 i = 1,...,n ǫ X ⊥ 2 Var(ǫ)= σ In We consider the model Y = Xβ + ǫ. Suppose that, conditioned on X, ǫ has covariance matrix Var(ǫ X)= σ2Ψ | where Ψ depends on X. Recall that the OLS estimator βOLS of β is: t −1 t b t −1 t βOLS =(X X) X Y = β +(X X) X ǫ. Therefore, conditioned on X,b the covariance matrix of βOLS is: 2 t b−1 t −1 Var(βOLS X)= σ (X X) Ψ(X X) . | If Ψ = I, then the proof of the Gauss-Markov theorem, that the OLS estimator is BLUE breaks down; 6 b the OLS estimator is unbiased, but no longer best in the least squares sense. 4.1 Estimation when Ψ is known If Ψ is known, let P denote a non-singular n n matrix such that P tP =Ψ−1. Such a matrix exists × and P ΨP t = I. Consequently, E[Pǫ X] = 0 and Var(Pǫ X) = σ2I, which does not depend on X. | | It follows that the Gauss-Markov conditions are satisfied for Pǫ. The entire model may therefore be transformed: 41 PY = PXβ + Pǫ which may be written as: Y ∗ = X∗β + ǫ∗. This model satisfies the Gauss Markov conditions and the resulting estimator, which is BLUE, is: ∗t ∗ −1 ∗t t −1 −1 t −1 βGLS =(X X ) X Y =(X Ψ X) X Ψ Y. Here GLS stands for Generlisedb Least Squares.
    [Show full text]