DOCSLIB.ORG

Differential Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Differential Geometry DIFFERENTIAL GEOMETRY RUI LOJA FERNANDES Date: May 11, 2021. 1 Contents Part 1. Basic Concepts 5 0. Manifolds as subsets of Euclidean space 7 1. Abstract Manifolds 12 2. Manifolds with Boundary 19 3. Partitions of Unity 23 4. The Tangent Space 27 5. The Differential 35 6. Immersions, Submersions and Submanifolds 38 7. Embeddings and Whitney’s Theorem 47 8. Foliations 55 9. Quotients 64 Part 2. Lie Theory 74 10. Vector Fields and Flows 75 11. Lie Bracket and Lie Derivative 83 12. Distributions and the Frobenius Theorem 88 13. Lie Groups and Lie Algebras 93 14. Integrations of Lie Algebras 100 15. The Exponential Map 106 16. Groups of Transformations 110 Part 3. Differential Forms 120 17. Differential Forms and Tensor Fields 122 18. Differential and Cartan Calculus 132 19. Integration on Manifolds 138 20. de Rham Cohomology 144 21. The de Rham Theorem 150 22. Homotopy Invariance and Mayer-Vietoris Sequence 158 23. Computations in Cohomology 168 24. The Degree and the Index 178 Part 4. Fiber Bundles 186 25. Vector Bundles 188 26. The Thom Class and the Euler Class 197 27. Pullbacks of Vector Bundles 207 28. The Classification of Vector Bundles 213 29. Connections and Parallel Transport 217 30. Curvature and Holonomy 225 31. The Chern-Weil homomorphism 231 32. Characteristic Classes 238 33. Fiber Bundles 248 34. Principal Fiber Bundles 255 2 Preface These are lecture notes for the courses “Differentiable Manifolds I” and “Differentiable Manifolds II”, that I am lecturing at UIUC. This course is usually taken by graduate students in Mathematics in their first or second year of studies. The background for this course is a basic knowledge of analysis, algebra and topology. My main aim in writing up these lectures notes is to offer a written version of the lectures. This should give a chance to students to concentrate more on the class, without worrying about taking notes. It offers also a guide for what material was covered in class. These notes do not replace the recommended texts for this course, quite the contrary: I hope they will be a stimulus for the students to consult those works. In fact, some of these notes follow the material in theses texts. These notes are organized into sections, each of these should correspond to lectures of approximately to 1 hour and 30 minutes of classroom time. However, some sections do include more material than others, which corre- spond to different rhythms in class. The exercises at the end of each section are a very important part of the course, since one learns a good deal about mathematics by solving exercises. Moreover, sometimes the exercises con- tain results that were mentioned in class, but not proved, and which are used in later sections. The students should also keep in mind that the exercises are not homogeneous: this is in line with the fact that in mathematics when one faces for the first time a problem, one usually does not know if it has an easy solution, a hard solution or if it is an open problem. These notes are a modified version of similar lectures notes in Portuguese that I have used at IST-Lisbon. For the Portuguese version I have profited from comments from Ana Rita Pires, Georgios Kydonakis, Miguel Negr˜ao, Miguel Olmos, Ricardo Inglˆes, Ricardo Joel, Jos´eNat´ario and Roger Picken. A special thanks goes to my colleague from IST Silvia Anjos, who has pointed out many typos and mistakes, and has suggested several corrections. I continue to update these notes and I will be grateful for any corrections and suggestions for improvement that are sent to me. Rui Loja Fernandes [email protected] Department of Mathematics, UIUC Urbana IL, USA 3 4 Part 1. Basic Concepts The notion of a smooth manifold of dimension d makes precise the con- cept of a space which locally looks like the usual euclidean space Rd. Hence, it generalizes the usual notions of curve (locally looks like R1) and surface (locally looks like R2). This course consists of a precise study of this fun- damental concept of Mathematics and some of the constructions associated with it. We will see that many constructions familiar in infinitesimal anal- ysis (i.e., calculus) extend from euclidean space to smooth manifolds. On the other hand, the global analysis of manifolds requires new techniques and methods, and often elementary questions lead to open problems. In this first part of the lectures we will introduce the most basic concepts of Differential Geometry, starting with the precise notion of a smooth manifold. The main concepts and ideas to keep in mind from these first part are: Section 0: A manifold as a subset of Euclidean space, and the various • categories of manifolds: topological, smooth and analytic manifolds. Section 1: The abstract notion of smooth manifold (our objects) and • smooth map (our morphisms). Section 2: A technique of gluing called partitions of unity. • Section 3: Manifolds with boundary and smooth maps between man- • ifolds with boundary. Section 4: Tangent vector, tangent space (our infinitesimal objects). • Section 5: The differential of a smooth map (our infinitesimal mor- • phisms). Section 6: Important classes of smooth maps: immersions, submer- • sions and local difeomorphisms. Submanifolds (our sub-objects). Section 7: Embedded sub manifolds and the Whitney Embedding The- • orem, showing that any smooth manifold can be embedded in some Euclidean space Rn. Section 8 Foliations, which are certain partitions of a manifold into • submanifolds, a very useful generalization of the notion of manifold. Section 9: Quotients of manifolds, i.e., smooth manifolds obtained • from other smooth manifolds by taking equivalence relations. 5 6 0. Manifolds as subsets of Euclidean space Recall that the Euclidean space of dimension n is: Rn := (x1,...,xn) : x1,...,xn R ∈ We will also denote by xi: Rn R the i-th coordinate function in Rn. If U Rn is an open set, a map f→: U Rm is called a smooth map if all its⊂ partials derivatives of every order:→ ∂rf j (x), ∂xi1 ∂xir · · · exist and are continuous functions in U. More generally, given any subset X Rn and a map f : X Rm, where X is not necessarily an open set, we say⊂ that f is a smooth map→ if for each x X there is an open neighborhood n m ∈ U R and a smooth map F : U R such that f X U = F X U . ⊂A very basic property which we→ leave as an exercise| ∩ is that:| ∩ Proposition 0.1. Let X Rn, Y Rm and Z Rp. If f : X Y and g : Y Z are smooth maps,⊂ then g ⊂f : X Z is⊂ also a smooth→ map. → ◦ → A bijection f : X Y , where X Rn and Y Rm, with inverse 1 → ⊂ 1 ⊂ map f − : Y X, such that both f and f − are smooth, is called a diffeomorphism→ and we say that X and Y are diffeomorphic subsets. Rm Rn f Y X One would like to study properties of sets which are invariant under dif- feomorphisms, characterize classes of sets invariant under diffeomorphisms, etc. However, in this definition, the sets X and Y are just too general, and it is hopeless to try to say anything interesting about classes of such diffeo- morphic subsets. One must consider nicer subsets of Euclidean space: for example, it is desirable that the subset has at each point a tangent space and that the tangent spaces vary smoothly. Recall that a subset X Rn has an induced topology, called the relative topology, where the relative⊂ open sets are just the sets of the form X U, where U Rn is an open set. ∩ ⊂ Definition 0.2. A subset M Rn is called a smooth manifold of di- mension d if each p M has a⊂ neighborhood M U which is diffeomorphic to an open set V R∈d. ∩ ⊂ 7 The diffeomorphism φ : M U V , in this definition, is called a coor- ∩ → 1 dinate system. The inverse map φ− : V M U, which by assumption is smooth, is called a parameterization. → ∩ Rn M U U M ∩ φ Rd V We have the category of smooth manifolds where: the objects are smooth manifolds; • the morphisms are smooth maps. • The reason they form a category is because the composition of smooth maps is a smooth map and the identity is also a smooth map. Examples 0.3. 1. Any open subset U Rd is itself a smooth manifold of dimension d: the .inclusion i : U ֒ Rd gives⊂ a global defined coordinate chart → 2. If f : Rd Rm is any smooth map, its graph: → Graph(f) := (x, f(x)) : x Rd Rd+m { ∈ }⊂ is a smooth manifold of dimension d: the map x (x, f(x)) is a diffeomor- phism Rd Graph(M), so gives a global parametrization7→ of Graph(f). → Rm (x, f(x)) R d 8 3. The unit d-sphere is the subset of Rd+1 formed by all vectors of length 1: Sd := x Rd+1 : x =1 . { ∈ || || } This is a d-dimensional manifold which does not admit a global parametriza- tion. However we can cover the sphere by two coordinate systems: if we let N = (0,..., 0, 1) and S = (0,..., 0, 1) denote the north and south poles, then stereographic projection relative to− N and S give two coordinate systems π : Sd N Rd and π : Sd S Rd. Ø× N −{ } → S −{ } →ÈËÖ Å Í « d Í Ë ¬ Æ « ¬ ½ Æ ¬ « Ô ½ Æ « ¬ d ´Ôµ Æ Ê 4. The only connected manifolds of dimension 1 are the line R and the circle S1.
Load more

Recommended publications
  • Algebraic Equations for Nonsmoothable 8-Manifolds
    PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. NICHOLAAS H. KUIPER Algebraic equations for nonsmoothable 8-manifolds Publications mathématiques de l’I.H.É.S., tome 33 (1967), p. 139-155 <http://www.numdam.org/item?id=PMIHES_1967__33__139_0> © Publications mathématiques de l’I.H.É.S., 1967, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http:// www.ihes.fr/IHES/Publications/Publications.html) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou im- pression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ ALGEBRAIC EQUATIONS FOR NONSMOOTHABLE 8-MANIFOLDS by NICOLAAS H. KUIPER (1) SUMMARY The singularities of Brieskorn and Hirzebruch are used in order to obtain examples of algebraic varieties of complex dimension four in P^C), which are homeo- morphic to closed combinatorial 8-manifolds, but not homeomorphic to any differentiable manifold. Analogous nonorientable real algebraic varieties of dimension 8 in P^R) are also given. The main theorem states that every closed combinatorial 8-manifbld is homeomorphic to a Nash-component with at most one singularity of some real algebraic variety. This generalizes the theorem of Nash for differentiable manifolds. § i. Introduction. The theorem of Wall. From the smoothing theory of Thorn [i], Munkres [2] and others and the knowledge of the groups of differential structures on spheres due to Kervaire, Milnor [3], Smale and Gerf [4] follows a.o.
    [Show full text]
  • An Introduction to Differentiable Manifolds
    Mathematics Letters 2016; 2(5): 32-35 http://www.sciencepublishinggroup.com/j/ml doi: 10.11648/j.ml.20160205.11 Conference Paper An Introduction to Differentiable Manifolds Kande Dickson Kinyua Department of Mathematics, Moi University, Eldoret, Kenya Email address: [email protected] To cite this article: Kande Dickson Kinyua. An Introduction to Differentiable Manifolds. Mathematics Letters. Vol. 2, No. 5, 2016, pp. 32-35. doi: 10.11648/j.ml.20160205.11 Received : September 7, 2016; Accepted : November 1, 2016; Published : November 23, 2016 Abstract: A manifold is a Hausdorff topological space with some neighborhood of a point that looks like an open set in a Euclidean space. The concept of Euclidean space to a topological space is extended via suitable choice of coordinates. Manifolds are important objects in mathematics, physics and control theory, because they allow more complicated structures to be expressed and understood in terms of the well–understood properties of simpler Euclidean spaces. A differentiable manifold is defined either as a set of points with neighborhoods homeomorphic with Euclidean space, Rn with coordinates in overlapping neighborhoods being related by a differentiable transformation or as a subset of R, defined near each point by expressing some of the coordinates in terms of the others by differentiable functions. This paper aims at making a step by step introduction to differential manifolds. Keywords: Submanifold, Differentiable Manifold, Morphism, Topological Space manifolds with the additional condition that the transition 1. Introduction maps are analytic. In other words, a differentiable (or, smooth) The concept of manifolds is central to many parts of manifold is a topological manifold with a globally defined geometry and modern mathematical physics because it differentiable (or, smooth) structure, [1], [3], [4].
    [Show full text]
  • Graphs and Patterns in Mathematics and Theoretical Physics, Volume 73
    http://dx.doi.org/10.1090/pspum/073 Graphs and Patterns in Mathematics and Theoretical Physics This page intentionally left blank Proceedings of Symposia in PURE MATHEMATICS Volume 73 Graphs and Patterns in Mathematics and Theoretical Physics Proceedings of the Conference on Graphs and Patterns in Mathematics and Theoretical Physics Dedicated to Dennis Sullivan's 60th birthday June 14-21, 2001 Stony Brook University, Stony Brook, New York Mikhail Lyubich Leon Takhtajan Editors Proceedings of the conference on Graphs and Patterns in Mathematics and Theoretical Physics held at Stony Brook University, Stony Brook, New York, June 14-21, 2001. 2000 Mathematics Subject Classification. Primary 81Txx, 57-XX 18-XX 53Dxx 55-XX 37-XX 17Bxx. Library of Congress Cataloging-in-Publication Data Stony Brook Conference on Graphs and Patterns in Mathematics and Theoretical Physics (2001 : Stony Brook University) Graphs and Patterns in mathematics and theoretical physics : proceedings of the Stony Brook Conference on Graphs and Patterns in Mathematics and Theoretical Physics, June 14-21, 2001, Stony Brook University, Stony Brook, NY / Mikhail Lyubich, Leon Takhtajan, editors. p. cm. — (Proceedings of symposia in pure mathematics ; v. 73) Includes bibliographical references. ISBN 0-8218-3666-8 (alk. paper) 1. Graph Theory. 2. Mathematics-Graphic methods. 3. Physics-Graphic methods. 4. Man• ifolds (Mathematics). I. Lyubich, Mikhail, 1959- II. Takhtadzhyan, L. A. (Leon Armenovich) III. Title. IV. Series. QA166.S79 2001 511/.5-dc22 2004062363 Copying and reprinting. Material in this book may be reproduced by any means for edu• cational and scientific purposes without fee or permission with the exception of reproduction by services that collect fees for delivery of documents and provided that the customary acknowledg• ment of the source is given.
    [Show full text]
  • A Comparison of Differential Calculus and Differential Geometry in Two
    1 A Two-Dimensional Comparison of Differential Calculus and Differential Geometry Andrew Grossfield, Ph.D Vaughn College of Aeronautics and Technology Abstract and Introduction: Plane geometry is mainly the study of the properties of polygons and circles. Differential geometry is the study of curves that can be locally approximated by straight line segments. Differential calculus is the study of functions. These functions of calculus can be viewed as single-valued branches of curves in a coordinate system where the horizontal variable controls the vertical variable. In both studies the derivative multiplies incremental changes in the horizontal variable to yield incremental changes in the vertical variable and both studies possess the same rules of differentiation and integration. It seems that the two studies should be identical, that is, isomorphic. And, yet, students should be aware of important differences. In differential geometry, the horizontal and vertical units have the same dimensional units. In differential calculus the horizontal and vertical units are usually different, e.g., height vs. time. There are differences in the two studies with respect to the distance between points. In differential geometry, the Pythagorean slant distance formula prevails, while in the 2- dimensional plane of differential calculus there is no concept of slant distance. The derivative has a different meaning in each of the two subjects. In differential geometry, the slope of the tangent line determines the direction of the tangent line; that is, the angle with the horizontal axis. In differential calculus, there is no concept of direction; instead, the derivative describes a rate of change. In differential geometry the line described by the equation y = x subtends an angle, α, of 45° with the horizontal, but in calculus the linear relation, h = t, bears no concept of direction.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
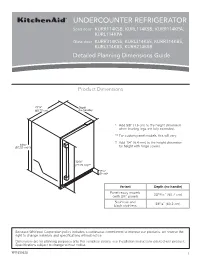
  • Dimension Guide
    UNDERCOUNTER REFRIGERATOR Solid door KURR114KSB, KURL114KSB, KURR114KPA, KURL114KPA Glass door KURR314KSS, KURL314KSS, KURR314KBS, KURL314KBS, KURR214KSB Detailed Planning Dimensions Guide Product Dimensions 237/8” Depth (60.72 cm) (no handle) * Add 5/8” (1.6 cm) to the height dimension when leveling legs are fully extended. ** For custom panel models, this will vary. † Add 1/4” (6.4 mm) to the height dimension 343/8” (87.32 cm)*† for height with hinge covers. 305/8” (77.75 cm)** 39/16” (9 cm)* Variant Depth (no handle) Panel ready models 2313/16” (60.7 cm) (with 3/4” panel) Stainless and 235/8” (60.2 cm) black stainless Because Whirlpool Corporation policy includes a continuous commitment to improve our products, we reserve the right to change materials and specifications without notice. Dimensions are for planning purposes only. For complete details, see Installation Instructions packed with product. Specifications subject to change without notice. W11530525 1 Panel ready models Stainless and black Dimension Description (with 3/4” panel) stainless models A Width of door 233/4” (60.3 cm) 233/4” (60.3 cm) B Width of the grille 2313/16” (60.5 cm) 2313/16” (60.5 cm) C Height to top of handle ** 311/8” (78.85 cm) Width from side of refrigerator to 1 D handle – door open 90° ** 2 /3” (5.95 cm) E Depth without door 2111/16” (55.1 cm) 2111/16” (55.1 cm) F Depth with door 2313/16” (60.7 cm) 235/8” (60.2 cm) 7 G Depth with handle ** 26 /16” (67.15 cm) H Depth with door open 90° 4715/16” (121.8 cm) 4715/16” (121.8 cm) **For custom panel models, this will vary.
    [Show full text]
  • Riemann's Contribution to Differential Geometry
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Historia Mathematics 9 (1982) l-18 RIEMANN'S CONTRIBUTION TO DIFFERENTIAL GEOMETRY BY ESTHER PORTNOY UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN, URBANA, IL 61801 SUMMARIES In order to make a reasonable assessment of the significance of Riemann's role in the history of dif- ferential geometry, not unduly influenced by his rep- utation as a great mathematician, we must examine the contents of his geometric writings and consider the response of other mathematicians in the years immedi- ately following their publication. Pour juger adkquatement le role de Riemann dans le developpement de la geometric differentielle sans etre influence outre mesure par sa reputation de trks grand mathematicien, nous devons &udier le contenu de ses travaux en geometric et prendre en consideration les reactions des autres mathematiciens au tours de trois an&es qui suivirent leur publication. Urn Riemann's Einfluss auf die Entwicklung der Differentialgeometrie richtig einzuschZtzen, ohne sich von seinem Ruf als bedeutender Mathematiker iiberm;issig beeindrucken zu lassen, ist es notwendig den Inhalt seiner geometrischen Schriften und die Haltung zeitgen&sischer Mathematiker unmittelbar nach ihrer Verijffentlichung zu untersuchen. On June 10, 1854, Georg Friedrich Bernhard Riemann read his probationary lecture, "iber die Hypothesen welche der Geometrie zu Grunde liegen," before the Philosophical Faculty at Gdttingen ill. His biographer, Dedekind [1892, 5491, reported that Riemann had worked hard to make the lecture understandable to nonmathematicians in the audience, and that the result was a masterpiece of presentation, in which the ideas were set forth clearly without the aid of analytic techniques.
    [Show full text]
  • Spectral Dimensions and Dimension Spectra of Quantum Spacetimes
    PHYSICAL REVIEW D 102, 086003 (2020) Spectral dimensions and dimension spectra of quantum spacetimes † Michał Eckstein 1,2,* and Tomasz Trześniewski 3,2, 1Institute of Theoretical Physics and Astrophysics, National Quantum Information Centre, Faculty of Mathematics, Physics and Informatics, University of Gdańsk, ulica Wita Stwosza 57, 80-308 Gdańsk, Poland 2Copernicus Center for Interdisciplinary Studies, ulica Szczepańska 1/5, 31-011 Kraków, Poland 3Institute of Theoretical Physics, Jagiellonian University, ulica S. Łojasiewicza 11, 30-348 Kraków, Poland (Received 11 June 2020; accepted 3 September 2020; published 5 October 2020) Different approaches to quantum gravity generally predict that the dimension of spacetime at the fundamental level is not 4. The principal tool to measure how the dimension changes between the IR and UV scales of the theory is the spectral dimension. On the other hand, the noncommutative-geometric perspective suggests that quantum spacetimes ought to be characterized by a discrete complex set—the dimension spectrum. We show that these two notions complement each other and the dimension spectrum is very useful in unraveling the UV behavior of the spectral dimension. We perform an extended analysis highlighting the trouble spots and illustrate the general results with two concrete examples: the quantum sphere and the κ-Minkowski spacetime, for a few different Laplacians. In particular, we find that the spectral dimensions of the former exhibit log-periodic oscillations, the amplitude of which decays rapidly as the deformation parameter tends to the classical value. In contrast, no such oscillations occur for either of the three considered Laplacians on the κ-Minkowski spacetime. DOI: 10.1103/PhysRevD.102.086003 I.
    [Show full text]
  • Zero-Dimensional Symmetry
    Snapshots of modern mathematics № 3/2015 from Oberwolfach Zero-dimensional symmetry George Willis This snapshot is about zero-dimensional symmetry. Thanks to recent discoveries we now understand such symmetry better than previously imagined possible. While still far from complete, a picture of zero-dimen- sional symmetry is beginning to emerge. 1 An introduction to symmetry: spinning globes and infinite wallpapers Let’s begin with an example. Think of a sphere, for example a globe’s surface. Every point on it is specified by two parameters, longitude and latitude. This makes the sphere a two-dimensional surface. You can rotate the globe along an axis through the center; the object you obtain after the rotation still looks like the original globe (although now maybe New York is where the Mount Everest used to be), meaning that the sphere has rotational symmetry. Each rotation is prescribed by the latitude and longitude where the axis cuts the southern hemisphere, and by an angle through which it rotates the sphere. 1 These three parameters specify all rotations of the sphere, which thus has three-dimensional rotational symmetry. In general, a symmetry may be viewed as being a transformation (such as a rotation) that leaves an object looking unchanged. When one transformation is followed by a second, the result is a third transformation that is called the product of the other two. The collection of symmetries and their product 1 Note that we include the rotation through the angle 0, that is, the case where the globe actually does not rotate at all. 1 operation forms an algebraic structure called a group 2 .
    [Show full text]
  • Relativistic Spacetime Structure
    Relativistic Spacetime Structure Samuel C. Fletcher∗ Department of Philosophy University of Minnesota, Twin Cities & Munich Center for Mathematical Philosophy Ludwig Maximilian University of Munich August 12, 2019 Abstract I survey from a modern perspective what spacetime structure there is according to the general theory of relativity, and what of it determines what else. I describe in some detail both the “standard” and various alternative answers to these questions. Besides bringing many underexplored topics to the attention of philosophers of physics and of science, metaphysicians of science, and foundationally minded physicists, I also aim to cast other, more familiar ones in a new light. 1 Introduction and Scope In the broadest sense, spacetime structure consists in the totality of relations between events and processes described in a spacetime theory, including distance, duration, motion, and (more gener- ally) change. A spacetime theory can attribute more or less such structure, and some parts of that structure may determine other parts. The nature of these structures and their relations of determi- nation bear on the interpretation of the theory—what the world would be like if the theory were true (North, 2009). For example, the structures of spacetime might be taken as its ontological or conceptual posits, and the determination relations might indicate which of these structures is more fundamental (North, 2018). Different perspectives on these questions might also reveal structural similarities with other spacetime theories, providing the resources to articulate how the picture of the world that that theory provides is different (if at all) from what came before, and might be different from what is yet to come.1 ∗Juliusz Doboszewski, Laurenz Hudetz, Eleanor Knox, J.
    [Show full text]
  • A CONCISE MINI HISTORY of GEOMETRY 1. Origin And
    Kragujevac Journal of Mathematics Volume 38(1) (2014), Pages 5{21. A CONCISE MINI HISTORY OF GEOMETRY LEOPOLD VERSTRAELEN 1. Origin and development in Old Greece Mathematics was the crowning and lasting achievement of the ancient Greek cul- ture. To more or less extent, arithmetical and geometrical problems had been ex- plored already before, in several previous civilisations at various parts of the world, within a kind of practical mathematical scientific context. The knowledge which in particular as such first had been acquired in Mesopotamia and later on in Egypt, and the philosophical reflections on its meaning and its nature by \the Old Greeks", resulted in the sublime creation of mathematics as a characteristically abstract and deductive science. The name for this science, \mathematics", stems from the Greek language, and basically means \knowledge and understanding", and became of use in most other languages as well; realising however that, as a matter of fact, it is really an art to reach new knowledge and better understanding, the Dutch term for mathematics, \wiskunde", in translation: \the art to achieve wisdom", might be even more appropriate. For specimens of the human kind, \nature" essentially stands for their organised thoughts about sensations and perceptions of \their worlds outside and inside" and \doing mathematics" basically stands for their thoughtful living in \the universe" of their idealisations and abstractions of these sensations and perceptions. Or, as Stewart stated in the revised book \What is Mathematics?" of Courant and Robbins: \Mathematics links the abstract world of mental concepts to the real world of physical things without being located completely in either".
    [Show full text]
  • Differential Geometry Lecture 17: Geodesics and the Exponential
    Differential geometry Lecture 17: Geodesics and the exponential map David Lindemann University of Hamburg Department of Mathematics Analysis and Differential Geometry & RTG 1670 3. July 2020 David Lindemann DG lecture 17 3. July 2020 1 / 44 1 Geodesics 2 The exponential map 3 Geodesics as critical points of the energy functional 4 Riemannian normal coordinates 5 Some global Riemannian geometry David Lindemann DG lecture 17 3. July 2020 2 / 44 Recap of lecture 16: constructed covariant derivatives along curves defined parallel transport studied the relation between a given connection in the tangent bundle and its parallel transport maps introduced torsion tensor and metric connections, studied geometric interpretation defined the Levi-Civita connection of a pseudo-Riemannian manifold David Lindemann DG lecture 17 3. July 2020 3 / 44 Geodesics Recall the definition of the acceleration of a smooth curve n 00 n γ : I ! R , that is γ 2 Γγ (T R ). Question: Is there a coordinate-free analogue of this construc- tion involving connections? Answer: Yes, uses covariant derivative along curves. Definition Let M be a smooth manifold, r a connection in TM ! M, 0 and γ : I ! M a smooth curve. Then rγ0 γ 2 Γγ (TM) is called the acceleration of γ (with respect to r). Of particular interest is the case if the acceleration of a curve vanishes, that is if its velocity vector field is parallel: Definition A smooth curve γ : I ! M is called geodesic with respect to a 0 given connection r in TM ! M if rγ0 γ = 0. David Lindemann DG lecture 17 3.
    [Show full text]