DOCSLIB.ORG

Verifying Bit-Manipulations of Floating-Point

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Verifying Bit-Manipulations of Floating-Point Verifying Bit-Manipulations of Floating-Point Wonyeol Lee Rahul Sharma Alex Aiken Stanford University, USA fwonyeol, sharmar, [email protected] Abstract tomated verification technique is capable of analyzing these Reasoning about floating-point is difficult and becomes only implementations. In this paper, we present a first step to- more so if there is an interplay between floating-point and wards addressing this challenge. bit-level operations. Even though real-world floating-point Bit-precise floating-point reasoning is hard: floating- libraries use implementations that have such mixed compu- point is an approximation to real arithmetic, but floating- tations, no systematic technique to verify the correctness of point numbers do not obey the algebraic axioms of real the implementations of such computations is known. In this numbers due to rounding errors. The situation becomes even paper, we present the first general technique for verifying the more difficult in the presence of bit-level operations, such as correctness of mixed binaries, which combines abstraction, bit-manipulations of the floating-point representation. To il- lustrate a mixed code, consider an implementation that com- analytical optimization, and testing. The technique provides n a method to compute an error bound of a given implementa- putes the floating-point number 2 from a small integer n.A na¨ıve implementation would first compute the integer repre- tion with respect to its mathematical specification. We apply n our technique to Intel’s implementations of transcendental senting 2 and then perform the computationally expensive functions and prove formal error bounds for these widely operation of converting an integer to a floating-point num- used routines. ber. Alternatively, the same result can be obtained by bit- shifting n + 1023 left by 52 bits (Figure 3). Existing static Categories and Subject Descriptors D.2.4 [Software/Pro- analyses for floating-point arithmetic would be stumped by gram Verification]: Correctness proofs the bit-shift operation and would fail to prove the functional Keywords Verification; Floating-point; Bit-manipulation; correctness of this trick. Moreover, such tricks are routine in Bit-level operation; ULP error; Absolute error; x86 binary; real codes [9, 16]. Binary analysis; Transcendental function Before explaining our solution, it is important to under- stand why existing automated techniques (based on testing, 1. Introduction model checking, and abstract interpretation) are inadequate. The simplest verification technique is exhaustive testing of Highly optimized implementations of floating-point libraries all possible inputs. This approach is feasible for a function rely on intermixing floating-point and bit-level code. Even like expf that computes the exponential of a 32-bit sin- though such code is part of widely used libraries, such as gle precision floating-point number. However, the number optimized implementations of C math libraries, automatic of double precision floating-point numbers is too large for formal verification of these implementations has remained brute force enumeration to be tractable. an open challenge [22]. Although it has been demonstrated A plausible verification strategy involves encoding cor- that it is possible to construct machine-checkable proofs of rectness as the validity of a SMT formula [5]. However, correctness by hand for floating-point algorithms of the level the specifications of interest here are transcendentals and of sophistication we are interested in [11, 12], no existing au- these (ex, sin (x) ; etc.) cannot be encoded precisely in exist- ing SMT theories. Verifiers based on abstract interpretation, such as ASTREE´ and FLUCTUAT, use pattern matching to handle certain bit-trick routines in commercial floating-point avionics codes [9, 16]. Our goal is a general technique. Our approach to the problem is to divide and conquer. For a given floating-point implementation, we consider non- overlapping intervals that are subsets of the possible range of inputs. We require each interval I to satisfy the following property: if we statically know that the inputs are restricted to I, the bit-level operations can be removed from the im- plementation by partial evaluation. Then, for each interval, 1 vmovddup %xmm0, %xmm0 we have a specialized implementation that is composed ex- 2 vmulpd L2E, %xmm0, %xmm2 clusively of floating-point operations and thus amenable to 3 vroundpd $0, %xmm2, %xmm2 abstraction-based techniques. Our main contribution is to 4 vcvtpd2dqx %xmm2, %xmm3 devise a procedure to construct such intervals (x4). There 5 vpaddd B, %xmm3, %xmm3 6 vpslld $20, %xmm3, %xmm3 is one significant subtlety: The intervals do not always fully 7 vpshufd $114, %xmm3, %xmm3 cover the space and we must deal with potential “gaps” be- 8 vmulpd C1, %xmm2, %xmm1 tween intervals. Commercial tools such as FLUCTUAT [7, 9] 9 vmulpd C2, %xmm2, %xmm2 also subdivide the input range (with no gaps) to improve pre- 10 vaddpd %xmm1, %xmm0, %xmm1 cision and our technique can be seen as a systematic method 11 vaddpd %xmm2, %xmm1, %xmm1 12 vmovapd T1, %xmm0 to construct these subdivisions. We analyze the implementa- 13 vmulpd T12, %xmm1, %xmm2 tions specialized for each interval and report the maximum 14 vaddpd T11, %xmm2, %xmm2 error between the implementation and the ideal mathemati- 15 vmulpd %xmm1, %xmm2, %xmm2 cal specification. 16 vaddpd T10, %xmm2, %xmm2 17 vmulpd %xmm1, %xmm2, %xmm2 We make the following contributions. 18 vaddpd T9, %xmm2, %xmm2 • We describe the first general technique for verification 19 vmulpd %xmm1, %xmm2, %xmm2 20 vaddpd T8, %xmm2, %xmm2 of mixed floating-point and bit-level code. We are un- 21 vmulpd %xmm1, %xmm2, %xmm2 aware of any automatic or semi-automatic verification 22 vaddpd T7, %xmm2, %xmm2 technique that can prove the functional correctness of the 23 vmulpd %xmm1, %xmm2, %xmm2 production grade benchmarks we consider. Prior to this 24 vaddpd T6, %xmm2, %xmm2 25 vmulpd %xmm1, %xmm2, %xmm2 work, formal verification of such benchmarks required 26 vaddpd T5, %xmm2, %xmm2 manual construction of machine-checkable proofs [11, 27 vmulpd %xmm1, %xmm2, %xmm2 12]. 28 vaddpd T4, %xmm2, %xmm2 29 vmulpd %xmm1, %xmm2, %xmm2 • We reduce the problem of computing bounds on numeri- 30 vaddpd T3, %xmm2, %xmm2 cal errors to an optimization problem and leverage state- 31 vmulpd %xmm1, %xmm2, %xmm2 of-the-art techniques for analytical optimization. While 32 vaddpd T2, %xmm2, %xmm2 33 vmulpd %xmm1, %xmm2, %xmm2 our method is not fully automatic, these techniques auto- 34 vaddpd %xmm0, %xmm2, %xmm2 mate one of the most difficult aspects of the problem and 35 vmulpd %xmm1, %xmm2, %xmm1 make verification of complex implementations feasible. 36 vaddpd %xmm0, %xmm1, %xmm0 37 vmulpd %xmm3, %xmm0, %xmm0 • Our technique performs verification at the binary level, 38 retq not on source code or a model of the program. Thus, the derived bounds apply to the actual code that executes Figure 1. The x86 assembly code of exp that ships with directly on the hardware. S3D [3]. Instructions have been reordered to aid understand- We evaluate our technique on three implementations of ing, without affecting the output. transcendental functions from Intel’s libraries: a bounded periodic function (sin, x5.2), an unbounded discontinuous sulting proof scripts can be quite hard to read, and in periodic function (tan, x5.3), and an unbounded continu- some cases hard to modify to prove a slightly different ous function (log, x5.4). We are able to successfully bound theorem. the difference between the result computed by these imple- mentations and the exact mathematical result. For each of The rest of the paper is organized as follows. x2, through these functions, we also trade precision for performance and an example, discusses our verification technique. x3 reviews create significantly more efficient variants that produce ap- formal definitions of rounding errors and x4 presents our proximately correct results. Using our technique, we are able verification technique that combines abstraction, analytical to provide a bound on the difference between the approx- optimization, and testing. x5 discusses evaluation and x6 imate variants and the mathematical specifications. These surveys prior work. Finally, x7 gives a discussion of future results demonstrate the generality of our technique and ad- work and x8 concludes. dress some of the drawbacks of manually constructed proofs: modifying the manual proofs to prove even slightly different 2. Motivating Example theorems is difficult [11, 12]. To quote Harrison [11], S3D [3] is a combustion chemistry simulation that is heavily [N]ontrivial proofs, as are carried out in the work de- used in research on developing more efficient and cleaner scribed here, often require long and complicated se- fuels for internal combustion engines. The performance of quence of rules. The construction of these proofs often the exponential function is so important for this task that the requires considerable persistence. Moreover, the re- developers ship a hand-coded x86 assembly implementation 1 vmulpd L2E, %xmm0, %xmm2 Next, we relate this algorithm with Figure 1. Our descrip- 2 vroundpd $0xfffffffffffffffe, %xmm2, %xmm2 tion below elides several details that are important for per- 3 vcvttpd2dq %xmm2, %xmm3 formance (such as the use of vector instructions), and fo- 4 vpaddw B, %xmm3, %xmm3 cuses on functionality. The calling convention used by exp 5 vpsllq $0x14, %xmm3, %xmm3 includes storing the first argument and the return value of a 6 vpshufd $0x3, %xmm3, %xmm3 function in the register xmm0. We omit details about the x86 7 vmulpd C1, %xmm2, %xmm1 8 vaddpd %xmm1, %xmm0, %xmm1 syntax and describe the implementation at a high level. The 9 vmovapd T1, %xmm0 code is divided into several blocks by the horizontal lines in 10 vlddqu T8, %xmm2 Figure 1 and the instructions within a block compute a value 11 vmulpd %xmm1, %xmm2, %xmm2 of interest. 12 vaddpd T7, %xmm2, %xmm2 13 vmulpd %xmm1, %xmm2, %xmm2 • The first block (lines 1-3) computes N from the input x.
Load more

Recommended publications
  • ADSP-21065L SHARC User's Manual; Chapter 2, Computation
    &20387$7,2181,76 Figure 2-0. Table 2-0. Listing 2-0. The processor’s computation units provide the numeric processing power for performing DSP algorithms, performing operations on both fixed-point and floating-point numbers. Each computation unit executes instructions in a single cycle. The processor contains three computation units: • An arithmetic/logic unit (ALU) Performs a standard set of arithmetic and logic operations in both fixed-point and floating-point formats. • A multiplier Performs floating-point and fixed-point multiplication as well as fixed-point dual multiply/add or multiply/subtract operations. •A shifter Performs logical and arithmetic shifts, bit manipulation, field deposit and extraction operations on 32-bit operands and can derive exponents as well. ADSP-21065L SHARC User’s Manual 2-1 PM Data Bus DM Data Bus Register File Multiplier Shifter ALU 16 × 40-bit MR2 MR1 MR0 Figure 2-1. Computation units block diagram The computation units are architecturally arranged in parallel, as shown in Figure 2-1. The output from any computation unit can be input to any computation unit on the next cycle. The computation units store input operands and results locally in a ten-port register file. The Register File is accessible to the processor’s pro- gram memory data (PMD) bus and its data memory data (DMD) bus. Both of these buses transfer data between the computation units and internal memory, external memory, or other parts of the processor. This chapter covers these topics: • Data formats • Register File data storage and transfers
    [Show full text]
  • Most Computer Instructions Can Be Classified Into Three Categories
    Introduction: Data Transfer and Manipulation Most computer instructions can be classified into three categories: 1) Data transfer, 2) Data manipulation, 3) Program control instructions » Data transfer instruction cause transfer of data from one location to another » Data manipulation performs arithmatic, logic and shift operations. » Program control instructions provide decision making capabilities and change the path taken by the program when executed in computer. Data Transfer Instruction Typical Data Transfer Instruction : LD » Load : transfer from memory to a processor register, usually an AC (memory read) ST » Store : transfer from a processor register into memory (memory write) MOV » Move : transfer from one register to another register XCH » Exchange : swap information between two registers or a register and a memory word IN/OUT » Input/Output : transfer data among processor registers and input/output device PUSH/POP » Push/Pop : transfer data between processor registers and a memory stack MODE ASSEMBLY REGISTER TRANSFER CONVENTION Direct Address LD ADR ACM[ADR] Indirect Address LD @ADR ACM[M[ADR]] Relative Address LD $ADR ACM[PC+ADR] Immediate Address LD #NBR ACNBR Index Address LD ADR(X) ACM[ADR+XR] Register LD R1 ACR1 Register Indirect LD (R1) ACM[R1] Autoincrement LD (R1)+ ACM[R1], R1R1+1 8 Addressing Mode for the LOAD Instruction Data Manipulation Instruction 1) Arithmetic, 2) Logical and bit manipulation, 3) Shift Instruction Arithmetic Instructions : NAME MNEMONIC Increment INC Decrement DEC Add ADD Subtract SUB Multiply
    [Show full text]
  • The Central Processor Unit
    Systems Architecture The Central Processing Unit The Central Processing Unit – p. 1/11 The Computer System Application High-level Language Operating System Assembly Language Machine level Microprogram Digital logic Hardware / Software Interface The Central Processing Unit – p. 2/11 CPU Structure External Memory MAR: Memory MBR: Memory Address Register Buffer Register Address Incrementer R15 / PC R11 R7 R3 R14 / LR R10 R6 R2 R13 / SP R9 R5 R1 R12 R8 R4 R0 User Registers Booth’s Multiplier Barrel IR Shifter Control Unit CPSR 32-Bit ALU The Central Processing Unit – p. 3/11 CPU Registers Internal Registers Condition Flags PC Program Counter C Carry IR Instruction Register Z Zero MAR Memory Address Register N Negative MBR Memory Buffer Register V Overflow CPSR Current Processor Status Register Internal Devices User Registers ALU Arithmetic Logic Unit Rn Register n CU Control Unit n = 0 . 15 M Memory Store SP Stack Pointer MMU Mem Management Unit LR Link Register Note that each CPU has a different set of User Registers The Central Processing Unit – p. 4/11 Current Process Status Register • Holds a number of status flags: N True if result of last operation is Negative Z True if result of last operation was Zero or equal C True if an unsigned borrow (Carry over) occurred Value of last bit shifted V True if a signed borrow (oVerflow) occurred • Current execution mode: User Normal “user” program execution mode System Privileged operating system tasks Some operations can only be preformed in a System mode The Central Processing Unit – p. 5/11 Register Transfer Language NAME Value of register or unit ← Transfer of data MAR ← PC x: Guard, only if x true hcci: MAR ← PC (field) Specific field of unit ALU(C) ← 1 (name), bit (n) or range (n:m) R0 ← MBR(0:7) Rn User Register n R0 ← MBR num Decimal number R0 ← 128 2_num Binary number R1 ← 2_0100 0001 0xnum Hexadecimal number R2 ← 0x40 M(addr) Memory Access (addr) MBR ← M(MAR) IR(field) Specified field of IR CU ← IR(op-code) ALU(field) Specified field of the ALU(C) ← 1 Arithmetic and Logic Unit The Central Processing Unit – p.
    [Show full text]
  • X86 Intrinsics Cheat Sheet Jan Finis [email protected]
    x86 Intrinsics Cheat Sheet Jan Finis [email protected] Bit Operations Conversions Boolean Logic Bit Shifting & Rotation Packed Conversions Convert all elements in a packed SSE register Reinterpet Casts Rounding Arithmetic Logic Shift Convert Float See also: Conversion to int Rotate Left/ Pack With S/D/I32 performs rounding implicitly Bool XOR Bool AND Bool NOT AND Bool OR Right Sign Extend Zero Extend 128bit Cast Shift Right Left/Right ≤64 16bit ↔ 32bit Saturation Conversion 128 SSE SSE SSE SSE Round up SSE2 xor SSE2 and SSE2 andnot SSE2 or SSE2 sra[i] SSE2 sl/rl[i] x86 _[l]rot[w]l/r CVT16 cvtX_Y SSE4.1 cvtX_Y SSE4.1 cvtX_Y SSE2 castX_Y si128,ps[SSE],pd si128,ps[SSE],pd si128,ps[SSE],pd si128,ps[SSE],pd epi16-64 epi16-64 (u16-64) ph ↔ ps SSE2 pack[u]s epi8-32 epu8-32 → epi8-32 SSE2 cvt[t]X_Y si128,ps/d (ceiling) mi xor_si128(mi a,mi b) mi and_si128(mi a,mi b) mi andnot_si128(mi a,mi b) mi or_si128(mi a,mi b) NOTE: Shifts elements right NOTE: Shifts elements left/ NOTE: Rotates bits in a left/ NOTE: Converts between 4x epi16,epi32 NOTE: Sign extends each NOTE: Zero extends each epi32,ps/d NOTE: Reinterpret casts !a & b while shifting in sign bits. right while shifting in zeros. right by a number of bits 16 bit floats and 4x 32 bit element from X to Y. Y must element from X to Y. Y must from X to Y. No operation is SSE4.1 ceil NOTE: Packs ints from two NOTE: Converts packed generated.
    [Show full text]
  • Bit Manipulation
    jhtp_appK_BitManipulation.fm Page 1 Tuesday, April 11, 2017 12:28 PM K Bit Manipulation K.1 Introduction This appendix presents an extensive discussion of bit-manipulation operators, followed by a discussion of class BitSet, which enables the creation of bit-array-like objects for setting and getting individual bit values. Java provides extensive bit-manipulation capabilities for programmers who need to get down to the “bits-and-bytes” level. Operating systems, test equipment software, networking software and many other kinds of software require that the programmer communicate “directly with the hardware.” We now discuss Java’s bit- manipulation capabilities and bitwise operators. K.2 Bit Manipulation and the Bitwise Operators Computers represent all data internally as sequences of bits. Each bit can assume the value 0 or the value 1. On most systems, a sequence of eight bits forms a byte—the standard storage unit for a variable of type byte. Other types are stored in larger numbers of bytes. The bitwise operators can manipulate the bits of integral operands (i.e., operations of type byte, char, short, int and long), but not floating-point operands. The discussions of bit- wise operators in this section show the binary representations of the integer operands. The bitwise operators are bitwise AND (&), bitwise inclusive OR (|), bitwise exclu- sive OR (^), left shift (<<), signed right shift (>>), unsigned right shift (>>>) and bitwise complement (~). The bitwise AND, bitwise inclusive OR and bitwise exclusive OR oper- ators compare their two operands bit by bit. The bitwise AND operator sets each bit in the result to 1 if and only if the corresponding bit in both operands is 1.
    [Show full text]
  • Bit-Level Transformation and Optimization for Hardware
    Bit-Level Transformation and Optimization for Hardware Synthesis of Algorithmic Descriptions Jiyu Zhang*† , Zhiru Zhang+, Sheng Zhou+, Mingxing Tan*, Xianhua Liu*, Xu Cheng*, Jason Cong† *MicroProcessor Research and Development Center, Peking University, Beijing, PRC † Computer Science Department, University Of California, Los Angeles, CA 90095, USA +AutoESL Design Technologies, Los Angeles, CA 90064, USA {zhangjiyu, tanmingxing, liuxianhua, chengxu}@mprc.pku.edu.cn {zhiruz, zhousheng}@autoesl.com, [email protected] ABSTRACT and more popularity [3-6]. However, high-quality As the complexity of integrated circuit systems implementations are difficult to achieve automatically, increases, automated hardware design from higher- especially when the description of the functionality is level abstraction is becoming more and more important. written in a high-level software programming language. However, for many high-level programming languages, For bitwise computation-intensive applications, one of such as C/C++, the description of bitwise access and the main difficulties is the lack of bit-accurate computation is not as direct as hardware description descriptions in high-level software programming languages, and hardware synthesis of algorithmic languages. The wide use of bitwise operations in descriptions may generate sub-optimal implement- certain application domains calls for specific bit-level tations for bitwise computation-intensive applications. transformation and optimization to assist hardware In this paper we introduce a bit-level
    [Show full text]
  • On the Standardization of Fundamental Bit Manipulation Utilities
    Document number: P0237R0 Date: 2016–02–12 Project: ISO JTC1/SC22/WG21: Programming Language C++ Audience: Library Evolution Working Group, SG14 Reply to: Vincent Reverdy ([email protected]) On the standardization of fundamental bit manipulation utilities Vincent Reverdy1 and Robert J. Brunner1 1Department of Astronomy, University of Illinois at Urbana-Champaign, 1002 W. Green St., Urbana, IL 61801 Abstract We discuss the addition to the standard library of class templates to ease the manipulation of bits in C++. This includes a bit_value class emulating a single bit, a bit_reference em- ulating a reference to a bit, a bit_pointer emulating a pointer to a bit, and a bit_iterator to iterate on bits. These tools would provide a solid foundation of algorithms operating on bits and would facilitate the use of unsigned integers as bit containers. Contents 1 Introduction2 2 Motivation2 3 Impact on the standard3 4 Design decisions4 5 Technical specications 16 6 Alternative technical specications 26 7 Discussion and open questions 29 8 Acknowledgements 30 9 References 31 1 1 Introduction This proposal introduces a class template std::bit_reference that is designed to emulate a ref- erence to a bit. It is inspired by the existing nested classes of the standard library: std::bitset:: reference and std::vector<bool>::reference, but this new class is made available to C++ developers as a basic tool to construct their own bit containers and algorithms. It is supple- mented by a std::bit_value class to deal with non-referenced and temporary bit values. To provide a complete and consistent set of tools, we also introduce a std::bit_pointer in order to emulate the behaviour of a pointer to a bit.
    [Show full text]
  • Bit Manipulation.Pptx
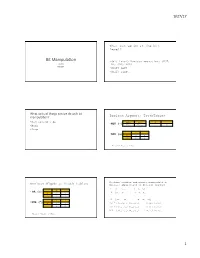
    9/27/17 What can we do at the bit level? Bit Manipula+on • (bit level) Boolean operations (NOT, CS 203 OR, AND, XOR) Fall 2017 • Shift left • Shift right 1 2 What sorts of things can we do with bit manipula+on? Boolean Algebra: TruthTables • Multiply/divide False True 0 1 • NOT (~) • Mask True False 1 0 • Swap • 0 1 AND (&) 0 0 0 1 0 1 Where: 0 = False; 1 = True 3 4 Boolean algebra and binary manipulation: Boolean Algebra: Truth Tables Bitwise application of Boolean algebra X = [xn-1 xn-2 … x2 x1 x0] 0 1 • OR (|) Y = [y y … y y y ] 0 0 1 n-1 n-2 2 1 0 ---------------------------------------------------------- 1 1 1 ~X = [~x ~x … ~x ~x ~x ] 0 1 n-1 n-2 2 1 0 • XOR (^) 0 0 1 X&Y = [(xn-1&yn-1) (xn-2&yn-2) … (x1&y1) (x0&y0)] 1 1 0 X|Y = [(xn-1|yn-1) (xn-2|yn-2) … (x1|y1) (x0|y0)] X^Y = [(xn-1^yn-1) (xn-2^yn-2) … (x1^y1) (x0^y0)] Where: 0 = False; 1 = True 5 6 1 9/27/17 Boolean algebra and binary manipulation: Boolean algebra and binary manipulation: Bitwise application of Boolean algebra Bitwise application of Boolean algebra • Given X = [00101111]; Y = [10111000] • Given X = [00101111];Y = [10111000] • ~X = ? • X&Y = ? • ~X = [11010000] X&Y = [00101000] • X|Y = ? • X^Y = ? • X|Y =[10111111] X^Y = [10010111] 7 8 Subtracting by adding: 2’s Using 2’s complement to complement subtract by adding • X – Y = X + (-Y) make use of this fact!!! • 5 – 3 • 1’s complement --- flip the bits [00000101] – [00000011] • 2’s complement of a number is the 1’s complement + 1 = [00000101] + 2’s complement ([00000011]) = [00000101] + ([11111100] + [00000001]) [00000000] = [00000101] + [11111101] 1’s complement [11111111] = [00000010] = 2 2’s complement [00000000] 10 When using 2’s complement, do not have the 2- zero issue 9 10 What can we do?: What can we do?: XOR as a programmable inverter Masking • Given a bit a; how you set it determines whether • A series of bits (word, half-word, etc.) can act as a another bit b is inverted (flipped) or left mask unchanged.
    [Show full text]
  • 5 Combinatorial Components 5.0 Full Adder Full Subtractor
    5 Combinatorial Components Use for data transformation, manipulation, interconnection, and for control: • arithmetic operations - addition, subtraction, multiplication and division. • logic operations - AND, OR, XOR, and NOT. • comparison operations - greater than, equal to, and less than. • bit manipulation operations - shift, rotation, extraction, and insertion. • interconnect components - selectors, and buses - used to connect different components together. • conversion components - decoders and encoders - used for conversion between different codes. • universal components - ROMs and programmable-logic arrays (PLAs) - used primarily in the design of control units. 5.0 Full adder x y c c s i i i i+1 i i = xi' yi' ci + xi' yi ci' + xi yi' ci' + xi yi ci 00000 = (xi' yi + xi yi') ci ' + (xi' yi' + xi yi) ci 00101 = (xi ⊕ yi) ci' + (xi ~ yi) ci 01001 = (xi ⊕ yi) ⊕ ci 01110 10001 ci+1 = xi' yi ci + xi yi' ci + xi yi ci' + xi yi ci 10110 = xi yi (ci' + ci) + ci (xi' yi + xi yi') 11010 = xi yi • 1 + ci (xi ⊕ yi) 11111 xi yi XY c i+1 Cout FA Cin ci S si Circuit for Full Adder Full subtractor bin xybout d Comment 0000 0x-bin-y = d = 0-0 = 0 0 0 1 1 1 0-0-1 = borrow 2-1 = 1 0 1 0 0 1 1-0-0=1 with no borrow 0 1 1 0 0 1-0-1=0 with no borrow 1001 1x=0-1=-1 because of bin=1, therefore, borrow 2-1=1. Finally, 1-0=1 1011 0x-bin-y=borrow 2-1-1=0 1 1 0 0 0 1-1-0=0 with no borrow 1111 1x-bin=1-1=0.
    [Show full text]
  • Performing Advanced Bit Manipulations Efficiently in General-Purpose Processors
    Performing Advanced Bit Manipulations Efficiently in General-Purpose Processors Yedidya Hilewitz and Ruby B. Lee Department of Electrical Engineering , Princeton University, Princeton, NJ 08544 USA {hilewitz, rblee}@princeton.edu Abstract processors also have Extract_field and Deposit_field operations, which can be viewed as variants of This paper describes a new basis for the Shift_Right and Shift_Left operations, with certain implementation of a shifter functional unit. We present bits masked out and set to zeros or replicated-sign bits. a design based on the inverse butterfly and butterfly There are many emerging applications, such as datapath circuits that performs the standard shift and cryptography, imaging and biometrics, where more rotate operations, as well as more advanced extract, advanced bit manipulation operations are needed. deposit and mix operations found in some processors. While these can be built from the simpler logical and Additionally, it also supports important new classes of shift operations, the applications using these advanced even more advanced bit manipulation instructions bit manipulation operations are significantly sped up if recently proposed: these include arbitrary bit the processor can support more powerful bit permutations, bit scatter and bit gather instructions. manipulation instructions. Such operations include The new functional unit’s datapath is comparable in arbitrary bit permutations, performing multiple bit- latency to that of the classic barrel shifter. It replaces field extract operations in parallel, and performing two existing functional units - shifter and mix - with a multiple bit-field deposit operations in parallel. We much more powerful one. call these permutation (perm), parallel extract (pex) or Keywords: shifter, rotations, permutations, bit bit gather, and parallel deposit (pdep) or bit scatter manipulations, arithmetic, processor operations, respectively.
    [Show full text]
  • SH7269 CPU Board R0K57269 Installation Manual
    User’s Manual User’s SH7269 CPU Board 32 R0K572690C000BR Installation Manual Renesas 32-Bit RISC Microcomputer SuperHTM RISC engine Family/SH7260 Series All information contained in these materials, including products and product specifications, represents information on the product at the time of publication and is subject to change by Renesas Electronics Corporation without notice. Please review the latest information published by Renesas Electronics Corporation through various means, including the Renesas Electronics Corporation website (http://www.renesas.com). www.renesas.com Rev.1.00 2011.12 Notice 1. All information included in this document is current as of the date this document is issued. Such information, however, is subject to change without any prior notice. Before purchasing or using any Renesas Electronics products listed herein, please confirm the latest product information with a Renesas Electronics sales office. Also, please pay regular and careful attention to additional and different information to be disclosed by Renesas Electronics such as that disclosed through our website. 2. Renesas Electronics does not assume any liability for infringement of patents, copyrights, or other intellectual property rights of third parties by or arising from the use of Renesas Electronics products or technical information described in this document. No license, express, implied or otherwise, is granted hereby under any patents, copyrights or other intellectual property rights of Renesas Electronics or others. 3. You should not alter, modify, copy, or otherwise misappropriate any Renesas Electronics product, whether in whole or in part. 4. Descriptions of circuits, software and other related information in this document are provided only to illustrate the operation of semiconductor products and application examples.
    [Show full text]
  • SH-4A Software Manual
    REJ09B0003-0150Z SH-4A 32 Software Manual Renesas 32-Bit RISC Microcomputer SuperH™ RISC engine Family Rev.1.50 Revision Date: Oct. 29, 2004 Rev. 1.50, 10/04, page ii of xx Keep safety first in your circuit designs! 1. Renesas Technology Corp. puts the maximum effort into making semiconductor products better and more reliable, but there is always the possibility that trouble may occur with them. Trouble with semiconductors may lead to personal injury, fire or property damage. Remember to give due consideration to safety when making your circuit designs, with appropriate measures such as (i) placement of substitutive, auxiliary circuits, (ii) use of nonflammable material or (iii) prevention against any malfunction or mishap. Notes regarding these materials 1. These materials are intended as a reference to assist our customers in the selection of the Renesas Technology Corp. product best suited to the customer's application; they do not convey any license under any intellectual property rights, or any other rights, belonging to Renesas Technology Corp. or a third party. 2. Renesas Technology Corp. assumes no responsibility for any damage, or infringement of any third- party's rights, originating in the use of any product data, diagrams, charts, programs, algorithms, or circuit application examples contained in these materials. 3. All information contained in these materials, including product data, diagrams, charts, programs and algorithms represents information on products at the time of publication of these materials, and are subject to change by Renesas Technology Corp. without notice due to product improvements or other reasons. It is therefore recommended that customers contact Renesas Technology Corp.
    [Show full text]