DOCSLIB.ORG

Equivalent Series Resistnace

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Equivalent Series Resistnace 1 Engineering Bulletins Capacitors 1. Equivalent Series Resistance (ESR) . 2 2. Charging Capacitors: Polarization and Leakage Currents . 10 3. Metallized Electrode Capacitors for Pulsed Power Applications . 21 1 Equivalent Series Resistance (ESR) Many electrical engineers are General Atomics Energy Prod- familiar with a circuit model (Figure 1) ucts (GAEP) has attempted to avoid in- of a non-ideal capacitor which includes correct application of ESR information a series inductance (the ESL) and a se- by not listing an ESR value in its stan- ries resistance (the ESR). This model dard product sales literature. Each cus- is very misleading because it often re- tomer who is concerned about this pa- sults in the assumption that the equiva- rameter is asked how the ESR value is lent resistance is actually a true resis- to be used in his or her calculations or tance, having essentially constant value models. This allows us to tailor a mea- over a wide range of conditions [7]. In surement method to the requirements of truth, the Equivalent Series Resistance a particular application. Although this is the value of resistance which is equal is more complex and time-consuming, to the total effect of a large and com- it is the only way of assuring that the plex set of energy loss mechanisms quoted ESR values have real mean- occuring under a particular set of ing for the intended purpose. measurement or operating conditions. Capacitor manufacturers often define the ESR as the impedance mea- CS LS RS sured at the resonant frequency of the (ESL) (ESR) capacitor, or the value of the ESR at a V particular AC frequency (e.g. 100 kHz), usually measured with a bridge, LCR meter, or impedance analyzer at about I 1 V. These are definitions which make δ ωCS it easy to measure the ESR but may be θ inadequate to describe the behavior of a high voltage capacitor under actual RSI operating conditions. Figure 1. AC voltage signal applied to circuit below resonant frequency. 2 In this Technical Note, we in- energy stored over all frequencies (con- tend to briefly describe why the ESR stant DF), the ESR decreases with in- does not behave like a simple resistance creasing frequency, as can be seen by as the result of the physics of a capaci- rearranging equation (1): tor. We will then examine several meth- ods of measuring the ESR and how the ESR = DF/ωC ~ 1/ω (2) exact test conditions affect the results of each. Finally, we will discuss how Figure 2 illustrates the hypo- ESR values are often used and suggest thetical constant-DF case. how to specify the ESR and the proper C = 1 µF measurement technique for your appli- DF = Constant = 0.001 cation. 1.6 1.4 Capacitor Physics 1.2 and ESR 1.0 Dielectric Loss 0.8 Metal Loss If we apply an AC voltage sig- Both nal to the circuit of Figure 1 at a fre- ESR (Ohms) 0.6 quency well below the resonant fre- 0.4 quency, we observe a phase shift be- 0.2 tween voltage and current which is less than 90 degrees. The difference be- 0.0 tween the phase angle and 90 degrees is 246810 the defect angle (δ), which can be used Log (Frequency, HZ) to determine the effective resistive im- pedance using: Figure 2. Hypothetical constant/DF case. tangent (δ) = Zr/Zc . C = 1 µF = ESR ω C (1) DF (dielectrric) = 0.001 R (metal) = 0.00001Ω .00002 where Zr and Zc are the resistive and .00018 capacitive impedances, ω is the angular frequency, and C is the capacitance. .00016 Note that tangent δ is the same as the .00014 Skin dissipation factor, or DF [4]. .00012 Effect .00010 The energy loss in the circuit is .00008 ESR (Ohms) ESR proportional to the power factor, PF, .00006 which is given by the cosine of the phase Total ESR Dielectric Loss .00004 Metal Loss angle. The DF is approximately the Both same as the PF for small values (e.g. DF .00002 < 0.1 or 10 %). .00000 24612 810 14 If we assume that the energy Log (Frequency, HZ) dissipated is a constant fraction of the Figure 3. ESR as a function of frequency. 3 The ESR of a 1 µF capacitor has The dielectric losses of a given been modelled assuming that the di- material can be described by its Dissi- electric losses result in a constant DF pation Factor (DF). If the dielectric loss of 0.001 or 0.1% and the ohmic resis- were the only loss mechanism operat- tance is 0.01 milliohm. The resulting ing in a capacitor, then the DF of the ESR is shown as a function of fre- capacitor would be independent of its quency in Figure 3. The ESR falls size and geometry and internal configu- from a value of 1.6 ohm at 100 Hz to ration. Capacitors of any size made with a value of 0.01 milliohm at 5 MHz. the same material would have the same Above this frequency the ESR is DF when measured under identical con- largely determined by the ohmic re- ditions. The ESR could then easily be sistance of the conductors, and re- computed using equation (2). However, mains relatively constant until the skin the capacitor DF and ESR do depend effect begins to reduce the effective on the electrodes and their configura- thickness of the foil electrodes. The tion, as described below. ESR then begins to increase in pro- portion to f 0.5 above about 30 MHz. Ferroelectric hysteresis losses are observed in certain high dielectric When examined more closely, constant materials, most notably ceram- the losses vary as a function of voltage, ics. These losses are a strong function temperature, and other aspects of the of applied voltage. This loss mechanism waveform. This is because there are a arises when the internal polarization variety of energy loss mechanisms field has the same order of magnitude which act within a capacitor. Some of as the applied field. Under these condi- these reside within the dielectric while tions the dielectric response saturates. others involve the conductors carrying Capacitors made with such materials the current. Below we describe some exhibit permanent polarization, variable of these mechanisms and the operating capacitance as a function of voltage, and parameters which strongly effect the extreme sensitivity to reversals of voltage. magnitude of the losses which are asso- ciated with them. Dielectric conduction losses are caused by the actual transport of Dielectric losses are usually the charge across the volume of the dielec- most important losses in a film capaci- tric or across internal dielectric inter- tor. These losses are associated with the faces. These losses are largest at low polarization and relaxation of the dielec- frequencies and higher temperatures. tric material in response to the applica- Because conduction in a dielectric ma- tion and removal of voltage from the terial can be strongly nonlinear (non- capacitor. As such, the magnitude of the Ohmic), conduction losses are often dielectric losses in a capacitor are, in strongly dependent on the voltage ap- general, both frequency and temperature plied to the capacitor. dependent. In this case, the largest losses occur at low temperatures or high Interfacial polarization losses frequencies, where dipole orientation is are closely related to dielectric conduc- most hindered. Dielectric losses (as tion. Many high voltage capacitors con- defined here) are not voltage-dependent. tain two or three different materials 4 within their dielectric systems – film within the metallic electrodes, the inter- and oil or paper, film and oil. Each nal wiring, and the terminals of the ca- material has different conduction prop- pacitor. (In electrolytic capacitors, erties and permittivity. As a result, the ohmic resistance in the electrolyte itself application of a DC voltage over a pe- represents the largest loss mechanism.) riod of time will result in a build-up of The resistance losses in the metal are conducted charge at the internal inter- quite constant as a function of tempera- faces between materials. This polariza- ture and frequency (until the skin depth tion of the dielectric is largely a low- in the electrodes becomes important, frequency phenomenon and the energy usually at several megahertz or higher). stored in this way is not available for Losses in the internal wiring and the ter- discharge at high frequency. Again, minal can be important in high current since the conduction is nonlinear, inter- applications, and should not be ignored. facial polarization will also generally be When high voltage capacitors are inter- nonlinearly voltage dependent. nally configured as a series string of lower voltage capacitor windings or This loss mechanism can be es- units, the ohmic resistance within a pecially important in pulse discharge given container size increases at the applications, where the capacitor is square of the voltage (or as the number charged over a relatively long period of of series elements). time and then discharged much more rapidly. Sparking between conductors or different points on the same conduc- Partial discharge losses can tor during the discharge has been re- occur within gas-filled or defective solid ported to occur in pulse capacitors [3]. capacitors or even in liquid-filled ca- For example, capacitors manufactured pacitors at high voltages. It is also com- with an inserted tab connection to the mon to have external corona on capaci- electrode foil which is only a pressure tor terminals (which can be considered contact have been found to exhibit a capacitor energy loss mechanism). points of localized melting after pulse Partial discharges are most energetic at discharge operation resulting from high rates of change of voltage (high dV/ sparks between the adjacent metallic dt), such as during a capacitor pulse dis- surfaces [3].
Load more

Recommended publications
  • Uprating of Electrolytic Capacitors
    White Paper Uprating of Electrolytic Capacitors By Joelle Arnold Uprating of Electrolytic Capacitors Aluminum electrolytic capacitors are comprised of two aluminum foils, a cathode and an anode, rolled together with an electrolyte-soaked paper spacer in between. An oxide film is grown on the anode to create the dielectric. Aluminum electrolytic capacitors are primarily used to filter low-frequency electrical signals, primarily in power designs. The critical functional parameters for aluminum electrolytic capacitors are defined as capacitance (C), leakage current (LC), equivalent series resistance (ESR), impedance (Z), and dissipation factor (DF). These five parameters are interrelated through the following schematic. Physically, leakage current (LC) tends to be primarily driven by the behavior of the dielectric. ESR is primarily driven by the behavior of the electrolyte. Physically, impedance (Z) is a summation of all the resistances throughout the capacitor, including resistances due to packaging. Electrically, Z is the summation of ESR and either the capacitive reactance (XC), at low frequency, or the inductance (LESL), at high frequency (see Figure 1). Dissipation factor is the ratio of ESR over XC. Therefore, a low ESR tends to give a low impedance and a low dissipation factor. 1.1 Functional Parameters (Specified in Datasheet) The functional parameters that can be provided in manufacturers’ datasheets are listed below 1.1.1 Capacitance vs. Temperature It can be seen that the manufacturer’s guarantee of ±20% stability of the capacitance is only relevant at room temperature. While a source of potential concern when operating aluminum electrolytic capacitors over an extended temperature range, previous research has demonstrated that the capacitance of this capacitor is extremely stable as a function of temperature (see Figure 2 and Figure 4).
    [Show full text]
  • Equivalent Series Resistance (ESR) of Capacitors
    Application Note 1 of 5 Equivalent Series Resistance (ESR) of Capacitors Questions continually arise concerning the correct definition of the ESR (Equivalent Series Resistance) of a capacitor and, more particularly, the difference between ESR and the actual physical series resistance (which we'll call Ras), the ohmic resistance of the leads and plates or foils. The definition and application of the term ESR has often been misconstrued. We hope this note will answer any questions and clarify any confusion that might exist. Very briefly, ESR is a measure of the total lossiness of a capacitor. It is larger than Ras because the actual series resistance is only one source of the total loss (usually a small part). The Series Equivalent Circuit At one frequency, a measurement of complex impedance gives two numbers, the real part and the imaginary part: Z = Rs + jXs. At that frequency, the impedance behaves like a series combination of an ideal resistance Rs and an ideal reactance Xs (Figure 1). Rs RS XS CS Figure 1: Equivalent series circuit representation If Xs is negative, the impedance is capacitive, and the general reactance can be replaced with a capacitance of: −1 Cs = ωXs We now have an equivalent circuit that is correct only at the measurement frequency. The resistance of this equivalent circuit is the equivalent series resistance ESR = Rs = Real part of Z © IET LABS, Inc., September 2019 Printed in U.S.A 035002 Rev. A4 1 of 5 Application Note 2 of 5 Add the dissipation FACTOR energy lost Real part of Z If we define the dissipation factor D as D = = energy stored (− Imaginary part of Z) Rs Then D = =Rsω C = (ESR) ω C (− )Xs If one took a pure resistance and a pure capacitance and connected them in series, then one could say that the ESR of the combination was indeed equal to the actual series resistance.
    [Show full text]
  • Application Note: ESR Losses in Ceramic Capacitors by Richard Fiore, Director of RF Applications Engineering American Technical Ceramics
    Application Note: ESR Losses In Ceramic Capacitors by Richard Fiore, Director of RF Applications Engineering American Technical Ceramics AMERICAN TECHNICAL CERAMICS ATC North America ATC Europe ATC Asia [email protected] [email protected] [email protected] www.atceramics.com ATC 001-923 Rev. D; 4/07 ESR LOSSES IN CERAMIC CAPACITORS In the world of RF ceramic chip capacitors, Equivalent Series Resistance (ESR) is often considered to be the single most important parameter in selecting the product to fit the application. ESR, typically expressed in milliohms, is the summation of all losses resulting from dielectric (Rsd) and metal elements (Rsm) of the capacitor, (ESR = Rsd+Rsm). Assessing how these losses affect circuit performance is essential when utilizing ceramic capacitors in virtually all RF designs. Advantage of Low Loss RF Capacitors Ceramics capacitors utilized in MRI imaging coils must exhibit Selecting low loss (ultra low ESR) chip capacitors is an important ultra low loss. These capacitors are used in conjunction with an consideration for virtually all RF circuit designs. Some examples of MRI coil in a tuned circuit configuration. Since the signals being the advantages are listed below for several application types. detected by an MRI scanner are extremely small, the losses of the Extended battery life is possible when using low loss capacitors in coil circuit must be kept very low, usually in the order of a few applications such as source bypassing and drain coupling in the milliohms. Excessive ESR losses will degrade the resolution of the final power amplifier stage of a handheld portable transmitter image unless steps are taken to reduce these losses.
    [Show full text]
  • LOSSY CAPACITORS 1 Dielectric Loss
    Chapter 3—Lossy Capacitors 3–1 LOSSY CAPACITORS 1 Dielectric Loss Capacitors are used for a wide variety of purposes and are made of many different materials in many different styles. For purposes of discussion we will consider three broad types, that is, capacitors made for ac, dc, and pulse applications. The ac case is the most general since ac capacitors will work (or at least survive) in dc and pulse applications, where the reverse may not be true. It is important to consider the losses in ac capacitors. All dielectrics (except vacuum) have two types of losses. One is a conduction loss, representing the flow of actual charge through the dielectric. The other is a dielectric loss due to movement or rotation of the atoms or molecules in an alternating electric field. Dielectric losses in water are the reason for food and drink getting hot in a microwave oven. One way of describing dielectric losses is to consider the permittivity as a complex number, defined as = − j = ||e−jδ (1) where = ac capacitivity = dielectric loss factor δ = dielectric loss angle Capacitance is a complex number C∗ in this definition, becoming the expected real number C as the losses go to zero. That is, we define C∗ = C − jC (2) One reason for defining a complex capacitance is that we can use the complex value in any equation derived for a real capacitance in a sinusoidal application, and get the correct phase shifts and power losses by applying the usual rules of circuit theory. This means that most of our analyses are already done, and we do not need to start over just because we now have a lossy capacitor.
    [Show full text]
  • Electrical and Capacitive Methods for Detecting Degradation in Wire Insulation Robert Thomas Sheldon Iowa State University
    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2012 Electrical and capacitive methods for detecting degradation in wire insulation Robert Thomas Sheldon Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Electrical and Electronics Commons, and the Mechanics of Materials Commons Recommended Citation Sheldon, Robert Thomas, "Electrical and capacitive methods for detecting degradation in wire insulation" (2012). Graduate Theses and Dissertations. 12681. https://lib.dr.iastate.edu/etd/12681 This Thesis is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Electrical and capacitive methods for detecting degradation in wire insulation by Robert T. Sheldon A thesis submitted to the graduate faculty in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Major: Electrical Engineering Program of Study Committee: Nicola Bowler, Major Professor Brian K. Hornbuckle Jiming Song Iowa State University Ames, Iowa 2012 Copyright c Robert T. Sheldon, 2012. All rights reserved. ii To my parents, Kevin and Victoria, and my sister, Laura, for their neverending love and support. iii TABLE OF CONTENTS LIST OF TABLES . vi LIST OF FIGURES . vii ABSTRACT . xii CHAPTER 1. GENERAL INTRODUCTION . 1 1.1 Introduction . .1 1.2 Literature survey . .1 1.2.1 Extant methods of insulation characterization . .1 1.2.2 Capacitive sensing .
    [Show full text]
  • Dielectric Loss and Ferroelectric Hysteresis
    SEPTEMBER 2018 I SS U E #117 TECHNICALTIDBITS MATERION PERFORMANCE ALLOYS DIELECTRIC LOSS AND FERROELECTRIC HYSTERESIS Last month we made the observation that the per- The amount of energy converted to heat during a polar- mittivity of an ideal capacitor is equal to the relative ization cycle is known as the dissipation factor (Df), permittivity (dielectric constant, abbreviated loss tangent or tan ( ), with being the loss angle. Dk or r) multiplied by the permittivity constant The derivation of the loss angle and the tangent thereof δ δ At a Loss! – A brief ( 0). This is true for direct current (DC) conditions, or can be a bit esoteric unless you are an electrical engi- ε discussion on energy lost for ideal, lossless dielectric materials. However, nature neer. Technical Tidbits always tries to strike a balance rarelyε presents us with ideal materials or conditions, between oversimplification (with a risk of inaccuracy) as waste heat in materials so we have to consider real-world cases. and getting too in depth for introductory material due to the presence of (getting lost in the weeds). However, if you are comfort- changing electric fields. As discussed last month, under the influence of an able with phasors as well as real and imaginary parts of externally applied electric field, the electric dipoles current and capacitance, then feel free to research on. in a polarizable material will align themselves with the field, if they are free to rotate or move, and if they Under AC conditions, all realistic dielectric materials will have enough time to do so. Of course, such movement have losses.
    [Show full text]
  • The Effects of Piezoelectric Ceramic Dissipation Factor on the Performance of Ultrasonic Transducers
    The Effects of Piezoelectric Ceramic Dissipation Factor on the Performance of Ultrasonic Transducers Dominick A. DeAngelis and Gary W. Schulze 7 Dies Transducer Tool Device Forming Gas Wand for Cu Ball Bonded Stacked Die Device (SEM) Wire Bonding in Action with Fine Copper Wire (20 Wires/Sec) COPPER OR GOLD WIRE Kulicke & Soffa’s Flagship Capillary Semiconductor Tool Wire Bonding Machine Ultrasonic Transducer Used For Wire Bonding Machine Primary steps of the Wire Bond Cycle 41 th UIA Symposium, San Francisco, CA, USA 18-Apr-12 -1- OUTLINE Specific Application and Definition of Dissipation Factor ( DF ) How Does DF Affect Transducer Performance? Ball After EFO Research Summary Equivalent Circuit Model for DF Measuring DF Model Parameters Measuring Porosity of Piezo Ceramics Mixing Rules for Piezo Properties FEA Modeling and Experimental Results Conclusions Questions? 41 th UIA Symposium, San Francisco, CA, USA 18-Apr-12 -2- SPECIFIC TRANSDUCER APPLICATION K&S is the leading MFG of semiconductor wire bonding equipment Transducer delivers energy to a capillary tool for welding tiny wires Patented single piece “Unibody” design is ideal for research studies Portability across 100’s of machines required for same customer device Piezo Stack Transducer Transducer Specs Body On IConn Machine 500 mA Max Current 50/120 kHz Operating Modes Transducer 80 Ohm Max Impedance 1¢ US Operation 40 Bonds/Sec Capillary Device Bond Duration ~10 mSec PZT8 Ceramics (4X) New IConn Capillary Transducer Tool EFO (Spark) Diced Parts (thk=1mm) 1¢ US
    [Show full text]
  • Cornell Dubilier – Aluminum Electrolytic Capacitor Application
    Aluminum Electrolytic Capacitor Application Guide This guide is a full handbook on aluminum electrolytic capacitors, of course with emphasis on Cornell Dubilier’s types. It covers construction in depth and discloses the latest information on performance and application for the major aluminum electrolytic types made worldwide. We encourage you to tell us what more you’d like to know, so we can improve this guide. CONTENTS PAGE Capacitor Construction 2 Other Types of Capacitors Comparison 4 Characterization and Circuit Model 5 TABLES PAGE Temperature Range 6 Capacitor Parameter Formulas 6 Capacitance 7 Base Lives and Max Core Temperatures 14 Dissipation Factor (DF) 7 Thermal Resistance Screw Terminal Capacitors 17 Equivalent Series Resistance (ESR) 8 Thermal Resistance for Snap-in Capacitors 19 Impedance (Z) 8 Pressure Relief Device Clearance 21 Low-Temperature Impedance 8 Screw Tightening Torque for Screw Terminals 21 DC Leakage Current (DCL) 8 Maximum Currents for Screw Terminals 21 Voltage Withstanding 9 Tightening Torque for Nylon Mounting Nuts 22 Ripple Current 10 Inductance 10 Self-Resonant Frequency 10 Dielectric Absorption 11 Insulation and Grounding 11 Elevation & External Pressure 11 Vibration Withstanding Capability 11 Safety Considerations 11 Capacitor Bank Configurations 12 Non-Polar and Motor Start Capacitors 13 Reliability and Lifetime 13 Cooling and Thermal Resistance 16 Process Considerations 19 Mounting 20 Disposal of Capacitors 22 ALUMINUM ELECTROLYTIC CAPACITOR OVERVIEW electrolyte. The positive plate is the anode foil; the dielectric is the insulating aluminum oxide on the anode foil; the true negative Except for a few surface-mount technology (SMT) aluminum plate is the conductive, liquid electrolyte, and the cathode foil electrolytic capacitor types with solid electrolyte systems, an connects to the electrolyte.
    [Show full text]
  • The Proper Usage Method of Conductive Polymer Solid Aluminum Electrolytic Capacitor
    The Proper Usage Method of Conductive Polymer Solid Aluminum Electrolytic Capacitor Ⅰ.Lifetime Estimation Subject series：FR/FH/FG/FF/FS/FL/FT/FP/VB/VP/VS Conductive polymer aluminum solid capacitors are finite life electronic components like aluminum electrolytic capacitors. The lifetime is affected by ambient temperature, humidity, ripple current and surge voltage. The lifetime of aluminum electrolytic capacitors is affected mainly by the loss of electrolyte as the result of the liquid electrolyte evaporating through the rubber seal materials, resulting in capacitance drop and tanδ rise.On the other hand, the lifetime of conductive polymer aluminum solid capacitors is affected mainly by oxidation degradation of the conductive polymer caused by osmose of oxygen or the thermal degradation of the conductive polymer by ambient temperature or self-heating, resulting in ESR rise and tanδ rise.The infiltration rate of the oxygen is depend on the temperature as the liquid electrolyte evaporation and the relationship follows the Arrhenius's Law, too. Similarly, thermal degradation of the conductive polymer by self-heating follows the Arrhenius's Law, too.Therefore, the lifetime estimation has been using the ℃ theory of lifetime increasing by 10 times at every 20 reducing of the ambient temperature. 1. Lifetime Estimation Equation (1) can be used for estimating the lifetime of the conductive polymer aluminum solid capacitors based on the ambient temperature and the rise of internal temperature due to ripple current. (T0-TX)/20 LX=L0X10 -----------------------------------------------(1) Lx：Estimation of actual lifetime (hour) Lo：Specified lifetime with the rated voltage at the upper limit of the category temperature (hour) To：Maximum category temperature (℃) Tx：Actual ambient temperature of the capacitor (℃) Longer lifetime is expected by lowering the ripple current and the ambient temperature.
    [Show full text]
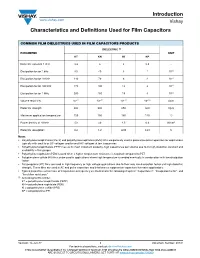
  • Introduction Characteristics and Definitions Used for Film Capacitors
    Introduction www.vishay.com Vishay Characteristics and Definitions Used for Film Capacitors COMMON FILM DIELECTRICS USED IN FILM CAPACITORS PRODUCTS DIELECTRIC (1) PARAMETER UNIT KT KN KI KP Dielectric constant 1 kHz 3.3 3 3 2.2 - Dissipation factor 1 kHz 50 40 3 1 10-4 Dissipation factor 10 kHz 110 70 6 2 10-4 Dissipation factor 100 kHz 170 100 12 2 10-4 Dissipation factor 1 MHz 200 150 18 4 10-4 Volume resistivity 10+17 10+17 10+17 10+18 Ωcm Dielectric strength 400 300 250 600 V/μm Maximum application temperature 125 150 160 110 °C Power density at 10 kHz 50 40 2.5 0.6 W/cm3 Dielectric absorption 0.2 1.2 0.05 0.01 % Notes • Polyethylene terephthalate (PETP) and polyethylene naphtalate (PEN) films are generally used in general purpose capacitors for applications typically with small bias DC voltages and/or small AC voltages at low frequencies • Polyethylene terephthalate (PETP) has as its most important property, high capacitance per volume due to its high dielectric constant and availability in thin gauges • Polyethylene naphtalate (PEN) is used when a higher temperature resistance is required compared to PET • Polyphenylene sulfide (KI) film can be used in applications where high temperature is needed eventually in combination with low dissipation factor • Polypropylene (KP) films are used in high frequency or high voltage applications due to their very low dissipation factor and high dielectric strength. These films are used in AC and pulse capacitors and interference suppression capacitors for mains applications • Typical properties as functions of temperature or frequency are illustrated in the following chapters: “Capacitance”, “Dissipation factor”, and “Insulation resistance” (1) According to IEC 60062: KT = polyethylene terephthalate (PETP) KN = polyethylene naphtalate (PEN) KI = polyphenylene sulfide (PPS) KP = polypropylene (PP) Revision: 14-Jun-17 1 Document Number: 28147 For technical questions, contact: [email protected] THIS DOCUMENT IS SUBJECT TO CHANGE WITHOUT NOTICE.
    [Show full text]
  • Dissipation Factor, Power Factor, and Relative Permittivity (Dielectric Constant)
    DISSIPATION FACTOR, POWER FACTOR, AND RELATIVE PERMITTIVITY (DIELECTRIC CONSTANT) By I.A.R. Gray Transformer Chemistry Services Background: There is a relationship between the dissipation factor, the power factor, and the permittivity or dielectric constant. They all relate to the dielectric losses in an insulating fluid when used in an alternating electric field. The permittivity is represented as a complex quantity in the following manner: e* = e' - j e" ; where e* is the complex permittivity, e' is the real or measured permittivity, and e" is the imaginary permittivity. In the presence of an alternating field there is created a capacitance current and a resistive current that are 90o out of phase with respect to each other. The vector sum of these two currents represents the total current and the angle between the capacitance current vector and the resultant total current vector is defined as the loss angle, d. The ratio of the imaginary to the real part of the permittivity is equal to tan d; i.e. tan d = e" / e'. The factor tan d is defined as the dissipation factor, D, and represents the dielectric loss in the insulating fluid. The power factor, P, is defined as sin d. The relationship between D and P is the following: D2 - F2 = D2 F2, thus if you know one value you can calculate the other. Furthermore for small values of d, tan d ~ sin d, thus for values of tan d up to 0.05 the power factor and the dissipation factor are the same within one part in a thousand.
    [Show full text]
  • Precision LCR Meter
    Precision LCR Meter LCR-800 USER MANUAL GW INSTEK PART NO. 82CR-81900MK1 This manual contains proprietary information, which is protected by copyright. All rights are reserved. No part of this manual may be photocopied, reproduced or translated to another language without prior written consent of the Good Will Instrument company. The information in this manual was correct at the time of printing. However, Good Will continues to improve products and reserves the right to change specifications, equipment, and maintenance procedures at any time without notice. ISO-9001 CERTIFIED MANUFACTURER Good Will Instrument Co., Ltd. No. 7-1, Jhongsing Rd., Tucheng City, Taipei County 236, Taiwan. SAFETY INSTRUCTIONS LCR-800 User Manual INTERACE ...................................................................... 111 RS232 Interface Configuration ........... 112 Table of Contents Signal Overview ................................. 116 SAFETY INSTRUCTIONS ................................................... 5 FAQ ............................................................................... 121 GETTING STARTED ......................................................... 10 APPENDIX ..................................................................... 123 Main Features ...................................... 11 Fuse Replacement .............................. 123 Measurement Type ............................... 12 Circuit Theory and Formula ................ 124 Front Panel Overview ........................... 13 Accuracy Definitions .........................
    [Show full text]