Statistics of the Environment?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Conjunction Fallacy' Revisited: How Intelligent Inferences Look Like Reasoning Errors
Journal of Behavioral Decision Making J. Behav. Dec. Making, 12: 275±305 (1999) The `Conjunction Fallacy' Revisited: How Intelligent Inferences Look Like Reasoning Errors RALPH HERTWIG* and GERD GIGERENZER Max Planck Institute for Human Development, Berlin, Germany ABSTRACT Findings in recent research on the `conjunction fallacy' have been taken as evid- ence that our minds are not designed to work by the rules of probability. This conclusion springs from the idea that norms should be content-blind Ð in the present case, the assumption that sound reasoning requires following the con- junction rule of probability theory. But content-blind norms overlook some of the intelligent ways in which humans deal with uncertainty, for instance, when drawing semantic and pragmatic inferences. In a series of studies, we ®rst show that people infer nonmathematical meanings of the polysemous term `probability' in the classic Linda conjunction problem. We then demonstrate that one can design contexts in which people infer mathematical meanings of the term and are therefore more likely to conform to the conjunction rule. Finally, we report evidence that the term `frequency' narrows the spectrum of possible interpreta- tions of `probability' down to its mathematical meanings, and that this fact Ð rather than the presence or absence of `extensional cues' Ð accounts for the low proportion of violations of the conjunction rule when people are asked for frequency judgments. We conclude that a failure to recognize the human capacity for semantic and pragmatic inference can lead rational responses to be misclassi®ed as fallacies. Copyright # 1999 John Wiley & Sons, Ltd. KEY WORDS conjunction fallacy; probabalistic thinking; frequentistic thinking; probability People's apparent failures to reason probabilistically in experimental contexts have raised serious concerns about our ability to reason rationally in real-world environments. -

Thinking About the Ultimate Argument for Realism∗
Thinking About the Ultimate Argument for Realism∗ Stathis Psillos Department of Philosophy and History of Science University of Athens Panepistimioupolis (University Campus) Athens 15771 Greece [email protected] 1. Introduction Alan Musgrave has been one of the most passionate defenders of scientific realism. Most of his papers in this area are, by now, classics. The title of my paper alludes to Musgrave’s piece “The Ultimate Argument for Realism”, though the expression is Bas van Fraassen’s (1980, 39), and the argument is Hilary Putnam’s (1975, 73): realism “is the only philosophy of science that does not make the success of science a miracle”. Hence, the code-name ‘no-miracles’ argument (henceforth, NMA). In fact, NMA has quite a history and a variety of formulations. I have documented all this in my (1999, chapter 4). But, no matter how exactly the argument is formulated, its thrust is that the success of scientific theories lends credence to the following two theses: a) that scientific theories should be interpreted realistically and b) that, so interpreted, these theories are approximately true. The original authors of the argument, however, did not put an extra stress on novel predictions, which, as Musgrave (1988) makes plain, is the litmus test for the ability of any approach to science to explain the success of science. Here is why reference to novel predictions is crucial. Realistically understood, theories entail too many novel claims, most of them about unobservables (e.g., that ∗ I want to dedicate this paper to Alan Musgrave. His exceptional combination of clear-headed and profound philosophical thinking has been a model for me. -

Graphical Techniques in Debiasing: an Exploratory Study
GRAPHICAL TECHNIQUES IN DEBIASING: AN EXPLORATORY STUDY by S. Bhasker Information Systems Department Leonard N. Stern School of Business New York University New York, New York 10006 and A. Kumaraswamy Management Department Leonard N. Stern School of Business New York University New York, NY 10006 October, 1990 Center for Research on Information Systems Information Systems Department Leonard N. Stern School of Business New York University Working Paper Series STERN IS-90-19 Forthcoming in the Proceedings of the 1991 Hawaii International Conference on System Sciences Center for Digital Economy Research Stem School of Business IVorking Paper IS-90-19 Center for Digital Economy Research Stem School of Business IVorking Paper IS-90-19 2 Abstract Base rate and conjunction fallacies are consistent biases that influence decision making involving probability judgments. We develop simple graphical techniques and test their eflcacy in correcting for these biases. Preliminary results suggest that graphical techniques help to overcome these biases and improve decision making. We examine the implications of incorporating these simple techniques in Executive Information Systems. Introduction Today, senior executives operate in highly uncertain environments. They have to collect, process and analyze a deluge of information - most of it ambiguous. But, their limited information acquiring and processing capabilities constrain them in this task [25]. Increasingly, executives rely on executive information/support systems for various purposes like strategic scanning of their business environments, internal monitoring of their businesses, analysis of data available from various internal and external sources, and communications [5,19,32]. However, executive information systems are, at best, support tools. Executives still rely on their mental or cognitive models of their businesses and environments and develop heuristics to simplify decision problems [10,16,25]. -

An Overview of Environmental Statistics
An Overview of Environmental Statistics Richard L. Smith Department of Statistics and Operations Research University of North Carolina Chapel Hill, N.C., U.S.A. Theme Day in Environmental Statistics 55th Session of ISI Sydney, April 6, 2005 http://www.stat.unc.edu/postscript/rs/isitutorial.pdf 1 Environmental Statistics is by now an extremely broad field, in- volving application of just about every technique of statistics. Examples: • Pollution in atmosphere and water systems • Effects of pollution on human health and ecosystems • Uncertainties in forecasting climate and weather • Dynamics of ecological time series • Environmental effects on the genome and many more. 2 Some common themes: • Most problems involve time series of observations, but also spatial sampling, often involving irregular grids • Design of a spatial sampling scheme or a monitor network is important • Often the greatest interest is in extremes, for example – Air pollution standards often defined by number of cross- ings of a high threshold – Concern over impacts of climate change often focussed on climate extremes. Hence, must be able to character- ize likely frequencies of extreme events in future climate scenarios • Use of numerical models — not viewed in competition, but how we can use statistics to improve the information derived from models 3 I have chosen here to focus on three topics that have applications across several of these areas: I. Spatial and spatio-temporal statistics • Interpolation of an air pollution or meteorological field • Comparing data measured on different spatial scales • Assessing time trends in data collected on a spatial net- work II. Network design • Choosing where to place the monitors to satisfy some optimality criterion related to prediction or estimation III. -

Zusammenfassung
Zusammenfassung Auf den folgenden beiden Seiten werden die zuvor detailliert darge- stellten 100 Fehler nochmals übersichtlich gruppiert und klassifiziert. Der kompakte Überblick soll Sie dabei unterstützen, die systemati- schen Fehler durch geeignete Maßnahmen möglichst zu verhindern beziehungsweise so zu reduzieren, dass sich keine allzu negativen Auswirkungen auf Ihr operatives Geschäft ergeben! Eine gezielte und strukturierte Auseinandersetzung mit den Fehler(kategorie)n kann Sie ganz allgemein dabei unterstützen, Ihr Unternehmen „resilienter“ und „antifragiler“ aufzustellen, das heißt, dass Sie von negativen Entwicklungen nicht sofort umgeworfen werden (können). Außerdem kann eine strukturierte Auseinander- setzung auch dabei helfen, sich für weitere, hier nicht explizit genannte – aber ähnliche – Fehler zu wappnen. © Springer Fachmedien Wiesbaden GmbH, ein Teil von Springer Nature 2019 402 C. Glaser, Risiko im Management, https://doi.org/10.1007/978-3-658-25835-1 403 Zusammenfassung Zu viele Zu wenig Nicht ausreichend Informationen Informationsgehalt Zeit zur Verfügung Deshalb beachten wir Deshalb füllen wir die Deshalb nehmen wir häufig typischerweise nur… Lücken mit… an, dass… Veränderungen Mustern und bekannten wir Recht haben Außergewöhnliches Geschichten wir das schaffen können Wiederholungen Allgemeinheiten und das Naheliegendste auch Bekanntes/Anekdoten Stereotypen das Beste ist Bestätigungen vereinfachten wir beenden sollten, was Wahrscheinlichkeiten und wir angefangen haben Zahlen unsere Optionen einfacheren -

Statistical Tips for Interpreting Scientific Claims
Research Skills Seminar Series 2019 CAHS Research Education Program Statistical Tips for Interpreting Scientific Claims Mark Jones Statistician, Telethon Kids Institute 18 October 2019 Research Skills Seminar Series | CAHS Research Education Program Department of Child Health Research | Child and Adolescent Health Service ResearchEducationProgram.org © CAHS Research Education Program, Department of Child Health Research, Child and Adolescent Health Service, WA 2019 Copyright to this material produced by the CAHS Research Education Program, Department of Child Health Research, Child and Adolescent Health Service, Western Australia, under the provisions of the Copyright Act 1968 (C’wth Australia). Apart from any fair dealing for personal, academic, research or non-commercial use, no part may be reproduced without written permission. The Department of Child Health Research is under no obligation to grant this permission. Please acknowledge the CAHS Research Education Program, Department of Child Health Research, Child and Adolescent Health Service when reproducing or quoting material from this source. Statistical Tips for Interpreting Scientific Claims CONTENTS: 1 PRESENTATION ............................................................................................................................... 1 2 ARTICLE: TWENTY TIPS FOR INTERPRETING SCIENTIFIC CLAIMS, SUTHERLAND, SPIEGELHALTER & BURGMAN, 2013 .................................................................................................................................. 15 3 -

Data Analysis Considerations in Producing 'Comparable' Information
Data Analysis Considerations in Producing ‘Comparable’ Information for Water Quality Management Purposes Lindsay Martin Griffith, Assistant Engineer, Brown and Caldwell Robert C. Ward, Professor, Colorado State University Graham B. McBride, Principal Scientist, NIWA (National Institute of Water and Atmospheric Research), Hamilton, New Zealand Jim C. Loftis, Professor, Colorado State University A report based on thesis material prepared by the lead author as part of the requirement for the degree of Master of Science from Colorado State University February 2001 ABSTRACT Water quality monitoring is being used in local, regional, and national scales to measure how water quality variables behave in the natural environment. A common problem, which arises from monitoring, is how to relate information contained in data to the information needed by water resource management for decision-making. This is generally attempted through statistical analysis of the monitoring data. However, how the selection of methods with which to routinely analyze the data affects the quality and comparability of information produced is not as well understood as may first appear. To help understand the connectivity between the selection of methods for routine data analysis and the information produced to support management, the following three tasks were performed. S An examination of the methods that are currently being used to analyze water quality monitoring data, including published criticisms of them. S An exploration of how the selection of methods to analyze water quality data can impact the comparability of information used for water quality management purposes. S Development of options by which data analysis methods employed in water quality management can be made more transparent and auditable. -

Who Uses Base Rates and <Emphasis Type="Italic">P </Emphasis>(D
Memory & Cognition 1998,26 (1), 161-179 Who uses base rates and P(D/,..,H)? An analysis ofindividual differences KEITHE. STANOVICH University ofToronto, Toronto, Ontario, Canada and RICHARD F. WEST James Madison University, Harrisonburg, Virginia In two experiments, involving over 900 subjects, we examined the cognitive correlates of the ten dency to view P(D/- H) and base rate information as relevant to probability assessment. Wefound that individuals who viewed P(D/- H) as relevant in a selection task and who used it to make the proper Bayesian adjustment in a probability assessment task scored higher on tests of cognitive ability and were better deductive and inductive reasoners. They were less biased by prior beliefs and more data driven on a covariation assessment task. In contrast, individuals who thought that base rates were rel evant did not display better reasoning skill or higher cognitive ability. Our results parallel disputes about the normative status of various components of the Bayesian formula in interesting ways. Itis ar gued that patterns of covariance among reasoning tasks may have implications for inferences about what individuals are trying to optimize in a rational analysis (J. R. Anderson, 1990, 1991). Twodeviations from normatively correct Bayesian rea and were asked to choose which pieces of information soning have been the focus ofmuch research. The two de they would need in order to determine whether the patient viations are most easily characterized ifBayes' rule is ex had the disease "Digirosa," The four pieces of informa pressed in the ratio form, where the odds favoring the focal tion were the percentage ofpeople with Digirosa, the per hypothesis (H) are derived by multiplying the likelihood centage of people without Digirosa, the percentage of ratio ofthe observed datum (D) by the prior odds favor people with Digirosa who have a red rash, and the per ing the focal hypothesis: centage ofpeople without Digirosa who have a red rash. -

Is Racial Profiling a Legitimate Strategy in the Fight Against Violent Crime?
Philosophia https://doi.org/10.1007/s11406-018-9945-1 Is Racial Profiling a Legitimate Strategy in the Fight against Violent Crime? Neven Sesardić1 Received: 21 August 2017 /Revised: 15 December 2017 /Accepted: 2 January 2018 # Springer Science+Business Media B.V., part of Springer Nature 2018 Abstract Racial profiling has come under intense public scrutiny especially since the rise of the Black Lives Matter movement. This article discusses two questions: (1) whether racial profiling is sometimes rational, and (2) whether it can be morally permissible. It is argued that under certain circumstances the affirmative answer to both questions is justified. Keywords Racial profiling . Discrimination . Police racism . Black lives matter. Bayes’s theorem . Base rate fallacy. Group differences 1 Introduction The Black Lives Matter (BLM) movement is driven by the belief that the police systematically discriminate against blacks. If such discrimination really occurs, is it necessarily morally unjustified? The question sounds like a provocation. For isn’t it obviously wrong to treat people differently just because they differ with respect to an inconsequential attribute like race or skin color? Indeed, racial profiling does go against Martin Luther King’s dream of a color-blind society where people Bwill not be judged by the color of their skin, but by the content of their character.^ The key question, however, is whether this ideal is achievable in the real world, as it is today, with some persistent statistical differences between the groups. Figure 1 shows group differences in homicide rates over a 29-year period, according to the Department of Justice (DOJ 2011:3): As we see (the red rectangle), the black/white ratio of the frequency of homicide offenders in these two groups is 7.6 (i.e., 34.4/4.5). -

Drøfting Og Argumentasjon
Bibliotekarstudentens nettleksikon om litteratur og medier Av Helge Ridderstrøm (førsteamanuensis ved OsloMet – storbyuniversitetet) Sist oppdatert 04.12.20 Drøfting og argumentasjon Ordet drøfting er norsk, og innebærer en diskuterende og problematiserende saksframstilling, med argumentasjon. Det er en systematisk diskusjon (ofte med seg selv). Å drøfte betyr å finne argumenter for og imot – som kan støtte eller svekke en påstand. Drøfting er en type kritisk tenking og refleksjon. Det kan beskrives som “systematisk og kritisk refleksjon” (Stene 2003 s. 106). Ordet brukes også som sjangerbetegnelse. Drøfting krever selvstendig tenkning der noe vurderes fra ulike ståsteder/ perspektiver. Den som drøfter, må vise evne til flersidighet. Et emne eller en sak ses fra flere sider, det veies for og imot noe, med styrker og svakheter, fordeler og ulemper. Den personen som drøfter, er på en måte mange personer, perspektiver og innfallsvinkler i én og samme person – først i sitt eget hode, og deretter i sin tekst. Idealet har blitt kalt “multiperspektivering”, dvs. å se noe fra mange sider (Nielsen 2010 s. 108). “Å drøfte er å diskutere med deg selv. En drøfting består av argumentasjon hvor du undersøker og diskuterer et fenomen fra flere sider. Drøfting er å kommentere og stille spørsmål til det du har redegjort for. Å drøfte er ikke bare å liste opp hva ulike forfattere sier, men å vise at det finnes ulike tolkninger og forståelser av hva de skriver om. Gjennom å vurdere de ulike tolkningene opp mot problemstillingen, foretar du en drøfting.” (https://student.hioa.no/argumentasjon-drofting-refleksjon; lesedato 19.10.18) I en drøfting inngår det å “vurdere fagkunnskap fra ulike perspektiver og ulike sider. -
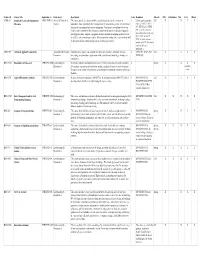
The Complete List of Courses, Including Course Descriptions, Prerequisites
Course ID Course Title Equivalent to Home Dept. Description Units Requisites Offered PhD Informatics MS Cert. Minor ACBS 513 Statistical Genetics for Quantitative ANS/GENE 513 Animal & Biomedical This course provide the student with the statistical tools to describe variation in 3 A basic genetic principles Fall X X X X Measures Sciences quantitative traits, particularly the decomposition of variation into genetic, environmental, course as ANS 213, GENE and gene by environment interaction components. Convariance (resemblance) between 433, GENE 533, or GENE relatives and heritability will be discussed, along with the topics of epistasis, oligogenic 545. A current course on and polygenic traits, complex segregation analysis, methods of mapping quantitative trait basic statistical principles as GENE 509C or MATH loci (QTL), and estimation procedures. Microarrays have multiple uses, each of which will 509C. A course in linear be discussed and the corresponding statistical analyses described. models as MATH 561 and in statistical inference mathematics. AREC 559 Advanced Applied Econometrics Agricultural & Resource Emphasis in the course is on econometric model specification, estimation, inference, 4 AREC 517, ECON 518, Fall X X X X Economics forecasting, and simulation. Applications with actual data and modeling techniques are ECON 549 emphasized. BIOS 576B Biostatistics for Research CPH/EPID 576B Epidemiology & Descriptive statistics and statistical inference relevant to biomedical research, including 3SpringXXX X Biostatistics data analysis, regression and correlation analysis, analysis of variance, survival analysis, available biological assay, statistical methods for epidemiology and statistical evaluation of clinical online literature. BIOS 576C Applied Biostatistics Analysis CPH/EPID 576C Epidemiology & Integrate methods in biostatistics (EPID 576A, B) and Epidemiology (EPID 573A, B) to 3 BIOS/EPID 576A, Fall X X X X Biostatistics develop analytical skills in an epidemiological project setting. -

Advanced Statistics for Environmental Professionals
Advanced Statistics for Environmental Professionals Bernard J. Morzuch Department of Resource Economics University of Massachusetts Amherst, Massachusetts [email protected] Table of Contents TOPIC PAGE How Does A Statistic Like A Sample Mean Behave? ................................................................................ 1 The Central Limit Theorem ........................................................................................................................ 3 The Standard Nonnal Distribution .............................................................................................................. 5 Statistical Estimation ................................................................................................................................... 5 The t-distribution ....................................................................................................................................... 13 Appearance Of The t-distribution ............................................................................................................. 14 Situation Where We Use t In Place Of z: Confidence Intervals ............................................................... 16 t-table ....................................................................................................................................................... 17 An Upper One-Sided (1-a) Confidence Interval For µ .......................................................................... 18 Another Confidence Interval Example................................................................