An Overview of Environmental Statistics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Data Analysis Considerations in Producing 'Comparable' Information
Data Analysis Considerations in Producing ‘Comparable’ Information for Water Quality Management Purposes Lindsay Martin Griffith, Assistant Engineer, Brown and Caldwell Robert C. Ward, Professor, Colorado State University Graham B. McBride, Principal Scientist, NIWA (National Institute of Water and Atmospheric Research), Hamilton, New Zealand Jim C. Loftis, Professor, Colorado State University A report based on thesis material prepared by the lead author as part of the requirement for the degree of Master of Science from Colorado State University February 2001 ABSTRACT Water quality monitoring is being used in local, regional, and national scales to measure how water quality variables behave in the natural environment. A common problem, which arises from monitoring, is how to relate information contained in data to the information needed by water resource management for decision-making. This is generally attempted through statistical analysis of the monitoring data. However, how the selection of methods with which to routinely analyze the data affects the quality and comparability of information produced is not as well understood as may first appear. To help understand the connectivity between the selection of methods for routine data analysis and the information produced to support management, the following three tasks were performed. S An examination of the methods that are currently being used to analyze water quality monitoring data, including published criticisms of them. S An exploration of how the selection of methods to analyze water quality data can impact the comparability of information used for water quality management purposes. S Development of options by which data analysis methods employed in water quality management can be made more transparent and auditable. -
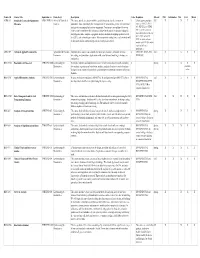
The Complete List of Courses, Including Course Descriptions, Prerequisites
Course ID Course Title Equivalent to Home Dept. Description Units Requisites Offered PhD Informatics MS Cert. Minor ACBS 513 Statistical Genetics for Quantitative ANS/GENE 513 Animal & Biomedical This course provide the student with the statistical tools to describe variation in 3 A basic genetic principles Fall X X X X Measures Sciences quantitative traits, particularly the decomposition of variation into genetic, environmental, course as ANS 213, GENE and gene by environment interaction components. Convariance (resemblance) between 433, GENE 533, or GENE relatives and heritability will be discussed, along with the topics of epistasis, oligogenic 545. A current course on and polygenic traits, complex segregation analysis, methods of mapping quantitative trait basic statistical principles as GENE 509C or MATH loci (QTL), and estimation procedures. Microarrays have multiple uses, each of which will 509C. A course in linear be discussed and the corresponding statistical analyses described. models as MATH 561 and in statistical inference mathematics. AREC 559 Advanced Applied Econometrics Agricultural & Resource Emphasis in the course is on econometric model specification, estimation, inference, 4 AREC 517, ECON 518, Fall X X X X Economics forecasting, and simulation. Applications with actual data and modeling techniques are ECON 549 emphasized. BIOS 576B Biostatistics for Research CPH/EPID 576B Epidemiology & Descriptive statistics and statistical inference relevant to biomedical research, including 3SpringXXX X Biostatistics data analysis, regression and correlation analysis, analysis of variance, survival analysis, available biological assay, statistical methods for epidemiology and statistical evaluation of clinical online literature. BIOS 576C Applied Biostatistics Analysis CPH/EPID 576C Epidemiology & Integrate methods in biostatistics (EPID 576A, B) and Epidemiology (EPID 573A, B) to 3 BIOS/EPID 576A, Fall X X X X Biostatistics develop analytical skills in an epidemiological project setting. -

Advanced Statistics for Environmental Professionals
Advanced Statistics for Environmental Professionals Bernard J. Morzuch Department of Resource Economics University of Massachusetts Amherst, Massachusetts [email protected] Table of Contents TOPIC PAGE How Does A Statistic Like A Sample Mean Behave? ................................................................................ 1 The Central Limit Theorem ........................................................................................................................ 3 The Standard Nonnal Distribution .............................................................................................................. 5 Statistical Estimation ................................................................................................................................... 5 The t-distribution ....................................................................................................................................... 13 Appearance Of The t-distribution ............................................................................................................. 14 Situation Where We Use t In Place Of z: Confidence Intervals ............................................................... 16 t-table ....................................................................................................................................................... 17 An Upper One-Sided (1-a) Confidence Interval For µ .......................................................................... 18 Another Confidence Interval Example................................................................ -

Environmental Statistics
Environmental statistics Вонр . проф . д-р Александар Маркоски Технички факултет – Битола 2008 год . Enviromatics 2008 - Environmental statistics 1 Introduction • Statistical analysis of environmental data is an important task to extract information on former and actual states of ecosystems. The estimates are known as sample statistics and form a base for prognoses on environmental system developments. • Topics of statistical analysis of environmental data are 1. Data analysis for the requirements of environmental administrations and associations (descriptive statistics, frequency distributions, averages, variances, error corrections, significance tests), 2. Data analysis for the requirements of different users as companies, farmers, tourists (explanatory statistics, multivariate statistics, time series analysis), 3. Basic research (regression and correlation analysis, multivariate statistics, advanced statistical techniques). Enviromatics 2008 - Environmental statistics 2 Environmental data • Environmental data are obtained by field samples and/or laboratory analysis . • They are directly observed (direct observations) or indirectly observed (due to calibration of analytical instruments and sensors). • Summary data are derived from statistics or by restricted observable indicators. • Simulated data are obtained by simulation models. • Measurement errors and outliers have to be removed from data sets. They will not take into account by data processing features. Enviromatics 2008 - Environmental statistics 3 Probability distributions of environmental data • Environmental data series represent the time and space varying behaviour of environmental processes. Some indicators show a long- wave cycling overlaid by short variations. Other indicators lay out stochastic fluctuations. Some indicators represent an unique behaviour with some peak events. Enviromatics 2008 - Environmental statistics 4 Statistical measures • Statistical measures of environmental data are represented by – averages , – variances and – measures of correlation . -

Douglas William Nychka
Douglas William Nychka Education 1978 B.A. Mathematics and Physics, Duke University 1983 Ph.D. Statistics, University of Wisconsin - Madison Honors and Awards 1978 Summa cum laude, Duke University 1978 Julia Dale Mathematics Award Duke University 2003 Fellow, American Statistical Association 2004 Jerry Sacks Award for Multidisciplinary Research 2013 Distinguished Achievement Award ENVR Section American Statistical Association 2013 Achievement Award, International Statistics and Climatology Meeting 2015 Fellow, Institute of Mathematical Statistics Professional Appointments 8/18 - present Professor, Department of Applied Mathematics and Statistics, Col- orado School of Mines, Golden, CO 8/97 - 8/18 National Center for Atmospheric Research, Boulder, CO. Visiting Scientist (8/97-7/99), Senior Scientist (8/99 - present), Project leader (8/99 - 9/04) Geophysical Statistics Project, Director (10/04 - 2017), Institute for Mathematics Applied to Geo- sciences (IMAGe) Senior Scientist Emeritus (8/18 - present) 7/83 - 6/99 Department of Statistics, North Carolina State University, Raleigh, NC Assistant (7/83 - 6/89), Associate (7/89 - 6/94) and Full Profes- sor (7/94 - 7/99), 1/94 - 7/03 National Institute of Statistical Sciences, Research Triangle Park, NC, Senior Fellow (1/94 -7/99) and Trustee (2000 - 2003) 6/93 and 6/08 Isaac Newton Institute for the Mathematical Sciences, Cambridge, England, Visiting Scholar 5/88 - 6/88, 6/92 Statistics Group, University of Bath, Bath, England, Visiting Faculty 7/89, 8/90 - 12/90 Operations Research and Industrial -

Statistical Concepts in Environmental Science
2 http://www.met.rdg.ac.uk/cag/courses/Stats/ Course Aim: To introduce the basic statistical concepts rel- evant to environmental science and to provide experience in the Statistical concepts correct use and interpretation of the various statistical methods currently used in the analysis of weather/climate observed and in environmental science model simulated data. Practical Exercises Each topic covered in the lectures will be Dr. David B. Stephenson followed by exercises analyzing real data in practical computing [email protected] classes using MINITAB statistical software. Department of Meteorology University of Reading Prerequisites Minimal statistical knowledge but some basic math- ematics and computer skills will be assumed. 10th January 2003 Course outline 1. Introduction \Some people hate the very name of stat- 2. Descriptive statistics istics but I ¯nd them full of beauty and in- 3. Basic probability concepts terest. Whenever they are not brutalized, 4. Probability distributions but delicately handled by the higher meth- 5. Parameter estimation ods, and are warily interpreted, their power 6. Statistical hypothesis testing of dealing with complicated phenomena is 7. Basic linear regression extraordinary." 8. Multiple and nonlinear regression - Sir Francis Galton 1 9. Introduction to time series 1 the person who invented the concept of correlation and the word anticyclone! 3 4 Acknowledgements The development of this course has bene¯ted from many stimulating dis- cussions with colleagues and students over the past few years. In particular, I wish to thank Nils Gunnar Kvamsto, Rasmus Benestad, and students at the University of Bergen for their helpful comments on the ¯rst version of this course. -

Environmental Data and Statistics - S
ENVIRONMENTAL SYSTEMS – Vol. II - Environmental Data and Statistics - S. Heiler ENVIRONMENTAL DATA AND STATISTICS S. Heiler Department of Mathematics and Statistics, University of Konstanz, Germany Keywords: environmental data, multivariate data, time series analysis, geostatistics, Space-time models. Contents 1. Introduction 2. Environmental Data 2.1 Data structures 2.1 Statistical graphics 3. Multivariate Data 3.1. Correlation analysis 3.1.1. The Bravais-Pearson correlation coefficient 3.1.2. Rank correlation 3.1.3. Correlation matrix 3.1.4. Multiple and partial correlation coefficient 3.1.5. Application to heavy metals in water 3.2. Regression 3.2.1. Simple Linear Regression 3.2.2. Non-parametric Regression 3.2.3. Multiple Linear Regression 3.2.4. Non-parametric Multiple Regression 3.3 Principal Components and Factor Analysis 3.3.1. Principal components analysis 3.3.2. Factor Analysis 3.4. Cluster analysis 3.5. Analysis of variance 4. Time Series Analysis 4.1. Introduction 4.2. Trend Estimation 4.3. Smoothing and Seasonal Estimation 4.4 Exponential smoothing 4.5. StationaryUNESCO Stochastic Processes – EOLSS 4.6. Univariate Linear Time Series Models 4.7. MultivariateSAMPLE Linear Time Series Models CHAPTERS 5. Geostatistics 5.1. Introduction 5.2. Homogeneous and Isotropic Random Fields 5.3. Inhomogeneities and Anisotopes 5.4. Space-time Models Acknowledgement Glossary Bibliography Biographical Sketch ©Encyclopedia of Life Support Systems (EOLSS) ENVIRONMENTAL SYSTEMS – Vol. II - Environmental Data and Statistics - S. Heiler Summary This review is a contribution on applications of statistical procedures to environmental data. Since this has become a very vast field, a comprehensive presentation seems to be impossible. -

Leveraging Probability Concepts for Genotype by Environment Recommendation
bioRxiv preprint doi: https://doi.org/10.1101/2021.04.21.440774; this version posted April 26, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-ND 4.0 International license. Leveraging probability concepts for genotype by environment recommendation Kaio O.G. Dias†1; Jhonathan P.R. dos Santos†1; Matheus D. Krause2; Hans-Peter Piepho3; Lauro J.M. Guimarães4; Maria M. Pastina4; Antonio A.F. Garcia 1* 1 Department of Genetics, Luiz de Queiroz College of Agriculture, University of São Paulo, SP, Brazil 2 Department of Agronomy, Iowa State University, Ames, IA, USA 3 Biostatistics Unit, University of Hohenheim, Stuttgart, Germany 4 Embrapa Maize and Sorghum, Sete Lagoas, MG, Brazil †These authors contributed equally to this work: Kaio Dias and Jhonathan dos Santos *Corresponding author: Antonio Garcia - [email protected] We would like to dedicate this article to the memory of Dr. Márcio Balestre. He was a young and brilliant scientist who made an outstanding contribution to statistical genetics. Abstract Statistical models that capture the phenotypic plasticity of a genotype across environments are crucial in plant breeding programs to potentially identify parents, generate offspring, and obtain highly productive genotypes for distinct environments. In this study, our aim is to leverage concepts of Bayesian models and probability methods of stability analysis to untangle genotype-by-environment interaction (GEI). The proposed method employs the posterior distribution obtained with the No-U-Turn sampler algorithm to get Monte Carlo estimates of adaptation and stability probabilities. -

MATH2740: Environmental Statistics
MATH2740: Environmental Statistics Lecturer: Andrew J. Baczkowski – room 11-13 – email: [email protected] Regularly updated information about the module is available on the internet at: http://www.maths.leeds.ac.uk/∼sta6ajb/math2715/math2740.html Module objective: To introduce statistical concepts and models for analysing data of an envi- ronmental nature: (a) analyse data of a spatial nature, (b) analyse models when applied to the analysis of categorical data arising from observational studies. Provisional detailed syllabus: 1. Types of data. 2. Spatial point patterns: contagious distributions. 3. Quadrant analysis: testing for non-randomness. 4. Distance methods: nearest neighbour analysis. 5. Spatial autocorrelation: join count statistics; testing hypotheses of spatial correlation. 6. Categorical data analysis: log-linear models; goodness of fit; three-dimensional tables; model selection. Booklist: No one book will be useful. References will be given for each lecture. Some useful textbooks include: Cressie, N.A.C. (1993) Statistics for Spatial Data. New York: Wiley. Diggle, P.J. (1983) Statistical Analysis of Spatial Point Patterns. London: Academic Press. Ripley, B.D. (1981) Spatial Statistics. New York: Wiley. Upton, G.J.G. and Fingleton, B. (1985) Spatial Data Analysis by Example. Volume I: Point Pattern and Quantitative Data. Wiley, Chichester. Agresti, A. (2002) Categorical Data Analysis. New Jersey: Wiley. Attendance: Attendance sheets will be circulated in each lecture for you to sign. Assessment: 80% of marks for two hour examination at end of semester and 20% of marks for continuous assessment comprising the exercise sheets and practicals. Examination paper: The examination paper will be in two parts. Part A will consist of twenty questions. -

Addressing Challenges of Hierarchical Structural Equation Modeling in Animal Agriculture
Addressing Challenges of Hierarchical Structural Equation Modeling in Animal Agriculture by Kessinee Chitakasempornkul B.BA., Mahidol University International Colleges, 2008 M.S., California State University Long Beach, 2012 AN ABSTRACT OF A DISSERTATION submitted in partial fulfillment of the requirements for the degree DOCTOR OF PHILOSOPHY Department of Statistics College of Arts and Sciences KANSAS STATE UNIVERSITY Manhattan, Kansas 2019 Abstract Feeding a world population of 9 billion people by 2050 is a fundamental challenge of our generation. Animal agriculture is positioned to play a major role on this challenge by ensuring a safe and secure supply of animal protein for food. Thus motivated, an understanding of the mechanistic interconnections between multiple outcomes in agricultural production systems is critical. Structural equation models (SEM) are being increasingly used for investigating directionality in the associations between outcomes in the system. Agricultural data pose peculiar challenges to the implementation of SEM, among them its structured architecture and its multidimensional heterogeneity. For example, observations on a given outcome collected at the animal level are often not mutually independent but rather likely to have correlation patterns due to clustering within pens or cohorts, which in turn may be subjected to common management or business practices defined at the level of a commercial operation. Also, agricultural outcomes of interest are often correlated and at multiple levels. Furthermore, a key assumption underlying SEM is that of a causal homogeneity, whereby the structural coefficients defining functional links in a network are assumed homogeneous and impervious to environmental conditions or management factors. This assumption seems particularly questionable in the context of animal agriculture, where production systems are regularly subjected to explicit interventions intended to optimize the necessary trade-offs between efficacy and efficiency of production. -

Statistics.Pdf
Analysis of Environmental Data Conceptual Foundations: Th e Ro le o f Statistic s in Enviro nm e ntal Re se arc h 1. The real world context of environmental research. 2 2. The role of statistics. 9 2.1 Description . 9 2.2 Inference. 12 3. The modeling process.. 17 4. The role of statistics, revisited. 20 Role of Statistics 2 1. The real world context of environmental research As scientists or managers we are faced with the challenges of defending our decisions every day. This is because we live in a world where challenges to the status quo are given little credence without solid evidence for the alternative (analogy: innocent until proven guilty). In other words, if we want to suggest a change to the current way of thinking, the burden of proof is on us. This idea lies at the core of the western scientific method. The classical approach to statistical inference, for example, involves testing hypotheses in which the null hypothesis (i.e., the status quo) is accepted unless there is overwhelming evidence in support of the alternative hypothesis – the one you are proposing. Indeed, we take great measures to ensure that we don’t falsely reject the null hypothesis in favor of the alternative (i.e., a Type I error); this is why by conventional standard we set the p- value for rejecting the null hypothesis to be a very small number, usually 0.05, which means that we will continue to support the null hypothesis unless the data suggest that there is less than a 5% chance that we would have observed our data if in fact the null hypothesis were true. -

Testing for Spatial Group-Wise Heteroskedasticity. a Specification Scan Test Procedure
Testing for Spatial Group-Wise Heteroskedasticity. A specification Scan test procedure. Autores y e-mail de la persona de contacto: Coro Chasco (Universidad Autónoma de Madrid) Julie Le Gallo (Université de Franche-Comté) Fernando A. López (Universidad Politécnica de Cartagena) Departamento: Métodos Cuantitativos e Informáticos Universidad: Politécnica de Cartagena Área Temática: (indicar el área temática en la que se inscribe el contenido de la comunicación) Resumen: Spatial heterogeneity is an important topic in the modelling of regional economies. In regression models, spatial heterogeneity can be reflected by varying coefficients (structural instability) and/or by varying error variances across observations forming blocks, what is called Spatial Group-Wise Heteroskedasticity. Spatial autocorrelation implies local clustering in the values of the variable and has been extensively studied in the literature. Unfortunately, testing for Spatial Group-Wise Heteroskedasticity is a less developed field. In this paper we present a novel and powerful procedure for Spatial Group-Wise Heteroskedasticity detection based on the Scan methodology. Palabras Clave: Spatial Group-Wise Heterokedasticity; Scan tests; Permutational approach; Monte Carlo. Clasificación JEL: C21; C50; R15 1. Introduction Spatial heterogeneity means that the behaviour of a certain spatial process is not uniform over space. We can think in different causes of instability (i) in the mean, (ii) in the variance or (iii) in both moments. Mean instability implies local clustering in the values of the variable and this topic has been studied extensively in the literature (Lesage and Pace, 2009, for a recent overview). In other cases, the source of instability is the variance. We are interested in the case of Spatial Group-Wise Heteroskedasticity, which means that the variability of the spatial data is systematically higher in some areas than in others.