DOCSLIB.ORG

Quantitative Genetic Models for the Balance Between Migration and Stabilizing Selection

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Quantitative Genetic Models for the Balance Between Migration and Stabilizing Selection Genet. Res., Camb. (2000), 76, pp. 285–293. With 3 figures. Printed in the United Kingdom # 2000 Cambridge University Press 285 Quantitative genetic models for the balance between migration and stabilizing selection JARLE TUFTO* Department of Mathematical Sciences – Lade section, Norwegian Uniersity of Science and Technology, 7491 Trondheim, Norway (Receied 15 July 1999 and in reised form 10Noember 1999) Summary The evolution of a quantitative trait subject to stabilizing selection and immigration, with the immigrants deviating from the local optimum, is considered under a number of different models of the underlying genetic basis of the trait. By comparing exact predictions under the infinitesimal model obtained using numerical methods with predictions of a simplified approximate model based on ignoring linkage disequilibrium, the increase in the expressed genetic variance as a result of linkage disequilibrium generated by migration is shown to be relatively small and negligible, provided that the genetic variance relative to the squared deviation of immigrants from the local optimum is sufficiently large or selection and migration is sufficiently weak. Deviation from normality is shown to be less important by comparing predictions of the infinitesimal model with a model presupposing normality. For a more realistic symmetric model, involving a finite number of loci only, no linkage and equal effects and frequencies across loci, additional changes in the genetic variance arise as a result of changes in underlying allele frequencies. Again, provided that the genetic variance relative to the squared deviation of the immigrants from the local optimum is small, the difference between the predictions of infinitesimal and the symmetric model are small unless the number of loci is very small. However, if the genetic variance relative to the squared deviation of the immigrants from the local optimum is large, or if selection and migration are strong, both linkage disequilibrium and changes in the genetic variance as a result of changes in underlying allele frequencies become important. (e.g. Felsenstein, 1977; Slatkin, 1978; Barton, 1999) is 1. Introduction available. Most species are divided into a number of smaller In general, exact predictions about the evolution of subpopulations connected by migration. Migration, quantitative traits assuming Mendelian inheritance in general, tends to homogenize a population and can cannot be made unless a large amount of detailed prevent adaptation of subpopulations to local en- information about the genetic basis of the trait is vironmental conditions. This is a relatively well available (Barton & Turelli, 1989). For a trait understood phenomenon when differences in fitness determined by n diallelic loci, there are 2n different are caused by genes at a single locus only (e.g. haplotypes, which, assuming random mating, implies Haldane, 1930; Slatkin, 1973, 1985; Nagylaki & that general analytic treatment of the effect of Lucier, 1979). Most traits, however, are quantitative, evolutionary forces such as selection, migration and that is, influenced by genes at many loci (Lande, reproduction seldom is possible. For only about 10 1982).Quantitative genetic theory involving both loci, the number of haplotypes also becomes so large selection and migration, despite being an important that numerical analysis becomes infeasible. Similarly, problem, is more sparse, although some theory while not increasing exponentially if one assumes focusing on geographic variation in quantitative traits additivity, the number of parameters to be estimated between demes (Bulmer, 1980, p. 180) and in clines in order to make prediction based on explicit multilocus models would typically require very large * Tel: j47 73591888. Fax: j47 73591038. e-mail: jarlet! math.ntnu.no amounts of data. Downloaded from https://www.cambridge.org/core. IP address: 170.106.35.234, on 24 Sep 2021 at 15:40:31, subject to the Cambridge Core terms of use, available at https://www.cambridge.org/core/terms. https://doi.org/10.1017/S0016672300004742 J. Tufto 286 Quantitative genetic evolutionary theory therefore as follows. In each generation, a proportion m of the has to be based on models relying on different degrees population is replaced by immigrants with mean of simplifying assumptions. The infinitesimal model breeding value z" and variance V". For simplicity, it is (Fisher, 1918; Bulmer, 1980) can be seen as a way of assumed that there is no linkage disequilibrium within overcoming the difficulties of explicit multilocus the immigrants. This will be approximately true if the models by assuming that the number of loci effectively immigrants originate from a single panmictic popu- is infinite and the allelic effects at individual loci are lation, deviating from the optimum as a result of, for additive and small. This approach reduces all genetic example, artificial selection. Migration is followed details to one parameter: the genetic variance at by stabilizing selection with fitness of individuals linkage disequilibrium VLE. Further simplifications of with phenotype P l ZjE equal to W!(P) l exp # the infinitesimal model, based on assuming normality (ks!(Pkz!) \2) such that the mean fitness of indi- or by ignoring the dynamics of the genetic variance, viduals with breeding value Z is proportional to W(Z) # are sometimes made in order to enable analytic l exp (ks(Zkz!) \2) where 1\s l 1\s!jVE. Without treatment of models of more specific evolutionary any loss of generality, we can let z! l 0 and z" l 1, situations. This is done, for example, in theory for the which is essentially equivalent to rescaling the model evolution of plasticity (Via & Lande, 1985; van in terms of z- by the deviation of the immigrants from Tienderen, 1997), theory of source-sink dynamics the local optimum z"kz!, remembering the VLE and s (Kirkpatrick & Barton, 1997) and in some non-spatial are now measured on this new dimensionless scale. models (e.g. Lande et al., 1997). An important question is therefore how well these different approximations 2. The infinitesimal model predict the evolutionary dynamics relative to more realistic models assuming finite number of loci, The assumption of the infinitesimal model that the deviations from normality and linkage disequilibrium. trait is affected by genes at an infinite number of loci Here I consider different approaches to modelling with infinitesimal and additive effects implies that the evolution of a population subject to local allele frequency changes will be infinitesimally small stabilizing selection with one-way immigration of so that there will be no change in the genetic variance individuals deviating from the local phenotypic of the genotypic values at linkage disequilibrium, VLE. optimum. This situation arises, for example, in models In addition, except for some patterns of strong linkage of source-sink dynamics (Holt & Gomulkiewicz, disequilibrium (Dawson, 1997), the distribution of 1997a, b) and in conservation genetics in the context genotypic values among offspring, conditional on the of reintroduction and intentional or unintentional genotypic values X and Y of selected parents, will supplementation of a wild population with individuals always be normal with expectation equal to the mid- kept in captivity (Hindar et al., 1991). In general, both parental value (XjY)\2 and variance equal to one stabilizing selection and migration will generate half the genetic variance at linkage equilibrium VLE linkage disequilibrium and consequently changes in (Bulmer, 1980; Turelli & Barton, 1994). The full the genetic variance. Unlike stabilizing Gaussian unconditional offspring distribution after repro- selection, however, migration will make the distri- duction, however, will depend on the distribution of bution of genotypic values depart from normality (e.g. parental genotypic values in the previous generation, Grant & Grant, 1994). More importantly, migration and does not need to be normal. will also pull the genotypic mean away from the local optimum, and thereby change the underlying allele (i) Exact Fourier transform method frequencies. The complexities of this situation make it Based on these general results, the joint effects of a good test of the various approaches to modelling migration, stabilizing selection and recombination on quantitative traits that have been proposed in the the distribution genotypic values can be found literature. numerically using the method of Turelli & Barton In the first part of the paper, exact predictions for (1994). Let ψ(z) be the initial distribution of the trait. the infinitesimal model obtained using numerical Migration changes this distribution to methods are compared with less realistic and simpler approaches based on ignoring departures from nor- ψh(z) l (1km)ψ(z)jmψ"(z), (1) mality and ignoring linkage disequilibrium altogether. where ψ"(z) is the (normal) distribution of the trait In the latter case a simple analytic result is available. among the immigrants. After selection the distribution In the second part of the paper, exact results for the of z is infinitesimal model are compared with a more realistic W(z)ψh(z) model involving a finite number of loci only and more ψd(z) l . (2) !W(z)ψ (z) specific details about the underlying genetic basis of h the trait. The life cycle is completed by reproduction, which is The details of the general evolutionary situation are equivalent to taking the mean of two randomly Downloaded from https://www.cambridge.org/core. IP address: 170.106.35.234, on 24 Sep 2021 at 15:40:31, subject to the Cambridge Core terms of use, available at https://www.cambridge.org/core/terms. https://doi.org/10.1017/S0016672300004742 Quantitatie genetic models for migration and stabilizing selection 287 After migration After selection After reproduction 4 2 0 4 2 0 4 2 0 4 2 0 Generations 1–7 4 2 0 4 2 0 4 2 0 –0·4 0 0·4 0·8 1·2 –0·4 0 0·4 0·8 1·2 –0·4 0 0·4 0·8 1·2 Fig. 1. Iterations of the infinitesimal mode for 7 generations (rows 1–7) with z! l 0, z" l 1, s l 1, m l 0n2, and VLE l 0n005, that is, immigrants deviating 14 genetic standard deviations from the optimum.
Load more

Recommended publications
  • An Introgression Analysis of Quantitative Trait Loci That Contribute to a Morphological Difference Between Drosophila Simulans and D
    Copyight 0 1997 by the Genetics Societv of America An Introgression Analysis of Quantitative Trait Loci That Contribute to a Morphological Difference Between Drosophila simulans and D. mauritiana Cathy C. Laurie, John R. True, Jianjun Liu and John M. Mercer Department of Zoology, Duke University, Durham, North Carolina 27708 Manuscript received August 12, 1996 Accepted for publication October 29, 1996 ABSTRACT Drosophila simulans and D. maum'tiana differ markedly in morphology of the posterior lobe, a male- specific genitalic structure. Bothsize and shapeof the lobe can be quantifiedby a morphometric variable, PC1, derived from principal components and Fourier analyses. The genetic architectureof the species difference in PC1 was investigated previously by composite interval mapping, which revealed largely additive inheritance, with a minimum of eight quantitative trait loci (QTL) affecting the trait. This analysis was extended by introgression of marked segments of the maun'tiana third chromosome into a simulans background by repeated backcrossing. Thetwo types of experiment are consistentin suggesting that several QTL on the third chromosome may have effects in the range of 10-15% of the parental difference andthat all or nearly all QTL have effects in the same direction. Since the parental difference is large (30.4 environmental standard deviations), effects of this magnitude can produce alternative homozygotes with little overlap in phenotype. However, these estimates may not reflect the effects of individual loci, since each interval or introgressed segment may contain multiple QTL. The consistent direction of allelic effects suggests a history of directional selection on the posterior lobe. HE genetic analysis of a quantitative trait usually ual genes that affect continuously variable traits.
    [Show full text]
  • Microevolution and the Genetics of Populations ​ ​ Microevolution Refers to Varieties Within a Given Type
    Chapter 8: Evolution Lesson 8.3: Microevolution and the Genetics of Populations ​ ​ Microevolution refers to varieties within a given type. Change happens within a group, but the descendant is clearly of the same type as the ancestor. This might better be called variation, or adaptation, but the changes are "horizontal" in effect, not "vertical." Such changes might be accomplished by "natural selection," in which a trait ​ ​ ​ ​ within the present variety is selected as the best for a given set of conditions, or accomplished by "artificial selection," such as when dog breeders produce a new breed of dog. Lesson Objectives ● Distinguish what is microevolution and how it affects changes in populations. ● Define gene pool, and explain how to calculate allele frequencies. ● State the Hardy-Weinberg theorem ● Identify the five forces of evolution. Vocabulary ● adaptive radiation ● gene pool ● migration ● allele frequency ● genetic drift ● mutation ● artificial selection ● Hardy-Weinberg theorem ● natural selection ● directional selection ● macroevolution ● population genetics ● disruptive selection ● microevolution ● stabilizing selection ● gene flow Introduction Darwin knew that heritable variations are needed for evolution to occur. However, he knew nothing about Mendel’s laws of genetics. Mendel’s laws were rediscovered in the early 1900s. Only then could scientists fully understand the process of evolution. Microevolution is how individual traits within a population change over time. In order for a population to change, some things must be assumed to be true. In other words, there must be some sort of process happening that causes microevolution. The five ways alleles within a population change over time are natural selection, migration (gene flow), mating, mutations, or genetic drift.
    [Show full text]
  • Patterns and Power of Phenotypic Selection in Nature
    Articles Patterns and Power of Phenotypic Selection in Nature JOEL G. KINGSOLVER AND DAVID W. PFENNIG Phenotypic selection occurs when individuals with certain characteristics produce more surviving offspring than individuals with other characteristics. Although selection is regarded as the chief engine of evolutionary change, scientists have only recently begun to measure its action in the wild. These studies raise numerous questions: How strong is selection, and do different types of traits experience different patterns of selection? Is selection on traits that affect mating success as strong as selection on traits that affect survival? Does selection tend to favor larger body size, and, if so, what are its consequences? We explore these questions and discuss the pitfalls and future prospects of measuring selection in natural populations. Keywords: adaptive landscape, Cope’s rule, natural selection, rapid evolution, sexual selection henotypic selection occurs when individuals with selection on traits that affect survival stronger than on those Pdifferent characteristics (i.e., different phenotypes) that affect only mating success? In this article, we explore these differ in their survival, fecundity, or mating success. The idea and other questions about the patterns and power of phe- of phenotypic selection traces back to Darwin and Wallace notypic selection in nature. (1858), and selection is widely accepted as the primary cause of adaptive evolution within natural populations.Yet Darwin What is selection, and how does it work? never attempted to measure selection in nature, and in the Selection is the nonrandom differential survival or repro- century following the publication of On the Origin of Species duction of phenotypically different individuals.
    [Show full text]
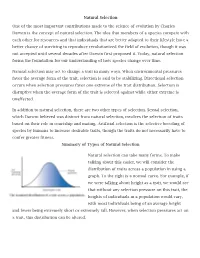
  • Natural Selection One of the Most Important Contributions Made to The
    Natural Selection One of the most important contributions made to the science of evolution by Charles Darwin is the concept of natural selection. The idea that members of a species compete with each other for resources and that individuals that are better adapted to their lifestyle have a better chance of surviving to reproduce revolutionized the field of evolution, though it was not accepted until several decades after Darwin first proposed it. Today, natural selection forms the foundation for our understanding of how species change over time. Natural selection may act to change a trait in many ways. When environmental pressures favor the average form of the trait, selection is said to be stabilizing. Directional selection occurs when selection pressures favor one extreme of the trait distribution. Selection is disruptive when the average form of the trait is selected against while either extreme is unaffected. In addition to natural selection, there are two other types of selection. Sexual selection, which Darwin believed was distinct from natural selection, involves the selection of traits based on their role in courtship and mating. Artificial selection is the selective breeding of species by humans to increase desirable traits, though the traits do not necessarily have to confer greater fitness. Summary of Types of Natural Selection Natural selection can take many forms. To make talking about this easier, we will consider the distribution of traits across a population in using a graph. To the right is a normal curve. For example, if we were talking about height as a trait, we would see that without any selection pressure on this trait, the heights of individuals in a population would vary, with most individuals being of an average height and fewer being extremely short or extremely tall.
    [Show full text]
  • Supplementary Information for Vyssotski, 2013
    Supplementary Information for Vyssotski, 2013 www.evolocus.com/evolocus/v1/evolocus-01-013-s.pdf Evolocus Supplementary Information for Transgenerational epigenetic compensation and sex u al d imorph ism 1,2,3 Dmitri L. Vyssotski Published 17 May 2013, Evolocus 1, 13-18 (2013): http://www.evolocus.com/evolocus/v1/evolocus-01-013.pdf In natu ral popu lation transgenerational epigenetic compensation is by unknown mechanisms, the mechanisms those were difficult to generated in h omoz y gou s mu tants, mainly in males. It d oes not imagine, and this possibility was abandoned for over 47 years. immed iately affect th e ph enoty pe of h omoz y gou s mu tants, w h ere The higher variability in males can be a result of a not so good it w as generated . Transgenerational epigenetic compensation is canalization of their ontogenesis, and the canalization of localiz ed not in th e same locu s as original mu tation and it is ontogenesis is modulated by sex hormones. Thus, we can d ominant, b ecau se it affects th e ph enoty pe ev en if it is receiv ed imagine that the canalization of ontogenesis in males is from one parent. In fu rth er generations, starting from F 2, it is more artificially decreased in comparison with females by means of ex pressed in females th an in males: it increases fitness of hormonal differences. h omozy gou s mu tant females, d ecreases fitness of w ild ty pe The shift of the female distribution to the right was not females and h as w eak effect on h eterozy gou s females.
    [Show full text]
  • Stabilizing Selection Shapes Variation in Phenotypic Plasticity
    bioRxiv preprint doi: https://doi.org/10.1101/2021.07.29.454146; this version posted July 29, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Stabilizing selection shapes variation in phenotypic plasticity 2 3 4 5 Dörthe Becker1,2,*, 6 Karen Barnard-Kubow1,3, 7 Robert Porter1, 8 Austin Edwards1,4, 9 Erin Voss1,5, 10 Andrew P. Beckerman2, 11 Alan O. Bergland1,* 12 13 14 1Department of Biology; University of Virginia, Charlottesville/VA, USA 15 2Department of Animal and Plant Sciences; University of Sheffield, Sheffield, UK 16 3Department of Biology, James Madison University, Harrisonburg/VA, USA 17 4Biological Imaging Development CoLab, University of California San Francisco, 18 San Francisco/CA, USA 19 5Department of Integrative Biology, University of California Berkeley, 20 Berkeley/CA 21 22 * to whom correspondence should be addressed: 23 DB ([email protected]), AOB ([email protected]) 24 25 26 27 Keywords: stabilizing selection; phenotypic plasticity; heritability; Daphnia; 28 defense morphologies 1 bioRxiv preprint doi: https://doi.org/10.1101/2021.07.29.454146; this version posted July 29, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 29 Abstract 30 The adaptive nature of phenotypic plasticity is widely documented in natural 31 populations. However, little is known about the evolutionary forces that shape 32 genetic variation in plasticity within populations. Here we empirically address this 33 issue by testing the hypothesis that stabilizing selection shapes genetic variation 34 in the anti-predator developmental plasticity of Daphnia pulex.
    [Show full text]
  • Selection on Breeding Date and Body Size in Colonizing Coho Salmon, Oncorhynchus Kisutch
    Molecular Ecology (2010) 19, 2562–2573 doi: 10.1111/j.1365-294X.2010.04652.x Selection on breeding date and body size in colonizing coho salmon, Oncorhynchus kisutch J. H. ANDERSON,* P. L. FAULDS,† W. I. ATLAS,‡ G. R. PESS§ and T. P. QUINN* *School of Aquatic and Fishery Sciences, University of Washington, Box 355020, Seattle, WA 98195, USA, †Seattle Public Utilities, 700 5th Avenue, Suite 4900, Seattle, WA, 98124, USA, ‡Department of Biological Sciences, Simon Fraser University, 8888 University Drive, Burnaby, BC, Canada V5A 1S6, §National Marine Fisheries Service, Northwest Fisheries Science Center, 2725 Montlake Boulevard East, Seattle, WA 98195, USA Abstract Selection during the colonization of new habitat is critical to the process of local adaptation, but has rarely been studied. We measured the form, direction, and strength of selection on body size and date of arrival to the breeding grounds over the first three cohorts (2003–2005) of a coho salmon (Oncorhynchus kisutch) population colonizing 33 km of habitat made accessible by modification of Landsburg Diversion Dam, on the Cedar River, Washington, USA. Salmon were sampled as they bypassed the dam, parentage was assigned based on genotypes from 10 microsatellite loci, and standardized selection gradients were calculated using the number of returning adult offspring as the fitness metric. Larger fish in both sexes produced more adult offspring, and the magnitude of the effect increased in subsequent years for males, suggesting that low densities attenuated traditional size-biased intrasexual competition. For both sexes, directional selection favoured early breeders in 2003, but stabilizing selection on breeding date was observed in 2004 and 2005.
    [Show full text]
  • An Evolutionary Perspective on Physical Attractiveness
    Evolutionary Anthropology 97 An Evolutionary Perspective on Physical Attractiveness DOUG JONES Everyday experience suggests that physical attractiveness is important in per- to others, and that mate choices based sonal-and especially sexual-relationships. This impression is confirmed by a on these preferences have evolution- large body of social psychological research.’ z2 Cross-cultural surveys and ethno- ary consequences. However, he did graphic accounts show that concern with the attractiveness of potential mates is not take up the question of where pref- also common in non-Westernsocietiesand in tribal and peasant cultures3 However, erences come from in the first place - social psychologists and anthropologists have often had a hard time explaining why e.g., why peahens prefer peacocks attractiveness should count for so much, or why some features rather than others with large and showy trains. In recent should seem particularly attractive. The theoretical difficulties in accounting for work on sexual selection and mate physical attraction are brought out in a Brazilian saying, “Beleza n2o p6e na mesa” choice,6,7 this question occupies a cen- (“Good looks don’t put anything on the table”), which points to the absence of any tral place. This work asks how natural evident practical advantage to choosing an attractive mate. Faced with these diffi- selection might affect mating prefer- culties, a growing number of researchers in biology, psychology, and anthropology ences and why one set of mating pref- have turned to the modern theory of sexual selection, which has been highly suc- erences might lead to greater cessful in explaining nonhuman animals’ attractions to traits of no direct ecological reproductive success than another.
    [Show full text]
  • Uncovering the Genetic Signature of Quantitative Trait Evolution with Replicated Time Series Data
    Heredity (2017) 118, 42–51 & 2017 Macmillan Publishers Limited, part of Springer Nature. All rights reserved 0018-067X/17 www.nature.com/hdy ORIGINAL ARTICLE Uncovering the genetic signature of quantitative trait evolution with replicated time series data SU Franssen, R Kofler and C Schlötterer The genetic architecture of adaptation in natural populations has not yet been resolved: it is not clear to what extent the spread of beneficial mutations (selective sweeps) or the response of many quantitative trait loci drive adaptation to environmental changes. Although much attention has been given to the genomic footprint of selective sweeps, the importance of selection on quantitative traits is still not well studied, as the associated genomic signature is extremely difficult to detect. We propose ‘Evolve and Resequence’ as a promising tool, to study polygenic adaptation of quantitative traits in evolving populations. Simulating replicated time series data we show that adaptation to a new intermediate trait optimum has three characteristic phases that are reflected on the genomic level: (1) directional frequency changes towards the new trait optimum, (2) plateauing of allele frequencies when the new trait optimum has been reached and (3) subsequent divergence between replicated trajectories ultimately leading to the loss or fixation of alleles while the trait value does not change. We explore these 3 phase characteristics for relevant population genetic parameters to provide expectations for various experimental evolution designs. Remarkably, over a broad range of parameters the trajectories of selected alleles display a pattern across replicates, which differs both from neutrality and directional selection. We conclude that replicated time series data from experimental evolution studies provide a promising framework to study polygenic adaptation from whole-genome population genetics data.
    [Show full text]
  • Biol2007 - Evolution of Quantitative Characters
    1 BIOL2007 - EVOLUTION OF QUANTITATIVE CHARACTERS How do evolutionary biologists measure variation in a typical quantitative character? Let’s use beak size in birds as a typical example. Phenotypic variation (Vp) in a quantitative character Some of the variation in beak size is caused by environmental factors (VE). Some of the variation is caused by genetic factors (VG). If there was no variation in genotype between birds then individuals would differ in beak size only because of different rearing environments. Quantitative geneticists think in terms of how the value of a character in an individual compares to the mean value of the character in the population. The population mean is taken to be a neutral measure and then particular phenotypes are increases or decreases from that value. AT LEVEL OF INDIVIDUAL Phenotype = genotype + environment P = G + E AT LEVEL OF POPULATION Phenotypic variance = genotypic variance + environmental variance VP = VG + VE Genotypic variance is divided into additive, dominance and interaction components VG = VA + VD + V I VA = Additive variance – due to the additive effects of individual alleles (inherited) VD = Dominance variance - reflect the combinations of alleles at each locus (homo- versus (homozygotes versus hetero-zygotes) in any given generation but are not inherited by offspring. An intra-locus effect. VI = Interaction/epistatic variance - reflect epistatic interactions between alleles at different loci. Again not passed onto offspring; they depend on particular combinations of genes in a given generation and are not inherited by offspring. An inter-locus effect. ___________________________________________________________ The following section (italicised) provides the alebgra to backup my assertion that VD and VI are not heritable.
    [Show full text]
  • Directional Selection Can Drive the Evolution of Modularity in Complex Traits
    Directional selection can drive the evolution of modularity in complex traits Diogo Melo1 and Gabriel Marroig Departamento de Genética e Biologia Evolutiva, Instituto de Biociências, Universidade de São Paulo, Sao Paulo, SP 05508-090, Brazil Edited by Stevan J. Arnold, Oregon State University, Corvallis, OR, and accepted by the Editorial Board December 2, 2014 (received for review December 9, 2013) Modularity is a central concept in modern biology, providing a promotes changes in only one trait of a module, the other traits powerful framework for the study of living organisms on many within this module will suffer an indirect selection pressure and organizational levels. Two central and related questions can be change as well, even if this response leads to lower fitness (8). This posed in regard to modularity: How does modularity appear in the indirect response in other traits is due to their genetic correlation first place, and what forces are responsible for keeping and/or with the selected trait. Understanding how traits become associated, changing modular patterns? We approached these questions using or correlated, is therefore a central question in evolutionary biology. a quantitative genetics simulation framework, building on pre- The question of how modular patterns evolve in each level of vious results obtained with bivariate systems and extending them complexity is still open to intense scrutiny (9–11). In morpho- to multivariate systems. We developed an individual-based model logical systems, one condition for the evolution of variational capable of simulating many traits controlled by many loci with pattern is the existence of genetic variation in the association variable pleiotropic relations between them, expressed in pop- between traits in a population.
    [Show full text]
  • Mutational Pleiotropy and the Strength of Stabilizing Selection Within and Between
    Genetics: Early Online, published on February 1, 2018 as 10.1534/genetics.118.300776 1 2 Mutational pleiotropy and the strength of stabilizing selection within and between 3 functional modules of gene expression 4 5 6 7 Julie M. Collet*1, Katrina McGuigan, Scott L. Allen, Stephen F. Chenoweth, Mark W. Blows 8 School of Biological Sciences, The University of Queensland, 4072, Australia 9 1current affiliation: CBGP, INRA, CIRAD, IRD, Montpellier SupAgro, Univ. Montpellier, 10 Montpellier, France 11 12 Data Archival Location: NCBI Gene Expression Omnibus (N lines: GSE49815; S lines: 13 GSE54777). 14 15 1 Copyright 2018. 16 Variational and functional modularity 17 Keywords: modularity, pleiotropy, genotype-phenotype map, Drosophila serrata, gene 18 expression 19 * corresponding author: [email protected] 20 ABSTRACT 21 Variational modules, sets of pleiotropically covarying traits, affect phenotypic evolution, and 22 therefore are predicted to reflect functional modules, such that traits within a variational 23 module also share a common function. Such an alignment of function and pleiotropy is 24 expected to facilitate adaptation by reducing the deleterious effects of mutations, and 25 allowing coordinated evolution of functionally related sets of traits. Here, we adopt a high- 26 dimensional quantitative genetic approach using a large number of gene expression traits in 27 Drosophila serrata to test whether functional grouping, defined by GO terms, predicts 28 variational modules. Mutational or standing genetic covariance was significantly greater 29 than among randomly grouped sets of genes for 38% of our functional groups, indicating 30 that GO terms can predict variational modularity to some extent. We estimated stabilizing 31 selection acting on mutational covariance to test the prediction that functional pleiotropy 32 would result in reduced deleterious effects of mutations within functional modules.
    [Show full text]