(NL-Bayes) Image Denoising Algorithm Marc Lebrun1, Antoni Buades2, Jean-Michel Morel3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Evaluating a BASIC Approach to Sensor Network Node Programming
Evaluating A BASIC Approach to Sensor Network Node Programming J. Scott Miller Peter A. Dinda Robert P. Dick [email protected] [email protected] [email protected] Northwestern University Northwestern University University of Michigan Abstract 1 Introduction Sensor networks have the potential to empower domain Wireless sensor networks (WSNs) can be viewed as experts from a wide range of fields. However, presently they general purpose distributed computing platforms defined by are notoriously difficult for these domain experts to program, their spatial presence and an emphasis on environment mon- even though their applications are often conceptually simple. itoring. The most prominent applications of sensor networks We address this problem by applying the BASIC program- have thus far included monitoring applications with a variety ming language to sensor networks and evaluating its effec- of requirements, although WSNs need not be limited to these tiveness. BASIC has proven highly successful in the past in tasks. While WSNs are currently of great research interest, it allowing novices to write useful programs on home comput- is ultimately communities and users outside of these areas— ers. Our contributions include a user study evaluating how application domain experts—that have the most to gain from well novice (no programming experience) and intermediate the functionality that WSNs can provide. We focus on ap- (some programming experience) users can accomplish sim- plication domain experts who are programming novices and ple sensor network tasks in BASIC and in TinyScript (a prin- not WSN experts. Our goal is to make the development of cipally event-driven high-level language for node-oriented WSN applications by such individuals and groups tractable programming) and an evaluation of power consumption is- and, ideally, straightforward. -

Computer Supplement #19 ***********************
THE CRYPTOGRAM Summer 1994 *********************** COMPUTER SUPPLEMENT #19 *********************** In this issue: PATTERN SEARCHING BY COMPUTER | D MELIORA describes a method and gives a Pascal program to perform pattern word searching. SWAGMAN | BOATTAIL has some help for solving basic transposition ciphers like SWAG- MAN, and includes his Cipher library. INTERNET MAILING LIST | Three of the Krewe have started an electronic mailing list to help in solving cryptograms. REVIEWS | DAEDALUS has recommendations for three books and a software package. GW-BASIC CRACKING | A program to decrypt protected GW-BASIC programs. HIGH PRECISION BASIC | Details about a dialect of BASIC that handles large numbers with ease. Plus: News and notes for computerists interested in cryptography, and cryptographers in- terested in computers. Published in association with the American Cryptogram Association INTRODUCTORY MATERIAL The ACA and Your Computer (1p). Background on the ACA for computerists. (As printed in ACA and You, 1988 edition; [Also on Issue Disk #11] Using Your Home Computer (1p). Ciphering at the ACA level with a computer. (As printed in ACA and You, 1988 edition). Frequently Asked Questions (approx. 20p) with answers, from the Usenet newsgroup sci.crypt. REFERENCE MATERIAL BASICBUGS - Bugs and errors in GW-BASIC (1p). [Also on Issue Disk #11]. BBSFILES - List of filenames and descriptions of cryptographic files available on the ACA BBS (files also available on disk via mail). BIBLIOG | A bibliography of computer magazine articles and books dealing with cryptography. (Updated August 89). [available on Issue Disk #11]. CRYPTOSUB - Complete listing of Cryptographic Substitution Program as published by PHOENIX in sections in The Cryptogram 1983{1985. -

Building Secure ASP.NET Applications: Authentication, Authorization, and Secure Communication
Building Secure ASP.NET Applications: Authentication, Authorization, and Secure Communication http://msdn.microsoft.com/library/default.asp?url=/library/en-us/dnnetsec/html/secnetlpMSDN.asp Roadmap J.D. Meier, Alex Mackman, Michael Dunner, and Srinath Vasireddy Microsoft Corporation November 2002 Applies to: Microsoft® .NET Framework version 1.0 ASP.NET Enterprise Services Web services .NET Remoting ADO.NET Visual Studio® .NET SQL™ Server Windows® 2000 Summary: This guide presents a practical, scenario driven approach to designing and building secure ASP.NET applications for Windows 2000 and version 1.0 of the .NET Framework. It focuses on the key elements of authentication, authorization, and secure communication within and across the tiers of distributed .NET Web applications. (This roadmap: 6 printed pages; the entire guide: 608 printed pages) Download Download Building Secure ASP.NET Applications in .pdf format. (1.67 MB, 608 printed pages) Contents What This Guide Is About Part I, Security Models Part II, Application Scenarios Part III, Securing the Tiers Part IV, Reference Who Should Read This Guide? What You Must Know Feedback and Support Collaborators Recommendations and sample code in the guide were built and tested using Visual Studio .NET Version 1.0 and validated on servers running Windows 2000 Advanced Server SP 3, .NET Framework SP 2, and SQL Server 2000 SP 2. What This Guide Is About This guide focuses on: • Authentication (to identify the clients of your application) • Authorization (to provide access controls for those clients) • Secure communication (to ensure that messages remain private and are not altered by unauthorized parties) Why authentication, authorization, and secure communication? Security is a broad topic. -

Mathematical Sciences Meetings and Conferences Section
page 1349 Calendar of AMS Meetings and Conferences Thla calandar lists all meetings which have been approved prior to Mathematical Society in the issue corresponding to that of the Notices the date this issue of Notices was sent to the press. The summer which contains the program of the meeting, insofar as is possible. and annual meetings are joint meetings of the Mathematical Associ Abstracts should be submitted on special forms which are available in ation of America and the American Mathematical Society. The meet many departments of mathematics and from the headquarters office ing dates which fall rather far in the future are subject to change; this of the Society. Abstracts of papers to be presented at the meeting is particularly true of meetings to which no numbers have been as must be received at the headquarters of the Society in Providence, signed. Programs of the meetings will appear in the issues indicated Rhode Island, on or before the deadline given below for the meet below. First and supplementary announcements of the meetings will ing. Note that the deadline for abstracts for consideration for pre have appeared in earlier issues. sentation at special sessions is usually three weeks earlier than that Abatracta of papara presented at a meeting of the Society are pub specified below. For additional information, consult the meeting an lished in the journal Abstracts of papers presented to the American nouncements and the list of organizers of special sessions. Meetings Abstract Program Meeting# Date Place Deadline Issue -
(Notes) Chapter: 1.1 Information Representation Topic
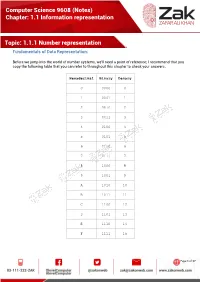
Computer Science 9608 (Notes) Chapter: 1.1 Information representation Topic: 1.1.1 Number representation Fundamentals of Data Representation: Before we jump into the world of number systems, we'll need a point of reference; I recommend that you copy the following table that you can refer to throughout this chapter to check your answers. Hexadecimal Binary Denary 0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 A 1010 10 B 1011 11 C 1100 12 D 1101 13 E 1110 14 F 1111 15 Page 1 of 17 Computer Science 9608 (Notes) Chapter: 1.1 Information representation Topic: 1.1.1 Number representation Denary/Decimal Denary is the number system that you have most probably grown up with. It is also another way of saying base 10. This means that there are 10 different numbers that you can use for each digit, namely: 0,1,2,3,4,5,6,7,8,9 Notice that if we wish to say 'ten', we use two of the numbers from the above digits, 1 and 0. Thousands Hundreds Tens Units 10^3 10^2 10^1 10^0 1000 100 10 1 5 9 7 3 Using the above table we can see that each column has a different value assigned to it. And if we know the column values we can know the number, this will be very useful when we start looking at other base systems. Obviously, the number above is: five-thousands, nine-hundreds, seven-tens and three-units. -

Palmtop 0)- Q) the New, Improved E :::::I Palmtop Paper Web Site •
o Editor's Message . ....•...... ..... .. o o u.s. $7.95 C\J Letters .•.. ..... .. ........ •..... : .... Q) ..c E New Products: What's New :::::I on the 2000 CD InfoBase? . .. 1 Z Palmtop 0)- Q) The New, Improved E :::::I Palmtop Paper Web Site •.... •........ 1( o > Ed gives a sneak preview of coming attractions on the ~per Palmtop Paper Web site. User to User: Uncovering Palmtop Possibilities at COMDEX ......... ... 1: Hal roams the halls of COMDEX with Mack Baggette tumin~ up Palmtop possibilities. The Next Three Years Should Be Exciting ..••...•• . .. ..... 11 A leading developer looks forward to several years of enhancements for the Palmtop. '}} j Through the Looking Glass: The Lotus Tapes ............ .. .. .. .. 7 If you've been looking for more and better information about Lotus1 ·2·3, the files on the 2000 CD InfoBase will end your search. It's all here! Palmtop Tips, Traps & Techniques The Psion Revo .... .. .............. 15 A reviewer for Byte.com puts this Palmtop contender through its paces. The HPLX-L Connection o U j ~ r 4J MORE Great Ideas from r 4J L.J the Online Palmtop Community! L.J World Wide Phone Guide ....•.. ... •. 1! What you need to hook up your modem just about anywhere in the world! Door to Door With the HP Palmtop . •.. .. •• •. ... 2: Idwide Phone Guide The Palmtop gets a new heft and feel and keeps a Malaysian sales force fully automated. \ CLJ'NNJ:CT up your MODEM anywhere on the PLANET! -.... ........--. The HPLX·L Connection ... .... .... 25 Palmtop Tips,Traps & Techniques •. •.. 28 02 COMDEX Files -

High-Level Structured Programming Platform for Wireless Sensor Networks
International Journal of Electronics and Electrical Engineering Vol. 2, No. 2, June, 2014 NTUPreter: High-Level Structured Programming Platform for Wireless Sensor Networks Yu-Cheng Norm Lien and Wen-Jong Wu Department of Engineering Science and Ocean Engineering, National Taiwan University, Taipei, Taiwan Email: [email protected], [email protected] Abstract—Wireless sensor networks have gained world-wide development environments currently requires users to attention in recent years, researches were proposed to code, compile and upload executable files by separate address challenges of sensor network programming. Making editors or command lines. These complicate procedures programming simple and flexible encourages users without confuse users. In most cases, learning the procedures is programming background to learn and adopt wireless often not their purpose. sensor network. We present the design of the NTUpreter, a remote programmable platform for wireless sensor network. The objective of this work is to decrease the This platform allows users to program senor nodes through programming effort by addressing the two mentioned a high-level structured programming language interpreter issues. Therefore, experts from different domains of and supports remote reprogramming therefore reduces the science and technology may benefit from this platform. In cost and effort of deployment. We also developed a language our work, we developed an interpreter that runs on sensor extension for the interpreter to access low-level hardware nodes to support high-level structured programming. and wireless functions. An integrated development Second, we provide users an integrated development environment (IDE) with steep learning curve is also environment with a clear and clean user interface. Last, introduced in this work. -
Ubasic User Guide
uBASIC User Guide (from ‘UBASIC/TutorialScratchpad’ @ CHDK Wiki) Draft 0.3, 17 July 2009, DanielF Contents Preface.................................................................................................................................... 4 Starting Out............................................................................................................................ 5 The Script Header .................................................................................................................. 6 The Basics of BASIC Programming...................................................................................... 7 Logic Commands ............................................................................................................... 7 The LET Command ................................................................................................... 7 The IF / THEN / ELSE Commands ........................................................................... 7 The FOR / TO / NEXT Commands ........................................................................... 7 Do / Until Loops ........................................................................................................ 8 While / Wend Loops .................................................................................................. 9 Subroutines using GOSUB (and related GOTO) Commands and Labels ................. 9 Sub-Routines.............................................................................................................. 9 GOSUB -
ENSIKLOPEDIA BASIS DATA Dan PROGRAM KOMPUTER
ENSIKLOPEDIA BASIS DATA dan PROGRAM KOMPUTER Dr. Janner Simarmata, M.Kom Haviluddin, M.Kom., Ph.D Ansari Saleh Ahmar, M.Sc Rahmat Hidayat, M.Sc.IT Daftar Isi Kata Pengantar Daftar Isi A……………………………………………………………….. B… ………………………………………………………………... C…………………………………………………………………... D…………………………………………………………………... E… ………………………………………………………………... F… ………………………………………………………………... G…………………………………………………………………... H..…..……………………………………………………………... I……..……………………………………………………………... J…..………………………………………………………………... K…………………………………………………………………... L….……………………………………………………………….. M…………………………………………………………………. N………………………………………………………………….. O………………………………………………………………….. P…………………………………………………………………... Q………………………………………………………………….. R…………………………………………………………………... S…………………………………………………………………... T…………………………………………………………………... 2 Kamus Istilah Basis Data dan Program Komputer U……..…………………………………………………………… V…………………………………………………………………. W………………………………………………………………… X………………………………………………………………….. Y………………………………………………………………….. Z………………………………………………………………….. Lampiran A Produk-Produk DBMS…………………………... Lampiran B Program-Program Sertifikasi…………………….. Lampiran C Diagram Bahasa Pemrograman………………… Lampiran D Bahasa Pemrograman dan Pembuatnya……….. Lampiran E Daftar-Daftar Singkatan…………………………. Daftar Isi………………………………………………………… A Abend Singkatan dari Absent By EnforcedNet Deprivation atau Ketidakhadiran disebabkan oleh paksaan ketaktersediaan jaringan. Istilah Abend untuk mendefinisikan proses penghentian sebuah program atau proses yang tidak normal diakibatkan oleh terjadinya kesalahan input data oleh user atau -

Ubasic User Guide
uBASIC User Guide (from ‘UBASIC/TutorialScratchpad’ @ CHDK Wiki) Draft 0.2, 20 June 2009, DanielF Contents Preface.................................................................................................................................... 4 Starting Out............................................................................................................................ 5 The Script Header .................................................................................................................. 5 The Basics of BASIC Programming...................................................................................... 7 Logic Commands ............................................................................................................... 7 The LET Command ................................................................................................... 7 The IF / THEN / ELSE Commands ........................................................................... 7 The FOR / TO / NEXT Commands ........................................................................... 7 Do / Until Loops ........................................................................................................ 8 While / Wend Loops .................................................................................................. 9 Subroutines using GOSUB (and related GOTO) Commands and Labels ................. 9 Sub-Routines.............................................................................................................. 9 GOSUB -

Appendix a Packages for Number Theory
Appendix A Packages for Number Theory There exist several computer packages which can profitably be used for number-theoretic computations. In this appendix, I will briefly describe the advantages and disadvantages of some of these systems. The oldest general-purpose symbolic algebra packages were written pri marily for physicists, and are not well suited for number theory. Furthermore (even for what they were designed for) they are very slow. On the other hand, they have been extensively tested, are have probably less bugs than more re cent systems. The two main systems in this category are Macsyma and Reduce. Reduce was extended by G. Collins to handle more efficiently computations linked to polynomials, and this gave rise to Sac-II, with a user interface called AIdes. These were the packages used in the 1970's. A second generation of packages was developed in the 1980's. They are much faster, better adapted to number theory, but having had less use, have more bugs. The two main commercial systems are Mathematica, by Wolfram Research, Inc., and Maple, by the University of Waterloo, Canada. Mathematica has a very nice user interface, and its plotting capabilities, for example on the Macintosh, are su perb. Maple is faster and often simpler to use, and has my preference. A third system is widely available, although not commercially released, the Scratch pad II system developed by IBM. This is a monster (in the same sense that ADA is a monster as a programming language). A subset of this system has recently been commercially released under the name Axiom. -

Linux and Open Source News
Newsletter of the Potomac Area Technology and Computer Society October 2013 www.patacs.org Page 1 Linux and Open Source News By Geof Goodrum, Potomac Area Technology and Computer Society linux(at)patacs.org Open Source for Canon Digital Cameras Override Camera parame- ters - Exposures from 2048s As owner of a Canon “Point and Shoot” (i.e., easy to to 1/60,000s with flash sync. use consumer model) digital camera, I was happy to Full manual or priority con- discover that camera enthusiasts have developed trol over exposure, aperture, Open Source software for a variety of Canon camera ISO and focus. models, including the Point and Shoot PowerShot Bracketing - Bracketing is supported for expo- Canon models and the high end Digital Single Lens sure, aperture, ISO, and even focus. Reflex (DSLR) cameras to give the cameras addi- tional features. Video Overrides - Control the quality or bitrate of video, or change it on the fly. Extended video The Canon Hack Development Kit (CHDK, clip length - 1 hour or 2GB. http://chdk.wikia.com/wiki/CHDK ) is a software pro- ject that supports a long list of Canon PowerShot Point Scripting - Control CHDK and camera features and Shoot models. The CHDK website provides a table using uBASIC and Lua scripts. Enables time of support camera models, links to stable and develop- lapse, motion detection, advanced bracketing, and ment versions of the software, and instructions on how much more. Many user-written scripts are availa- to install the software on SD cards. The CHDK soft- ble on the forum and wiki. ware does not replace the camera’s internal software Motion detection - Trigger exposure in response (firmware), but loads into the camera memory when to motion, fast enough to catch lightning.