Determining the Strength of Chess Players Based on Actual Play 3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Players Biel International Chess Festival
2009 Players Biel International Chess Festival Players Boris Gelfand Israel, 41 yo Elo: 2755 World ranking: 9 Date and place of birth: 24.6.1968, in Minsk (Belarus) Lives in: Rishon-le-Zion (Israel) Israel ranking: 1 Best world ranking: 3 (January 1991) In Biel GMT: winner in 1993 (Interzonal) and 2005. Other results: 3rd (1995, 1997, 2001), 4th (2000) Two Decades at the Top of Chess This is not a comeback, since Boris Gelfand never left the chess elite in the last twenty years. However, at the age of 41, the Israeli player has reached a new peak and is experiencing a a third wind. He is back in the world Top-10, officially as number 9 (in fact, a virtual number 5, if one takes into account his latest results that have not yet been recorded). He had not been ranked so high since 2006. Age does not seem to matter for this player who is unanimously appreciated in the field, both for his technical prowess and his personality. In Biel, he will not only be the senior player of the Grandmaster tournament, but also the top ranked and the Festival’s most loyal participant. Since his first appearance in 1993, he has come seven times to Biel; it is precisely at this Festival that he earned one of his greatest victories: in 1993, he finished first in the Interzonal Tournament (which, by then, was the only qualifying competition for the world championship), out of 73 participating grandmasters (including Anand and Kramnik). His victory in Biel against Anand is mentioned in his book, My Most Memorable Games. -

Videos Bearbeiten Im Überblick: Sieben Aktuelle VIDEOSCHNITT Werkzeuge Für Den Videoschnitt
Miller: Texttool-Allrounder Wego: Schicke Wetter-COMMUNITY-EDITIONManjaro i3: Arch-Derivat mit bereitet CSVs optimal auf S. 54 App für die Konsole S. 44 Tiling-Window-Manager S. 48 Frei kopieren und beliebig weiter verteilen ! 03.2016 03.2016 Guter Schnitt für Bild und Ton, eindrucksvolle Effekte, perfektes Mastering VIDEOSCHNITT Videos bearbeiten Im Überblick: Sieben aktuelle VIDEOSCHNITT Werkzeuge für den Videoschnitt unter Linux im Direktvergleich S. 10 • Veracrypt • Wego • Wego • Veracrypt • Pitivi & OpenShot: Einfach wie noch nie – die neue Generation der Videoschnitt-Werkzeuge S. 20 Lightworks: So kitzeln Sie optimale Ergebnisse aus der kostenlosen Free-Version heraus S. 26 Verschlüsselte Daten sicher verstecken S. 64 Glaubhafte Abstreitbarkeit: Wie Sie mit dem Truecrypt-Nachfolger • SQLiteStudio Stellarium Synology RT1900ac Veracrypt wichtige Daten unauffindbar in Hidden Volumes verbergen Stellarium erweitern S. 32 Workshop SQLiteStudio S. 78 Eigene Objekte und Landschaften Die komfortable Datenbankoberfläche ins virtuelle Planetarium einbinden für Alltagsprogramme auf dem Desktop Top-Distris • Anydesk • Miller PyChess • auf zwei Heft-DVDs ANYDESK • MILLER • PYCHESS • STELLARIUM • VERACRYPT • WEGO • • WEGO • VERACRYPT • STELLARIUM • PYCHESS • MILLER • ANYDESK EUR 8,50 EUR 9,35 sfr 17,00 EUR 10,85 EUR 11,05 EUR 11,05 2 DVD-10 03 www.linux-user.de Deutschland Österreich Schweiz Benelux Spanien Italien 4 196067 008502 03 Editorial Old and busted? Jörg Luther Chefredakteur Sehr geehrte Leserinnen und Leser, viele kleinere, innovative Distributionen seit einem Jahrzehnt kommen Desktop- Immer öfter stellen wir uns aber die haben damit erst gar nicht angefangen und Notebook-Systeme nur noch mit Frage, ob es wirklich noch Sinn ergibt, oder sparen es sich schon lange. Open- 64-Bit-CPUs, sodass sich die Zahl der moderne Distributionen überhaupt Suse verzichtet seit Leap 42.1 darauf; das 32-Bit-Systeme in freier Wildbahn lang- noch als 32-Bit-Images beizulegen. -

The 12Th Top Chess Engine Championship
TCEC12: the 12th Top Chess Engine Championship Article Accepted Version Haworth, G. and Hernandez, N. (2019) TCEC12: the 12th Top Chess Engine Championship. ICGA Journal, 41 (1). pp. 24-30. ISSN 1389-6911 doi: https://doi.org/10.3233/ICG-190090 Available at http://centaur.reading.ac.uk/76985/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . To link to this article DOI: http://dx.doi.org/10.3233/ICG-190090 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online TCEC12: the 12th Top Chess Engine Championship Guy Haworth and Nelson Hernandez1 Reading, UK and Maryland, USA After the successes of TCEC Season 11 (Haworth and Hernandez, 2018a; TCEC, 2018), the Top Chess Engine Championship moved straight on to Season 12, starting April 18th 2018 with the same divisional structure if somewhat evolved. Five divisions, each of eight engines, played two or more ‘DRR’ double round robin phases each, with promotions and relegations following. Classic tempi gradually lengthened and the Premier division’s top two engines played a 100-game match to determine the Grand Champion. The strategy for the selection of mandated openings was finessed from division to division. -

World Stars Sharjah Online International Chess Championship 2020
World Stars Sharjah Online International Chess Championship 2020 World Stars 2020 ● Tournament Book ® Efstratios Grivas 2020 1 Welcome Letter Sharjah Cultural & Chess Club President Sheikh Saud bin Abdulaziz Al Mualla Dear Participants of the World Stars Sharjah Online International Chess Championship 2020, On behalf of the Board of Directors of the Sharjah Cultural & Chess Club and the Organising Committee, I am delighted to welcome all our distinguished participants of the World Stars Sharjah Online International Chess Championship 2020! Unfortunately, due to the recent negative and unpleasant reality of the Corona-Virus, we had to cancel our annual live events in Sharjah, United Arab Emirates. But we still decided to organise some other events online, like the World Stars Sharjah Online International Chess Championship 2020, in cooperation with the prestigious chess platform Internet Chess Club. The Sharjah Cultural & Chess Club was founded on June 1981 with the object of spreading and development of chess as mental and cultural sport across the Sharjah Emirate and in the United Arab Emirates territory in general. As on 2020 we are celebrating the 39th anniversary of our Club I can promise some extra-ordinary events in close cooperation with FIDE, the Asian Chess Federation and the Arab Chess Federation for the coming year 2021, which will mark our 40th anniversary! For the time being we welcome you in our online event and promise that we will do our best to ensure that the World Stars Sharjah Online International Chess Championship -

CHESS TOURNAMENT MARKETING SUPPORT by Purple Tangerine COMMERCIAL SPONSORSHIP & PARTNERSHIP OPPORTUNITIES
COMMERCIAL SPONSORSHIP & PARTNERSHIP OPPORTUNITIES PRO-BIZ CHALLENGE 2016 Now in it’s 5th year, the Pro-Biz Challenge is the starter event for the London Chess Classic giving business people and their companies the SCHEDULE opportunity of a lifetime: to team up with one of their chess heroes! ACTIVITY VENUES TIMING Pro-Biz Challenge Press Launch Central London Host Partner tbc It brings the best business minds and the world’s leading Grand Masters PR Fund Raising Event Central London Host Partner September together in a fun knockout tournament to raise money for the UK charity, Chess in Schools and Communities (CSC). Businesses can bid to play with Pro-Biz Challenge Final Central London Host Partner December their favourite players and the ones who bid the highest get the chance to team up with a Grand Master. In 2014, the Pro-Biz Challenge included a team featuring rugby legend Sir Clive Woodward, who teamed up with leading British GM Gawain Jones. They fought hard, but after a three-round knockout, the top honours went to Anish Giri and Rajko Vujatovic of Bank of America. The current Champions are: Hikaru Nakamura (USA) and Josip Asik, CEO of Chess Informant. QUICK FACTS TEAMS 8 teams of two – one Company (Amateur Player) and one Grand Master from the London Chess Classic RAPID PLAY The Company Player (Amateur) and Grand Master in each team will take it in turns to make moves in Rapid Play games, FORMAT with each team allowed two one-minute time-outs per game to discuss strategy or perhaps just a killer move PRIZE Bragging Rights and -

Here Should That It Was Not a Cheap Check Or Spite Check Be Better Collaboration Amongst the Federations to Gain Seconds
Chess Contents Founding Editor: B.H. Wood, OBE. M.Sc † Executive Editor: Malcolm Pein Editorial....................................................................................................................4 Editors: Richard Palliser, Matt Read Malcolm Pein on the latest developments in the game Associate Editor: John Saunders Subscriptions Manager: Paul Harrington 60 Seconds with...Chris Ross.........................................................................7 Twitter: @CHESS_Magazine We catch up with Britain’s leading visually-impaired player Twitter: @TelegraphChess - Malcolm Pein The King of Wijk...................................................................................................8 Website: www.chess.co.uk Yochanan Afek watched Magnus Carlsen win Wijk for a sixth time Subscription Rates: United Kingdom A Good Start......................................................................................................18 1 year (12 issues) £49.95 Gawain Jones was pleased to begin well at Wijk aan Zee 2 year (24 issues) £89.95 3 year (36 issues) £125 How Good is Your Chess?..............................................................................20 Europe Daniel King pays tribute to the legendary Viswanathan Anand 1 year (12 issues) £60 All Tied Up on the Rock..................................................................................24 2 year (24 issues) £112.50 3 year (36 issues) £165 John Saunders had to work hard, but once again enjoyed Gibraltar USA & Canada Rocking the Rock ..............................................................................................26 -
Draft – Not for Circulation
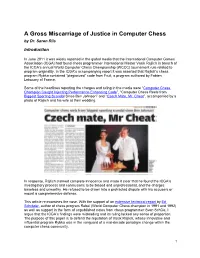
A Gross Miscarriage of Justice in Computer Chess by Dr. Søren Riis Introduction In June 2011 it was widely reported in the global media that the International Computer Games Association (ICGA) had found chess programmer International Master Vasik Rajlich in breach of the ICGA‟s annual World Computer Chess Championship (WCCC) tournament rule related to program originality. In the ICGA‟s accompanying report it was asserted that Rajlich‟s chess program Rybka contained “plagiarized” code from Fruit, a program authored by Fabien Letouzey of France. Some of the headlines reporting the charges and ruling in the media were “Computer Chess Champion Caught Injecting Performance-Enhancing Code”, “Computer Chess Reels from Biggest Sporting Scandal Since Ben Johnson” and “Czech Mate, Mr. Cheat”, accompanied by a photo of Rajlich and his wife at their wedding. In response, Rajlich claimed complete innocence and made it clear that he found the ICGA‟s investigatory process and conclusions to be biased and unprofessional, and the charges baseless and unworthy. He refused to be drawn into a protracted dispute with his accusers or mount a comprehensive defense. This article re-examines the case. With the support of an extensive technical report by Ed Schröder, author of chess program Rebel (World Computer Chess champion in 1991 and 1992) as well as support in the form of unpublished notes from chess programmer Sven Schüle, I argue that the ICGA‟s findings were misleading and its ruling lacked any sense of proportion. The purpose of this paper is to defend the reputation of Vasik Rajlich, whose innovative and influential program Rybka was in the vanguard of a mid-decade paradigm change within the computer chess community. -

London Chess Classic, Round 5
PRESS RELEASE London Chess Classic, Round 5 SUPER FABI GOES BALLISTIC , OTHERS LOSE THEIR FOCUS ... John Saunders reports: The fifth round of the 9th London Chess Classic, played on Wednesday 6 December 2017 at the Olympia Conference Centre, saw US number one Fabiano Caruana forge clear of the field by a point after winning his second game in a row, this time against ex-world champion Vishy Anand. Tournament leader Fabiano Caruana talks to Maurice Ashley in the studio (photo Lennart Ootes) It ’s starting to look like a one-man tournament. Caruana has won two games, the other nine competitors not one between them. We ’ve only just passed the mid-point of the tournament, of course, so it could all go wrong for him yet but it would require a sea change in the pacific nature of the tournament for this to happen. Minds are starting to go back to Fabi ’s wonder tournament, the Sinquefield Cup of 2014 when he scored an incredible 8 ½/10 to finish a Grand Canyon in points ahead of Carlsen, Topalov, Aronian, Vachier-Lagrave and Nakamura. That amounted to a tournament performance rating of 3103 which is so off the scale for these things that it doesn ’t even register on the brain as a feasible Elo number. Only super-computers usually scale those heights. For Fabi to replicate that achievement he would have to win all his remaining games in London. But he won ’t be worrying about the margin of victory so much as finishing first. He needs to keep his mind on his game and I won ’t jinx his tournament any further with more effusive comments. -

The USCF Elo Rating System by Steven Craig Miller
The USCF Elo Rating System By Steven Craig Miller The United States Chess Federation’s Elo rating system assigns to every tournament chess player a numerical rating based on his or her past performance in USCF rated tournaments. A rating is a number between 0 and 3000, which estimates the player’s chess ability. The Elo system took the number 2000 as the upper level for the strong amateur or club player and arranged the other categories above and below, as shown in the table below. Mr. Miller’s USCF rating is slightly World Championship Contenders 2600 above 2000. He will need to in- Most Grandmasters & International Masters crease his rating by 200 points (or 2400 so) if he is to ever reach the level Most National Masters of chess “master.” Nonetheless, 2200 his meager 2000 rating puts him in Candidate Masters / “Experts” the top 6% of adult USCF mem- 2000 bers. Amateurs Class A / Category 1 1800 In the year 2002, the average rating Amateurs Class B / Category 2 for adult USCF members was 1429 1600 (the average adult rating usually Amateurs Class C / Category 3 fluctuates somewhere around 1400 1500). The average rating for scho- Amateurs Class D / Category 4 lastic USCF members was 608. 1200 Novices Class E / Category 5 Most USCF scholastic chess play- 1000 ers will have a rating between 100 Novices Class F / Category 6 and 1200, although it is not un- 800 common for a few of the better Novices Class G / Category 7 players to have even higher ratings. 600 Novices Class H / Category 8 Ratings can be provisional or estab- 400 lished. -

Elo World, a Framework for Benchmarking Weak Chess Engines
Elo World, a framework for with a rating of 2000). If the true outcome (of e.g. a benchmarking weak chess tournament) doesn’t match the expected outcome, then both player’s scores are adjusted towards values engines that would have produced the expected result. Over time, scores thus become a more accurate reflection DR. TOM MURPHY VII PH.D. of players’ skill, while also allowing for players to change skill level. This system is carefully described CCS Concepts: • Evaluation methodologies → Tour- elsewhere, so we can just leave it at that. naments; • Chess → Being bad at it; The players need not be human, and in fact this can facilitate running many games and thereby getting Additional Key Words and Phrases: pawn, horse, bishop, arbitrarily accurate ratings. castle, queen, king The problem this paper addresses is that basically ACH Reference Format: all chess tournaments (whether with humans or com- Dr. Tom Murphy VII Ph.D.. 2019. Elo World, a framework puters or both) are between players who know how for benchmarking weak chess engines. 1, 1 (March 2019), to play chess, are interested in winning their games, 13 pages. https://doi.org/10.1145/nnnnnnn.nnnnnnn and have some reasonable level of skill. This makes 1 INTRODUCTION it hard to give a rating to weak players: They just lose every single game and so tend towards a rating Fiddly bits aside, it is a solved problem to maintain of −∞.1 Even if other comparatively weak players a numeric skill rating of players for some game (for existed to participate in the tournament and occasion- example chess, but also sports, e-sports, probably ally lose to the player under study, it may still be dif- also z-sports if that’s a thing). -

The SSDF Chess Engine Rating List, 2019-02
The SSDF Chess Engine Rating List, 2019-02 Article Accepted Version The SSDF report Sandin, L. and Haworth, G. (2019) The SSDF Chess Engine Rating List, 2019-02. ICGA Journal, 41 (2). 113. ISSN 1389- 6911 doi: https://doi.org/10.3233/ICG-190107 Available at http://centaur.reading.ac.uk/82675/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . Published version at: https://doi.org/10.3233/ICG-190085 To link to this article DOI: http://dx.doi.org/10.3233/ICG-190107 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online THE SSDF RATING LIST 2019-02-28 148673 games played by 377 computers Rating + - Games Won Oppo ------ --- --- ----- --- ---- 1 Stockfish 9 x64 1800X 3.6 GHz 3494 32 -30 642 74% 3308 2 Komodo 12.3 x64 1800X 3.6 GHz 3456 30 -28 640 68% 3321 3 Stockfish 9 x64 Q6600 2.4 GHz 3446 50 -48 200 57% 3396 4 Stockfish 8 x64 1800X 3.6 GHz 3432 26 -24 1059 77% 3217 5 Stockfish 8 x64 Q6600 2.4 GHz 3418 38 -35 440 72% 3251 6 Komodo 11.01 x64 1800X 3.6 GHz 3397 23 -22 1134 72% 3229 7 Deep Shredder 13 x64 1800X 3.6 GHz 3360 25 -24 830 66% 3246 8 Booot 6.3.1 x64 1800X 3.6 GHz 3352 29 -29 560 54% 3319 9 Komodo 9.1 -

Python-Chess Release 1.0.0 Unknown
python-chess Release 1.0.0 unknown Sep 24, 2020 CONTENTS 1 Introduction 3 2 Documentation 5 3 Features 7 4 Installing 11 5 Selected use cases 13 6 Acknowledgements 15 7 License 17 8 Contents 19 8.1 Core................................................... 19 8.2 PGN parsing and writing......................................... 35 8.3 Polyglot opening book reading...................................... 42 8.4 Gaviota endgame tablebase probing................................... 44 8.5 Syzygy endgame tablebase probing................................... 45 8.6 UCI/XBoard engine communication................................... 47 8.7 SVG rendering.............................................. 58 8.8 Variants.................................................. 59 8.9 Changelog for python-chess....................................... 61 9 Indices and tables 93 Index 95 i ii python-chess, Release 1.0.0 CONTENTS 1 python-chess, Release 1.0.0 2 CONTENTS CHAPTER ONE INTRODUCTION python-chess is a pure Python chess library with move generation, move validation and support for common formats. This is the Scholar’s mate in python-chess: >>> import chess >>> board= chess.Board() >>> board.legal_moves <LegalMoveGenerator at ... (Nh3, Nf3, Nc3, Na3, h3, g3, f3, e3, d3, c3, ...)> >>> chess.Move.from_uci("a8a1") in board.legal_moves False >>> board.push_san("e4") Move.from_uci('e2e4') >>> board.push_san("e5") Move.from_uci('e7e5') >>> board.push_san("Qh5") Move.from_uci('d1h5') >>> board.push_san("Nc6") Move.from_uci('b8c6') >>> board.push_san("Bc4") Move.from_uci('f1c4')