A Recursive Solution for Power-Transmission Loss in DC-Powered Networks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HKRI Taikoo Hui Shanghai
FACT SHEET HKRI Taikoo Hui Shanghai Located in the heart of West Nanjing Road CBD, Jing’an District, Shanghai, HKRI Taikoo Hui is a 50:50 joint venture between two Hong Kong listed companies, HKR International and Swire Properties. The development comprises a lifestyle shopping mall, two premium Grade A office towers, two boutique hotels and one serviced residence, an underground shopping corridor, providing a mixed-use space for working, shopping, dining, leisure and living enjoyment. Location :West Nanjing Road CBD,Shanghai Opening year :Opened in phases from the second half of 2016 Developer :HKR International Limited (50%) Swire Properties Limited (50%) Architect :Wong & Ouyang (HK) Limited – Architect Architect MAKE AECOM Environmental Planning and Design (Shanghai) Co.,td. –Structural engineer Parsons Brinckerhoff (Asia) Ltd. –Building services engineer Total site area :Approx. 63,000 sqm / approx. 676,000 sq ft Gross floor area :Total GFA approx. 322,000 sqm / over 3.46 million sq ft A lifestyle shopping mall – HKRI Taikoo Hui (Approx. 100,000 sqm / approx. 1.078 million sq ft) Two office towers – HKRI Centre one and HKRI Centre two (over 170,000 sqm/ approx. 1,85 million sq ft) Two boutique hotels and one serviced apartments – The Sukhothai Shanghai – The Middle House and The Middle House Residences (over 50,000 sqm/ approx. 538,195 sq ft, with more than 400 rooms in total) One commercial metro space – MetroLink (over 3,000 sqm/ approx. 3,600 sq ft) Parking space :Approx. 1,200 Accessibility :The Complex has a direct access to Metro Line 13, with Line 2 and Line 12 at West Nanjing Road station only waking distance away. -

OG D EN T UT
~fiz Form 990 Return of Organization Exempt From Income Tax Under section 501(c), 527, or 4947(a)(1) of the Internal Revenue Code (except black lung 2002 benefit trust or pmate foundation) Open to Pul The organization may have b use a copy of Nia realm to ss~sty state reporting requirements ~f19pBCt101 A For the 2002 calendar or tax ear be loom and ending B Check d applicable Plea! C Name of organization D Employer ID number use IF '2A _1ZQnQlQ Address change label Name charge print E Telephone number Instal return typo Number and street (or P O box d mail is not delivered to street address) RooMSUde 330-535-8116 Final return See F Accounting method N Cash Specil Amended velum City or town state or country and ZIP " 4 Puluai InsW 11 0 Other specify) Application pendin, thin fliSectlon 501(c)(3) orpanlraUOns and 4B47(a)(1) nonexempt charitable H and I are not applicable to section 527 organizations trusts muss attach a completed Schedule A (Form 990 or 990F2) H(a) Is this a group return for affilutesl O Yes ~ No G Wabsrte t orianahOU52 . CO[TI H(b) If 'Yes' enter no of affiliates J Organization type H(C) Are all affiliates inclwed? a Yes ~ No check on one 1 501 c 3 s insert no 4947 (,)( 1 ) or 527 (If'NO' an a list See msir ) K Check here 1 u if the organization's gross receipts are normally not more than H(d) Is this a separate return fled by an $25,000 The organization need not file a return with the IRS, but if the organization Yes I I No received a Form 990 Package in we mail, it should file a return without financial dale I 41 dGEN -

Download Brochure
ABOUT THE HOUSE Welcome to The Middle House An elegant and calm oasis amidst the dynamic backdrop of one of Residences, you’ll relish every moment of your stay. Take in the Asia’s most urban cities, The Middle House is nestled in the heart of elegant interiors by Milan-based architect and designer Piero Lissoni, Shanghai – its name a nod to its location in the historic lanehouse with architecture by Lissoni Architettura and Wong and Ouyang, and neighbourhood of Dazhongli, ‘zhong’ meaning ‘middle’ in Chinese. relax in one of our many outdoor spaces or terraces, all radiating the urban sophistication of cosmopolitan Shanghai. From the moment you enter, your stay will become an experience. At The Middle House, we believe in intimate luxury, delivered with The Middle House is the sixth hotel in Asia from Swire Hotels and highly personalised service. Whether it's in one of our 111 modern the fourth property from The House Collective. As we travel to new studios or in The Middle House Residences, our collection of 102 destinations, we hope you’ll join us on the journey. THE ROOMS The Middle House offers five types of studios Studios Room Features and two suites – all elegant and sophisticated. All rooms have been designed to provide • State-of-the-art sound experience with a serene, luxurious retreat from urban life. Native Union x La Boite Bluetooth speaker A blend of contemporary design plus modern Room sizes start at 50 sqm, and a selection • Complimentary wireless high-speed of the studios can be coupled to offer even reinterpretations of traditional Chinese internet access more spacious options. -

The International Light Rail Magazine
THE INTERNATIONAL LIGHT RAIL MAGAZINE www.lrta.org www.tautonline.com FEBRUARY 2020 NO. 986 2020 VISION Our predictions for the new systems due to open this year Hamilton LRT cancellation ‘a betrayal’ Tram & metro: Doha’s double opening China launches 363km of new routes Berlin tramways Added value £4.60 Bringing Germany’s What is your tram capital back together project really worth? European Light Rail Congress TWO days of interactive debates... EIGHT hours of dedicated networking... ONE place to be Ibercaja Patio de la Infanta Zaragoza, Spain 10-11 June The European Light Rail Congress brings together leading opinion-formers and decision-makers from across Europe for two days of debate around the role of technology in the development of sustainable urban travel. With presentations and exhibitions from some of the industry’s most innovative suppliers and service providers, this congress also includes technical visits and over eight hours of networking sessions. 2020 For 2020, we are delighted to be holding the event in the beautiful city of Zaragoza in partnership with Tranvía Zaragoza, Mobility City and the Fundación Ibercaja. Our local partners at Tranvía Zaragoza have arranged a depot tour as part of day one’s activities at the European Light Rail Congress. At the event, attendees will discover the role and future of light rail within a truly intermodal framework. To submit an abstract or to participate, please contact Geoff Butler on +44 (0)1733 367610 or [email protected] +44 (0)1733 367600 @ [email protected] www.mainspring.co.uk MEDIA PARTNERS EU Light Rail Driving innovation CONTENTS The official journal of the Light Rail 64 Transit Association FEBRUARY 2020 Vol. -
Global Transmission Report
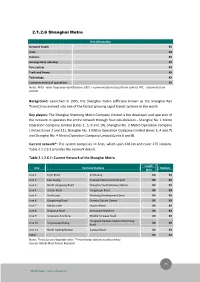
2.1.2.6 Shanghai Metro Key Information Network length XX Lines XX Stations XX Average daily ridership XX Fare system XX Track and Power XX Technology XX Commencement of operations XX Notes: RFID - radio-frequency identification; CBTC – communications based train control; ATC - automatic train control Background: Launched in 1995, the Shanghai metro (officially known as the Shanghai Rail Transit) has evolved into one of the fastest growing rapid transit systems in the world. Key players: The Shanghai Shentong Metro Company Limited is the developer and operator of the network. It operates the entire network through four sub-divisions – Shanghai No. 1 Metro Operation Company Limited (Lines 1, 5, 9 and 10), Shanghai No. 2 Metro Operation Company Limited (Lines 2 and 11), Shanghai No. 3 Metro Operation Company Limited (Lines 3, 4 and 7) and Shanghai No. 4 Metro Operation Company Limited (Lines 6 and 8). Current network*: The system comprises 11 lines, which span 420 km and cover 275 stations. Table 2.1.2.6.1 provides the network details. Table 2.1.2.6.1: Current Network of the Shanghai Metro Length Line Terminal Stations Stations (km) Line 1 Fujin Road Xinzhuang XX XX Line 2 East Xujing Pudong International Airport XX XX Line 3 North Jiangyang Road Shanghai South Railway Station XX XX Line 4 Yishan Road Yangshupu Road XX XX Line 5 Xinzhuang Minhang Development Zone XX XX Line 6 Gangcheng Road Oriental Sports Centre XX XX Line 7 Meilan Lake Huamu Road XX XX Line 8 Shiguang Road Aerospace Museum XX XX Line 9 Songjiang Xincheng Middle Yanggao Road XX XX Hongqiao Railway Station/Hanzhong Line 10 Xinjiangwancheng XX XX Road Line 11 North Jiading/Anting Jiangsu Road XX XX Total - - XX XX Notes: *Includes overlapping tracks; **Interchange stations counted twice Source: Global Mass Transit Research 44 Global Mass Transit Research Ridership: In 2010, the system carried 1.9 billion passengers, translating into an average daily ridership of 5.2 million passengers. -

Identifying Organizational and Contractual Drivers Behind Metro Accidents in Shanghai
IDENTIFYING ORGANIZATIONAL AND CONTRACTUAL DRIVERS BEHIND METRO ACCIDENTS IN SHANGHAI Yue Chen, 4181166 Construction Management and Engineering Faulty of Civil Engineering Technology University of Delft November 2013 0 ABSTRACT In recent years, China has witnessed rapid development in urban transportation, especially in metro projects. However the safety records of metro projects is rather worrying and cannot help to make us think where actually is going wrong. Official reports have claimed that the causes for those metro accidents are mainly from technical and organizational aspects. But are the reports really telling the true story? Or are there deeper reasons that lead to accidents which are not so obvious? In previous studies, Martin de Jong and Yongchi Ma have asked the same question. They conduct their research on three Chinese cities of Beijing, Hangzhou and Dalian through Jens Rasmussen’s safety theory: drift to safety boundaries. In this theory, various incentives drive stakeholders to trade off quality and safety for other core values, resulting in safety boundaries to be crossed. All three cities represent a certain extent of profit driven, excessive subcontracting and loose monitoring which rightly match what is described in Rasmussen’s theory. In my study, I will take the city Shanghai as an example to do a replicative research following Martin de Jong and Ma Yongchi’s work. Based on the main research question of searching for the contractual and organizational arrangements in metro accidents, firstly Rasmussen’s theory will be discussed in Chapter 2 to lay a theoretical underpinning for latter research. Secondly the development of Shanghai metro system will be introduced to provide background information for latter case studies. -
Shanghai Hongqiao Railway Station 上海虹桥火车站 / Shenhong Road, Minhang District, Shanghai 上海
Shanghai Hongqiao Railway Station 上海虹桥火车站 / Shenhong Road, Minhang District, Shanghai 上海 市闵行区申虹路 (86-021-51245555) Quick Guide General Information Board the Train / Leave the Station Transportation Station Details Station Map Useful Sentences General Information Shanghai Hongqiao Railway Station, opened on July 1, 2010, is located in Minhang District, west of Shanghai City Center. It is one of the four major railway stations of Shanghai. It is the junction of Shanghai–Hangzhou High-Speed Railway, Shanghai–Ningbo High-Speed Railway, and Shanghai–Beijing High-Speed Railway. With an area of 1.3 million square meters, Shanghai Hongqiao Railway Station is the largest railway station in Asia. It is situated west of Shanghai Hongqiao International Airport, only a subway stop away from Terminal, serving as a major part of the Hongqiao Comprehensive Transportation Hub. Board the Train / Leave the Station Boarding progress at Shanghai Hongqiao Railway Station: The square of Shanghai Hongqiao Railway Station Ticket Office (售票处) at the, both squares have ticket offices Entrance and security check (also with tickets and travel documents) Get onto the departure level on F2 by elevator Buy tickets (with your travel documents) Pick up tickets (with your travel documents and booking number) Find your own waiting room according to the LED screen or your tickets Wait for check-in Have tickets checked and take your luggage TOP Walk through the passage and find your boarding platform Board the train and find your seat Leaving Shanghai Hongqiao Railway Station: The B1 level, aka the arrival level, is where all the trains are pulled off. Each train has its own exit tunnel. -

2019-Shanghai Basic Facts
SHANGHAI BASIC FACTS 2019 Editorial Board Adviser: Zhou Huilin, Zhu Yonglei Editors-in-Chief: Xu Wei, Zhou Ya, Tang Huihao Deputy Editors-in-Chief: Yin Xin, Chen Yongqi, Qian Fei Editor: Cao Meifang SHANGHAI BASIC FACTS 2019 Compiled by: Information Office of Shanghai Municipality Shanghai Municipal Statistics Bureau ZHONGXI BOOK COMPANY SHANGHAI Located at the estuary of the Yangtze River in eastern China and facing the Pacific Ocean, Shanghai sprawls across an area of over 6,340.5 square kilometers with a population of 24.2378 million in 2018. Shanghai is China’s most thriving economic center, with GDP per capita climbing to US$20,398 by the end of 2018. Shanghai is a pioneer in China’s reform and opening- up, as well as innovation. A total of 670 multinational enterprises have set up regional headquarters in the city, and 441 foreign- invested R&D centers have also been established here. Shanghai is one of the world’s financial centers with its financial markets generating a total transaction volume of 1,645.78 trillion yuan and trading volumes of several products ranked top among global markets. An RMB products center, which matches the currency’s international status, has taken form in the city. Shanghai is an important shipping center, handling 730.4794 million tons of goods in 2018. On top of that, its international container volume reached 42.0102 million TEUs, the highest in the world for nine straight years. When it comes to the number of cruise ship passengers, the city ranked fourth in the world. Some 771,600 flights were processed at Shanghai Pudong and Hongqiao international airports, reaching 117.6343 million inbound and outbound trips. -

CNY and Valentine's Day 2016
For immediate release The Sukhothai Shanghai’s URBAN Lounge Presents premium gins from around the world in a buzzing venue (Shanghai, China) Located in the stylish lobby of The Sukhothai Shanghai is URBAN Lounge, offering a carefully curated collection of premium gins and tonics from around the world, a trolley of fresh herbs and delectable light nibbles. This lively venue is the perfect place to unwind and socialise in the heart of Jing’an district. Featuring cool, clean-cut lines and minimal furnishings to exude timeless elegance, URBAN Lounge provides a relaxing setting for afternoon tea, quick gatherings and casual business meetings. The 12-metre long teakwood bar spanning across the lounge is the highlight of the restaurant, with natural walnut wood, glowing bronze and textured stones all add to the ambience, finished by abstract paintings to give a warm atmosphere. URBAN Lounge stocks a gallery of over 200 global gins and premium tonics to take the enjoyment of this classic highball to new heights. With a cherry-picked selection of garnishes on display on the specially-designed cocktail trolley, guests may explore different flavour profiles and personalise the drink with their favourite garnish to harmonise or create a contrast to the gin's key flavours. Page 2 URBAN Lounge - Presents premium gins from around the world in a buzzing venue The signature herb trolley is a wellness alternative, featuring 29 specialty tea blends and over 8 organic herbs. Guests may create their own concoctions by choosing their own combination of herbs in freshly-infused drinks. Freshly-cut herbs are rinsed in iced water to concentrate the fragrances, and brewed in boiling water to release the aromas into the drink. -

German Centre for Industry and Trade Shanghai Co. Ltd. 88 Keyuan Road
German Centre for Industry and Trade Shanghai Co. Ltd. 88 Keyuan Road, Zhangjiang Hi-Tech Park Pudong, 201203 Shanghai, China Phone: +86 21 2898 6888 www.germancentreshanghai.com Line 11 North Jiading Line 7 Meilian Lake West Jiading Line 1 Luonan Xincun Fujin Rd. Line 3 Baiyin Rd. Panguang Road Jiangyang Youyi Rd.(W) Rd. (N) Shanghai Circuit Liuhang Tieli Rd. Bao‘an Highway Changji Rd. (E) Jiading Xincheng Youyi Rd. Line 11 Gucun Park Jinqiu Rd. Malu Baoyang Rd. Guofan Rd. Shuangjiang Rd. West Gaoqiao Gongfu Xincun Gaoqiao Qihua Rd. Chenxianggong Rd. Shuichan Rd. Fengxiang Rd. Shanghai Huaqiao Anting Shanghai Nanxiang University Hulan Rd. Zhaofeng Rd. Automobile City Songbing Rd. Line 10 Guangming Rd. Nanchen Rd. Taopu Xincun Nanda Rd. Zhanghuabang Tonghe Xincun Gangcheng Rd. Jilong Rd. Shangda Rd. Xinjiang Songfa Rd. Wancheng Qi‘an Rd. Wuwei Rd. Gongkang Rd. Line 8 Line 6 Changjiang Yin‘gao Rd. (E) Waigaoqiao Changzhong Rd. Rd. (S) Shiguang Rd. Free Trade Zone (N) Qilianshan Rd. Gulang Rd. Pengpu Xincun Yingao Rd. (S) Sanmen Rd. Dachang Town Liziyuan Tongchuan Rd. Wuwei Rd. (E) Nenjiang Rd. Hangjin Rd. Jiangwan Jiangwan Stadium Circus ShanghaiWorld Wenshui Rd. West Shanghai Town Dahuasan Rd. Xingzhi Rd. Railway station Waigaoqiao Xincun Rd. Chifeng Dabaishu Wujiaochang Free Trade Zone (S) Yanchang Rd. Xiangyin Rd. Meiling Jinyun Rd.JinshajiangFengzhuang Rd. (W) Football Stadium Rd. Rd. (N) Zhenru Langao Rd. Zhouhai Rd. Hongkou Guoquan Rd. Line 13 Xizang Zhongshan Rd. (N) Caoyang Huangxing Park Rd. Quyang Rd. Wuzhou Ave. Fengqiao Zhongxing Dongbaoxing Tongji University Rd. Rd. (N) Qilianshan Siping Rd. Zhengping Rd. -

HOUSING PRICE, DISTRICTS, and TRANSPORTATION INFRASTRUCTURE: a STUDY of PRICE SPILLOVER in SHANGHAI by GVAR METHOD by Changqin
HOUSING PRICE, DISTRICTS, AND TRANSPORTATION INFRASTRUCTURE: A STUDY OF PRICE SPILLOVER IN SHANGHAI BY GVAR METHOD by Changqing Mu A dissertation submitted to the Faculty of the University of Delaware in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Economics Spring 2017 © 2017 Changqing Mu All Rights Reserved HOUSING PRICE, DISTRICTS, AND TRANSPORTATION INFRASTRUCTURE: A STUDY OF PRICE SPILLOVER IN SHANGHAI BY GVAR METHOD by Changqing Mu Approved: __________________________________________________________ James L. Butkiewicz, Ph.D. Chair of the Department of Economics Approved: __________________________________________________________ Bruce W. Weber, Ph.D. Dean of the College of Business and Economics Approved: __________________________________________________________ Ann L. Ardis, Ph.D. Senior Vice Provost for Graduate and Professional Education I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ Siyan Wang, Ph.D. Professor in charge of dissertation I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ James L. Butkiewicz, Ph.D. Member of dissertation committee I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. Signed: __________________________________________________________ William R. Latham III, Ph.D. Member of dissertation committee I certify that I have read this dissertation and that in my opinion it meets the academic and professional standard required by the University as a dissertation for the degree of Doctor of Philosophy. -

Attachment a Page 1 of 5
Attachment A Page 1 of 5 Attachment O-RUS Non-Levelized Generic page 1 of 5 Formula Rate - Non-Levelized Rate Formula Template For the 12 months ended 12/31/13 Utilizing RUS Form 12 Data Arkansas Electric Cooperative Corporation Line Allocated No. Amount 1 GROSS REVENUE REQUIREMENT (page 3, line 31) $ 1,518,687 REVENUE CREDITS (Note T) Total Allocator 2 Account No. 454 (page 4, line 30) 0 TP 0.07515 0 3 Account No. 456 (page 4, line 33) 0 TP 0.07515 0 4 Revenues from Grandfathered Interzonal Transactions 0 TP 0.07515 0 5 Revenues from service provided by the ISO at a discount 0 TP 0.07515 0 6 TOTAL REVENUE CREDITS (sum lines 2-5) 0 7 NET REVENUE REQUIREMENT (line 1 minus line 6) $ 1,518,687 DIVISOR 8 Average of 12 coincident system peaks for requirements (RQ) service (Note A) 200,176 9 Plus 12 CP of firm bundled sales over one year not in line 8 (Note B) 0 10 Plus 12 CP of Network Load not in line 8 (Note C) 0 11 Less 12 CP of firm P-T-P over one year (enter negative) (Note D) 0 12 Plus Contract Demand of firm P-T-P over one year 0 13 Less Contract Demand from Grandfathered Interzonal transactions over one year (enter negative) (Note S) 0 14 Less 12 CP or Contract Demands from service over one year provided by ISO at a discount (enter negative) 0 15 Divisor (sum lines 8-14) 200,176 16 Annual Cost ($/kW/Yr) (line 7 / line 15) 7.587 17 Network & P-to-P Rate ($/kW/Mo) (line 16 / 12) 0.632 Peak Rate Off-Peak Rate 18 Point-To-Point Rate ($/kW/Wk) (line 16 / 52; line 16 / 52) 0.146 $0.146 19 Point-To-Point Rate ($/kW/Day) (line 16 / 260; line