Marlana Dugger
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fictional Illustration Language with Reference to MC Escher and Istvan
New Trends and Issues Proceedings on Humanities and Social Sciences Volume 4, Issue 11, (2017) 156-163 ISSN : 2547-881 www.prosoc.eu Selected Paper of 6th World Conference on Design and Arts (WCDA 2017), 29 June – 01 July 2017, University of Zagreb, Zagreb – Croatia Fictional Illustration Language with Reference to M. C. Escher and Istvan Orosz Examples Banu Bulduk Turkmen a*, Faculty of Fine Arts, Department of Graphics, Hacettepe University, Ankara 06800, Turkey Suggested Citation: Turkmen, B. B. (2017). Fictional illustration language with reference to M. C. Escher and Istvan Orosz examples. New Trends and Issues Proceedings on Humanities and Social Sciences. [Online]. 4(11), 156-163. Available from: www.prosoc.eu Selection and peer review under responsibility of Prof. Dr. Ayse Cakır Ilhan, Ankara University, Turkey. ©2017 SciencePark Research, Organization & Counseling. All rights reserved. Abstract Alternative approaches in illustration language have constantly been developing in terms of material and technical aspects. Illustration languages also differ in terms of semantics and form. Differences in formal expressions for increasing the effect of the subject on the audience lead to diversity in the illustrations. M. C. Escher’s three-dimensional images to be perceived in a two-dimensional environment, together with mathematical and symmetry-oriented studies and the systematic formed by a numerical structure in its background, are associated with the notion of illustration in terms of fictional meaning. Istvan Orosz used the technique of anamorphosis and made it possible for people to see their perception abilities and visual perception sensitivities in different environments created by him. This study identifies new approaches and illustration languages based on the works of both artists, bringing an alternative proposition to illustration languages in terms of systematic sub-structure and fictional idea sketches. -

The George-Anne Student Media
Georgia Southern University Digital Commons@Georgia Southern The George-Anne Student Media 10-27-2003 The George-Anne Georgia Southern University Follow this and additional works at: https://digitalcommons.georgiasouthern.edu/george-anne Part of the Higher Education Commons Recommended Citation Georgia Southern University, "The George-Anne" (2003). The George-Anne. 3032. https://digitalcommons.georgiasouthern.edu/george-anne/3032 This newspaper is brought to you for free and open access by the Student Media at Digital Commons@Georgia Southern. It has been accepted for inclusion in The George-Anne by an authorized administrator of Digital Commons@Georgia Southern. For more information, please contact [email protected]. ^^H ■■■^^■■i ^^^mm HB^^BHHH 1 •.siannsnc Covering the campus like a swarm of gnats I he (Mficial Student Newspaper of Georgi iniversit Volleyball wins trio of matches to stay perfect at home SPORTS ^ Page 6 NEWS More on the events www.stp.georgiasouthern.edu that shaped Homecoming 2003 Page 9 or * or et THE END 11- 4 ■ J OF AN ERA By Eli Boorstein [email protected] Iff s the old adage says, "All good things must come I to an end." 7 The only problem is, that phrase is not supposed > » i to apply to Georgia Southern. The No. 19 Eagle football team, after storming back to take the lead, saw The Citadel respond late to win 28-24, spoiling Homecoming festivities at Paul- son Stadium Saturday afternoon. :ss With the loss, their fourth of the season, the Ea- • gles' streak of six straight postseason berths will likely :ss be coming to an end. -

Some Common Themes in Visual Mathematical Art
BRIDGES Mathematical Connections in Art, Music, and Science Some Common Themes in Visual Mathematical Art Robert W. Fathauer Tessellations Company Tempe, AZ 85281, USA E-mail: [email protected] Abstract Mathematics and art are two seemingly disparate fields according to contemporary views, but there are a number of visual artists who make mathematics a focus of their work. There are several themes that have been widely used by mathematical artists. These include polyhedra, tessellations, impossible figures, MObius bands, distorted or unusual perspective systems, and fractals. Descriptions and examples are provided in this paper, which is intended to some degree as an fntroduction to the Exhibit of Visual Mathematical Art held as part of Bridges 2001. 1. Introduction Historically, mathematics has played an important role in visual art, particularly in perspective drawing; i.e., the means by which a three-dimensional scene is rendered convincingly on a flat canvas or piece of paper. Mathematics and art are two seemingly disparate fields according to contemporary views, the first often considered analytical and the second emotional. Mathematics does not play an overt role in most contemporary art, and in fact, many artists seldom or never employ even -perspective drawing. However, there are a number of contemporary visual artists who make mathematics a focus of their work. Several notable figures in history paved the way for these individuals. There are obviously no rules or limits on themes and ideas in mathematical art. However, there are a number of themes that have been widely used by mathematical artists. Some of these are described here, with examples. -

Estimular El Crecimiento De Bacterias Para Mejorar Los
BIOLOGÍA Los investigadores vieron el cambio de contar con los dedos Los hallazgos permiten un soporte empírico más fuerte para la en el momento de empezar a basarse en la memoria cuando existencia de teorías sobre el desarrollo de las matemáticas, en repitieron el experimento un año después con los niños. En palabras de Jessica Cantlon, neurocientífica cognitiva en la esta segunda vez, los niños contaban menos con los dedos y Universidad de Rochester, en Nueva York. Pero añade que: “no APRENDIENDO A SUMAR hacían menos movimientos labiales (como contando en voz sabemos qué información es la que pasa entre el hipocampo alta) que la primera vez. Para poder saber qué pasa realmen- y el neocórtex”. Una manera de demostrar esta cuestión sería DE CABEZA: ¿QUÉ OCURRE te en el cerebro mientras se efectúa una tarea así, se recurrió extender el estudio a niños con el hipocampo dañado o con a la imagen por resonancia magnética funcional (FMRI, por alguna discapacidad en el aprendizaje de las matemáticas. EN EL CEREBRO? sus siglas en inglés). Básicamente, con esta técnica se puede Por Cristóbal Rodero ver qué zonas del cerebro se utilizan más en un determinado Menon sugiere que la maduración del hipocampo y sus conexio- momento en función de la cantidad de sangre que llegue, y nes esconden probablemente no solo el desarrollo de habilida- Recuerdo que en el colegio, para sumar primero me enseñaron en el caso del experimento que estamos comentando, el ele- des matemáticas basadas en la memoria, sino también algún otro con objetos físicos, de ahí a escribir palitos en el papel, lue- gido fue el hipocampo. -
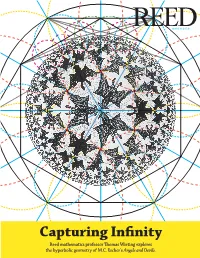
Capturing Infinity Reed Mathematics Professor Thomas Wieting Explores the Hyperbolic Geometry of M.C
‰march 2010 Capturing Infinity Reed mathematics professor Thomas Wieting explores the hyperbolic geometry of M.C. Escher’s Angels and Devils. Capturing Infinity The Circle Limit Series of M.C. Escher BY THOMAS WIETING In July 1960, shortly after his 62nd birthday, the graphic artist M.C. Escher completed Angels and Devils, the fourth (and final) woodcut in his Circle Limit Series. I have a vivid memory of my first view of a print of this astonishing work. Following sensations of surprise and delight, two questions rose in my mind. What is the underlying design? What is the purpose? Of course, within the world of Art, narrowly interpreted, one might regard such questions as irrelevant, even impertinent. However, for this particular work of Escher, it seemed to me that such questions were precisely what the artist intended to excite in my mind. In this essay, I will present answers to the foregoing questions, based upon Escher’s articles and letters and upon his workshop drawings. For the mathematical aspects of the essay, I will require nothing more but certainly nothing less than thoughtful applications of straightedge and compass. The Dutch artist Maurits C. Escher (1898–1972) Escher completed CLIV, also known as Angels and Devils, in 1960. 22 Reed magazine March 2010 Regular Division III (1957) demonstrates Escher’s mastery of tessellation. At the same time, he was dissatisfied with the way the pattern was arbitrarily interrupted at the edges. Day and Night (1938) is the most popular of Escher’s works. Capturing Infinity would not permit what the real materials of In 1959, Escher described, in retrospect, a his work shop required: a finite boundary. -

Drawing Hands. the Themes of Representation in Steinberg and Escher's Images †
Proceedings Drawing Hands. The Themes of Representation in Steinberg and Escher’s Images † Edoardo Dotto Università di Catania, Struttura Didattica Speciale di Architettura, 96100 Siracusa, Italy; [email protected] † Presented at the International and Interdisciplinary Conference IMMAGINI? Image and Imagination between Representation, Communication, Education and Psychology, Brixen, Italy, 27–28 November 2017. Published: 24 November 2017 Abstract: Despite the obvious differences between the work of Dutch graphic artist M.C. Escher and that of Romanian draftsman S. Steinberg, with a closer look is possible to trace strong affinities between some of their works and many of the themes they handled, such as the drawing of metamorphoses, the figure-background relationship, and the intercourse between reality and representation space. In spite of a general mood difference between their respective graphic narrations, the work of the two authors appears to be based on the same kind of anxieties that have crossed the twentieth century, involving different fields of knowledge. Keywords: impossible figures; incompleteness theorems; Escher; Steinberg 1. Introduction Few draftsmen, among the graphic artists of the twentieth century, may appear as distant as Maurits Cornelis Escher (Figure 1) and Saul Steinberg (Figure 2). Steinberg has built his own career as a humorist, developing, since years of collaboration with the Milanese magazine Il Bertoldo, to the mature works on New Yorker’s pages, a caustic, fulminant, sometimes even moving spirit. Escher, devoted to a lonely and coherent search work on certain precise themes—from the regular division of the plane to the anamorphosis–, was perceived as “the absurd draftsmen”, appreciated by mathematicians and crystallographers for the precision with which, by applying complex geometric principles, has managed to shape the images that are often described paradoxically and imaginatively. -

The Kaiser Panorama
r*..-r 3-0 lmaaina Past & Present A Publ~cationof National Stereoscopic Association, Inc. The Kaiser Panorama *; *; 9..* zu -2' . Shooting SanLFrancisc in 3-0 from a ~efic>fer~ byM.rLWllllrc elcome to the first install- ment of Pi@ Flawmi Finds. WNot long after I started shooting stereo images, I rew that I could combine my love of stereo photography with my fond- ness for 1950s-era styling, design and decor by collecting amateur stereo slides that were shot in the "golden age" of the Stereo Real- ist-the late 1940s through the early 1960s. These slides sometimes contain priceless images of wery- day life in that era, and the fact that they are 3-D and were often recorded on Kodachrome film.-- I whose colors today seem as fr&h Whotcouldkbatarfiw~hthc195Ostha,apWtfl#kcdbrr?A##nntly as the day the photo was taken, takmota0,~tm&thls~kkkkdonEya1953.'~#maynotk~- makes viewing these slides the i&inthe~hrre,a~s#kvicwarnncaJsmorrngcflodtcdtmasdf next best thing to hopping aboard behindthemwrmnf &olMieveistkwifeoftkphotogrPpha. 7bissWisinanoMer- a time machine! From clothing style(gmywith~cdgcJ)K~m~mocnrt.OdhasiDdafrwntksomc and hairstyles to home decor to photogmpher indude many scenes in and oround his home in Portknd, Ongon. Many of modes of transportation, these theman?bbckdwiththe~tnet~~sooutof~~IkcaadthehomeandckOW frozen moments of time show byit. Aportfrom ~~t-daykukof~~~bsdsand~its what things were really like in the ext&harctxlngrdNtbkfnnnthcwy#c#PraradhtkrrYdanca3,5O~cyp. ..........................." .... "..... ........ "" middle of the twentieth century. While collections of these ama- teur slides are interesting to view, exploring them often requires sifting through numerous shots marred by focus or exposure prob- lems, distant subjects containing minimal depth, or generic scenery that would look the same today as it did 50 years ago. -

An Introspective Look at the Use of Art in Teaching Geometry Elizabeth Heskett
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Eastern Michigan University: Digital Commons@EMU Eastern Michigan University DigitalCommons@EMU Senior Honors Theses Honors College 2007 Thinking Outside the Box: An Introspective Look at the Use of Art in Teaching Geometry Elizabeth Heskett Follow this and additional works at: http://commons.emich.edu/honors Part of the Science and Mathematics Education Commons Recommended Citation Heskett, Elizabeth, "Thinking Outside the Box: An Introspective Look at the Use of Art in Teaching Geometry" (2007). Senior Honors Theses. 155. http://commons.emich.edu/honors/155 This Open Access Senior Honors Thesis is brought to you for free and open access by the Honors College at DigitalCommons@EMU. It has been accepted for inclusion in Senior Honors Theses by an authorized administrator of DigitalCommons@EMU. For more information, please contact lib- [email protected]. Thinking Outside the Box: An Introspective Look at the Use of Art in Teaching Geometry Abstract Geometry is typically thought of as a discipline in mathematics that is taught using formulas and basic shapes, but this idea is only the beginning. Geometry can be combined with art to enhance mathematical lessons for students. Educators must realize that visual representations of different mathematical concepts are a wonderful way to teach children geometry in a meaningful way. The f“ undamental notion that integrating the arts into one’s teaching can help facilitate learning in the mathematics classroom, as the arts can recapture the wonder of learning mathematics. The onnec ction between instruction and imagination is bridged and learning becomes play, and play becomes learning” (Muller and Ward 22). -

TOPICS on ENVIRONMENTAL and PHYSICAL GEODESY Compiled By
TOPICS ON ENVIRONMENTAL AND PHYSICAL GEODESY Compiled by Jose M. Redondo Dept. Fisica Aplicada UPC, Barcelona Tech. November 2014 Contents 1 Vector calculus identities 1 1.1 Operator notations ........................................... 1 1.1.1 Gradient ............................................ 1 1.1.2 Divergence .......................................... 1 1.1.3 Curl .............................................. 1 1.1.4 Laplacian ........................................... 1 1.1.5 Special notations ....................................... 1 1.2 Properties ............................................... 2 1.2.1 Distributive properties .................................... 2 1.2.2 Product rule for the gradient ................................. 2 1.2.3 Product of a scalar and a vector ................................ 2 1.2.4 Quotient rule ......................................... 2 1.2.5 Chain rule ........................................... 2 1.2.6 Vector dot product ...................................... 2 1.2.7 Vector cross product ..................................... 2 1.3 Second derivatives ........................................... 2 1.3.1 Curl of the gradient ...................................... 2 1.3.2 Divergence of the curl ..................................... 2 1.3.3 Divergence of the gradient .................................. 2 1.3.4 Curl of the curl ........................................ 3 1.4 Summary of important identities ................................... 3 1.4.1 Addition and multiplication ................................. -

Download PDF File
“Matters of Consequence is a master work in applying evolutionary understanding to the critical problems of our time and revealing a design of action to carry humanity through to the next stage of our development. I highly recommend it.” Barbara Marx Hubbard, futurist, author of Emergence and Conscious Evolu- tion, and founder of the Foundation for Conscious Evolution. “Copthorne Macdonald has written an utterly splendid review and analysis of what is really important in life. Its particular value is its focus on what we most need to attend to about our emerging world. He has organized his book well, with sharp, incisive comments. Matters of Consequence shows us our own human faces with real gems of insight. I finally found myself creating a new file called ‘Cop’s Gems.’ Get it. You need it.” Paul H. Ray, co-author of The Cultural Creatives and author of The Integral Cul- ture Survey, books that report on his extensive studies of the lifestyles, interests, values, expectations, preferences, and choices of Americans. “Herein you’ll find a guided tour of the inner and outer landscape an educated, compassionate and engaged citizen needs to inhabit to gen- erate a rich future worth living into. This book is brilliant yet accessi- ble, terse yet so deeply considered that each paragraph opens worlds. One of Macdonald’s greatest gifts is the section where he evokes a plausible and pleasing vision for 2050 and then tells us the intelligent steps we could take now to get there. Matters of Consequence is a good read and a lasting resource.” Vicki Robin, co-author of Your Money or Your Life. -

Planets of Peril
FFOORRGGOOTTTTEENN FFUUTTUURREESS XXII:: RROOLLEE--PPLLAAYYIINNGG IINN TTHHEE WWOORRLLDDSS OOFF SSTTAANNLLEEYY GG.. WWEEIINNBBAAUUMM’’SS 11993300SS SSCCIIEENNCCEE FFIICCTTIIOONN BBYY MMAARRCCUUSS LL.. RROOWWLLAANNDD FORGOTTEN FUTURES XI: PLANETS OF PERIL ROLE-PLAYING IN THE WORLDS OF STANLEY G. WEINBAUM’S 1930S SCIENCE FICTION BY MARCUS L. ROWLAND GAMES MATERIAL AND MOST ILLUSTRATIONS COPYRIGHT © MARCUS L. ROWLAND 2010 To the best of my knowledge and belief all European copyright in the works of Stanley Weinbaum accompanying this collection, including editorial copyright, has now expired. No copyright in these works is claimed by the current editor. About half of this material was originally scanned by Malcolm Farmer for Project Gutenberg Australia, the remainder by me for this collection and for general publication on line. While every effort has been made to remove OCR and other errors it is likely that some remain. Some obvious proofreading and editorial errors found in the original books (such as two variant spellings of the hero’s surname in The Black Flame) have been corrected. I have not tried to convert American English to British English! Special thanks to Malcolm Farmer for his help with proofreading etc. Several stories could not be included since they remain in European copyright, or their European copyright status is unclear – most can be found on line in the USA or Australia. See end notes for full details. This game contains numerous “spoilers” for Weinbaum’s stories; you are strongly advised to read the fiction first! Print formatting: If you print double-sided, for best results print the cover and this page single sided, and all remaining pages (starting with the contents) double sided. -

Maths and Art: the Whistlestop Tour
Maths and art: the whistlestop tour © 1997−2004, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non−commercial use. For other uses, including electronic redistribution, please contact us. January 2005 Features Maths and art: the whistlestop tour by Lewis Dartnell The world around us is full of relationships, rhythms, correlations, patterns. And mathematics underlies all of these, and can be used to predict future outcomes. Our brains have evolved to survive in this world: to analyse the information it receives through our senses and spot patterns in the complexity around us. In fact, it's thought that the mathematical structure embedded in the rhythm and melody of music is what our brains latch on to, and that this is why we enjoy listening to it. It is perhaps not surprising then that there is a great deal of overlap between mathematics and the art that our brain finds so pleasing to look at. This article is a whistle−stop tour of some of the types of art with a strong mathematical component, or conversely where a mathematical visualisation has an astonishing beauty. Geometric patterns Maths and art: the whistlestop tour 1 Maths and art: the whistlestop tour The "Flower of Life" pattern Simple arrangements of mathematical figures, like circles and triangles, have been extensively used in decoration throughout history. For example, the "Flower of Life" can be seen on the Temple of Osiris at Abydos, Egypt, which dates back about 5,000 years. This pattern, as seen to the right, consists of an array of circles positioned in rows, each one centred on the circumference of circles in the neighbouring rows.