DOCSLIB.ORG

Total Variation and Euler's Elastica for Supervised Learning

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Total Variation and Euler's Elastica for Supervised Learning Total Variation and Euler's Elastica for Supervised Learning Tong Lin [email protected] Hanlin Xue [email protected] Ling Wang* [email protected] Hongbin Zha [email protected] The Key Laboratory of Machine Perception (Ministry of Education), Peking University, Beijing, China *LTCI, T´el´ecomParisTech, Paris, France Abstract Euler Elastica decision boundary In recent years, total variation (TV) and Eu- 1 ler's elastica (EE) have been successfully ap- 0.8 0.6 plied to image processing tasks such as de- 0.4 noising and inpainting. This paper inves- 0.2 tigates how to extend TV and EE to the 0 supervised learning settings on high dimen- 0 0.2 0.4 0.6 0.8 1 sional data. The supervised learning problem can be formulated as an energy functional Figure 1. Results on two moon data by the EE classifier: minimization under Tikhonov regularization (Left) decision boundary; (Right) learned target function. scheme, where the energy is composed of a squared loss and a total variation smooth- ing (or Euler's elastica smoothing). Its so- prehensive empirical comparison of these methods in lution via variational principles leads to an (Caruana & Niculescu-Mizil, 2006)). Existing meth- Euler-Lagrange PDE. However, the PDE is ods can be roughly divided into statistics based and always high-dimensional and cannot be di- function learning based (Kotsiantis et al., 2006). One rectly solved by common methods. Instead, advantage of function learning methods is that pow- radial basis functions are utilized to approxi- erful mathematical theories in functional analysis can mate the target function, reducing the prob- be utilized rather than doing optimizations on discrete lem to finding the linear coefficients of basis data points. functions. We apply the proposed methods to supervised learning tasks (including binary Most function learning methods can be derived from classification, multi-class classification, and Tikhonov regularization, which minimizes a loss term regression) on benchmark data sets. Exten- plus a smoothing regularizer. The most successful sive experiments have demonstrated promis- classification and regression method is SVM (Bishop, ing results of the proposed methods. 2006; Hastie T., 2009; Shawe-Taylor & Cristianini, 2000), whose cost function is composed of a hinge loss and a RKHS norm determined by a kernel. Re- 1. Introduction placing the hinge loss by a squared loss, the modified algorithm is called Regularized Least Squares (RLS) Supervised learning (Bishop, 2006; Hastie T., 2009) in- method (Rifkin, 2002). In addition, manifold regu- fers a function that maps inputs to desired outputs larization (Belkin et al., 2006) introduced a regular- under the guidance of training data. Two main tasks izer of squared gradient magnitude on manifolds. Its in supervised learning are classification and regres- discrete version amounts to graph Laplacian regular- sion. A huge number of supervised learning methods ization (Nadler et al., 2009; Zhou & Sch¨olkopf, 2005), have been developed in several decades (see a com- which approximates the original energy functional. A most recent work is the geometric level set (GLS) Appearing in Proceedings of the 29 th International Confer- classifier (Varshney & Willsky, 2010), with an energy ence on Machine Learning, Edinburgh, Scotland, UK, 2012. functional composed of a margin-based loss and a ge- Copyright 2012 by the author(s)/owner(s). ometric regularization term based on the surface area Total Variation and Euler's Elastica for Supervised Learning of the decision boundary. Experiments showed that Simply, it is a measure of the total quantity of the GLS is competitive with SVM and other state-of-the- change of a function. Notice that if f 0(x) > 0; x 2 art classifiers. [a; b], it is exactly f(b) − f(a) by the basic theorem of calculus. Total variation has been widely used for im- In this paper, the supervised learning problem is for- age processing tasks such as denoising and inpainting. mulated as an energy functional minimization un- The pioneering work is Rudin, Osher, and Fatemi's der Tikhonov regularization scheme, with the en- image denoising model (Rudin et al., 1992): ergy composed of a squared loss and a total varia- Z tion (TV) penalty or an Euler's elastica (EE) penalty. 2 J = ((I − I0) + λjrIj)dx; Since the TV and EE models have achieved great Ω success in image denoising and image inpainting (Aubert & Kornprobst, 2006; Barbero & Sra, 2011; where I0 is the input image with noise, I the desired Chan & Shen, 2005), a natural question is whether the output image, λ a regulation parameter that balances success of TV and EE models on image processing ap- two terms, and Ω a 2D image domain. The first fitting plications can be transferred to high dimensional data term measures the fidelity to the input, while the sec- analysis such as supervised learning. This paper inves- ond is a p-Sobolev regularization term (p = 1) where r tigates the question by extending TV and EE models I is understood in the distributional sense. The main to supervised learning settings, and evaluating their merit is to preserve significant image edges during performance on benchmark data sets against state-of- denoising (Aubert & Kornprobst, 2006; Chan & Shen, the-art methods. Figure 1 shows the classification re- 2005). Note that TV may have different definitions sult on the popular two moon data by the EE clas- (Barbero & Sra, 2011). sifier, and the learned target function. Interestingly, In the machine learning literature, p-Sobolev regular- the GLS classifier (Varshney & Willsky, 2010) is also izer can be found in nonparametric smoothing splines, motivated by image processing techniques, and its gra- generalized additive models, and projection pursuit re- dient descent time marching leads to a mean curvature gression models (Hastie T., 2009). Specifically, Belkin flow. et al. proposed the manifold regularization term Z The paper is organized as follows. We begin with a jr j2 brief review of TV and EE in Section 2. In Section M f dx; x2M 3 the proposed models are described, and numerical solutions are developed in Section 4. Section 5 presents on a manifold M (Belkin et al., 2006). On the other the experimental results, and Section 6 concludes this hand, discrete graph Laplacian regularization was dis- paper. cussed in (Zhou & Sch¨olkopf, 2005) as X p jrvfj ; 2. Preliminaries v2V We briefly introduce total variation and Euler's elas- where v is a vertex from V , and p is an arbitrary num- tica from an image processing perspective, and point ber. This penalty measures the roughness of f over a out connections with prior work in the machine learn- graph. ing literature. 2.2. Euler's Elastica (EE) 2.1. Total Variation (TV) Euler (1744) first introduced the elastica energy for The total variation of a 1D real-valued function f is a curve on modeling torsion-free elastic rods. Then defined as Mumford (Mumford, 1991) reintroduced elastica into computer vision. Later, elastica based image inpaint- − nXp 1 ing methods were developed in (Chan et al., 2002; a j − j Vb (f) = sup f(xi+1) f(xi) ; Masnou & Morel, 1998). i=0 A curve γ is said to be Euler's elastica if it is the where the supremum runs over all partitions of given equilibrium curve of the elasticity energy: Z interval [a; b]. If f is differentiable, the total variation 2 can be written as E[γ] = (a + bκ )ds; (1) γ Z b where a and b stand for two positive constant weights, a j 0 j Vb (f) = f (x) dx: κ denotes the scalar curvature, and ds is the arc length a Total Variation and Euler's Elastica for Supervised Learning element. Euler obtained the energy in studying the posed in the literature: hinge loss for SVM, squared steady shape of a thin and torsion-free rod under ex- loss for RLS, logistic loss for logistic regression, Huber ternal forces. The curve implies the lowest elastica en- loss, exponential loss, and among others. Throughout ergy, thus getting its name. According to (Mumford, the paper, squared loss is used in all models due to its 1991), the key link between the elastica and image rather simpler differential form. inpainting relies on the the interpolation capability of elastica. That is, elastica can comply to the con- 3.2. Laplacian Regularization (LR) nectivity principle better than total variation. Such kinds of "nonlinear splines", like classical polynomial A commonly used model using squared loss can be splines, are natural tools for completing the missing or written as occluded edges. Xn 2 min (u(xi) − yi) + λS(u): (5) The Euler's elastica based inpainting model was pro- i=1 posed as (Chan & Shen, 2005) Z Z If the RKHS norm is used for the smoothing term, 2 2 the model is called regularized least squares (RLS) J = (I − I0) dx + λ (a + bκ )jrIjdx; (2) ΩnD Ω (Rifkin, 2002). Another natural choice is the squared L -norm of the gradient: S(u) = jruj2, as proposed in where D is the region to be inpainted, Ω the whole 2 (Belkin et al., 2006). Under a continuous setting, we image domain, and κ the curvature of the associated get the following Laplacian regularization (LR) model: level set curve with Z rI − 2 jr j2 κ = r · ( ): (3) JLR[u] = ((u y) + λ u )dx: (6) jrIj Ω By using calculus of variation, its minimization is re- This LR model has been widely used in the image pro- duced to an nonlinear Euler-Lagrange equation. The cessing literatures. Using calculus of variations, the finite difference scheme can be used to give numerical minimization can be reduced to the following Euler- implementation, and experimental results show that Lagrange partial differential equation (PDE) with a the EE based inpainting performs better than its TV natural boundary condition along @Ω: ( version.
Load more

Recommended publications
  • The Total Variation Flow∗
    THE TOTAL VARIATION FLOW∗ Fuensanta Andreu and Jos´eM. Maz´on† Abstract We summarize in this lectures some of our results about the Min- imizing Total Variation Flow, which have been mainly motivated by problems arising in Image Processing. First, we recall the role played by the Total Variation in Image Processing, in particular the varia- tional formulation of the restoration problem. Next we outline some of the tools we need: functions of bounded variation (Section 2), par- ing between measures and bounded functions (Section 3) and gradient flows in Hilbert spaces (Section 4). Section 5 is devoted to the Neu- mann problem for the Total variation Flow. Finally, in Section 6 we study the Cauchy problem for the Total Variation Flow. 1 The Total Variation Flow in Image Pro- cessing We suppose that our image (or data) ud is a function defined on a bounded and piecewise smooth open set D of IRN - typically a rectangle in IR2. Gen- erally, the degradation of the image occurs during image acquisition and can be modeled by a linear and translation invariant blur and additive noise. The equation relating u, the real image, to ud can be written as ud = Ku + n, (1) where K is a convolution operator with impulse response k, i.e., Ku = k ∗ u, and n is an additive white noise of standard deviation σ. In practice, the noise can be considered as Gaussian. ∗Notes from the course given in the Summer School “Calculus of Variations”, Roma, July 4-8, 2005 †Departamento de An´alisis Matem´atico, Universitat de Valencia, 46100 Burjassot (Va- lencia), Spain, [email protected], [email protected] 1 The problem of recovering u from ud is ill-posed.
    [Show full text]
  • 'I Spy': Mike Leigh in the Age of Britpop (A Critical Memoir)
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Glasgow School of Art: RADAR 'I Spy': Mike Leigh in the Age of Britpop (A Critical Memoir) David Sweeney During the Britpop era of the 1990s, the name of Mike Leigh was invoked regularly both by musicians and the journalists who wrote about them. To compare a band or a record to Mike Leigh was to use a form of cultural shorthand that established a shared aesthetic between musician and filmmaker. Often this aesthetic similarity went undiscussed beyond a vague acknowledgement that both parties were interested in 'real life' rather than the escapist fantasies usually associated with popular entertainment. This focus on 'real life' involved exposing the ugly truth of British existence concealed behind drawing room curtains and beneath prim good manners, its 'secrets and lies' as Leigh would later title one of his films. I know this because I was there. Here's how I remember it all: Jarvis Cocker and Abigail's Party To achieve this exposure, both Leigh and the Britpop bands he influenced used a form of 'real world' observation that some critics found intrusive to the extent of voyeurism, particularly when their gaze was directed, as it so often was, at the working class. Jarvis Cocker, lead singer and lyricist of the band Pulp -exemplars, along with Suede and Blur, of Leigh-esque Britpop - described the band's biggest hit, and one of the definitive Britpop songs, 'Common People', as dealing with "a certain voyeurism on the part of the middle classes, a certain romanticism of working class culture and a desire to slum it a bit".
    [Show full text]
  • Total Variation Deconvolution Using Split Bregman
    Published in Image Processing On Line on 2012{07{30. Submitted on 2012{00{00, accepted on 2012{00{00. ISSN 2105{1232 c 2012 IPOL & the authors CC{BY{NC{SA This article is available online with supplementary materials, software, datasets and online demo at http://dx.doi.org/10.5201/ipol.2012.g-tvdc 2014/07/01 v0.5 IPOL article class Total Variation Deconvolution using Split Bregman Pascal Getreuer Yale University ([email protected]) Abstract Deblurring is the inverse problem of restoring an image that has been blurred and possibly corrupted with noise. Deconvolution refers to the case where the blur to be removed is linear and shift-invariant so it may be expressed as a convolution of the image with a point spread function. Convolution corresponds in the Fourier domain to multiplication, and deconvolution is essentially Fourier division. The challenge is that since the multipliers are often small for high frequencies, direct division is unstable and plagued by noise present in the input image. Effective deconvolution requires a balance between frequency recovery and noise suppression. Total variation (TV) regularization is a successful technique for achieving this balance in de- blurring problems. It was introduced to image denoising by Rudin, Osher, and Fatemi [4] and then applied to deconvolution by Rudin and Osher [5]. In this article, we discuss TV-regularized deconvolution with Gaussian noise and its efficient solution using the split Bregman algorithm of Goldstein and Osher [16]. We show a straightforward extension for Laplace or Poisson noise and develop empirical estimates for the optimal value of the regularization parameter λ.
    [Show full text]
  • Guaranteed Deterministic Bounds on the Total Variation Distance Between Univariate Mixtures
    Guaranteed Deterministic Bounds on the Total Variation Distance between Univariate Mixtures Frank Nielsen Ke Sun Sony Computer Science Laboratories, Inc. Data61 Japan Australia [email protected] [email protected] Abstract The total variation distance is a core statistical distance between probability measures that satisfies the metric axioms, with value always falling in [0; 1]. This distance plays a fundamental role in machine learning and signal processing: It is a member of the broader class of f-divergences, and it is related to the probability of error in Bayesian hypothesis testing. Since the total variation distance does not admit closed-form expressions for statistical mixtures (like Gaussian mixture models), one often has to rely in practice on costly numerical integrations or on fast Monte Carlo approximations that however do not guarantee deterministic lower and upper bounds. In this work, we consider two methods for bounding the total variation of univariate mixture models: The first method is based on the information monotonicity property of the total variation to design guaranteed nested deterministic lower bounds. The second method relies on computing the geometric lower and upper envelopes of weighted mixture components to derive deterministic bounds based on density ratio. We demonstrate the tightness of our bounds in a series of experiments on Gaussian, Gamma and Rayleigh mixture models. 1 Introduction 1.1 Total variation and f-divergences Let ( R; ) be a measurable space on the sample space equipped with the Borel σ-algebra [1], and P and QXbe ⊂ twoF probability measures with respective densitiesXp and q with respect to the Lebesgue measure µ.
    [Show full text]
  • Student Lounge Revamped
    The Pride http://www.csusm.edu/pride California State University, San Marcos Vol VIII No. 5/ Tuesday, September 26,2000 Faculty Files Grievance By: Jayne Braman istration and faculty. University's Convocation, Pride Staff The "faculty workload issue" President Gonzalez stated, "We revolves around a grievance filed are a CSU campus and we do have Students have many factors by the San Marcos chapter of to follow system-wide guidelines to consider when deciding on the faculty union, the California and operate within our funding which college to attend. Many Faculty Association (CFA), which formula which is predicated on CSUSM students credit the small is pending arbitration scheduled 15 units per Full Time Equivalent classes, the writing requirement, for October 28. Although the Student (FTES) and 12 Direct and the availability of professors details of the arbitration are not Weighted Teaching Units (WTU) as factors that ultimately add made public, the outcome of this for faculty." value to their education as well hearing will set a precedent that "The faculty argues that fund- as to their degrees. Students have will determine the future direc- ing increases depend strictly on also noted that the reputation tion of faculty workload. FTES, not on faculty teaching 12, of the institution will continue CSUSM President Alexander units," according to Dr. George to influence the value of their Gonzalez explains, "Faculty is Diehr, local union CFA President degrees long after they leave this contracted to work twelve (12) and Professor of Management campus. credit hours per semester." Science. "In fact," Diehr con- The window of opportunity Gonzalez continues, "This labor tends, "there is no mention any- is still wide open for CSUSM contract is part of a collective- where of faculty being required to to decide its future direction.
    [Show full text]
  • Calculus of Variations
    MIT OpenCourseWare http://ocw.mit.edu 16.323 Principles of Optimal Control Spring 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 16.323 Lecture 5 Calculus of Variations • Calculus of Variations • Most books cover this material well, but Kirk Chapter 4 does a particularly nice job. • See here for online reference. x(t) x*+ αδx(1) x*- αδx(1) x* αδx(1) −αδx(1) t t0 tf Figure by MIT OpenCourseWare. Spr 2008 16.323 5–1 Calculus of Variations • Goal: Develop alternative approach to solve general optimization problems for continuous systems – variational calculus – Formal approach will provide new insights for constrained solutions, and a more direct path to the solution for other problems. • Main issue – General control problem, the cost is a function of functions x(t) and u(t). � tf min J = h(x(tf )) + g(x(t), u(t), t)) dt t0 subject to x˙ = f(x, u, t) x(t0), t0 given m(x(tf ), tf ) = 0 – Call J(x(t), u(t)) a functional. • Need to investigate how to find the optimal values of a functional. – For a function, we found the gradient, and set it to zero to find the stationary points, and then investigated the higher order derivatives to determine if it is a maximum or minimum. – Will investigate something similar for functionals. June 18, 2008 Spr 2008 16.323 5–2 • Maximum and Minimum of a Function – A function f(x) has a local minimum at x� if f(x) ≥ f(x �) for all admissible x in �x − x�� ≤ � – Minimum can occur at (i) stationary point, (ii) at a boundary, or (iii) a point of discontinuous derivative.
    [Show full text]
  • Calculus of Variations in Image Processing
    Calculus of variations in image processing Jean-François Aujol CMLA, ENS Cachan, CNRS, UniverSud, 61 Avenue du Président Wilson, F-94230 Cachan, FRANCE Email : [email protected] http://www.cmla.ens-cachan.fr/membres/aujol.html 18 september 2008 Note: This document is a working and uncomplete version, subject to errors and changes. Readers are invited to point out mistakes by email to the author. This document is intended as course notes for second year master students. The author encourage the reader to check the references given in this manuscript. In particular, it is recommended to look at [9] which is closely related to the subject of this course. Contents 1. Inverse problems in image processing 4 1.1 Introduction.................................... 4 1.2 Examples ....................................... 4 1.3 Ill-posedproblems............................... .... 6 1.4 Anillustrativeexample. ..... 8 1.5 Modelizationandestimator . ..... 10 1.5.1 Maximum Likelihood estimator . 10 1.5.2 MAPestimator ................................ 11 1.6 Energymethodandregularization. ....... 11 2. Mathematical tools and modelization 14 2.1 MinimizinginaBanachspace . 14 2.2 Banachspaces.................................... 14 2.2.1 Preliminaries ................................. 14 2.2.2 Topologies in Banach spaces . 17 2.2.3 Convexity and lower semicontinuity . ...... 19 2.2.4 Convexanalysis................................ 23 2.3 Subgradient of a convex function . ...... 23 2.4 Legendre-Fencheltransform: . ....... 24 2.5 The space of funtions with bounded variation . ......... 26 2.5.1 Introduction.................................. 26 2.5.2 Definition ................................... 27 2.5.3 Properties................................... 28 2.5.4 Decomposability of BV (Ω): ......................... 28 2.5.5 SBV ...................................... 30 2.5.6 Setsoffiniteperimeter . 32 2.5.7 Coarea formula and applications .
    [Show full text]
  • BANANAZ Panorama BANANAZ Dokumente BANANAZ Regie: Ceri Levy
    PD_4974:PD_ 26.01.2008 17:53 Uhr Seite 222 Berlinale 2008 BANANAZ Panorama BANANAZ Dokumente BANANAZ Regie: Ceri Levy Großbritannien 2008 Dokumentarfilm mit Gorillaz Länge 92 Min. Damon Albarn Format 35 mm Jamie Hewlett Farbe Ibrahim Ferrer Dennis Hopper Stabliste De La Soul Buch, Kamera Ceri Levy D-12 Schnitt Seb Monk Shaun Ryder Mischung Robert Farr Bootie Brown Musik Gorillaz Produzenten Rachel Connors Ceri Levy Produktion Head Film Ltd. 87d Elsham Road GB-London W14 8HH [email protected] Weltvertrieb Hanway Films 24 Hanway Street GB-London W1T 1UH Tel.: +44 207 2900750 Fax: +44 207 2900751 [email protected] BANANAZ Die Gorillaz sind die Band der Stunde! Während sich viele Rock- und Pop - veteranen angesichts dramatischer Rückgänge ihrer Platten- und CD-Ver - käufe neue Absatzmärkte in den visuell orientierten Vertriebskanälen Kino, Fernsehen und DVD erst noch erschließen müssen, waren die Gorillaz von vorn herein als ein visuelles Ereignis konzipiert. Als die Band 1998 von Damon Albarn, dem Sänger der britischen Gruppe Blur, und dem Comic- Zeichner Jamie Hewlett („Tank Girl“) spontan während einer nächtlichen Unterhaltung in ihrer Londoner WG gegründet wurde, bestand sie zu - nächst nur aus vier fiktiven Comic-Gestalten: D, Murdoc, Noodle und Russel. Zwar wurden sie im Laufe der Zeit mit individuellen Biografien versehen, doch verbergen sich hinter ihnen stets wechselnde Musiker. Nach mehreren Singles, zwei Alben und zahlreichen Videoclips gibt der Film von Ceri Levy nun den Blick auf die realen Personen hinter den animierten Figuren frei. Sieben Jahre lang hat sich der Regisseur, der mit Damon Albarn seit langem befreundet ist, in dem Paralleluniversum, das sich um die Gorillaz inzwischen aufgebaut hat, für seinen Film frei bewegen können.
    [Show full text]
  • EXPLICIT PARAMETERIZATION of EULER's ELASTICA 1. Introduction
    Ninth International Conference on Geometry, Geometry, Integrability and Quantization Integrability June 8–13, 2007, Varna, Bulgaria and Ivaïlo M. Mladenov, Editor IX SOFTEX, Sofia 2008, pp 175–186 Quantization EXPLICIT PARAMETERIZATION OF EULER’S ELASTICA PETER A. DJONDJOROV, MARIANA TS. HADZHILAZOVAy, IVAÏLO M. MLADENOVy and VASSIL M. VASSILEV Institute of Mechanics, Bulgarian Academy of Sciences Acad. G. Bonchev Str., Bl. 4, 1113 Sofia, Bulgaria yInstitute of Biophysics, Bulgarian Academy of Sciences Acad. G. Bonchev Str., Bl. 21, 1113 Sofia, Bulgaria Abstract. The consideration of some non-standard parametric Lagrangian leads to a fictitious dynamical system which turns out to be equivalent to the Euler problem for finding out all possible shapes of the lamina. Integrating the respective differential equations one arrives at novel explicit parameteri- zations of the Euler’s elastica curves. The geometry of the inflexional elastica and especially that of the figure “eight” shape is studied in some detail and the close relationship between the elastica problem and mathematical pendulum is outlined. 1. Introduction The elastic behaviour of roads and beams which attracts a continuous attention since the time of Galileo, Bernoulli and Euler has generated recently a renewed interest in plane [2, 3, 15], space [18] and space forms [1, 11]. The first elastic problem was posed by Galileo around 1638 who asked the question about the force required to break a beam set into a wall. James (or Jakob) Bernoulli raised in 1687 the question concerning the shape of the beam and had also succeeded in solving the case of the so called rectangular elastica (second case from the top in Fig.
    [Show full text]
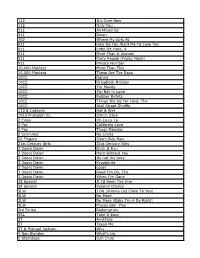
  • 112 It's Over Now 112 Only You 311 All Mixed up 311 Down
    112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question
    [Show full text]
  • Arxiv:Math/9808099V3
    On the Moduli of a Quantized Elastica in P and KdV Flows: Study of Hyperelliptic Curves as an Extension of Euler’s Perspective of Elastica I Shigeki MATSUTANI∗ and Yoshihiro ONISHIˆ † ∗8-21-1 Higashi-Linkan Sagamihara, 228-0811 Japan †Faculty of Humanities and Social Sciences, Iwate University, Ueda, Morioka, Iwate, 020-8550 Japan Abstract Quantization needs evaluation of all of states of a quantized object rather than its stationary states P with respect to its energy. In this paper, we have investigated moduli elas of a quantized elastica, a quantized loop with an energy functional associated with the Schwarz derivative,M on a Riemann sphere P. Then it is proved that its moduli space is decomposed to a set of equivalent classes determined by flows obeying the Korteweg-de Vries (KdV) hierarchy which conserve the energy. Since the flow P obeying the KdV hierarchy has a natural topology, it induces topology in the moduli space elas. P M Using the topology, is classified. Melas Studies on a loop space in the category of topological spaces Top are well-established and its cohomological properties are well-known. As the moduli space of a quantized elastica can be regarded as a loop space in the category of differential geometry DGeom, we also proved an existence of a functor between a triangle category related to a loop space in Top and that in DGeom using the induced topology. As Euler investigated the elliptic integrals and its moduli by observing a shape of classical elastica on C, this paper devotes relations between hyperelliptic curves and a quantized elastica on P as an extension of Euler’s perspective of elastica.
    [Show full text]
  • Indie Mixtape Subscribers Can Get 10% Off This Can't-Miss Set by Entering the Code JONI10 Checkout
    :: View email as a web page :: The spring of 1995 was a crowded season in indie-rock history. Pavement dropped their polarizing third album, the willfully messy and frequently brilliant Wowee Zowee. Yo La Tengo continued their hit streak of low-key masterworks with Eletr-O-Pura. Illinois fuzz-rock quartet Hum hit hard with Youʼd Prefer An Astronaut, and Teenage Fanclub produced one of their finest jangle-pop efforts, Grand Prix. Wilco, Elastica, and Apples In Stereo put out well-regarded debuts. And Red House Painters hit a new high-water mark with Ocean Beach. But even in an era when classic indie records seemed to come out every week, there was nothing quite like Alien Lanes, the eighth full-length LP by a band from Dayton, Ohio called Guided By Voices. Released on April 4, 1995, Alien Lanes arrived with baked-in mythology. It had been supposedly recorded for just $10 in various concrete basements around Dayton by a group of blue-collar guys in their mid-30s. Uproxx dug into the history of this classic and produced this great oral history. -- Steven Hyden, Uproxx Cultural Critic and author of This Isn't Happening: Radiohead's "Kid A" And The Beginning Of The 21st Century OPENING TRACKS RINA SAWAYAMA This budding indie-pop star is among the buzziest acts to emerge this year, with an ear-catching single called “STFU” that’s like Carly Rae Jepsen if she spent years obsessing over Korn’s Follow The Leader. That pan-genre approach ultimately informs Sawayama — who was born in Japan and raised in London — and her aesthetic.
    [Show full text]