Persistence Theory: from Quiver Representations to Data Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Eigenvalues of Euclidean Distance Matrices and Rs-Majorization on R2
Archive of SID 46th Annual Iranian Mathematics Conference 25-28 August 2015 Yazd University 2 Talk Eigenvalues of Euclidean distance matrices and rs-majorization on R pp.: 1{4 Eigenvalues of Euclidean Distance Matrices and rs-majorization on R2 Asma Ilkhanizadeh Manesh∗ Department of Pure Mathematics, Vali-e-Asr University of Rafsanjan Alemeh Sheikh Hoseini Department of Pure Mathematics, Shahid Bahonar University of Kerman Abstract Let D1 and D2 be two Euclidean distance matrices (EDMs) with correspond- ing positive semidefinite matrices B1 and B2 respectively. Suppose that λ(A) = ((λ(A)) )n is the vector of eigenvalues of a matrix A such that (λ(A)) ... i i=1 1 ≥ ≥ (λ(A))n. In this paper, the relation between the eigenvalues of EDMs and those of the 2 corresponding positive semidefinite matrices respect to rs, on R will be investigated. ≺ Keywords: Euclidean distance matrices, Rs-majorization. Mathematics Subject Classification [2010]: 34B15, 76A10 1 Introduction An n n nonnegative and symmetric matrix D = (d2 ) with zero diagonal elements is × ij called a predistance matrix. A predistance matrix D is called Euclidean or a Euclidean distance matrix (EDM) if there exist a positive integer r and a set of n points p1, . , pn r 2 2 { } such that p1, . , pn R and d = pi pj (i, j = 1, . , n), where . denotes the ∈ ij k − k k k usual Euclidean norm. The smallest value of r that satisfies the above condition is called the embedding dimension. As is well known, a predistance matrix D is Euclidean if and 1 1 t only if the matrix B = − P DP with P = I ee , where I is the n n identity matrix, 2 n − n n × and e is the vector of all ones, is positive semidefinite matrix. -

Polynomial Approximation Algorithms for Belief Matrix Maintenance in Identity Management
Polynomial Approximation Algorithms for Belief Matrix Maintenance in Identity Management Hamsa Balakrishnan, Inseok Hwang, Claire J. Tomlin Dept. of Aeronautics and Astronautics, Stanford University, CA 94305 hamsa,ishwang,[email protected] Abstract— Updating probabilistic belief matrices as new might be constrained to some prespecified (but not doubly- observations arrive, in the presence of noise, is a critical part stochastic) row and column sums. This paper addresses the of many algorithms for target tracking in sensor networks. problem of updating belief matrices by scaling in the face These updates have to be carried out while preserving sum constraints, arising for example, from probabilities. This paper of uncertainty in the system and the observations. addresses the problem of updating belief matrices to satisfy For example, consider the case of the belief matrix for a sum constraints using scaling algorithms. We show that the system with three objects (labelled 1, 2 and 3). Suppose convergence behavior of the Sinkhorn scaling process, used that, at some instant, we are unsure about their identities for scaling belief matrices, can vary dramatically depending (tagged X, Y and Z) completely, and our belief matrix is on whether the prior unscaled matrix is exactly scalable or only almost scalable. We give an efficient polynomial-time algo- a 3 × 3 matrix with every element equal to 1/3. Let us rithm based on the maximum-flow algorithm that determines suppose the we receive additional information that object whether a given matrix is exactly scalable, thus determining 3 is definitely Z. Then our prior, but constraint violating the convergence properties of the Sinkhorn scaling process. -

On the Eigenvalues of Euclidean Distance Matrices
“main” — 2008/10/13 — 23:12 — page 237 — #1 Volume 27, N. 3, pp. 237–250, 2008 Copyright © 2008 SBMAC ISSN 0101-8205 www.scielo.br/cam On the eigenvalues of Euclidean distance matrices A.Y. ALFAKIH∗ Department of Mathematics and Statistics University of Windsor, Windsor, Ontario N9B 3P4, Canada E-mail: [email protected] Abstract. In this paper, the notion of equitable partitions (EP) is used to study the eigenvalues of Euclidean distance matrices (EDMs). In particular, EP is used to obtain the characteristic poly- nomials of regular EDMs and non-spherical centrally symmetric EDMs. The paper also presents methods for constructing cospectral EDMs and EDMs with exactly three distinct eigenvalues. Mathematical subject classification: 51K05, 15A18, 05C50. Key words: Euclidean distance matrices, eigenvalues, equitable partitions, characteristic poly- nomial. 1 Introduction ( ) An n ×n nonzero matrix D = di j is called a Euclidean distance matrix (EDM) 1, 2,..., n r if there exist points p p p in some Euclidean space < such that i j 2 , ,..., , di j = ||p − p || for all i j = 1 n where || || denotes the Euclidean norm. i , ,..., Let p , i ∈ N = {1 2 n}, be the set of points that generate an EDM π π ( , ,..., ) D. An m-partition of D is an ordered sequence = N1 N2 Nm of ,..., nonempty disjoint subsets of N whose union is N. The subsets N1 Nm are called the cells of the partition. The n-partition of D where each cell consists #760/08. Received: 07/IV/08. Accepted: 17/VI/08. ∗Research supported by the Natural Sciences and Engineering Research Council of Canada and MITACS. -

Smith Normal Formal of Distance Matrix of Block Graphs∗†
Ann. of Appl. Math. 32:1(2016); 20-29 SMITH NORMAL FORMAL OF DISTANCE MATRIX OF BLOCK GRAPHS∗y Jing Chen1;2,z Yaoping Hou2 (1. The Center of Discrete Math., Fuzhou University, Fujian 350003, PR China; 2. School of Math., Hunan First Normal University, Hunan 410205, PR China) Abstract A connected graph, whose blocks are all cliques (of possibly varying sizes), is called a block graph. Let D(G) be its distance matrix. In this note, we prove that the Smith normal form of D(G) is independent of the interconnection way of blocks and give an explicit expression for the Smith normal form in the case that all cliques have the same size, which generalize the results on determinants. Keywords block graph; distance matrix; Smith normal form 2000 Mathematics Subject Classification 05C50 1 Introduction Let G be a connected graph (or strong connected digraph) with vertex set f1; 2; ··· ; ng. The distance matrix D(G) is an n × n matrix in which di;j = d(i; j) denotes the distance from vertex i to vertex j: Like the adjacency matrix and Lapla- cian matrix of a graph, D(G) is also an integer matrix and there are many results on distance matrices and their applications. For distance matrices, Graham and Pollack [10] proved a remarkable result that gives a formula of the determinant of the distance matrix of a tree depend- ing only on the number n of vertices of the tree. The determinant is given by det D = (−1)n−1(n − 1)2n−2: This result has attracted much interest in algebraic graph theory. -

Office of Fiscal & Monitoring Services Bureau of County Finance And
Office of Fiscal & Monitoring Services Bureau of County Finance and Technical Assistance County Points of Contact for BCFTA Help Desk REGION 1 COUNTY SERVICE LOCATION LAST NAME FIRST NAME E‐MAIL CONTACT Champaign LAA11, LAC11, LAP11 Bacon Martha [email protected] Stewart Holly [email protected] LAC21 Bowens Joyce [email protected] Delaware Gray Adeana [email protected] LAA21, LAP21 Schonauer Jacqueline [email protected] Walters Jacqueline [email protected] Fairfield LAA23, LAC23, LAP23 Brown Carri [email protected] McCoy Amy [email protected] Fayette LAA24, LAC24, LAP24 Cave Abby [email protected] Williamson Faye [email protected] Franklin LAC25 Jittkarunrat Sirina [email protected] Okafor Emeka [email protected] Knox LAA42, LAC42, LAP42 Feltman Andrea [email protected] Myers Jacqueline [email protected] LAC45 Bryan Cynthia [email protected] Licking LAA45, LAP45 Mitchell Erica [email protected] Spangler Jamie [email protected] LAA46, LAC46 Fay Sandra [email protected] Logan Fogle Cheryl [email protected] LAP46 Nease Shoan [email protected] Pugh Kathy [email protected] Madison LAA49, LAC49, LAP49 Kaifas Steve [email protected] Vickers Donna [email protected] LAA51, LAC51 Chapman Melissa [email protected] Marion Harless Julie [email protected] LAP51 Downes Patrick [email protected] Spencer Becky [email protected] Morrow LAA59, LAC59, LAP59 Keeran -
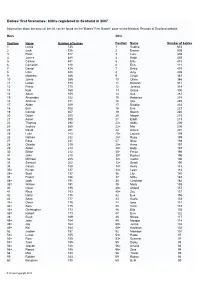
Babies' First Forenames: Births Registered in Scotland in 2007
Babies' first forenames: births registered in Scotland in 2007 Information about the basis of the list can be found via the 'Babies' First Names' page on the National Records of Scotland website. Boys Girls Position Name Number of babies Position Name Number of babies 1 Lewis 735 1 Sophie 653 2 Jack 726 2 Emma 508 3 Ryan 517 3 Lucy 438 4 James 489 4 Katie 435 5 Callum 441 5 Ellie 415 6 Cameron 428 6 Erin 414 7 Daniel 424 7 Emily 407 8 Liam 406 8 Amy 405 9 Matthew 386 9 Chloe 387 10 Jamie 385 10 Olivia 386 11 Logan 374 11 Hannah 371 12 Finlay 370 12 Jessica 318 13 Kyle 369 13 Grace 300 14 Adam 355 14 Ava 282 15 Alexander 322 15 Rebecca 274 16 Andrew 311 16 Isla 249 17 Aiden 309 17 Brooke 234 18 Ben 308 18 Eva 227 19 Connor 307 19 Niamh 220 20 Dylan 305 20 Megan 215 21 Aaron 300 21 Eilidh 213 22 Thomas 290 22= Abbie 206 23 Joshua 260 22= Mia 206 24 David 251 24 Aimee 201 25 Luke 243 25= Lauren 199 26 Nathan 232 25= Ruby 199 27 Ross 231 27 Skye 198 28 Charlie 219 28= Anna 197 29 Aidan 214 28= Holly 197 30 Ethan 212 30= Freya 196 31 John 210 30= Rachel 196 32 Michael 205 32= Caitlin 190 33 Samuel 202 32= Sarah 190 34 Calum 199 34= Keira 183 35= Kieran 197 34= Leah 183 35= Scott 197 36 Lily 180 37 Fraser 196 37 Millie 167 38= Josh 191 38 Charlotte 162 38= William 191 39 Molly 159 40 Oliver 185 40= Abigail 157 41 Rhys 183 40= Zoe 157 42 Harry 178 42 Eve 156 43 Sean 177 43 Kayla 154 44= Owen 175 44 Iona 144 44= Sam 175 45 Cara 137 46= Christopher 173 46 Ella 136 46= Robert 173 47 Evie 122 48 Euan 169 48 Nicole 117 49= Jake 164 49 Morgan 114 49= -
![Arxiv:1803.06211V1 [Math.NA] 16 Mar 2018](https://docslib.b-cdn.net/cover/2225/arxiv-1803-06211v1-math-na-16-mar-2018-382225.webp)
Arxiv:1803.06211V1 [Math.NA] 16 Mar 2018
A NUMERICAL MODEL FOR THE CONSTRUCTION OF FINITE BLASCHKE PRODUCTS WITH PREASSIGNED DISTINCT CRITICAL POINTS CHRISTER GLADER AND RAY PORN¨ Abstract. We present a numerical model for determining a finite Blaschke product of degree n + 1 having n preassigned distinct critical points z1; : : : ; zn in the complex (open) unit disk D. The Blaschke product is uniquely determined up to postcomposition with conformal automor- phisms of D. The proposed method is based on the construction of a sparse nonlinear system where the data dependency is isolated to two vectors and on a certain transformation of the critical points. The effi- ciency and accuracy of the method is illustrated in several examples. 1. Introduction A finite Blaschke product of degree n is a rational function of the form n Y z − αj (1.1) B(z) = c ; c; α 2 ; jcj = 1; jα j < 1 ; 1 − α z j C j j=1 j which thereby has all its zeros in the open unit disc D, all poles outside the closed unit disc D and constant modulus jB(z)j = 1 on the unit circle T. The overbar in (1.1) and in the sequel stands for complex conjugation. The finite Blaschke products of degree n form a subset of the rational functions of degree n which are unimodular on T. These functions are given by all fractions n ~ a0 + a1 z + ::: + an z (1.2) B(z) = n ; a0; :::; an 2 C : an + an−1 z + ::: + a0 z An irreducible rational function of form (1.2) is a finite Blaschke product when all its zeros are in D. -

Perspectives from Hazards, Disaster, and Emergency Management
CARRI Research Report 1 COMMUNITY AND REGIONAL RESILIENCE: PERSPECTIVES FROM HAZARDS, DISASTERS, AND EMERGENCY MANAGEMENT Susan L. Cutter,* Lindsey Barnes, Melissa Berry, Christopher Burton, Elijah Evans, Eric Tate, and Jennifer Webb Hazards and Vulnerability Research Institute Department of Geography University of South Carolina Columbia, South Carolina *Carolina Distinguished Professor and Director of the Hazards and Vulnerability Research Institute Date Published: September 2008 Community and Regional Resilience Initiative RESEARCH FINDINGS ABOUT COMMUNITY AND REGIONAL RESILIENCE One of the commitments of the Community and Regional Resilience Initiative (CARRI) is to understand what resilience is and how to get there, based on research evidence. As one resource for this effort, CARRI has commissioned a number of summaries of existing knowledge about resilience, arising from a number of different research traditions. This paper is one in a series of such summaries, which will be integrated with new resilience explorations in several CARRI partner cities and with further discussions with the research community and other stakeholders to serve as the knowledge base for the initiative. For further information about CARRI’s research component, contact Thomas J. Wilbanks, [email protected], or Sherry B. Wright, [email protected]. CARRI Research Report 1 iii Community and Regional Resilience Initiative COMMUNITY AND REGIONAL RESILIENCE INITIATIVE Oak Ridge National Laboratory’s (ORNL) Community and Regional Resilience Initiative (CARRI) -

Marilyn Chidlow Volunteer Award Recipients Archives
Marilyn Chidlow Volunteer Award Recipient Name Club/Skating School Year Recognized Ainsley Doren Ice Edge SC 2020 Alana Forbes Calgary Synchronized SC 2016 Alexia Wagner Figure 8 Skating Club 2018 Alison Mica Derrick Skating Club 2018 Alison Piekema Lethbridge SC 2020 Allison Edwards Grovedale SC 2013 Allison Edwards Grovedale SC 2015 Allison Reynolds Pincher Creek SC 2020 Amanda Houlihan Gibbons SC 2016 Amanda Kavanagh Rainbow Lake SC 2013 Amanda Knock Innisfail SC 2019 Amanda Zimmer Claresholm SC 2010 Andrea Chan Southern Alberta Skating Academy 2018 Angela Stark Grimshaw SC 2015 Angela Walburger Cardston SC 2015 Angeline Chura Edmonton Synchronized Skating Club 2011 Angie Wedge East Smoky SC 2013 Anita Mortensen St. Paul FSC 2013 Anjeanette Klein Barrhead FSC 2020 Anne Bateman Beaverlodge SC 2013 Anne Bridgman Glacier School of Skating 2011 Anne Marie Behnke Peace River Skating Club 2019 Anne Saliwonchuk Nampa SC 2012 Anne Saliwonchuk Nampa SC 2013 Updated: June 11, 2020 Marilyn Chidlow Volunteer Award Recipient Name Club/Skating School Year Recognized Anneli Porter Derrick SC 2016 Annette Yanishewski Grande Prairie SC 2015 April Steele Lakeside FSC 2020 Asha Sargunaraj Lakeside FSC 2016 Barb Huber Grimshaw SC 2011 Barb Nakashima Taber Figure SC 2020 Barb Rauch Rocky FSC 2008 Beata North Wild Rose FSC 2015 Becky Burgess Calgary Synchronized SC 2016 Belinda Cunningham Carstairs SC 2011 Bellinda Kelly Wainwright SC 2015 Bernadette Vankosky Edson FSC 2017 Bernadine Duquette Drayton Valley SC 2013 Bernadine Kosiorek Okotoks SC 2010 Beth Patton-Collier Cypress School of Skating 2008 Bev Gray Canmore SC 2012 Bev MacDonald Clive FSC 2009 Bev Padget Stony Plain SC 2011 Bev Yasinski Manning SC 2013 Bobbie Jo Gold Medicine Hat SC 2013 Bobbie Kelly Calgary Winter Club 2018 Bobbie-Shannon Finnebraaten Grande Prairie Skating Club 2018 Bobbi-Jo Martin Lethbridge SC 2014 Bonnie Smyl St. -

Berrien County Departments
COUNTY DEPARTMENTS Conference Call Phone ............................................ 8856 911 ADMINISTRATION / COUNTY Conference Room 4B .............................................. 8298 PUBLIC–SAFETY DISPATCH Kenneth Wendzel Conference Room ...................... 8259 Empire – 2100 E. Empire, Benton Harbor, MI 49022 Otto Grau Conference Room ................................... 8204 BLURTON, Sara Jane – QA Supervisor……………4966 FLICK, Jennifer – Asst. Director……………………..4958 Commissioners SAMPSELL, Caitlin – Director ................................. 4967 Admin Center – 701 Main St., St. Joseph, MI 49085 SMITH, Tami – 911 Data Center............................. 4979 BELL, Rayonte ...................................... District 5 – 8095 CURRAN, Jim ..................................... District 11 – 8095 Dispatch Center ELLIOTT, McKinley R. ........................ District 10 – 8095 FREEHLING, Teri Sue .......................... District 8 – 8095 DISPATCH ...................... 4900, 4901, 4902, 4909, 4910 HARRISON, Robert P…………………...District 7 – 8095 HINKELMAN, Jon ................................. District 2 – 8095 LEIN – Police Dispatch ................................. 4903, 4908 MAJEREK, Michael J. ........................ District 12 – 8095 MEEKS, Don ......................................... District 3 – 8095 BALLARD, Steven…………………………………….4900 SCOTT, Ezra A. ................................... District 9 – 8095 BENSTINE, Jeremy…………………………………..4900 VOLLRATH, David ................................ District 1 – 8095 BURKS, Kristina -

Essays on Strategic Behavior in the U.S. Airline Industry
Essays on Strategic Behavior in the U.S. Airline Industry Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Kerria Measkhan Tan, B.A., M.A. Graduate Program in Economics The Ohio State University 2012 Dissertation Committee: Matthew Lewis, Advisor James Peck Huanxing Yang c Copyright by Kerria Measkhan Tan 2012 Abstract In my first dissertation essay, \Incumbent Response to Entry by Low-Cost Carri- ers in the U.S. Airline Industry," I analyze the price response of incumbents to entry by low-cost carriers in the U.S. airline industry. Previous theoretical papers suggest that airlines might respond to entry by lowering prices to compete harder for existing customers or they might increase prices to exploit their brand-loyal customers. This paper tests which effect is more prominent in the airline industry. I find that when one of four low-cost carriers enters a particular route, legacy carrier incumbents respond differently than low-cost carrier incumbents to new low-cost carrier entry. Legacy carriers decrease their mean airfare, 10th percentile airfare, and 90th percentile air- fare before and after entry by a low-cost carrier. However, low-cost carriers do not significantly alter their pricing strategy. The differing incumbent responses can be attributed to the finding that low-cost carrier entrants tend to match the price set by rival low-cost carriers in the quarter of entry and tend to enter with a lower price than that of legacy carrier incumbents. The results also suggest that entry does not affect price dispersion by incumbent carriers. -

FIRST NAME MI LAST NAME FELLOW DATE SECTION Theodore A
FIRST NAME MI LAST NAME FELLOW DATE SECTION Theodore A. Aanstoos 04/01/2001 Cent Texas Said I. Abdel-Khalik 06/01/1999 Atlanta Rohan C. Abeyaratne 03/01/1998 Boston H. Norman Abramson 01/01/1971 San Antonio Memis Acar 06/01/2007 United Kingd Salvador M. Aceves-Saborio 07/01/2001 Sumanta Acharya 08/05/2008 Baton Rouge Jan D. Achenbach 01/01/1979 Chicago Allan J. Acosta 01/01/1979 Orange Cnty Paul J. Adam 10/01/1997 Arizona John J. Adamczyk 02/01/2001 Cleveland Frank C. Adamek 05/01/1997 Nw Houston Douglas E. Adams 03/18/2011 Cent Indiana George G. Adams 05/01/1995 Boston John C. Adams 07/01/1995 Highland Rim William J. Adams 11/01/2000 Santa Clara Alva L. Addy 01/01/1984 Nebraska Kenneth L. Adler 01/01/1986 San Fernando Suresh G. Advani 06/01/1999 Delaware Abdollah Afjeh 04/02/2012 Nw Ohio Naval K. Agarwal 05/01/1996 Western Wash Ramesh K. Agarwal 02/01/1994 St Louis Avinash K. Agarwal 9/1/2013 India Mahesh Aggarwal 10/01/1995 Erie Suresh K. Aggarwal 06/01/2005 Chicago Alice M. Agogino 10/01/2005 San Francisc Ajay K. Agrawal 09/01/2004 Birmingham Giridhari L. Agrawal 04/01/2004 Hartford Sunil K. Agrawal 01/01/2004 Delaware John W. Ahlen 05/01/2003 Arkansas Arthur G. Ahlstone 12/01/1988 Channel Isl Goodarz Ahmadi 03/01/1997 Syracuse Mehdi Ahmadian 05/01/1998 Virginia A. K. W. Ahmed 10/02/2012 Quebec Xiaolan Ai 04/02/2012 Canton-All-M Adnan Akay 09/01/1989 Pittsburgh Hadi K.