Optical Properties of Materials JJL Morton
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 4 Reflected Light Optics
l CHAPTER 4 REFLECTED LIGHT OPTICS 4.1 INTRODUCTION Light is a form ofelectromagnetic radiation. which may be emitted by matter that is in a suitably "energized" (excited) state (e.g.,the tungsten filament ofa microscope lamp emits light when "energized" by the passage of an electric current). One ofthe interesting consequences ofthe developments in physics in the early part of the twentieth century was the realization that light and other forms of electromagnetic radiation can be described both as waves and as a stream ofparticles (photons). These are not conflicting theories but rather complementary ways of describing light; in different circumstances. either one may be the more appropriate. For most aspects ofmicroscope optics. the "classical" approach ofdescribing light as waves is more applicable. However, particularly (as outlined in Chapter 5) when the relationship between the reflecting process and the structure and composition ofa solid is considered. it is useful to regard light as photons. The electromagnetic radiation detected by the human eye is actually only a very small part of the complete electromagnetic spectrum, which can be re garded as a continuum from the very low energies and long wavelengths characteristic ofradio waves to the very high energies (and shortwavelengths) of gamma rays and cosmic rays. As shown in Figure 4.1, the more familiar regions ofthe infrared, visible light, ultraviolet. and X-rays fall between these extremes of energy and wavelength. Points in the electromagnetic spectrum can be specified using a variety ofenergy or wavelength units. The most com mon energy unit employed by physicists is the electron volt' (eV). -

Optical Properties of Tio2 Based Multilayer Thin Films: Application to Optical Filters
Int. J. Thin Fil. Sci. Tec. 4, No. 1, 17-21 (2015) 17 International Journal of Thin Films Science and Technology http://dx.doi.org/10.12785/ijtfst/040104 Optical Properties of TiO2 Based Multilayer Thin Films: Application to Optical Filters. M. Kitui1, M. M Mwamburi2, F. Gaitho1, C. M. Maghanga3,*. 1Department of Physics, Masinde Muliro University of Science and Technology, P.O. Box 190, 50100, Kakamega, Kenya. 2Department of Physics, University of Eldoret, P.O. Box 1125 Eldoret, Kenya. 3Department of computer and Mathematics, Kabarak University, P.O. Private Bag Kabarak, Kenya. Received: 6 Jul. 2014, Revised: 13 Oct. 2014, Accepted: 19 Oct. 2014. Published online: 1 Jan. 2015. Abstract: Optical filters have received much attention currently due to the increasing demand in various applications. Spectral filters block specific wavelengths or ranges of wavelengths and transmit the rest of the spectrum. This paper reports on the simulated TiO2 – SiO2 optical filters. The design utilizes a high refractive index TiO2 thin films which were fabricated using spray Pyrolysis technique and low refractive index SiO2 obtained theoretically. The refractive index and extinction coefficient of the fabricated TiO2 thin films were extracted by simulation based on the best fit. This data was then used to design a five alternating layer stack which resulted into band pass with notch filters. The number of band passes and notches increase with the increase of individual layer thickness in the stack. Keywords: Multilayer, Optical filter, TiO2 and SiO2, modeling. 1. Introduction successive boundaries of different layers of the stack. The interface formed between the alternating layers has a great influence on the performance of the multilayer devices [4]. -

Investigation of Dichroism by Spectrophotometric Methods
Application Note Glass, Ceramics and Optics Investigation of Dichroism by Spectrophotometric Methods Authors Introduction N.S. Kozlova, E.V. Zabelina, Pleochroism (from ancient greek πλέον «more» + χρόμα «color») is an optical I.S. Didenko, A.P. Kozlova, phenomenon when a transparent crystal will have different colors if it is viewed from Zh.A. Goreeva, T different angles (1). Sometimes the color change is limited to shade changes such NUST “MISiS”, Russia as from pale pink to dark pink (2). Crystals are divided into optically isotropic (cubic crystal system), optically anisotropic uniaxial (hexagonal, trigonal, tetragonal crystal systems) and optically anisotropic biaxial (orthorhombic, monoclinic, triclinic crystal systems). The greatest change is limited to three colors. It may be observed in biaxial crystals and is called trichroic. A two color change may be observed in uniaxial crystals and called dichroic. Pleochroic is often the term used to cover both (2). Pleochroism is caused by optical anisotropy of the crystals Dichroism can be observed in non-polarized light but in (1-3). The absorption of light in the optically anisotropic polarized light it may be more pronounced if the plane of crystals depends on the frequency of the light wave and its polarization of incident light matches plane of polarization of polarization (direction of the electric vector in it) (3, 4). light that propagates in the crystal—ordinary or extraordinary Generally, any ray of light in the optical anisotropic crystal is wave. divided into two rays with perpendicular polarizations and The difference in absorbance of ray lights may be minor, but different velocities (v1, v2) which are inversely proportional to it may be significant and should be considered both when the refractive indices (n1, n2) (4). -
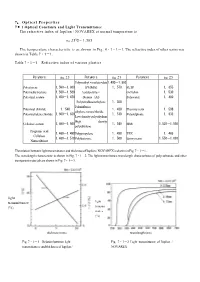
7.1 Optical Constants and Light Transmittance
7 . Optical Properties 7・ 1 Optical Constants and Light Transmittance The refractive index of Iupilon / NOVAREX at normal temperature is nD 25℃ = 1,585 The temperature characteristic is as shown in Fig. 4・1・1‐1. The refractive index of other resins was shown in Table 7・1‐1. Table 7・1‐1 Refractive index of various plastics Polymers nD 25 Polymers nD 25 Polymers nD 25 Polymethyl・methacrylate1.490‐1.500 Polystyrene 1.590‐1.600 (PMMA) 1.570 PETP 1.655 Polymethylstyrene 1.560‐1.580 Acrylonitrile・ 66 Nylon 1.530 Polyvinyl acetate 1.450‐1.470 Styrene(AS Polyacetal 1.480 Polytetrafluoroethylene 1.350 Polutrifluoro Polyvinyl chloride 1.540 1.430 Phenoxy resin 1.598 ethylene monochloride Polyvinylidene chloride 1.600‐1.630 1.510 Polysulphone 1.633 Low density polyethylene High density Cellulose acetate 1.490‐1.500 1.540 SBR 1.520‐1.550 polyethylene Propionic acid 1.460‐1.490 Polypropylene 1.490 TPX 1.465 Cellulose 1.460‐1.510 Polybutyrene 1.500 Epoxy resin 1.550‐1.610 Nitrocellulose The relation between light transmittance and thickness of Iupilon / NOVAREX is shown in Fig. 7・1‐1. The wavelength characteristic is shown in Fig. 7・1‐2. The light transmittance wavelength characteristics of polycarbonate and other transparent materials are shown in Fig. 7・1‐3. light transmittance light (%) transmi- ttance (%) thickness (mm) wavelength (nm) Fig. 7・1‐1 Relation between light Fig. 7・1‐2 Light transmittance of Iupilon / transmittancee and thickness of Iupilon / NOVAREX NOVAREX glass 5.72mm injection molding PMMA 3.43mm compression molding light 3.25mm transmittance injection molding (%) PC 3.43mm wavelength (nm) Fig. -

Radiometry of Light Emitting Diodes Table of Contents
TECHNICAL GUIDE THE RADIOMETRY OF LIGHT EMITTING DIODES TABLE OF CONTENTS 1.0 Introduction . .1 2.0 What is an LED? . .1 2.1 Device Physics and Package Design . .1 2.2 Electrical Properties . .3 2.2.1 Operation at Constant Current . .3 2.2.2 Modulated or Multiplexed Operation . .3 2.2.3 Single-Shot Operation . .3 3.0 Optical Characteristics of LEDs . .3 3.1 Spectral Properties of Light Emitting Diodes . .3 3.2 Comparison of Photometers and Spectroradiometers . .5 3.3 Color and Dominant Wavelength . .6 3.4 Influence of Temperature on Radiation . .6 4.0 Radiometric and Photopic Measurements . .7 4.1 Luminous and Radiant Intensity . .7 4.2 CIE 127 . .9 4.3 Spatial Distribution Characteristics . .10 4.4 Luminous Flux and Radiant Flux . .11 5.0 Terminology . .12 5.1 Radiometric Quantities . .12 5.2 Photometric Quantities . .12 6.0 References . .13 1.0 INTRODUCTION Almost everyone is familiar with light-emitting diodes (LEDs) from their use as indicator lights and numeric displays on consumer electronic devices. The low output and lack of color options of LEDs limited the technology to these uses for some time. New LED materials and improved production processes have produced bright LEDs in colors throughout the visible spectrum, including white light. With efficacies greater than incandescent (and approaching that of fluorescent lamps) along with their durability, small size, and light weight, LEDs are finding their way into many new applications within the lighting community. These new applications have placed increasingly stringent demands on the optical characterization of LEDs, which serves as the fundamental baseline for product quality and product design. -

Schott Filter Catalog
Definitions Glass Filters 2009 OPTICAL FILTERS TABLE OF CONTENTS Table of Contents Foreword ....................................................................................... 4 1. General information on the catalog data ..................................... 5 2. SCHOTT glass filter catalog: product line ..................................... 6 3. Applications for SCHOTT glass filters ............................................ 7 4. Material: filter glass ..................................................................... 10 4.1 Group names ................................................................................ 10 4.2 Classification ................................................................................. 10 4.2.1 Base glasses .................................................................................. 10 4.2.2 Ionically colored glasses ................................................................. 10 4.2.3 Colloidally colored glasses ............................................................. 11 4.3 Reproducibility of transmission ...................................................... 11 4.4 Thermal toughening ..................................................................... 11 5. Filter glass properties .................................................................. 13 5.1 Mechanical density ........................................................................ 13 5.2 Transformation temperature .......................................................... 13 5.3 Thermal expansion ....................................................................... -

Method of Determining the Optical Properties of Ceramics and Ceramic Pigments: Measurement of the Refractive Index
CASTELLÓN (SPAIN) METHOD OF DETERMINING THE OPTICAL PROPERTIES OF CERAMICS AND CERAMIC PIGMENTS: MEASUREMENT OF THE REFRACTIVE INDEX A. Tolosa(1), N. Alcón(1), F. Sanmiguel(2), O. Ruiz(2). (1) AIDO, Instituto tecnológico de Óptica, Color e Imagen, Spain. (2) Torrecid, S.A., Spain. ABSTRACT The knowledge of the optical properties of materials, such as pigments or the ceramics that contain these, is a key feature in modelling the behaviour of light when it impinges upon them. This paper presents a method of obtaining the refractive index of ceramics from diffuse reflectance measurements made with a spectrophotometer equipped with an integrating sphere. The method has been demonstrated to be applicable to opaque ceramics, independently of whether the surface is polished or not, thus avoiding the need to use different methods to measure the refractive index accor- ding to the surface characteristics of the material. This method allows the Fresnel equations to be directly used to calculate the refractive index with the measured diffuse reflectance, without needing to measure just the specular reflectance. Al- ternatively, the method could also be used to measure the refractive index in transparent and translucent samples. The technique can be adapted to determine the complex refractive index of pigments. The reflectance measurement would be based on the method proposed in this paper, but for the calculation of the real part of the refractive index, related to the change in velocity that light undergoes when it reaches the material, and the imaginary part, related to light absorption by the material, the Kramers-Kronig relations would be used. -

SOLID STATE PHYSICS PART II Optical Properties of Solids
SOLID STATE PHYSICS PART II Optical Properties of Solids M. S. Dresselhaus 1 Contents 1 Review of Fundamental Relations for Optical Phenomena 1 1.1 Introductory Remarks on Optical Probes . 1 1.2 The Complex dielectric function and the complex optical conductivity . 2 1.3 Relation of Complex Dielectric Function to Observables . 4 1.4 Units for Frequency Measurements . 7 2 Drude Theory{Free Carrier Contribution to the Optical Properties 8 2.1 The Free Carrier Contribution . 8 2.2 Low Frequency Response: !¿ 1 . 10 ¿ 2.3 High Frequency Response; !¿ 1 . 11 À 2.4 The Plasma Frequency . 11 3 Interband Transitions 15 3.1 The Interband Transition Process . 15 3.1.1 Insulators . 19 3.1.2 Semiconductors . 19 3.1.3 Metals . 19 3.2 Form of the Hamiltonian in an Electromagnetic Field . 20 3.3 Relation between Momentum Matrix Elements and the E®ective Mass . 21 3.4 Spin-Orbit Interaction in Solids . 23 4 The Joint Density of States and Critical Points 27 4.1 The Joint Density of States . 27 4.2 Critical Points . 30 5 Absorption of Light in Solids 36 5.1 The Absorption Coe±cient . 36 5.2 Free Carrier Absorption in Semiconductors . 37 5.3 Free Carrier Absorption in Metals . 38 5.4 Direct Interband Transitions . 41 5.4.1 Temperature Dependence of Eg . 46 5.4.2 Dependence of Absorption Edge on Fermi Energy . 46 5.4.3 Dependence of Absorption Edge on Applied Electric Field . 47 5.5 Conservation of Crystal Momentum in Direct Optical Transitions . 47 5.6 Indirect Interband Transitions . -

Optical Properties of Polymeric Materials for Concentrator Photovoltaic Systems
Solar Energy Materials & Solar Cells 95 (2011) 2077–2086 Contents lists available at ScienceDirect Solar Energy Materials & Solar Cells journal homepage: www.elsevier.com/locate/solmat Optical properties of polymeric materials for concentrator photovoltaic systems R.H. French a,b,n, J.M. Rodrı´guez-Parada a, M.K. Yang a, R.A. Derryberry a, N.T. Pfeiffenberger a a DuPont Company, Central Research, Exp. Sta., Wilmington, DE 19880, USA b Department of Materials Science & Engineering, 510 White Hall, 2111 Martin Luther King Jr. Drive, Case Western Reserve University, Cleveland, OH 44106-7204, USA article info abstract Article history: As part of our research on materials for concentrator photovoltaics (CPV), we are evaluating the Received 30 July 2010 optical properties and solar radiation durability of a number of polymeric materials with potential Accepted 23 February 2011 in CPV applications. For optical materials in imaging or non-imaging optical systems, detailed Available online 8 May 2011 knowledge of the wavelength-dependent complex index of refraction is important for system Keywords: design and performance, yet optical properties for many polymeric systems are not available in the Fluoropolymer literature. Here we report the index of refraction, optical absorbance, haze, and Urbach edge Ethylene backbone polymer analysis results of various polymers of interest for CPV systems. These values were derived from Polyimide ellipsometry and from using a VUV-VASE and transmission based absorbance spectroscopy on thick Index of refraction film samples. Optical absorbance Fluoropolymers such as poly(tetrafluoroethylene-co-hexafluoropropylene) (Teflons FEP), poly(te- Haze trafluoroethylene-co-perfluoropropyl vinyl ether) (Teflons PFA) and poly(ethylene-co-tetrafluoroethy- lene) (Teflons ETFE Film) have desirable optical and physical properties for optical applications in CPV. -

Optical Properties of Paper: Theory and Practice
Preferred citation: R. Farnood. Review: Optical properties of paper: theory and practice. In Advances in Pulp and Paper Research, Oxford 2009, Trans. of the XIVth Fund. Res. Symp. Oxford, 2009, (S.J. I’Anson, ed.), pp 273–352, FRC, Manchester, 2018. DOI: 10.15376/frc.2009.1.273. OPTICAL PROPERTIES OF PAPER: THEORY AND PRACTICE Ramin Farnood Department of Chemical Engineering and Applied Chemistry University of Toronto, February 25, 2009, Revised: May 22, 2009 ABSTRACT The perceived value of paper products depends not only upon their performance but also upon their visual appeal. The optical properties of paper, including whiteness, brightness, opacity, and gloss, affect its visual perception and appeal. From a practical point of view, it is important to quantify these optical properties by means of reliable and repeatable measurement methods, and furthermore, to relate these measured values to the structure of paper and characteristics of its constituents. This would allow papermakers to design new products with improved quality and reduced cost. In recent years, significant progress has been made in terms of the fundamental understanding of light-paper inter- action and its effect on paper’s appearance. The introduction of digital imaging technology has led to the emergence of a new category of optical testing methods and has provided fresh insights into the relationship between paper’s structure and its optical properties. These developments were complemented by advances in the theoretical treatment of light propagation in paper. In particular, wave scattering theories in random media are finding increasing applicability in gaining a better understanding of the optical properties of paper. -

Optical Properties, Definitions and Measurements
LIGHTING APPLICATION GUIDE Application center Glossary Optical properties, definitions and measurements to optical testing terminology, with a description of how optical As the power and utility of LEDs has grown, so has the use of properties are measured and calculated by Dow, as well as the optical-grade silicones. Their versatility and unique physical definitions used in its specifications. properties allow silicones to now be used in many new ways Optical properties such as light pipes, lenses and other secondary optics. The three principle effects on light interacting with matter are Optical properties are critical to material and design choice, Reflection (R), Absorption (A) and Transmission (T). impacting device performance. Unfortunately, not everyone defines the measurements identically. This bulletin is a guide Rdif Tdif T Lo Direct Transmission A Direct reflection Sample (medium) Definitions Absorption: Light that is “captured” by and dissipated as heat within a material as it passes through. Absorption, calculated (Ac): The measured absorption of a material mathematically corrected for a single pass through a sample correcting for the effect of reflections. Absorption coefficientα ( ): The material specific exponential coefficient defining transmission or absorption for a given sample thickness. This quantity is independent of sample thickness, thus two thicknesses of the same material will give the same absorption coefficient α, though different values of absorption A. Absorption, measured (A): The amount of light absorbed as measured as the difference between the source power and the transmitted and reflected light, including any effects of multiple reflection. Calculated reflection Albedo: Proportion of light scattered upon surface reflection Light reflects off all surfaces of a material and in many (See Reflection, diffuse) to the incident light. -

The Optical Properties of Aerosols at the Summit of Mount Tai in May and June and the Retrieval of the Complex Refractive Index
atmosphere Article The Optical Properties of Aerosols at the Summit of Mount Tai in May and June and the Retrieval of the Complex Refractive Index Dapeng Zhao 1,2 , Yan Yin 1,2,*, Min Zhang 3,4, Honglei Wang 1,2, Chunsong Lu 1,2, Liang Yuan 5 and Shuangshuang Shi 1,2 1 Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science & Technology, Nanjing 210044, China; [email protected] (D.Z.); [email protected] (H.W.); [email protected] (C.L.); [email protected] (S.S.) 2 Key Laboratory for Aerosol-Cloud-Precipitation of China Meteorological Administration, School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China 3 Tianjin Environmental Meteorological Center, Tianjin 300074, China; [email protected] 4 Tianjin Institute of Meteorology, Tianjin 300074, China 5 Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, School of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225, China; [email protected] * Correspondence: [email protected] Received: 14 May 2020; Accepted: 16 June 2020; Published: 19 June 2020 Abstract: To study the optical properties of background atmospheric aerosols in East China, we carried out observations of the physical, chemical and optical properties of atmospheric aerosols at the summit of Mount Tai (Mt. Tai, 1533.7 m above sea level) from 13 May to 25 June 2017. The results show that the average scattering coefficient (σsca,550) at 550 nm of the aerosols at the summit of Mt. Tai 1 1 is 40.3 Mm− , and the average absorption coefficient (σabs,550) at 550 nm is 16.0 Mm− .