DOCSLIB.ORG

Activation of Leinamycin by Thiols: a Theoretical Study

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Activation of Leinamycin by Thiols: a Theoretical Study Activation of Leinamycin by Thiols: A Theoretical Study Leonid Breydo and Kent S. Gates* Departments of Chemistry and Biochemistry, University of Missouri-Columbia, Columbia, Missouri 65211 [email protected] Received August 27, 2002 Reaction of thiols with the 1,2-dithiolan-3-one 1-oxide heterocycle found in leinamycin (1) results in the conversion of this antitumor antibiotic to a DNA-alkylating episulfonium ion (5). While the products formed in this reaction have been rationalized by a mechanism involving initial attack of thiol on the central sulfenyl sulfur (S2′) of the 1,2-dithiolan-3-one 1-oxide ring, the carbonyl carbon (C3′) and the sulfinyl sulfur (S1′) of this heterocycle are also expected to be electrophilic. Therefore, it is important to consider whether nucleophilic attack of thiol at these sites might contribute either to destruction of the antibiotic or conversion to its episulfonium ion form. To address this question, we have used computational methods to examine the attack of methyl thiolate on each of the three electrophilic centers in a simple analogue of the 1,2-dithiolan-3-one 1-oxide heterocycle found in leinamycin. Calculations were performed at the MP2/6-311+G(3df,p)//B3LYP/6-31G* level of theory with inclusion of solvent effects. The results indicate that the most reasonable mechanism for thiol- mediated activation of leinamycin involves initial attack of thiolate at the S2′-position of the antibiotic’s 1,2-dithiolan-3-one 1-oxide heterocycle, followed by conversion to the 1,2-oxathiolan- 5-one intermediate (3). Introduction of oxygen radicals,11,12 while the 1,2-oxathiolan-5-one form of leinamycin (3) undergoes a unique rearrangement Structurally novel natural products that possess potent to produce a DNA-alkylating episulfonium ion (5).13 The biological activity are of significant interest because their studies described here embrace the previous assump- - mechanisms of action are often unique and unexpected.1 3 tion10,13,14 that the oxathiolanone 3 represents an “acti- For this reason, we have been inspired to study the DNA- vated” form of leinamycin that serves as the immediate - damaging natural product leinamycin.4 7 This natural precursor to the episulfonium ion (5). This notion is product possesses a unique chemical structure, displays supported by a wealth of precedents showing that sulfe- potent anticancer activity, and reacts with DNA by a nyl carboxylates react readily with alkenes to yield completely novel sequence of reactions. DNA damage by episulfonium ions (Scheme 2).15 leinamycin is triggered by attack of thiols on the 1,2- The products formed in the reaction of leinamycin with dithiolan-3-one 1-oxide heterocycle of the antibiotic thiols have been rationalized by a mechanism involving - (Scheme 1).7 9 This reaction produces two crucial reactive initial attack of thiols on the central, sulfenyl sulfur (S2′) intermediates: an 1,2-oxathiolan-5-one (3) and a hydro- of the 1,2-dithiolan-3-one 1-oxide heterocycle as shown disulfide (or persulfide) 4.10 The hydrodisulfide interme- in Scheme 1.10,13 However, the carbonyl carbon (C3′) and diate (4) mediates oxidative DNA damage via production the sulfinyl sulfur (S1′) are also expected to be electro- philic. Thus, it is important to consider whether nucleo- * Address correspondence to this author. Phone: (573) 882-6763. philic attack of thiol at these sites might contribute to Fax: (573) 882-2754. either the activation or destruction of leinamycin. To (1) Gates, K. S. In Comprehensive Natural Products Chemistry; Kool, E. T., Ed.; Pergamon: New York, 1999; Vol. 7, pp 491-552. (2) Verdine, G. L. Nature 1996, 384 (supplement), 11-13. (11) Behroozi, S. J.; Kim, W.; Dannaldson, J.; Gates, K. S. Biochem- (3) Newman, D. J.; Cragg, G. M.; Snader, K. M. Nat. Prod. Rep. istry 1996, 35, 1768-1774. 2000, 17, 215-234. (12) Mitra, K.; Kim, W.; Daniels, J. S.; Gates, K. S. J. Am. Chem. (4) Hara, M.; Takahashi, I.; Yoshida, M.; Kawamoto, I.; Morimoto, Soc. 1997, 119, 11691-11692. M.; Nakano, H. J. Antibiot. 1989, 42, 333-335. (13) Asai, A.; Hara, M.; Kakita, S.; Kanda, Y.; Yoshida, M.; Saito, (5) Hara, M.; Asano, K.; Kawamoto, I.; Takiguchi, T.; Katsumata, H.; Saitoh, Y. J. Am. Chem. Soc. 1996, 118, 6802-6803. S.; Takahashi, K.; Nakano, H. J. Antibiot. 1989, 42, 1768-1774. (14) Breydo, L.; Zang, H.; Mitra, K.; Gates, K. S. J. Am. Chem. Soc. (6) Hara, M.; Saitoh, Y.; Nakano, H. Biochemistry 1990, 29, 5676- 2001, 123, 2060-2061. 5681. (15) (a) Havlik, A. J.; Kharasch, N. J. Am. Chem. Soc. 1956, 78, (7) Gates, K. S. Chem. Res. Toxicol. 2000, 13, 953-956. 1207-1210. (b) Putnam, R. E.; Sharkey, W. H. J. Am. Chem. Soc. 1957, (8) Hara, M.; Yoshida, M.; Nakano, H. Biochemistry 1990, 29, 79, 6526-6529. (c) Brydon, A.; Cameron, G. G.; Hogg, D. R. Int. J. 10449-10455. Sulfur Chem. A 1972, 2, 289-290. (d) Morishita, T.; Furukawa, N.; (9) For activation of leinamycin by other nucleophiles, see: Zang, Oae, S. Tetrahedron 1981, 37, 2539-2546. (e) Schank, K.; Frisch, A.; H.; Breydo, L.; Mitra, K.; Dannaldson, J.; Gates, K. S. Bioorg. Med. Zwanenburg, B. J. Org. Chem. 1983, 48, 4580-4582. (f) Morin, R. B.; Chem. Lett. 2001, 11, 1511-1515. Jackson, B. G.; Mueller, R. A.; Lavagnino, E. R.; Scanlon, W. B.; (10) Behroozi, S. B.; Kim, W.; Gates, K. S. J. Org. Chem. 1995, 60, Andrews, S. L. J. Am. Chem. Soc. 1963, 85, 1896-1897. (g) Vedejs, 3964-3966. E.; Mullins, M. J. J. Org. Chem. 1979, 44, 2947-48. 10.1021/jo020568l CCC: $22.00 © 2002 American Chemical Society 9054 J. Org. Chem. 2002, 67, 9054-9060 Published on Web 11/13/2002 Activation of Leinamycin by Thiols SCHEME 1 SCHEME 2 but nonetheless provides a reasonable estimate of the molecular geometry in solution. The solvent dielectric constant for dichloromethane ( ) 8.93) was used because this solvent has been used in some of the experimental work on this system.10 Frequency calculations were performed at all station- ary points at the B3LYP/6-31G* level using an Onsager address this question, we have used computational model, and a correct number of imaginary frequencies methods to examine the attack of methyl thiolate on each were found. Zero-point vibrational and thermal correc- of the three electrophilic centers in a simple analogue of tions were calculated at the same level and were not the 1,2-dithiolan-3-one 1-oxide heterocycle found in leina- scaled.21 All transition states were analyzed either by mycin. calculating an intrinsic reaction coordinate (IRC) or by visual inspection of the transition vector with the pro- gram Vibrate.22 Since entropy plays an important role Computational Methods in bimolecular reactions described here, all energies are All calculations were carried out utilizing Gaussian 94 reported as Gibbs free energy (∆G) values at 298 K. or Gaussian 98.16 All geometries were optimized and Solvation energies were calculated on the optimized frequencies calculated at the B3LYP/6-31G* level of geometries utilizing three SCRF models: integral equa- theory17,18 in the solvent model using the self-consistent tion formalism polarized continuum model (IEFPCM),23 reaction field (SCRF) method based on the Onsager polarized continuum model (PCM),24-26 and isodensity model.19,20 Reoptimization of several representative struc- polarized continuum model (IPCM)25 at the B3LYP/6- tures at higher levels (B3LYP/6-31+G* or MP2/6-31G*) 31G* level. In the models used, solvent is assumed to be did not lead to significant changes in geometry. The a continuous medium with a dielectric constant that representation of solvent used here is somewhat crude surrounds a cavity containing the solute and the shape of the cavity is adjusted to fit the shape of the solute (16) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, M. A.; molecule to afford more accurate solvation energies. All Gill, P. M. W.; Johnson, B. G.; Robb, M. A.; Cheeseman, J. R.; Keith, three models show qualitatively similar results, and PCM T. A. P.; Petersson, G. A.; Montgomery, J. A.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, and IEFPCM afford nearly identical solvation energies O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennuci, B.; Pomelli, (see Tables S1 and S2 and Scheme 4). Values shown in C.; Adamo, C.; Clifford, S.; Ochterski, G.; Cui, Q.; Morokuma, K.; Scheme 4 are derived from IEFPCM calculations because Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Al-Laham, M. A.; Zakrzewski, V. G.; Ortiz, J. V.; Foresman, J. B.; Cioslowski, J.; this model is considered best for calculation of the Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; solvation energies of charged molecules.27 Nanayakkara, A.; Challacombe, M.; Peng, C. Y.; Ayala, P. A.; Chen, W.; Wong, M. W.; Andres, J. L.; Reprogle, E. S.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Binkley, J. S.; Defrees, D. J.; Baker, J.; Stewart, J. (21) Scott, A. P.; Radom, L. J. Phys. Chem. 1996, 100, 16502-16513. P.; Head-Gordon, M.; Gonzalez, C.; Pople, J. A. Gaussian 98, Revision (22) Glaser, R.; Chladny, B. S.; Hall, M. K. QCPE Bull. 1993, 13, A.7; Gaussian, Inc.: Pittsburgh, PA, 1998. 75. (17) Becke, A. D. J. Chem. Phys. 1993, 98, 5648-5652. (23) Cances, E.; Menucci, B.; Tomasi, J. J. Chem. Phys. 1997, 107, (18) Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785-789. 3032-3041. (19) Wong, M. W.; Frisch, M. J.; Wiberg, K. B. J.
Load more

Recommended publications
  • Synthesis of Small Molecule and Polymeric Systems for the Controlled Release of Sulfur Signaling Molecules
    Synthesis of Small Molecule and Polymeric Systems for the Controlled Release of Sulfur Signaling Molecules Chadwick R. Powell Dissertation submitted to the faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy In Chemistry John B. Matson, Chair Webster L. Santos Harry W. Gibson Judy S. Riffle April 25th, 2019 Blacksburg, VA Keywords: hydrogen sulfide (H2S), carbonyl sulfide (COS), persulfide, 1,6-benzyl elimination, ring-opening Copyright 2019 Synthesis of Small Molecule and Polymeric Systems for the Controlled Release of Sulfur Signaling Molecules Chadwick R. Powell ABSTRACT Hydrogen sulfide (H2S) was recognized as a critical signaling molecule in mammals nearly two decades ago. Since this discovery biologists and chemists have worked in concert to demonstrate the physiological roles of H2S as well as the therapeutic benefit of exogenous H2S delivery. As the understanding of H2S physiology has increased, the role(s) of other sulfur-containing molecules as potential players in cellular signaling and redox homeostasis has begun to emerge. This creates new and exciting challenges for chemists to synthesize compounds that release a signaling compound in response to specific, biologically relevant stimuli. Preparation of these signaling compound donor molecules will facilitate further elucidation of the complex chemical interplay within mammalian cells. To this end we report on two systems for the sustained release of H2S, as well as other sulfur signaling molecules. The first system discussed is based on the N- thiocarboxyanhydride (NTA) motif. NTAs were demonstrated to release carbonyl sulfide (COS), a potential sulfur signaling molecule, in response to biologically available nucleophiles.
    [Show full text]
  • Nomenclature of Carboxylic Acids • Select the Longest Carbon Chain Containing the Carboxyl Group
    Chapter 5 Carboxylic Acids and Esters Carboxylic Acids • Carboxylic acids are weak organic acids which Chapter 5 contain the carboxyl group (RCO2H): Carboxylic Acids and Esters O C O H O RCOOH RCO2H Chapter Objectives: O condensed ways of • Learn to recognize the carboxylic acid, ester, and related functional groups. RCOH writing the carboxyl • Learn the IUPAC system for naming carboxylic acids and esters. group a carboxylic acid C H • Learn the important physical properties of the carboxylic acids and esters. • Learn the major chemical reaction of carboxylic acids and esters, and learn how to O predict the products of ester synthesis and hydrolysis reactions. the carboxyl group • Learn some of the important properties of condensation polymers, especially the polyesters. Mr. Kevin A. Boudreaux • The tart flavor of sour-tasting foods is often caused Angelo State University CHEM 2353 Fundamentals of Organic Chemistry by the presence of carboxylic acids. Organic and Biochemistry for Today (Seager & Slabaugh) www.angelo.edu/faculty/kboudrea 2 Nomenclature of Carboxylic Acids • Select the longest carbon chain containing the carboxyl group. The -e ending of the parent alkane name is replaced by the suffix -oic acid. • The carboxyl carbon is always numbered “1” but the number is not included in the name. • Name the substituents attached to the chain in the Nomenclature of usual way. • Aromatic carboxylic acids (i.e., with a CO2H Carboxylic Acids directly connected to a benzene ring) are named after the parent compound, benzoic acid. O C OH 3
    [Show full text]
  • Optimisation Du Métabolisme Énergétique Du Soufre Chez La Bactérie Hyperthermophile Aquifex Aeolicus
    Aix-Marseille Université Ecole Doctorale des Sciences de la Vie et de la Santé Thèse de Doctorat d’Université Mention Microbiologie Clément AUSSIGNARGUES Optimisation du métabolisme énergétique du soufre chez la bactérie hyperthermophile Aquifex aeolicus Soutenue le 17 Décembre 2012 devant le jury: Pr. Frédéric BARRAS Dr. Laurent COURNAC Dr. Bruno FRANZETTI Dr. Marie-Thérèse GIUDICI-ORTICONI Dr. Anne GODFROY Dr. Marianne ILBERT Laboratoire de Bioénergétique et Ingénierie des Protéines Centre National de la Recherche Scientifique Aix-Marseille Université Ecole Doctorale des Sciences de la Vie et de la Santé Thèse de Doctorat d’Université Mention Microbiologie Clément AUSSIGNARGUES Optimisation du métabolisme énergétique du soufre chez la bactérie hyperthermophile Aquifex aeolicus Soutenue le 17 Décembre 2012 devant le jury: Pr. Frédéric BARRAS Dr. Laurent COURNAC Dr. Bruno FRANZETTI Dr. Marie-Thérèse GIUDICI-ORTICONI Dr. Anne GODFROY Dr. Marianne ILBERT Laboratoire de Bioénergétique et Ingénierie des Protéines Centre National de la Recherche Scientifique Sommaire Sommaire Introduction 2 Chapitre I- Métabolismes énergétiques du soufre 4 I) Le soufre, un élément essentiel aux multiples facettes 6 II) Le soufre utilisé comme composé énergétique 9 A) Oxydation des composés du soufre 10 1. Oxydation du sulfure d’hydrogène H2S 10 a) La Sulfure Quinone Oxydoréductase (SQR) 10 b) La flavocytochrome c sulfure déshydrogénase (FCSD) 13 2- 2. Oxydation du thiosulfate (S2O3 ) 14 a) Thiosulfate : accepteur oxydoréductase (TAOR) 14 b) Le système Sox 16 2- 3. Oxydation du sulfite (SO3 ) 20 a) Sulfite : accepteur oxydoréductase (SAOR) 21 b) Voie de l’APS 23 4. Oxydation du soufre stocké dans les globules 26 B) La réduction du soufre : soufre/polysulfure réductase 29 C) Un cas particulier : la dismutation du soufre (SOR) 33 1.
    [Show full text]
  • And Intermolecular Addition of Carboxylic Acids to Alkynes in Aqueous Media: a Review
    catalysts Review Metal-Catalyzed Intra- and Intermolecular Addition of Carboxylic Acids to Alkynes in Aqueous Media: A Review Javier Francos and Victorio Cadierno * Laboratorio de Compuestos Organometálicos y Catálisis (Unidad Asociada al CSIC), Centro de Innovación en Química Avanzada (ORFEO-CINQA), Departamento de Química Orgánica e Inorgánica, IUQOEM, Facultad de Química, Universidad de Oviedo, Julián Clavería 8, E-33006 Oviedo, Spain; [email protected] * Correspondence: [email protected]; Tel.: +34-985-103453 Received: 19 October 2017; Accepted: 2 November 2017; Published: 6 November 2017 Abstract: The metal-catalyzed addition of carboxylic acids to alkynes is a very effective tool for the synthesis of carboxylate-functionalized olefinic compounds in an atom-economical manner. Thus, a large variety of synthetically useful lactones and enol-esters can be accessed through the intra- or intermolecular versions of this process. In order to reduce the environmental impact of these reactions, considerable efforts have been devoted in recent years to the development of catalytic systems able to operate in aqueous media, which represent a real challenge taking into account the tendency of alkynes to undergo hydration in the presence of transition metals. Despite this, different Pd, Pt, Au, Cu and Ru catalysts capable of promoting the intra- and intermolecular addition of carboxylic acids to alkynes in a selective manner in aqueous environments have appeared in the literature. In this review article, an overview of this chemistry is provided. The synthesis of b-oxo esters by catalytic addition of carboxylic acids to terminal propargylic alcohols in water is also discussed. Keywords: aqueous catalysis; alkynes; carboxylic acids; alkynoic acids; hydrocarboxylation reactions; cycloisomerization reactions; enol esters; lactones; b-oxo esters 1.
    [Show full text]
  • UNDERSTANDING SULFUR BASED REDOX BIOLOGY THROUGH ADVANCEMENTS in CHEMICAL BIOLOGY by THOMAS POOLE a Dissertation Submitted to T
    UNDERSTANDING SULFUR BASED REDOX BIOLOGY THROUGH ADVANCEMENTS IN CHEMICAL BIOLOGY BY THOMAS POOLE A Dissertation Submitted to the Graduate Faculty of WAKE FOREST UNIVERSITY GRADUATE SCHOOL OF ARTS AND SCIENCES in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY Chemistry May 2017 Winston-Salem, North Carolina Approved By: S. Bruce King, Ph.D., Advisor Leslie B. Poole, Ph.D., Chair Patricia C. Dos Santos, Ph.D. Paul B. Jones, Ph.D. Mark E. Welker, Ph.D. ACKNOWLEDGEMENTS First and foremost I would like to thank professor S. Bruce King. His approach to science makes him an excellent role model that I strive to emulate. He is uniquely masterful at parsing science into important pieces and identifying the gaps and opportunities that others have missed. I thank him for the continued patience and invaluable insight as I’ve progressed through my graduate studies. This work would not have been possible without his insight and guiding suggestions. I would like to thank our collaborators who have proven invaluable in their support. Cristina Furdui has provided the knowledge, context, and biochemical support that allowed our work to be published in esteemed journals. Leslie Poole has provided the insight into redox biology and guidance towards appropriate experiments. I thank my committee members, Mark Welker and Patricia Dos Santos who have guided my graduate work from the beginning. Professor Dos Santos provided the biological perspective to evaluate my redox biology work. In addition, she helped guide the biochemical understanding required to legitimize my independent proposal. Professor Welker provided the scrutinizing eye for my early computational work and suggested validating the computational work with experimental data.
    [Show full text]
  • Carboxylic Acid Addition to Terminal Alkynes Utilizing Ammonium Tagged
    Journal of Organometallic Chemistry 883 (2019) 11e16 Contents lists available at ScienceDirect Journal of Organometallic Chemistry journal homepage: www.elsevier.com/locate/jorganchem Carboxylic acid addition to terminal alkynes utilizing ammonium tagged Hoveyda-Grubbs catalyst supported on magnetically separable core/shell silica: A highly reusable and air compatible catalytic system € € * ** Bengi Ozgün Oztürk , Didar Gürcü, Solmaz Karabulut S¸ ehitoglu Hacettepe University, Faculty of Science, Chemistry Department, 06800, Beytepe, Ankara, Turkey article info abstract Article history: In this study, the performance of ammonium tagged Hoveyda-Grubbs catalyst supported on magnetically Received 24 October 2018 separable core/shell silica gel was tested on carboxylic acid addition reactions to terminal alkynes using a Received in revised form variety of carboxylic acid derivatives under air atmosphere. The catalytic system was found to be 13 December 2018 compatible with air atmosphere and can tolerate even non-degassed solvents. The reaction parameters Accepted 10 January 2019 such as temperature, substrate/catalyst ratio and the effect of carboxylic acid on the selectivity and yield Available online 14 January 2019 of the reaction were investigated in details. The reaction of arylacetylenes with acetic acid yielded the corresponding E-isomer with conversion values up to 99% with a catalytic loading of 1% Ru. The reus- Keywords: Carboxylic acid ability of the catalyst was tested using acetic acid/benzoic acid and phenylacetylene in toluene at 85 C Alkyne under air atmosphere. The catalyst was found to be highly reusable and maintained its activity up to 11th Ruthenium run, reaching a conversion value of 83% with minimum ruthenium leaching. Reusable catalyst © 2019 Elsevier B.V.
    [Show full text]
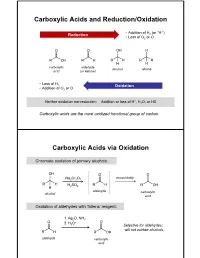
  • Carboxylic Acids and Reduction/Oxidation Carboxylic
    Carboxylic Acids and Reduction/Oxidation • Addition of H (or “H-”) Reduction 2 • Loss of O2 or O carboxylic aldehyde alcohol alkane acid (or ketone) • Loss of H 2 Oxidation • Addition of O2 or O + Neither oxidation nor reduction: Addition or loss of H , H2O, or HX Carboxylic acids are the most oxidized functional group of carbon. Carboxylic Acids via Oxidation Chromate oxidation of primary alcohols: unavoidably Na2Cr2O7 H2SO4 aldehyde carboxylic alcohol acid Oxidation of aldehydes with Tollens’ reagent: 1. Ag2O, NH3 2. H O+ 3 Selective for aldehydes; will not oxidize alcohols. aldehyde carboxylic acid Carboxylic Acids via Oxidation Oxidative cleavage of alkynes: 1. O3 2. H2O internal alkyne Oxidation of benzylic carbons: KMnO4 Purifying Carboxylic Acids by Acid-Base Extraction Acidic and basic organic molecules can be separated from other substances by manipulating their protonation state and solubility. Let’s say we run a reaction. Na2Cr2O7 + unreacted H2SO4 + Na+ 3+ We want this… + Cr(H2O)6 + organic + HSO - …but not these. side products 4 How do we isolate our desired product from the other materials, without using distillation or chromatography? Acid-Base Extraction Step 1: Remove inorganics from organics via differential solubility. a separatory (sept) funnel - Na+ HSO4 Cr(H O) 3+ H2O 2 6 CHCl3 + organic side densities: products (H2O) = 1 g/mL (CHCl3) = 1.48 g/mL A large density difference ensures the two liquids separate completely and quickly. (Much faster than, say, oil and water.) Step 2: Add basic water to deprotonate carboxylic acid, and transfer it to the aqueous phase. - Na+ HSO4 3+ discard Cr(H2O)6 H2O layer + organic + organic side side products products add discard NaOH/ H2O CHCl3 layer + organic side products Step 3: Re-acidify carboxylate to return it to organic solution.
    [Show full text]
  • Chapter 20: Carboxylic Acids and Nitriles
    CHAPTER 20 CARBOXYLIC ACIDS Based on McMurry’s Organic Chemistry, 6th edition Dr.Mohanad Al-Hachamii The Importance of Carboxylic Acids (RCO2H) Starting materials for acyl derivatives (esters, amides, and acid chlorides) Abundant in nature from oxidation of aldehydes and alcohols in metabolism Acetic acid, CH3CO2H, - vinegar Butanoic acid, CH3CH2CH2CO2H (rancid butter) Long-chain aliphatic acids from the breakdown of fats Based on McMurry, Organic Chemistry, Chapter 20, 6th edition, (c) 2003 Dr.Mohanad Al-Hachamii 2 20.1 Naming Carboxylic Acids •Carboxylic Acids, RCO2H •If derived from open-chain alkanes, replace the terminal -e of the alkane name with -oic acid •The carboxyl carbon atom is C1 Based on McMurry, Organic Chemistry, Chapter 20, 6th Dr.Mohanad Al-Hachamii edition, (c) 2003 3 Alternative Names Compounds with CO2H bonded to a ring are named using the suffix -carboxylic acid The CO2H carbon is not itself numbered in this system Use common names for formic acid (HCOOH) and acetic acid (CH3COOH) – see Table 20.1 Based on McMurry, Organic Chemistry, Chapter 20, 6th edition, (c) 2003 Dr.Mohanad Al-Hachamii 4 5 • Greek letters are used to designate the location of substituents in common names. • The carbon adjacent to the COOH is called the carbon, followed by the carbon, followed by the carbon, the carbon and so forth down the chain. • The last carbon in the chain is sometimes called the carbon. • The carbon in the common system is numbered C2 in the IUPAC system. 6 • Compounds containing two carboxy groups are called diacids. Diacids are named using the suffix –dioic acid.
    [Show full text]
  • Amidation of Carboxylic Acids with Amines by Nb2o5 As a Reusable Lewis Acid Catalyst
    Title Amidation of Carboxylic Acids with Amines by Nb2O5 as a Reusable Lewis Acid Catalyst Author(s) Ali, Md. A.; Siddiki, S. M. A. H.; Onodera, Wataru; Kon, Kenichi; Shimizu, Ken-ichi ChemCatChem, 7(21), 3555-3561 Citation https://doi.org/10.1002/cctc.201500672 Issue Date 2015-11-02 Doc URL http://hdl.handle.net/2115/63409 This is the accepted version of the following article: ChemCatChem. 7, 3555-3561(2015), which has been published in Rights final form at http://onlinelibrary.wiley.com/doi/10.1002/cctc.201500672. Type article (author version) File Information amide-wi.pdf Instructions for use Hokkaido University Collection of Scholarly and Academic Papers : HUSCAP Amidation of Carboxylic Acids with Amines by Nb2O5 as Reusable Lewis Acid Catalyst Md. A. Ali,[a] S. M. A. H. Siddiki,[b] Wataru Onodera,[a] Kenichi Kon,[a] Ken-ichi Shimizu*[a,b] [a] Catalysis Research Center, Hokkaido University, N-21, W-10, Sapporo 001-0021, Japan [b] Elements Strategy Initiative for Catalysts and Batteries, Kyoto University, Katsura, Kyoto 615-8520, Japan *Corresponding author Ken-ichi Shimizu Catalysis Research Center, Hokkaido University, N-21, W-10, Sapporo 001-0021, Japan E-mail: [email protected] Abstract: Among 28 types of heterogeneous and homogenous catalysts tested, Nb2O5 shows the highest yield for direct amidation of n-dodecanoic acid with a less reactive amine (aniline). The catalytic amidation by Nb2O5 is applicable to a wide range of carboxylic acids and amines with various functional groups, and the catalyst is reusable. Comparison of the results of the catalytic study and infrared (IR) study of the acetic acid adsorbed on the catalyst suggests that activation of carbonyl group of the carboxylic acid by Lewis acid sites on Nb2O5 is responsible for the high activity of Nb2O5.
    [Show full text]
  • Chemical Synthesis of Peptides and Peptide Thioesters Indrajeet Sharma Wayne State University
    Wayne State University Wayne State University Dissertations 1-1-2011 Chemical Synthesis Of Peptides And Peptide Thioesters Indrajeet Sharma Wayne State University Follow this and additional works at: http://digitalcommons.wayne.edu/oa_dissertations Part of the Organic Chemistry Commons Recommended Citation Sharma, Indrajeet, "Chemical Synthesis Of Peptides And Peptide Thioesters" (2011). Wayne State University Dissertations. Paper 205. This Open Access Dissertation is brought to you for free and open access by DigitalCommons@WayneState. It has been accepted for inclusion in Wayne State University Dissertations by an authorized administrator of DigitalCommons@WayneState. CHEMICAL SYNTHESIS OF PEPTIDES AND PEPTIDE THIOESTERS by INDRAJEET SHARMA DISSERTATION Submitted to the Graduate School of Wayne State University, Detroit, Michigan in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY 2011 MAJOR: CHEMISTRY (Organic) Approved by: Advisor Date DEDICATION This dissertation is dedicated to my family for their endless love and support. ii ACKNOWLEDGEMENTS First and foremost, I would like to express my deepest gratitude to my graduate advisor Professor David Crich for his advice and mentoring through all the years of my research work in his laboratories at the University of Illinois at Chicago and at Wayne State University. This work would not have reached its zenith without his unwavering guidance. He has been really supportive of my work not only with his remarkable knowledge and painstaking guidance, but also with his valuable suggestions and constant encouragement. I wish to thank my committee members Professor Zhongwu Guo, Professor Ashok S. Bhagwat, and Professor Steven J. Sucheck for their valuable time and suggestions to this dissertation and defense.
    [Show full text]
  • Synthesis of New Linear Polymers Containing Thiocarbonyl Groups: Polyaddition of Dicarbothioic Acid to Diolefins
    Polymer Journal, Vol. 26, No. 1, pp 49-59 (1994) Synthesis of New Linear Polymers Containing Thiocarbonyl Groups: Polyaddition of Dicarbothioic Acid to Diolefins Eiichi KOBAYASHI,* Kazuyoshi TENDO, Masato KATO, and Sadahito AoSHIMA Department of Industrial Chemistry, Faculty of Science and Technology, Science University of Tokyo, Noda, Chiba 278, Japan (Received May 24, 1993) ABSTRACT: The polyaddition of 1,4-benzenedicarbothioic acid to 1,4-divinylbenzene or 1,4-diisopropenylbenzene was carried out at 70°C in toluene under a nitrogen atmosphere by radical mode such as by addition of AIBN or UV irradiation. Both diolefin compounds gave polymers in a 90% yield. The polymer obtained from I ,4-diisopropenylbenzene was soluble in chloroform, and the molecular weight of the polymer (Mw) was 40000. On the other hand, the polymer obtained from 1,4-divinylbenzene was partly soluble in conventional organic solvents, possibly due to a cross linkage formation by a pendant vinyl group. The model addition reaction of thiobenzoic acid to styrene gave a by-product ca. 8% being the I : 2 adduct with respect to thiobenzoic acid and styrene. Alkali hydrolysis of both polymers was investigated to confirm the cross linkage structures in the polymers. KEY WORDS Polyaddition / Polythioester / Addition Reaction/ Hydrolysis / 1,4-Benzenedicarbothioic Acid / 1,4-Divinylbenzene / 1,4-Diisoprope­ nylbenzene / Thiobenzoic Acid/ Styrene/ oc-Methylstyrene / Addition reactions of carbothioic acids to (nb8 = 1.81) and exhibited the reversible phase olefins occur easily and are used to prepare transition by heat mode. various thioesters or polythioesters. For CH2=CH-<Q)--CH=CH2 + HS-<Q)--SH R or UV example, Ipatieff et al.
    [Show full text]
  • REVIEW ARTICLE View Journal | View Issue
    Chem Soc Rev View Article Online REVIEW ARTICLE View Journal | View Issue Developments and recent advancements in the field of endogenous amino acid selective bond Cite this: Chem. Soc. Rev., 2015, 44,5495 forming reactions for bioconjugation Oleksandr Konievab and Alain Wagner*a Bioconjugation methodologies have proven to play a central enabling role in the recent development of biotherapeutics and chemical biology approaches. Recent endeavours in these fields shed light on unprecedented chemical challenges to attain bioselectivity, biocompatibility, and biostability required by modern applications. In this review the current developments in various techniques of selective bond Received 19th January 2015 forming reactions of proteins and peptides were highlighted. The utility of each endogenous amino DOI: 10.1039/c5cs00048c acid-selective conjugation methodology in the fields of biology and protein science has been surveyed with emphasis on the most relevant among reported transformations; selectivity and practical use have www.rsc.org/chemsocrev been discussed. Creative Commons Attribution 3.0 Unported Licence. Contents 1.5 Histidine 1.5.1 Epoxides Introduction 1.5.2 Complexes with transition metals 1 In-chain conjugation 1.5.3 Michael addition 1.1 Lysine 1.5.4 Miscellaneous histidine-selective reagents 1.1.1 Isocyanates and isothiocyanates 1.6 Tyrosine This article is licensed under a 1.1.2 Activated esters 1.6.1 O-Derivatisation 1.1.3 Reductive amination of aldehydes 1.6.2 O-Oxidatiove coupling 1.1.4 Sulfonyl halides and sulfonates 1.6.3 Diazonium reagents Open Access Article. Published on 22 May 2015. Downloaded 10/8/2021 1:59:09 PM.
    [Show full text]