DOCSLIB.ORG

Bayesian Statistics for Genetics Lecture 4: Linear Regression

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bayesian Statistics for Genetics Lecture 4: Linear Regression Bayesian Statistics for Genetics Lecture 4: Linear Regression Ken Rice Swiss Institute in Statistical Genetics September, 2017 Regression models: overview How does an outcome Y vary as a function of x = fx1; : : : ; xpg? • What are the effect sizes? • What is the effect of x1, in observations that have the same x2; x3; :::xp (a.k.a. \keeping these covariates constant")? • Can we predict Y as a function of x? These questions can be assessed via a regression model p(yjx). 4.1 Regression models: overview Parameters in a regression model can be estimated from data: 0 1 y1 x1;1 ··· x1;p B . C @ . A yn xn;1 ··· xn;p The data are often expressed in matrix/vector form: 0 1 0 1 0 1 y1 x1 x1;1 ··· x1;p B . C B . C B . C y = @ . A X = @ . A = @ . A yn xn xn;1 ··· xn;p 4.2 FTO example: design FTO gene is hypothesized to be involved in growth and obesity. Experimental design: • 10 fto + =− mice • 10 fto − =− mice • Mice are sacrificed at the end of 1-5 weeks of age. • Two mice in each group are sacrificed at each age. 4.3 FTO example: data ● ● 25 ● fto−/− ● ● fto+/− 20 ● ● ● 15 ● ● ● ● weight (g) weight ● ● ● ● 10 ● ● ● ● 5 ● 1 2 3 4 5 age (weeks) 4.4 FTO example: analysis • y = weight • xg = indicator of fto heterozygote 2 f0; 1g = number of \+" alleles • xa = age in weeks 2 f1; 2; 3; 4; 5g How can we estimate p(yjxg; xa)? Cell means model: genotype age −=− θ0;1 θ0;2 θ0;3 θ0;4 θ0;5 +=− θ1;1 θ1;2 θ1;3 θ1;4 θ1;5 Problem: 10 parameters { only two observations per cell 4.5 Linear regression Solution: Assume smoothness as a function of age. For each group, y = α0 + α1xa + . This is a linear regression model. Linearity means \linear in the parameters", i.e. several covariates, each multiplied by corresponding α, and added. A more complex model might assume e.g. 2 3 y = α0 + α1xa + α2xa + α3xa + , { but this is still a linear regression model, even with age2, age3 terms. 4.6 Multiple linear regression With enough variables, we can describe the regressions for both groups simultaneously: Yi = β1xi;1 + β2xi;2 + β3xi;3 + β4xi;4 + i ; where xi;1 = 1 for each subject i xi;2 = 0 if subject i is homozygous, 1 if heterozygous xi;3 = age of subject i xi;4 = xi;2 × xi;3 Note that under this model, E[ Y jx; ] = β1 + β3 × age if x2 = 0, and E[ Y jx ] = (β1 + β2) + (β3 + β4) × age if x2 = 1. 4.7 Multiple linear regression For graphical thinkers... β3 = 0 β4 = 0 β2 = 0 β4 = 0 ● ● ● ● 25 ● ● 20 ● ● ● ● ● ● 15 ● ● ● ● weight ● ● ● ● ● ● ● ● ● ● ● ● 10 ● ● ● ● ● ● ● ● 5 ● ● β4 = 0 ● ● ● ● 25 ● ● 20 ● ● ● ● ● ● 15 ● ● ● ● weight ● ● ● ● ● ● ● ● ● ● ● ● 10 ● ● ● ● ● ● ● ● 5 ● ● 1 2 3 4 5 1 2 3 4 5 age age 4.8 Normal linear regression How does each Yi vary around its mean E[ Yijββ; xi ]; ? T Yi = β xi + i 2 1; : : : ; n ∼ i.i.d. normal(0; σ ): This assumption of Normal errors specifies the likelihood: n 2 Y 2 p(y1; : : : ; ynjx1;::: xn; ββ; σ ) = p(yijxi; ββ; σ ) i=1 1 n = (2 2)−n=2exp X ( T )2 πσ {− 2 yi − β xi g: 2σ i=1 Note: in large(r) sample sizes, analysis is \robust" to the Normality assumption|but here we rely on the mean being linear in the x's, and on the i's variance being constant with respect to x. 4.9 Matrix form T • Let y be the n-dimensional column vector (y1; : : : ; yn) ; • Let X be the n × p matrix whose ith row is xi Then the normal regression model is that yjX; ββ; σ2 ∼ multivariate normal (Xββ; σ2I); where I is the p × p identity matrix and 0 x ! 1 1 0 β 1 0 β x + ··· + β x 1 0 Y jββ; x 1 B C 1 1 1;1 p 1;p E 1 1 B x2 ! C B . C B . C B . C Xβ = B . C @ . A = @ . A = @ . A : @ . A βp β1xn;1 + ··· + βpxn;p EYnjββ; xn xn ! 4.10 Ordinary least squares estimation What values of β are consistent with our data y;X? Recall 1 n ( 2) = (2 2)−n=2exp X ( T )2 p y1; : : : ; ynjx1;::: xn; ββ; σ πσ {− 2 yi−β xi g: 2σ i=1 P T 2 This is big when SSR(β) = (yi − β xi) is small { where we define n X T 2 T SSR(β) = (yi − β xi) = (y − Xβ) (y − Xβ) i=1 = yT y − 2βTXT y + βTXTXβ : What value of β makes this the smallest, i.e. gives fitted values closest to the outcomes y1; y2; :::yn? 4.11 OLS: with calculus `Recall' that... 1. a minimum of a function g(z) occurs at a value z such that d dzg(z) = 0; 2. the derivative of g(z) = az is a and the derivative of g(z) = bz2 is 2bz. Doing this for SSR... d d SSR(β) = yT y − 2βTXT y + βTXTXβ dββ dββ = −2XT y + 2XTXβ ; d and so SSR(β) = 0 , −2XT y + 2XTXβ = 0 dββ , XTXβ = XT y , β = (XTX)−1XT y : ^ T −1 T βols = (X X) X y is the Ordinary Least Squares (OLS) estimator of β. 4.12 OLS: without calculus The calculus-free, algebra-heavy version { which relies on knowing the answer in advance! T −1 T ^ Writing Π = X(X X) X , and noting that X = ΠX and Xβols = Πy; (y − Xβ)T (y − Xβ) = (y − Πy + Πy − Xβ)T (y − Πy + Πy − Xβ) ^ T ^ = ((I − Π)y + Π(βols − β)) ((I − Π)y + Π(βols − β)) T ^ T ^ = y (I − Π)y + (βols − β) Π(βols − β); because all the `cross terms' with Π and I − Π are zero. Hence the value of β that minimizes the SSR { for a given set ^ of data { is βols. 4.13 OLS: using R ### OLS estimate > beta.ols <- solve( t(X)%*%X )%*%t(X)%*%y > beta.ols [,1] (Intercept) -0.06821632 xg 2.94485495 xa 2.84420729 xg:xa 1.72947648 ### or less painfully, using lm() > fit.ols<-lm( y~ xg*xa ) > coef( summary(fit.ols) ) Estimate Std. Error t value Pr(>|t|) (Intercept) -0.06821632 1.4222970 -0.04796208 9.623401e-01 xg 2.94485495 2.0114316 1.46405917 1.625482e-01 xa 2.84420729 0.4288387 6.63234803 5.760923e-06 xg:xa 1.72947648 0.6064695 2.85171239 1.154001e-02 4.14 OLS: using R ● ● ● ● ● ● ● ● weight ● ● ● ● ● ● ● ● ● ● ● 1 2 3 4 5 age > coef( summary(fit.ols) ) Estimate Std. Error t value Pr(>|t|) (Intercept) -0.06821632 1.4222970 -0.04796208 9.623401e-01 xg 2.94485495 2.0114316 1.46405917 1.625482e-01 xa 2.84420729 0.4288387 6.63234803 5.760923e-06 xg:xa 1.72947648 0.6064695 2.85171239 1.154001e-02 4.15 Bayesian inference for regression models yi = β1xi;1 + ··· + βpxi;p + i Motivation: • Incorporating prior information • Posterior probability statements: P[ βj > 0jy;X ] • OLS tends to overfit when p is large, Bayes' use of prior tends to make it more conservative { as we'll see • Model selection and averaging (more later) 4.16 Prior and posterior distribution prior β ∼ mvn(β0; Σ0) sampling model y ∼ mvn(Xββ; σ2I) posterior βjy;X ∼ mvn(βn; Σn) where 2 −1 T 2 −1 Σn = Varβjy;X; σ = (Σ0 + X X/σ ) 2 −1 T 2 −1 −1 T 2 βn = Eβjy;X; σ = (Σ0 + X X/σ ) (Σ0 β0 + X y/σ ): Notice: −1 T 2 ^ • If Σ0 X X/σ , then βn ≈ βols −1 T 2 • If Σ0 X X/σ , then βn ≈ β0 4.17 The g-prior How to pick β0; Σ0? A classical suggestion (Zellner, 1986) uses the g-prior: β ∼ mvn(0; gσ2(XTX)−1) ^ Idea: The variance of the OLS estimate βols is σ2 Varβ^ = σ2(XTX)−1 = (XTX=n)−1 ols n This is (roughly) the uncertainty in β from n observations. σ2 Varβ = gσ2(XTX)−1 = (XTX=n)−1 gprior n=g The g-prior can roughly be viewed as the uncertainty from n=g observations. For example, g = n means the prior has the same amount of info as 1 observation { so (roughly!) not much, in a large study. 4.18 Posterior distributions under the g-prior After some algebra, it turns out that 2 fβjy;X; σ g ∼ mvn(βn; Σn); 2 g 2 T −1 where Σn = Var[βjy;X; σ ] = σ (X X) g + 1 2 g T −1 T βn = E[βjy;X; σ ] = (X X) X y g + 1 Notes: g ^ • The posterior mean estimate βn is simply g+1βols. g ^ • The posterior variance of β is simply g+1Varβols. • g shrinks the coefficients towards 0 and can prevent overfit- ting to the data • If g = n, then as n increases, inference approximates that ^ using βols. 4.19 Monte Carlo simulation What about the error variance σ2? It's rarely known exactly, so more realistic to allow for uncertainty with a prior... 2 2 prior1 /σ ∼ gamma(ν0=2; ν0σ0=2) sampling model y ∼ mvn(Xββ; σ2I) 2 2 posterior1 /σ jy;X ∼ gamma([ν0 + n]=2; [ν0σ0 + SSRg]=2) where SSRg is somewhat complicated. Simulating the joint posterior distribution: joint distribution p(σ2; βjy;X) = p(σ2jy;X) × p(βjy;X; σ2) simulation fσ2; βg ∼ p(σ2; βjy;X) , σ2 ∼ p(σ2jy;X); β ∼ p(βjy;X; σ2) To simulate fσ2; βg ∼ p(σ2; βjy;X), • First simulate σ2 from p(σ2jy;X) • Use this σ2 to simulate β from p(βjy;X; σ2) Repeat 1000's of times to obtain MC samples: fσ2; βg(1);:::; fσ2; βg(S).
Load more

Recommended publications
  • DSA 5403 Bayesian Statistics: an Advancing Introduction 16 Units – Each Unit a Week’S Work
    DSA 5403 Bayesian Statistics: An Advancing Introduction 16 units – each unit a week’s work. The following are the contents of the course divided into chapters of the book Doing Bayesian Data Analysis . by John Kruschke. The course is structured around the above book but will be embellished with more theoretical content as needed. The book can be obtained from the library : http://www.sciencedirect.com/science/book/9780124058880 Topics: This is divided into three parts From the book: “Part I The basics: models, probability, Bayes' rule and r: Introduction: credibility, models, and parameters; The R programming language; What is this stuff called probability?; Bayes' rule Part II All the fundamentals applied to inferring a binomial probability: Inferring a binomial probability via exact mathematical analysis; Markov chain Monte C arlo; J AG S ; Hierarchical models; Model comparison and hierarchical modeling; Null hypothesis significance testing; Bayesian approaches to testing a point ("Null") hypothesis; G oals, power, and sample size; S tan Part III The generalized linear model: Overview of the generalized linear model; Metric-predicted variable on one or two groups; Metric predicted variable with one metric predictor; Metric predicted variable with multiple metric predictors; Metric predicted variable with one nominal predictor; Metric predicted variable with multiple nominal predictors; Dichotomous predicted variable; Nominal predicted variable; Ordinal predicted variable; C ount predicted variable; Tools in the trunk” Part 1: The Basics: Models, Probability, Bayes’ Rule and R Unit 1 Chapter 1, 2 Credibility, Models, and Parameters, • Derivation of Bayes’ rule • Re-allocation of probability • The steps of Bayesian data analysis • Classical use of Bayes’ rule o Testing – false positives etc o Definitions of prior, likelihood, evidence and posterior Unit 2 Chapter 3 The R language • Get the software • Variables types • Loading data • Functions • Plots Unit 3 Chapter 4 Probability distributions.
    [Show full text]
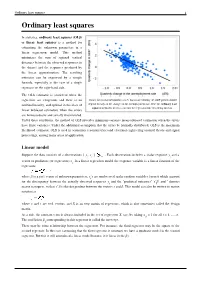
  • Ordinary Least Squares 1 Ordinary Least Squares
    Ordinary least squares 1 Ordinary least squares In statistics, ordinary least squares (OLS) or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear approximation. The resulting estimator can be expressed by a simple formula, especially in the case of a single regressor on the right-hand side. The OLS estimator is consistent when the regressors are exogenous and there is no Okun's law in macroeconomics states that in an economy the GDP growth should multicollinearity, and optimal in the class of depend linearly on the changes in the unemployment rate. Here the ordinary least squares method is used to construct the regression line describing this law. linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Under these conditions, the method of OLS provides minimum-variance mean-unbiased estimation when the errors have finite variances. Under the additional assumption that the errors be normally distributed, OLS is the maximum likelihood estimator. OLS is used in economics (econometrics) and electrical engineering (control theory and signal processing), among many areas of application. Linear model Suppose the data consists of n observations { y , x } . Each observation includes a scalar response y and a i i i vector of predictors (or regressors) x . In a linear regression model the response variable is a linear function of the i regressors: where β is a p×1 vector of unknown parameters; ε 's are unobserved scalar random variables (errors) which account i for the discrepancy between the actually observed responses y and the "predicted outcomes" x′ β; and ′ denotes i i matrix transpose, so that x′ β is the dot product between the vectors x and β.
    [Show full text]
  • Ordinary Least Squares: the Univariate Case
    Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Ordinary Least Squares: the univariate case Clément de Chaisemartin Majeure Economie September 2011 Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises 1 Introduction 2 The OLS method Objective and principles of OLS Deriving the OLS estimates Do OLS keep their promises ? 3 The linear causal model Assumptions Identification and estimation Limits 4 A simulation & applications OLS do not always yield good estimates... But things can be improved... Empirical applications 5 Conclusion and exercises Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objectives Objective 1 : to make the best possible guess on a variable Y based on X . Find a function of X which yields good predictions for Y . Given cigarette prices, what will be cigarettes sales in September 2010 in France ? Objective 2 : to determine the causal mechanism by which X influences Y . Cetebus paribus type of analysis. Everything else being equal, how a change in X affects Y ? By how much one more year of education increases an individual’s wage ? By how much the hiring of 1 000 more policemen would decrease the crime rate in Paris ? The tool we use = a data set, in which we have the wages and number of years of education of N individuals. Clément de Chaisemartin Ordinary Least Squares Introduction The OLS method The linear causal model A simulation & applications Conclusion and exercises Objective and principles of OLS What we have and what we want For each individual in our data set we observe his wage and his number of years of education.
    [Show full text]
  • Chapter 2: Ordinary Least Squares Regression
    Chapter 2: Ordinary Least Squares In this chapter: 1. Running a simple regression for weight/height example (UE 2.1.4) 2. Contents of the EViews equation window 3. Creating a workfile for the demand for beef example (UE, Table 2.2, p. 45) 4. Importing data from a spreadsheet file named Beef 2.xls 5. Using EViews to estimate a multiple regression model of beef demand (UE 2.2.3) 6. Exercises Ordinary Least Squares (OLS) regression is the core of econometric analysis. While it is important to calculate estimated regression coefficients without the aid of a regression program one time in order to better understand how OLS works (see UE, Table 2.1, p.41), easy access to regression programs makes it unnecessary for everyday analysis.1 In this chapter, we will estimate simple and multivariate regression models in order to pinpoint where the regression statistics discussed throughout the text are found in the EViews program output. Begin by opening the EViews program and opening the workfile named htwt1.wf1 (this is the file of student height and weight that was created and saved in Chapter 1). Running a simple regression for weight/height example (UE 2.1.4): Regression estimation in EViews is performed using the equation object. To create an equation object in EViews, follow these steps: Step 1. Open the EViews workfile named htwt1.wf1 by selecting File/Open/Workfile on the main menu bar and click on the file name. Step 2. Select Objects/New Object/Equation from the workfile menu.2 Step 3.
    [Show full text]
  • The Bayesian Approach to Statistics
    THE BAYESIAN APPROACH TO STATISTICS ANTHONY O’HAGAN INTRODUCTION the true nature of scientific reasoning. The fi- nal section addresses various features of modern By far the most widely taught and used statisti- Bayesian methods that provide some explanation for the rapid increase in their adoption since the cal methods in practice are those of the frequen- 1980s. tist school. The ideas of frequentist inference, as set out in Chapter 5 of this book, rest on the frequency definition of probability (Chapter 2), BAYESIAN INFERENCE and were developed in the first half of the 20th century. This chapter concerns a radically differ- We first present the basic procedures of Bayesian ent approach to statistics, the Bayesian approach, inference. which depends instead on the subjective defini- tion of probability (Chapter 3). In some respects, Bayesian methods are older than frequentist ones, Bayes’s Theorem and the Nature of Learning having been the basis of very early statistical rea- Bayesian inference is a process of learning soning as far back as the 18th century. Bayesian from data. To give substance to this statement, statistics as it is now understood, however, dates we need to identify who is doing the learning and back to the 1950s, with subsequent development what they are learning about. in the second half of the 20th century. Over that time, the Bayesian approach has steadily gained Terms and Notation ground, and is now recognized as a legitimate al- ternative to the frequentist approach. The person doing the learning is an individual This chapter is organized into three sections.
    [Show full text]
  • Posterior Propriety and Admissibility of Hyperpriors in Normal
    The Annals of Statistics 2005, Vol. 33, No. 2, 606–646 DOI: 10.1214/009053605000000075 c Institute of Mathematical Statistics, 2005 POSTERIOR PROPRIETY AND ADMISSIBILITY OF HYPERPRIORS IN NORMAL HIERARCHICAL MODELS1 By James O. Berger, William Strawderman and Dejun Tang Duke University and SAMSI, Rutgers University and Novartis Pharmaceuticals Hierarchical modeling is wonderful and here to stay, but hyper- parameter priors are often chosen in a casual fashion. Unfortunately, as the number of hyperparameters grows, the effects of casual choices can multiply, leading to considerably inferior performance. As an ex- treme, but not uncommon, example use of the wrong hyperparameter priors can even lead to impropriety of the posterior. For exchangeable hierarchical multivariate normal models, we first determine when a standard class of hierarchical priors results in proper or improper posteriors. We next determine which elements of this class lead to admissible estimators of the mean under quadratic loss; such considerations provide one useful guideline for choice among hierarchical priors. Finally, computational issues with the resulting posterior distributions are addressed. 1. Introduction. 1.1. The model and the problems. Consider the block multivariate nor- mal situation (sometimes called the “matrix of means problem”) specified by the following hierarchical Bayesian model: (1) X ∼ Np(θ, I), θ ∼ Np(B, Σπ), where X1 θ1 X2 θ2 Xp×1 = . , θp×1 = . , arXiv:math/0505605v1 [math.ST] 27 May 2005 . X θ m m Received February 2004; revised July 2004. 1Supported by NSF Grants DMS-98-02261 and DMS-01-03265. AMS 2000 subject classifications. Primary 62C15; secondary 62F15. Key words and phrases. Covariance matrix, quadratic loss, frequentist risk, posterior impropriety, objective priors, Markov chain Monte Carlo.
    [Show full text]
  • The Deviance Information Criterion: 12 Years On
    J. R. Statist. Soc. B (2014) The deviance information criterion: 12 years on David J. Spiegelhalter, University of Cambridge, UK Nicola G. Best, Imperial College School of Public Health, London, UK Bradley P. Carlin University of Minnesota, Minneapolis, USA and Angelika van der Linde Bremen, Germany [Presented to The Royal Statistical Society at its annual conference in a session organized by the Research Section on Tuesday, September 3rd, 2013, Professor G. A.Young in the Chair ] Summary.The essentials of our paper of 2002 are briefly summarized and compared with other criteria for model comparison. After some comments on the paper’s reception and influence, we consider criticisms and proposals for improvement made by us and others. Keywords: Bayesian; Model comparison; Prediction 1. Some background to model comparison Suppose that we have a given set of candidate models, and we would like a criterion to assess which is ‘better’ in a defined sense. Assume that a model for observed data y postulates a density p.y|θ/ (which may include covariates etc.), and call D.θ/ =−2log{p.y|θ/} the deviance, here considered as a function of θ. Classical model choice uses hypothesis testing for comparing nested models, e.g. the deviance (likelihood ratio) test in generalized linear models. For non- nested models, alternatives include the Akaike information criterion AIC =−2log{p.y|θˆ/} + 2k where θˆ is the maximum likelihood estimate and k is the number of parameters in the model (dimension of Θ). AIC is built with the aim of favouring models that are likely to make good predictions.
    [Show full text]
  • Time-Series Regression and Generalized Least Squares in R*
    Time-Series Regression and Generalized Least Squares in R* An Appendix to An R Companion to Applied Regression, third edition John Fox & Sanford Weisberg last revision: 2018-09-26 Abstract Generalized least-squares (GLS) regression extends ordinary least-squares (OLS) estimation of the normal linear model by providing for possibly unequal error variances and for correlations between different errors. A common application of GLS estimation is to time-series regression, in which it is generally implausible to assume that errors are independent. This appendix to Fox and Weisberg (2019) briefly reviews GLS estimation and demonstrates its application to time-series data using the gls() function in the nlme package, which is part of the standard R distribution. 1 Generalized Least Squares In the standard linear model (for example, in Chapter 4 of the R Companion), E(yjX) = Xβ or, equivalently y = Xβ + " where y is the n×1 response vector; X is an n×k +1 model matrix, typically with an initial column of 1s for the regression constant; β is a k + 1 ×1 vector of regression coefficients to estimate; and " is 2 an n×1 vector of errors. Assuming that " ∼ Nn(0; σ In), or at least that the errors are uncorrelated and equally variable, leads to the familiar ordinary-least-squares (OLS) estimator of β, 0 −1 0 bOLS = (X X) X y with covariance matrix 2 0 −1 Var(bOLS) = σ (X X) More generally, we can assume that " ∼ Nn(0; Σ), where the error covariance matrix Σ is sym- metric and positive-definite. Different diagonal entries in Σ error variances that are not necessarily all equal, while nonzero off-diagonal entries correspond to correlated errors.
    [Show full text]
  • A Widely Applicable Bayesian Information Criterion
    JournalofMachineLearningResearch14(2013)867-897 Submitted 8/12; Revised 2/13; Published 3/13 A Widely Applicable Bayesian Information Criterion Sumio Watanabe [email protected] Department of Computational Intelligence and Systems Science Tokyo Institute of Technology Mailbox G5-19, 4259 Nagatsuta, Midori-ku Yokohama, Japan 226-8502 Editor: Manfred Opper Abstract A statistical model or a learning machine is called regular if the map taking a parameter to a prob- ability distribution is one-to-one and if its Fisher information matrix is always positive definite. If otherwise, it is called singular. In regular statistical models, the Bayes free energy, which is defined by the minus logarithm of Bayes marginal likelihood, can be asymptotically approximated by the Schwarz Bayes information criterion (BIC), whereas in singular models such approximation does not hold. Recently, it was proved that the Bayes free energy of a singular model is asymptotically given by a generalized formula using a birational invariant, the real log canonical threshold (RLCT), instead of half the number of parameters in BIC. Theoretical values of RLCTs in several statistical models are now being discovered based on algebraic geometrical methodology. However, it has been difficult to estimate the Bayes free energy using only training samples, because an RLCT depends on an unknown true distribution. In the present paper, we define a widely applicable Bayesian information criterion (WBIC) by the average log likelihood function over the posterior distribution with the inverse temperature 1/logn, where n is the number of training samples. We mathematically prove that WBIC has the same asymptotic expansion as the Bayes free energy, even if a statistical model is singular for or unrealizable by a statistical model.
    [Show full text]
  • Chapter 2 Simple Linear Regression Analysis the Simple
    Chapter 2 Simple Linear Regression Analysis The simple linear regression model We consider the modelling between the dependent and one independent variable. When there is only one independent variable in the linear regression model, the model is generally termed as a simple linear regression model. When there are more than one independent variables in the model, then the linear model is termed as the multiple linear regression model. The linear model Consider a simple linear regression model yX01 where y is termed as the dependent or study variable and X is termed as the independent or explanatory variable. The terms 0 and 1 are the parameters of the model. The parameter 0 is termed as an intercept term, and the parameter 1 is termed as the slope parameter. These parameters are usually called as regression coefficients. The unobservable error component accounts for the failure of data to lie on the straight line and represents the difference between the true and observed realization of y . There can be several reasons for such difference, e.g., the effect of all deleted variables in the model, variables may be qualitative, inherent randomness in the observations etc. We assume that is observed as independent and identically distributed random variable with mean zero and constant variance 2 . Later, we will additionally assume that is normally distributed. The independent variables are viewed as controlled by the experimenter, so it is considered as non-stochastic whereas y is viewed as a random variable with Ey()01 X and Var() y 2 . Sometimes X can also be a random variable.
    [Show full text]
  • Bayes Theorem and Its Recent Applications
    BAYES THEOREM AND ITS RECENT APPLICATIONS Nicholas Stylianides Eleni Kontou March 2020 Abstract Individuals who have studied maths to a specific level have come across Bayes’ Theorem or Bayes Formula. Bayes’ Theorem has many applications in areas such as mathematics, medicine, finance, marketing, engineering and many other. This paper covers Bayes’ Theorem at a basic level and explores how the formula was derived. We also, look at some extended forms of the formula and give an explicit example. Lastly, we discuss recent applications of Bayes’ Theorem in valuating depression and predicting water quality conditions. The goal of this expository paper is to break down the interesting topic of Bayes’ Theorem to a basic level which can be easily understood by a wide audience. What is Bayes Theorem? Thomas Bayes was an 18th-century British mathematician who developed a mathematical formula to calculate conditional probability in order to provide a way to re-examine current expectations. This mathematical formula is well known as Bayes Theorem or Bayes’ rule or Bayes’ Law. It is also the basis of a whole field of statistics known as Bayesian Statistics. For example, in finance, Bayes’ Theorem can be utilized to rate the risk of loaning cash to possible borrowers. The formula for Bayes’ Theorem is: [1] P(A) =The probability of A occurring P(B) = The probability of B occurring P(A|B) = The probability of A given B P(B|A) = The probability of B given A P(A∩B) = The probability of both A and B occurring MA3517 Mathematics Research Journal @Nicholas Stylianides, Eleni Kontou Bayes’ Theorem: , a $% &((!) > 0 %,- .// Proof: From Bayes’ Formula: (1) From the Total Probability (2) Theorem: Substituting equation (2) into equation (1) we obtain .
    [Show full text]
  • Regression Analysis
    Regression Analysis Terminology Independent (Exogenous) Variable – Our X value(s), they are variables that are used to explain our y variable. They are not linearly dependent upon other variables in our model to get their value. X1 is not a function of Y nor is it a linear function of any of the other X variables. 2 Note, this does not exclude X2=X1 as another independent variable as X2 and X1 are not linear combinations of each other. Dependent (Endogenous) Variable – Our Y value, it is the value we are trying to explain as, hypothetically, a function of the other variables. Its value is determined by or dependent upon the values of other variables. Error Term – Our ε, they are the portion of the dependent variable that is random, unexplained by any independent variable. Intercept Term – Our α, from the equation of a line, it is the y-value where the best-fit line intercepts the y-axis. It is the estimated value of the dependent variable given the independent variable(s) has(have) a value of zero. Coefficient(s) – Our β(s), this is the number in front of the independent variable(s) in the model below that relates how much a one unit change in the independent variable is estimated to change the value of the dependent variable. Standard Error – This number is an estimate of the standard deviation of the coefficient. Essentially, it measures the variability in our estimate of the coefficient. Lower standard errors lead to more confidence of the estimate because the lower the standard error, the closer to the estimated coefficient is the true coefficient.
    [Show full text]