DOCSLIB.ORG

Title Pages.Pmd

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Title Pages.Pmd © Government of Tamilnadu First Edition-2003 Reprint - 2005 Chairperson Dr. K. SRINIVASAN Reader in Mathematics Presidency College (Autonomous) Chennai - 600 005. Reviewers Prof. (Mrs.) SHIELA BOSE Thiru M.K. SUBRAMANIAN Head Department of Mathematics, Deputy Director, Lady Willingdon Institute of Directorate of Teacher Education, Advanced Study in Education, Research and Training, Chennai - 600 005. Chennai - 600 006. Authors Thiru G. GNANASUNDARAM Thiru M. PALANIVASAN P.G. Teacher, P.G. Teacher, S.S.V. Higher Secondary School, I.C.F. Higher Secondary School, Park Town, Chennai - 600 003. Chennai - 600 038. Thiru P. NAGARAJAN Thiru T. KATHIRVEL B.T. Assistant, Assistant Headmaster, B.R. Govt. High School, Govt. Higher Secondary School, Puzhal-600 066. Arumbakkam, Tiruvallur Dt. Chennai - 600 106. Price : Rs. 33-00 This book has been prepared by The Directorate of School Education on behalf of the Government of Tamilnadu This book has been printed on 60 G.S.M. Paper Printed by Offset at : CONTENTS Page No. 1. NUMBER WORK 1 1.1 Numbers – Revision 1 1.1.1 Natural Numbers and Whole Numbers 1.1.2 Face value and Place value 1.1.3 Expanded form 1.2 Four fundamental operations on Whole numbers 5 1.2.1 Addition 1.2.2 Subtraction 1.2.3 Multipliction 1.2.4 Division 1.3 Number patterns 13 1.3.1 Divisors, Factors and Multiples 1.3.2 Even and Odd numbers 1.3.3 Prime and Composite numbers 1.4 Large numbers in Exponential form 17 1.5 Tests of divisibility – Revision 20 1.6 Greatest common divisor and Least common multiple 23 1.7 Integers 28 1.7.1 Directed numbers 1.7.2 Integers and order in number line 1.7.3 Addition and Subtraction of integers 1.7.4 Multiplication of integers 1.7.5 Division of integers 1.8 Fractions 41 1.8.1 Fractions – Revision 1.8.2 Addition and Subtraction on Fractions 1.8.3 Multiplication and Division on Fractions 1.9 Decimal numbers 53 1.9.1 Decimal form of fractions 1.9.2 Four fundamental operations on decimals 2. EVERYDAY ARITHMETIC 65 2.1 Ratio and Proportion 65 2.1.1 Ratio formation 2.1.2 Comparison of ratios 2.1.3 Proportion formation 2.1.4 Proportion – Applications 2.1.5 Direct variation 2.2 Percentage 77 2.2.1 Percentages, Fractions and Decimals – Relationship 2.2.2 Profit and Loss 2.2.3 Profit and Loss percentage 2.3 Shopping 84 2.3.1 Verification of bill amount 2.3.2 Preparation of a bill 2.4 Finance 90 2.4.1 Simple Interest (Unitary Method) 2.4.2 Formula for Simple Interest 3. MEASUREMENTS 95 3.1 Metric measures 95 3.1.1 Linear measures (measures of length) 3.1.2 Measures of weight 3.1.3 Measures of capacity 3.1.4 Addition and Subtraction in metric measures 3.1.5 Multiplication and Division in metric measures 3.1.6 Measures of area 3.1.7 Measures of volume 3.2 Measures of Time 111 3.2.1 Ordinary time and Railway time; Ordinary year and Leap year 3.2.2 Calculating number of days. 3.2.3 Finding the day of the week 3.3 Area and Perimeter 121 3.3.1 Area and perimeter of a square 3.3.2 Area and perimeter of a rectangle 3.3.3 Area and perimeter of a right angled triangle 3.3.4 Area of Four walls 4. ALGEBRA 137 4.1 Introduction 137 4.2 Mathematical statements 137 4.3 Place holders 138 4.4 Literals 140 4.5 Constants and Variables 141 4.6 Power (or Exponent or Index) of a variable 143 4.7 Coefficients 144 4.8 Terms 145 4.9 Addition and Subtraction of terms 147 5. GEOMETRY 151 5.1 Basic geometrical concepts 151 5.1.1 Point 5.1.2 Line 5.1.3 Ray 5.1.4 Line segment 5.1.5 Plane 5.2 Relationship between points and lines 155 5.2.1 Concurrent lines 5.2.2 Collinear points 5.2.3 Intersecting and Parallel lines 5.3 Angles 159 5.3.1 Angle and measure of an angle 5.3.2 Types of angles 5.3.3 Complementary and Supplementary angles 5.3.4 Bisector of an angle 5.4 Triangles 164 5.4.1 Parts of a triangle 5.4.2 Types of triangles 5.4.3 Important properties of triangles 5.5 Special quadrilaterals 169 5.5.1 Quadrilateral and its parts 5.5.2 Special type of quadrilaterals 6. PRACTICAL GEOMETRY 173 6.1 Geometrical instruments box 173 6.2 Line segment 176 6.3 Constructing a line segment of a given measurement 177 6.4 Measuring the length of a given line segment 178 6.5 Constructing a line perpendicular to a given line at a given point on it 179 6.6 Constructing the perpendicular bisector of a given line segment 181 6.7 Measuring angles 185 6.8 Constructing angles of given measures 188 6.8.1 Constructing 90° and 45° using paper folding method 6.8.2 Drawing angles with the help of a protractor 6.9 Constructing the angle bisector of a given angle 189 6.9.1 Paper folding method 6.9.2 Using protractor and compass 7. HANDLING DATA 191 7.1 Meaning of an average (mean) 191 7.2 Median 194 7.3 Mode 195 7.4 Pictograph 197 7.5 Bar Graph 201 ANSWERS 207 1. NUMBER WORK “Numbers are my friends” says Ramanujan, the well known Indian Mathematician. He loved numbers and his contribution to Mathematics is great. We are familiar with some fundamental mathematical calculations with numbers in the previous classes. Now we briefly revise the number system which we have studied. Any number is a concept. ‘one’ is a number name and we use the numeral or symbol ‘1’ to denote it. ‘Five’ is a number name and we use the numeral ‘5’ to denote it. In olden days, different symbols were used in different parts of the world to denote the numerals. The present system is based on ten numerals 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. It was developed by Indians. Arabs made these numerals known to western countries. Hence these numerals are called Indo-Arabic numerals. This system is universally accepted. 1.1 Numbers – Revision 1.2 Four fundamental operations on Whole numbers 1.3 Number patterns 1.4 Large numbers in Exponential form 1.5 Tests of divisibility – Revision 1.6 Greatest common divisor and Least common multiple 1.7 Integers 1.8 Fractions 1.9 Decimal numbers. 1.1 Numbers – Revision 1.1.1 Natural Numbers and Whole Numbers 1.1.2 Face value and Place value 1.1.3 Expanded form 1.1.1. (a) Natural Numbers : The counting numbers 1, 2, 3, ……… are called natural numbers. Natural numbers are beginning with 1 and increasing one by one. The set of natural numbers is denoted by the symbol N. In the set of natural numbers, 2 is called the successor of 1. 1 is called the predecessor of 2 and 3 is called successor of 2 and 2 is called predecessor of 3. Can you give the last natural number? Thus N = {1, 2, 3, ……… } (b) Whole Numbers : If we include the number 0 to the set of natural numbers, we get 0, 1, 2, 3, ……… . This is called the set of whole numbers and is denoted by the symbol W. Thus W = {0, 1, 2, 3, ……… } 1 1.1.2 Face Value and Place Value The numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are called digits. It is by using these ten digits, we are generating all the numbers in the set of whole numbers. For example, to write the numeral for two thousand four hundred and eighty seven, we write 2487. Here we use the digits together with place value. Every digit in a number has a face value and a place value. For example in 2487, the digits we have used are 2, 4, 8 and 7. The face value of these digits are respectively 2, 4, 8 and 7 only. However depending upon the place they occupy in the number, each digit has a distinct value. In 2487, the place value of 2 is 2000; the place value of 4 is 400 ; the place value of 8 is 80 ; the place value of 7 is 7 ; Using the ten digits and the concept of place value, we can write any number. The place value increases in powers of 10, starting from units. The digits in numbers from right to left have the place values of 1, 10, 100, 1000, 10000 etc. Thus the place value of each digit in 894063217 is as follows : The place value of 7 is 7 ones 7 The place value of 1 is 1 ten 10 The place value of 2 is 2 hundreds 200 The place value of 3 is 3 thousands 3000 The place value of 6 is 6 ten thousands 60000 The place value of 0 is 0 lakh 0 The place value of 4 is 4 ten lakhs 4000000 The place value of 9 is 9 crores 90000000 The place value of 8 is 8 ten crores 800000000 Now this number can be read as eightynine crore, forty lakh, sixtythree thousand two hundred and seventeen and is written as 89,40,63,217. Another method of expressing the numbers is known as international notation.
Load more

Recommended publications
  • LOK SABHA ___ SYNOPSIS of DEBATES (Proceedings Other Than
    LOK SABHA ___ SYNOPSIS OF DEBATES (Proceedings other than Questions & Answers) ______ Tuesday, July 15, 2014 / Ashadha 24, 1936 (Saka) ______ STATEMENT BY MINISTER Re: Reported meeting of an Indian journalist with Hafiz Saeed in Pakistan. THE MINISTER OF EXTERNAL AFFAIRS AND MINISTER OF OVERSEAS INDIAN AFFAIRS (SHRIMATI SUSHMA SWARAJ): On the issue which was raised yesterday in the House, I, with utmost responsibility and categorically and equivocally would like to inform this House that the Government of India has no connection to the visit by Shri Ved Prakash Vaidik to Pakistan or his meeting with Hafiz Saeed there. Neither before leaving for Pakistan nor at his arrival there, he informed the Government that he was to meet Hafiz Saeed there. This was his purely private visit and meeting. It has been alleged here that he was somebody‟s emissary, somebody‟s disciple or the Government of India had facilitated the meeting. This is totally untrue as well as unfortunate. I would like to reiterate that the Government of India has no relation to it whatsoever. *MATTERS UNDER RULE 377 (i) SHRI BHARAT SINGH laid a statement regarding need to start work on multipurpose project for development of various facilities in Ballia Parliamentary constituency, Uttar Pradesh. (ii) SHRI BHANU PRATAP SINGH VERMA laid a statement regarding need to extend Shram Shakti Express running between New Delhi to Kanpur upto Jhansi. (iii) SHRIMATI JAYSHREEBEN PATEL laid a statement regarding need to expedite development of National Highway No. 228 declared as a Dandi Heritage route. (iv) SHRI DEVJI M. PATEL laid a statement regarding need to provide better railway connectivity in Jalore Parliamentary Constituency in Rajasthan.
    [Show full text]
  • TOP 100 Expected GK Questions on Indian Railways | Specially for RRB NTPC 2019
    TOP 100 Expected GK Questions on Indian Railways | Specially for RRB NTPC 2019 1) What is the rank of Indian Railways in the world in terms a) Himsagar Express of size of the railroad network? b) Silchar Superfast Express a) 2nd c) Navyug Express b) 5th d) Vivek Express c) 4th d) 10th Answer: d) Vivek Express covers the longest train route in India. It Answer: c) originates in northern Assam and goes all the way to the Indian Railways (IR) is India's national railway system southern tip of India to Kanyakumari. It has the running time operated by the Ministry of Railways. It manages the fourth of 80 hours and 15 minutes and the distance covered is largest railway network in the world by size, with 121,407 4,233 kilometres. kilometres of total track over a 67,368-kilometre route. 5) Which express is the currently operational trans-border 2) Which is India’s first passenger train that ran between train between India and Pakistan? Bombay and Thane in 1853? a) Thar Express a) Great Indian Peninsula Railway b) Akbar Express b) Central Railway c) Samjhauta Express c) Bombay Baroda Railway d) Both a and c d) Mumbai Suburban Railway Answer: d) Answer: a) Currently, there are two trans-border trains between India The Great Indian Peninsula Railway was incorporated on 1 and Pakistan. First Is Samjhauta Express that operates on August 1849 by an act of the British Parliament. It was a Delhi-Lahore Route via Attarti-Wagah Border whereas Thar predecessor of the Central Railway, whose headquarters Express links Jodhpur and Karachi via Munabao-Khokhrapar was at the Boree Bunder in Mumbai.It was India's first border crossing.
    [Show full text]
  • Magazine Final.Cdr
    The RAIL ` 100 enthu siast Vol. 1 No. 2 December 2016 RA The Rail Enthusiats’ Society Quarterly THE IL RAIL MODELLING Kalka-Shimla Railway REPORT N G T I M E W A R P PHOTO FEATURE! Steam Loco at RIGA Paala State Monorail Tramway The Paala State Monorail Tramway (PSMT) was a unique rail system constructed by Maharaja Sir Bhupinder Singh of Paala for movement of people and goods in his state. It operated in Paala state between 1907 and 1927. PSMT was based on the Ewing system wherein rail-guided vehicles use a balancing wheel for balancing. 95% of the load is taken by the single rail and the remaining 5% by the balancing wheel. The PSMT can be seen at the Naonal Rail Museum at New Delhi where it is one of its many exhibits. Musings of the Editor... The first step toward change is awareness. The second step is acceptance. – Nathaniel Branden The Rail Enthusiast, launched on the 6th of August earlier this year, was our first step towards change – a change that envisages the recognion and appreciaon of the rail enthusiast; a change that sees more and more persons of the automove generaon A Magazine being aracted to the fascinang world of rail lovers and addicts; a change that creates of the Rail Enthusiast, by the Rail Enthusiast & awareness of the realm of the railway in the general public. It pleases us that some of for the Rail Enthusiast these changes, though embryonic, are appearing as shas of light at the end of the tunnel.
    [Show full text]
  • Booking Train Ticket Through Internet Website: Irctc.Co.In Booking
    Booking Train Ticket through internet Website: irctc.co.in Booking Guidelines: 1. The input for the proof of identity is not required now at the time of booking. 2. One of the passengers in an e-ticket should carry proof of identification during the train journey. 3. Voter ID card/ Passport/PAN Card/Driving License/Photo Identity Card Issued by Central/State Government are the valid proof of identity cards to be shown in original during train journey. 4. The input for the proof of identity in case of cancellation/partial cancellation is also not required now. 5. The passenger should also carry the Electronic Reservation Slip (ERS) during the train journey failing which a penalty of Rs. 50/- will be charged by the TTE/Conductor Guard. 6. Time table of several trains are being updated from July 2008, Please check exact train starting time from boarding station before embarking on your journey. 7. For normal I-Ticket, booking is permitted at least two clear calendar days in advance of date of journey. 8. For e-Ticket, booking can be done upto chart Preparation approximately 4 to 6 hours before departure of train. For morning trains with departure time upto 12.00 hrs charts are prepared on the previous night. 9. Opening day booking (90th day in advance, excluding the date of journey) will be available only after 8 AM, along with the counters. Advance Reservation Through Internet (www.irctc.co.in) Booking of Internet Tickets Delivery of Internet Tickets z Customers should register in the above site to book tickets and for z Delivery of Internet tickets is presently limited to the cities as per all reservations / timetable related enquiries.
    [Show full text]
  • Prepared by Prepared by FA&CAO/Traffic FA&CAO/Traffic
    Prepared by FA&CAO/Traffic SOUTHERN RAILWAY 1 CONTENTS TOPICS PAGE NO. PREFACE 3 INTRODUCTION 4 TATKAL SYSTEM 4 TABLES Train No. From To Train Name 12657 MAS SBC BANGALORE MAIL 5 12658 SBC MAS CHENNAI MAIL 6 12673 MAS CBE CHERAN EXPRESS 7 12674 CBE MAS CHERAN EXPRESS (Return) 8 16669 MAS ED YERCAUD EXPRESS 9 16670 ED MAS YERCAUD EXPRESS (Return) 10 16177 MS KMU ROCKFORT EXPRESS 11 16178 KMU MS ROCKFORT EXP. (Return) 12 12637 MS MDU PANDIAN EXPRESS 13 12638 MDU MS PANDIAN EXPRESS (Return) 14 16222 MAS MYS KAVERI EXPRESS 15 16221 MYS MAS KAVERI EXPRESS (Return) 16 12671 MAS MTP NILGIRI EXPRESS 17 12672 MTP MAS NILGIRI EXPRESS (Return) 18 12631 MS TEN NELLAI EXPRESS 19 12632 TEN MS NELLAI EXPRESS (Return) 20 12633 MS CAPE KANYAKUMARI EXPRESS 21 12634 CAPE MS KANYAKUMARI EXP. (Ret) 22 16723 MS TVC ANANTHAPURI EXPRESS 23 16041 MAS ALLP ALLEPPEY EXPRESS 25 16042 ALLP MAS ALLEPPEY EXPRESS (Return) 26 16724 TVC MS ANANTHAPURI EXP. (Ret) 27 16627 MAS MAQ WEST COAST EXPRESS 28 16628 MAQ MAS WEST COAST EXP. (Return) 30 12695 MAS TVC TRIVANDRUM EXPRESS 32 12696 TVC MAS TRIVANDRUM EXP. (Return) 33 OUTCOME OF ANALYSIS 34 SINGLE FARE SECTOR 34 TWO FARE SECTOR 35 THREE FARE SECTOR 35 FOUR FARE SECTOR 36 ADDITIONAL FARE SECTOR 36 SUMMARY OF ANALYSIS 37 INFERENCE 39 SUGGESTIONS – MAIN 39 ADVANCE RESERVATION PERIOD AND TATKAL QUOTA 39 ADDITIONAL GENERAL SUGGESTIONS 40 CONCLUSION 41 2 TRAIN BASED RESTRUCTURING OF PASSENGER FARES PREFACE: The telescopic and distance slab basis passenger fare structure is followed by the railways for a long time without adopting any major changes except for some minor adjustment in distance slabs, reservation restriction upto minimum distances for some selected trains etc.
    [Show full text]
  • 579 EARLY TRANSPORT SYSTEM in COIMBATORE S. Jayashree
    International Journal of Current Research and Modern Education (IJCRME) Impact Factor: 6.925, ISSN (Online): 2455 - 5428 (www.rdmodernresearch.com) Volume 3, Issue 1, 2018 EARLY TRANSPORT SYSTEM IN COIMBATORE S. Jayashree Ph.D Research Scholar, PG Research Department of History, Government Arts College (Autonomous), Coimbatore, Tamilnadu Cite This Article: S. Jayashree, “Early Transport System in Coimbatore”, International Journal of Current Research and Modern Education, Volume 3, Issue 1, Page Number 579-581, 2018. Copy Right: © IJCRME, 2018 (All Rights Reserved). This is an Open Access Article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Early Transport System in Coimbatore: Coimbatore also known as Kovai, is one of the major industrial cities in South India. In the early period Salem, Trichy, Erode and Coimbatore area were called as the Kongu Region and later Coimbatore became a separate city and was administered by the Coimbatore Municipality. It is the second largest city in Tamilnadu after Chennai. Coimbatore is well known for its textile, industrial, commercial, educational, information technology, healthcare and manufacturing hub of Tamilnadu. It is called by another name called the Manchester of South India for its extensive cotton industry fed by the surrounding Cotton fields. Coimbatore is located on the banks of the Noyyal river and surrounded by the Western Ghats. The transport sector is one of the core sectors of the economy, since it supports the infrastructure needs of all developments 1. In the prehistoric period man travelled on foot with loads on his back and head.
    [Show full text]
  • Names of Trains
    NAMES OF TRAINS Agniveena Express 2341/ 2342 Howrah – Asansol (ER Howrah division) In Bangla it means “The Fiery Lute”. This is the name given to the collection of poems by the celebrated Bengali poet, musician, revolutionary and philosopher, Kazi Nazrul Islam. He was born in Burdwan district in 1899 and died in Dhaka in 1976. He is the national poet of Bangladesh, and also honoured in India. Ahilyanagari Express 6325/ 6326 Indore – Thiruvananthapuram Central (SR Thiruvananthapuram division) Rajmata Ahilyadevi Holkar (1725-1795, ruled 1767-1795) also known as the Philosopher Queen was a Holkar dynasty Queen of the Malwa kingdom. She took over reigns of the kingdom after the death of her husband and father-in-law. She moved the capital to Maheshwar south of Indore on the Narmada River. She also built temples and Dharamshalas (free lodging)at sacred sites outside her kingdom, at prominent religious places like Dwarka, Kashi Vishwanath in Varanasi, Ujjain, Nasik, Parli Vaijnath and Somnath. The city of Indore is sometimes called Ahilyanagari in her memory. Ahimsa Express 1095/ 1096 Ahmadabad – Pune (CR Pune division) The name is also sometimes given to 1087/ 1088 Veraval – Pune Express, 1089/ 1090 Jodhpur – Pune Express and 1091/ 1092 Bhuj – Pune Express, as all these trains are “derived” from 1095/ 1096. Ahimsa is a Sanskrit term meaning “to do no harm” (literally, the avoidance of violence or himsa). Ahimsa was one of the main principles which Gandhiji followed in his life. Pune was the place where Gandhiji was imprisoned and where his wife passed away, and Ahmadabad was where he set up his Ashram.
    [Show full text]
  • India and Her Neighbours
    Ch in a Nepal Bhutan INDIA AND HER Myanmar Bangladesh NEIGHBOURS Sri Lanka Our Neighbours Name the South Asian regional grouping of and north west. countries of India in which India is a member. The Indian State that shares the maximum frontier (a) ASEAN (b) SAARC (c) APEC (d) D-8 with China is Arunachal Pradesh. Ans: (b) SAARC The Indian States which touch Pak border are The 8 members of South Asian Association of Jammu and Kashmir, Punjab, Rajasthan and Regional Co-operation (SAARC) are India, Gujarat in the order from north to south. Bangladesh, Pakistan, Bhutan, Nepal, Sri Lanka, PoK is Pak occupied Kashmir. Maldives and Afghanistan. Its 8th member Afganistan was admitted to SAARC in 2006. Muzaffarabad is the capital of Pok. India is the 7th largest Country and 2nd most LAC : Line of Actual Control. populous in the World. Area of Jammu and Kashmir 2,22236 Sq.km. This Westernmost State of India is Gujarat, includes 78,114 sq km under illegal occupation Northernmost State of India is Jammu & Kashmir; of Pakistan, 5180 sq.km illegally handed over by Eastern most State is Arunachal Pradesh and Pakistan to China and 37,555 sq.km under illegal Southernmost State is Tamil Nadu. occupation of China. South easternmost State of India is Mizoram The States which surround Bangladesh are West South easternmost part of India is Nicobar Island. Bengal, Assam, Meghalaya, Tripura and India is the second largest Peninsula in the World. Mizoram. The largest Peninsula is Arabia. The States which share border with Myanmar are Arunachal Pradesh, Nagaland, Manipur and Rajasthan is one of the border States of India Mizoram.
    [Show full text]
  • [IRFCA] Indian Railways
    Abita Begum Express: Delhi Jn. - Raxaul [OLD –now runs as Satyagraha Exp.] DLI d 17.15; RXL a 15.10/RXL d 09.00;DLI a 07.35. (Abita Ahmed Begum, wife of former President Fakhruddin Ali Ahmed) Agnibeena Express: Howrah - Asansol (former Bidhan Exp.) HWH d 18.20; ASN a 21.30/ASN d 05.30; HWH a 08.45. (Name of work by Bengali poet Nazrul Islam) Ahilyanagari Express: Thiruvananthapuram – Indore Jn. TVC d 05.30; INDE a 03.50/INDE d 16.40; TVC a 17.20. (Another (older) name for Indore, built by Holkar queen Ahilyabai) Ahimsa Express: Ahmedabad - Pune . ADI d 16.00; PUNE a 03.50/PUNE d 19.45; ADI a 07.35. (Ahimsa = non-violence, associated with Gandhi) Air-Conditioned Express (AC Express) : Name used for several trains in the past when air-conditioning was rare. Howrah - New Delhi [OLD-now Rajdhani/Duronto Exp], Mumbai Central - New Delhi [OLD-now Rajdhani/Duronto Exp.], Chennai Central - New Delhi [OLD-now Rajdhani/Duronto Exp.], Mumbai CST - Howrah [OLD- now Duronto Exp.], Mumbai CST - Madras Central [OLD- now Duronto Exp(proposed)], Chennai Central - Howrah [OLD- now Duronto Exp(proposed)]. Ajanta Express: Secunderabad – Manmad. SC d 18.10; MMR a 06.30/MMR d 21.00; SC a 09.10 (Ajanta caves near Aurangabad) Akal Takht Express: Sealdah – Amritsar. SDAH d 07.40; ASR a 16.55/ASR d 06.05; SDAH a 15.20; (Sikh holy site at the Golden Temple in Amritsar) Ala Hazrat Express: Bhuj - Bareilly City. BHUJ d 12.50/15.20; BEC a 20.15\BEC d 06.00; BHUJ a 13.20/11.15.
    [Show full text]
  • English Reader
    ENGLISH READER HIGHER SECONDARY - FIRST YEAR PART II - ENGLISH Untouchability is a sin Untouchability is a crime Untouchability is inhuman TAMILNADU TEXTBOOK CORPORATION College Road, Chennai – 600 006. © Government of Tamilnadu First Edition - 2004 Reprient - 2006 Chairperson Dr. S. SWAMINATHA PILLAI Former Director School of Distance Education Bharathiar University, Coimbatore Overall Reviewer Thiru S.GOMATHINATHAN Special Officer, ELT / Reader, D.T.E.R.T. (Retired), W – 5 (Old 302), 19th Street, Annanagar Western Extension, Chennai - 600 101. Reviewers : Dr. V. Saraswathi Dr. Noor Jehan Kother Adam Former Professor of English Reader in English University of Madras, Chennai. Ethiraj College for Women, Chennai. Authors : Ms. Priscilla Josephine Sarah S. Researcher in ELT W-5 (Old 302), 19th Street, Anna Nagar Western Extension, Chennai. Dr. A. Joseph Dorairaj Thiru. S. Muthukrishnan Reader in English Principal Gandhigram Rural University Jaigopal Garodia Vivekananda Vidyalaya Gandhigram Matriculation Higher Secondary School Dindugul District. Annanagar, Chennai. Ms. Nirmala Jairaj Thiru. K.V. Renganathan Language Consultant Former Principal 5/36, 13th Avenue, Harrington Rd. Govt. Muslim Teachers’Training Institute Chetpet, Chennai. Triplicane, Chennai. Price : Rs. 18.00 This book has been prepared by The Directorate of School Education on behalf of the Government of Tamilnadu. This book has been printed on 60 G.S.M. paper. Printed by Offset at : SENTHIL OFFSET PERINTERS, SIVAKASI - 626 123. THE NATIONAL ANTHEM FULL VERSION Jana-gana-mana-adhinayaka jaya he Bharata-bhagya-vidhata. Punjaba-Sindhu-Gujarata-Maratha- Dravida-Utkala-Banga Vindhya-Himachala-Yamuna-Ganga Uchchhala-jaladhi-taranga Tava Subha name jage, Tava Subha asisa mage, Gahe tava jaya-gatha. Jana-gana-mangala-dayaka jaya he Bharata-bhagya-vidhata.
    [Show full text]
  • Lok Sabha Debate
    14.11 hrs. *DEMAND FOR SUPPLEMENTARY GRANTS (RAILWAYS), 2005-06 AND *DEMANDS FOR EXCESS GRANTS (RAILWAYS), 2002-03 MR. DEPUTY SPEAKER: Now, we will take up Item Numbers 13 and 14 together relating to Demand for Supplementary Grant (Railways) and Demands for Excess Grants (Railways). Motions moved: "That the supplementary sums not exceeding the amounts shown in the third column of the Order Paper be granted to the President of India, out of the Consolidated Fund of India, to defray the charges that will come in course of payment during the year ending the 31st day of March, 2006, in respect of the head of Demand entered in the second column thereof against Demand No.16." "That the respective excess sums not exceeding the amounts shown in the third column of the Order Paper be granted to the President of India, out of the Consolidated Fund of India, to make good the excess on the respective grants during the year ended the 31st day of March, 2003, in respect of the heads of demands entered in the second column thereof against Demand Nos. 14, 15 and 16." Shri Lakshman Singh to speak. *Moved with the recommendation of the President. ( ) : , ग , स ग औ स ग औ ए ए , स ए 383.64 औ स 425 स औ स ए ग , सस 320 स स ए स स ए स स स ग ए स 320 स , इस ग औ स - ए ग औ इ इ ए - सफ ग स , स ए स ग स एग , स स ग स , स ए औ ग , स ए .( ) , ए औ स स , स ए फ इ ग 1988 ग स फ इ ग औ स औ औ औ स ए ग स ए ए, स ग औ स स इ स ग , स ग 5283 इ , 5497 इ औ 4850 इ औ इ इ स ए औ स स ए स ए ए , सस स स स स ए स स ए ए स स औ इस ए स ए , स ए स , इस ए इस ओ इ औ स स स औ स इस ग स एग , ओ ग , 2 इ , ग 13 इ औ
    [Show full text]
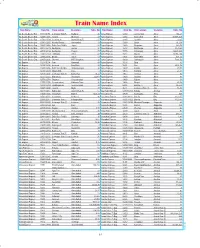
  • Train Name Index Train Name Train No
    Train Name Index Train Name Train No. From station To station Table No. Train Name Train No. From station To station Table No. AC Double Decker Exp 11085/11086 Lokmanya Tilak(T) Madgoan 26 Ajmer Express 12414 Jammu Tawi Ajmer 16A,23 AC Double Decker Exp. 12385/12386 Howrah Dhanbad 37 Ajmer Express 12720 Hyderabad Ajmer 9A,53A,54A AC Double Decker Exp. 12583/12584 Lucknow Jn. Anand Vihar (T) 25 Ajmer Express 12987 Sealdah Ajmer 23,65 AC Double Decker Exp. 12931/12932 Mumbai Central Ahmedabad 11 Ajmer Express 12989 Dadar Ajmer 11,23A AC Double Decker Exp. 12985/12986 Delhi Sarai Rohilla Jaipur 23 Ajmer Express 13423 Bhagalpur Ajmer 24A,72 AC Double Decker Exp. 22117/ 22118 Kachiguda Guntur 30 Ajmer Express 15237 Darbhanga Ajmer 13,79,64 AC Double Decker Exp. 22119/ 22120 Kachiguda Tirupati 71 Ajmer Express 15715 Kishanganj Ajmer 18A,23,25A AC Double Decker Exp. 22183/22184 Habibganj Indore 43 Ajmer Express 16210 Mysuru Ajmer 11,19A,23A AC Double Decker Exp. 22185/22186 Bhopal Indore 43 Ajmer Express 17020 Hyderabad Ajmer 9,54,53 AC Double Decker Exp. 22625/22626 Chennai KSR Bengaluru 20 Ajmer Express 18009 Santragachi Ajmer 73,41,72 AC Express 11213/11214 Pune Amravati 44 Ajmer Express 18207 Durg Ajmer 72 AC Express 12429/12430 Lucknow New Delhi 25 Ajmer Express 18421 Puri Ajmer 23,34,78 AC Express 12455/12456 Delhi Sarai Rohilla Sri Ganganagar 39 Ajmer Express 19607 Kolkata Ajmer 73,72 AC Express 12493/12494 Nizamuddin Pune 4 Ajmer Express 19610 Haridwar Ajmer 23,84 AC Express 12519/12520 Lokmanya Tilak (T) Kamakhya 18,24 Ajmer Express
    [Show full text]