DOCSLIB.ORG

Clustering in Light Nuclei with Configuration Interaction Approaches Konstantinos Kravvaris

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Clustering in Light Nuclei with Configuration Interaction Approaches Konstantinos Kravvaris Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2018 Clustering in Light Nuclei with Configuration Interaction Approaches Konstantinos Kravvaris Follow this and additional works at the DigiNole: FSU's Digital Repository. For more information, please contact [email protected] FLORIDA STATE UNIVERSITY COLLEGE OF ARTS AND SCIENCES CLUSTERING IN LIGHT NUCLEI WITH CONFIGURATION INTERACTION APPROACHES By KONSTANTINOS KRAVVARIS A Dissertation submitted to the Department of Physics in partial fulfillment of the requirements for the degree of Doctor of Philosophy 2018 Konstantinos Kravvaris defended this dissertation on May 11, 2018. The members of the supervisory committee were: Alexander Volya Professor Directing Dissertation David Kopriva University Representative Ingo Weidenhoever Committee Member Simon Capstick Committee Member Laura Reina Committee Member The Graduate School has verified and approved the above-named committee members, and certifies that the dissertation has been approved in accordance with university requirements. ii ACKNOWLEDGMENTS This thesis would not have been possible without the constant encouragement of Professor Alexan- der Volya. His patience was a critical ingredient throughout the research and writing process. It was always a pleasure discussing research, administrative and general topics. I am also grateful for the committee members' guidance when necessary. I would also like to thank Professor Jorge Piekarewicz for being a great teacher and exposing me to more problems in nuclear physics. Finally, special thanks goes to Professor Efstratios Manousakis for all his help before and during my PhD studies. I would also like to thank everyone who made the non-research part of my studies enjoyable and interesting, Maria Anastasiou, Konstantinos Kountouriotis, Katerina Chatziioannou, David Fernandez, Hailey Nicol (soon to be Fernandez), and Daniel Lanford. Finally, for navigating the bureaucratic maze, I would like to thank Jonathan Henry, Brian Wilcoxon and Felicia Youngblood. iii TABLE OF CONTENTS List of Tables . vi List of Figures . viii List of Symbols . ix List of Abbreviations . .x Abstract . xi 1 Introduction 1 2 Methods 5 2.1 Harmonic Oscillator . .5 2.1.1 Coordinate Transformations . .6 2.2 Configuration Interaction Approach in a HO Basis . .9 2.2.1 HO Basis Expansion . .9 2.3 Traditional Shell Model . 11 2.4 No Core Shell Model . 12 2.5 Resonating Group Method . 12 2.6 Spectroscopic Factors . 15 2.6.1 Traditional Spectroscopic Factors . 16 2.6.2 Normalized Spectroscopic Factors . 16 2.6.3 Dynamic Spectroscopic Factors . 17 2.7 Coupling to Continuum . 18 2.8 Rotational Bands . 20 2.8.1 Elliott's SU(3) Model for Rotations . 22 3 Constructing Cluster Channels 23 3.1 Antisymmetry . 23 3.2 The Gloeckner-Lawson Procedure . 24 3.3 SU(3) Method . 25 3.4 Center of Mass Boosting Method . 27 3.5 Constructing the Channels . 29 4 Traditional Shell Model Studies 33 4.1 α Particle Wave Function . 33 4.2 Clustering in the sd Shell . 34 4.2.1 The Case of 20Ne.................................. 37 4.2.2 Evolution of Clustering with Increasing Nucleons . 39 4.3 Superradiance in 13C and α Clustering . 41 iv 5 No Core Shell Model Studies 43 5.1 The Nucleus 8Be ...................................... 43 5.2 The Nucleus 9Be ...................................... 46 5.3 The Nucleus 10Be...................................... 48 5.4 The 3α System . 50 6 Conclusions 52 Appendix A Second Quantization 54 B CM Boosting Operator Normalization Coefficients 56 C Calculation of Radial Integrals with HO Wave Functions 59 D CM Boost and Recoupling Examples 61 E Hamiltonian Kernels for the 2α System 65 F Tables of Spectroscopic Amplitudes 67 Bibliography . 82 Biographical Sketch . 94 v LIST OF TABLES 3.1 Select configuration content of NCSM wave functions for 4He with ¯h! = 20 MeV boosted to a CM boosted state with n = 4 and ` =0. .................. 29 3.2 Moshinsky coefficients for different mass ratios d = AD=Aα coupling to a final HO wave function with CM quantum numbers N = L = 0 and relative quantum numbers n = 2; ` =0. ......................................... 31 4.1 Transition rates and α spectroscopic factors for the 20Ne rotational band members with the USDB interaction. 37 4.2 Comparison between new and experimental SF for low-lying states in 21Ne. 40 4.3 Energies, widths in MeV and α spectroscopic factors (structural) for the two lowest 3=2+ states in 13C...................................... 42 5.1 Alpha decay widths and spectroscopic factors for the first 3 states in 8Be using different oscillator parameters ¯h!. The S(dyn) are calculated with the lowest energy solution of 8 the RGM in each case projecting on the Nmax = 4 corresponding Be wave function. Widths are calculated with a fixed channel radius of R = 3:6 fm . 45 5.2 Contributions to the Hamiltonian from different interaction components in MeV. Then numbers in parentheses indicate number of nodes n and angular momentum ` in the relative coordinate of the 2α channel. V0;1 correspond to the different jTzj values for the interaction. The second column refers to contribution to a single α particle. We use the JISP16 interaction with ¯h! = 25 MeV. 46 5.3 Negative parity band energies and SF for 9Be. The numbers in parentheses denote the number of available quanta in the relative motion between the 2 clusters. The SF are calculated with ¯h! = 20 MeV. The sixth column marked with a single star refers to dynamic SF calculated with additional channels built on the 5He(1/2−) state. The final column marked with two stars refers to a calculation with channels restricted to having an 8Be +n form. 48 5.4 Dynamic SF for rotational band members in 10Be. The last columns labeled with a (*) refers to calculations with channels constructed with the excited 2+ state of 6He. The states belonging to the two different rotational bands are separated by a line. The SF is evaluated with the dominant channel(s). 48 5.5 Leading SU(3) irreducible representation components and particle-hole content of states recognized as belonging to rotational bands in 10Be. The ordering is the same asin5.4............................................ 50 vi 5.6 Ground state binding energy and excitation energies for rotational band members of 12C using the NCSM and RGM with ¯h! = 20 MeV. 51 D.1 Index ordering (k) of single particle orbitals. The ± superscirpt refers to the m = ±1=2 projection of each orbital. 62 D.2 Index ordering (k) of neutron single particle orbitals for the sp space. The proton indexing follows the same order but offset by 8. 63 vii LIST OF FIGURES 1.1 Ikeda diagram showing the location of different modes of clusterization and the re- spective decay thresholds. .3 2.1 Broad alpha clustering states in light nuclei. The data for 10Be are taken from [88] and for 18O from [89] . 19 3.1 A schematic depiction of the process of transfering the quanta of motion from the CM of an α cluster to the relative motion between the α and a daughter nucleus. The primes indicate the (invariant) internal wave functions of both nuclei. 30 4.1 Ab initio calculations for the ground state energy (left) and the s4 component of 4 the He wave function (right) with the JISP16 interaction spanning multiple Nmax truncations and ¯h! values. 34 4.2 Old (dashed) and New (solid) spectroscopic factors comparison with experimental data from [115, 25] using the USDB [61] interaction. Red (blue) poinst correspond to α knockout (pickup). The dotted line corresponds to a calculation with a realistic α wave function, obtained using the NCSM withh! ¯ = 14 MeV and Nmax = 8. 35 4.3 Comparison between (new) α SF calculated with different wave functions for the α particle. For the Nmax = 0; 4; 8 there are 1; 3; 5 channels open respectively. 36 4.4 (a) Experimental population of states in 20Ne from (6Li,d) and (b) theoretical pre- dictions for SF in a (0+1)ph calculation of 20Ne. To match the experimental figure, energy is increasing to the left. Details of the calculation are given in main text. Figure (a) is reproduced with permission from [123]. 38 4.5 Low-lying RGM, full USDB and experimental spectra of 21Ne. 40 5.1 Low-lying spectra of 8Be calculated with the JISP16 interaction at varioush! ¯ values in units of MeV. 44 5.2 RGM calculations of the rotational band of 8Be for ¯h! = 20 MeV with the JISP16 interaction and with the α particle wave function taken from a NCSM calculation with the corresponding value of Nmax. The value N in the plot reflects the total number of HO quanta available to the relative motion between the two clusters. 47 5.3 Cluster rotational bands in 9Be. N refers to the total number of quanta available in the relative motion; even (odd) N corresponds to negative (positive) parity bands. Top (bottom) plot corresponds to positive (negative) parity states. 49 viii LIST OF SYMBOLS π 3:1415926 ::: ¯hc 197:327 ::: MeV fm n The number of nodes of in the radial coordinate, n = 0; 1; 2 ::: l The orbital angular momentum of a single particle orbital. m The z - axis projection of the angular momentum. ` The relative orbital angular momentum of two clusters. N The total number of oscillator quanta, N = 2n + l. Nmax Number of allowed excitation quanta in No Core Shell Model. s; p; d; f : : : Spectroscopic notation for orbitals with l = 0; 1; 2; 3 ::: α Ln(x) Generalized Laguerre polynomial. Ylm(θ; φ) Usual Spherical Harmonic. JM Cj1m1j2m2 Clebsch Gordan Coefficient coupling j1m1 and j2m2 to JM [41]. Mn`NL Moshinsky Coefficient for a transformation with angle ' [45] ' n1l1n2l2 Mn`NL n1l1n2l2 Coefficient for a transformation to the CM of equal mass particles (' = π=4) ix LIST OF ABBREVIATIONS HO Harmonic Oscillator CI Configuration Interaction SM Traditional Interacting Shell Model NCSM No Core Shell Model RGM Resonating Group Method CSM Continuum Shell Model Harmonic Oscillator Representation HORSE of Scattering Equations SF Spectroscopic Factor NN Nucleon-Nucleon JISP J-Inverse Scattering Potential x ABSTRACT The formation of sub-structures within an atomic nucleus, appropriately termed nuclear clustering, is one of the core problems of nuclear many-body physics.
Load more

Recommended publications
  • Advances in Nuclear Physics
    ADVANCES IN NUCLEAR PHYSICS VOLUME 27 CONTRIBUTORS TO THIS VOLUME Stefan Scherer Igal Talmi Institut für Kernphysik The Weizmann Institute of Science Johannes Gutenberg-Universität Mainz Rehovot, Israel Mainz, Germany A Continuation Order Plan is available for this series. A continuation order will bring delivery of each new volume immediately upon publication. Volumes are billed only upon actual shipment. For further information please contact the publisher. ADVANCES IN NUCLEAR PHYSICS Edited by J. W. Negele Center for Theoretical Physics Massachusetts Institute of Technology Cambridge, Massachusetts E. W. Vogt Department of Physics University of British Columbia Vancouver, B.C., Canada VOLUME 27 KLUWER ACADEMIC PUBLISHERS NEW YORK, BOSTON, DORDRECHT, LONDON, MOSCOW eBook ISBN: 0-306-47916-8 Print ISBN: 0-306-47708-4 ©2002 Kluwer Academic Publishers New York, Boston, Dordrecht, London, Moscow Print ©2003 Kluwer Academic/Plenum Publishers New York All rights reserved No part of this eBook may be reproduced or transmitted in any form or by any means, electronic, mechanical, recording, or otherwise, without written consent from the Publisher Created in the United States of America Visit Kluwer Online at: http://kluweronline.com and Kluwer's eBookstore at: http://ebooks.kluweronline.com ARTICLES PUBLISHED IN EARLIER VOLUMES Volume 1 The Reorientation Effect • J. de Boer and J. Eicher The Nuclear Model • M. Harvey The Hartree-Fock Theory of Deformed Light Nuclei • G. Ripka The Statistical Theory of Nuclear Reactions • E. Vogt Three-Particle Scattering—A Review of Recent Work on the Nonrelativistic Theory • I. Duck Volume 2 The Giant Dipole Resonance • B. M. Spicer Polarization Phenomena in Nuclear Reactions • C.
    [Show full text]
  • APS Announces Spring 2000 Prize and Award Recipients
    Spring 2000 APS AnnouncesPrizes Spring 2000and Prize andAwards Award Recipients wenty-nine APS prizes and awards collaborates with many biologists, espe- was a postdoctoral fel- 2000 DAVISSON-GERMER PRIZE will be presented during special cially his wife of 30 years, Helen, a low at Cambridge T IN ATOMIC OR SURFACE biochemist. His group now has prototypes University (England) sessions at three spring meetings of the PHYSICS Society: the 2000 March Meeting, for a new generation of AFMs that can use in 1959-60, joined the cantilevers on order of magnitude smaller technical staff of the March 20-24, in Minneapolis, MN; the William Happer than used in current commercial AFMs. Bell Telephone Labora- 2000 April Meeting, April 29 - May 2, Princeton University tories in 1960, and the in Long Beach, CA; and the spring Citation: “For his research leading to fun- physics faculty at Ber- meeting of the APS Division of 2000 OLIVER E. BUCKLEY PRIZE keley in 1966. He has been a visiting Atomic, Molecular and Optical Phys- damental understanding and applications of atomic processes on spin or excitation scientist at Cambridge University, the Max ics, June 14 - 17, in Storrs, CT. Citations Gerald J. Dolan transfer through atomic collisions.” Planck Institutes for Solid State Physics at and biographical information for each Private Consultant Stuttgart and Radio Astronomy at Bonn, recipient follow. Additional biographi- Happer received his the Ecole Normale Superieure in Paris, the cal information and appropriate Web Theodore A. Fulton PhD degree in physics Paris Observatory, and the University of links can be found at the APS Web site Lucent Technologies from Princeton Uni- Rome.
    [Show full text]
  • Parquet Theory in Nuclear Structure Calculations
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NORA - Norwegian Open Research Archives Parquet theory in nuclear structure calculations Elise Bergli Thesis submitted to the degree of Philosophiae Doctor Department of Physics University of Oslo February 2010 © Elise Bergli, 2010 Series of dissertations submitted to the Faculty of Mathematics and Natural Sciences, University of Oslo No. 926 ISSN 1501-7710 All rights reserved. No part of this publication may be reproduced or transmitted, in any form or by any means, without permission. Cover: Inger Sandved Anfinsen. Printed in Norway: AiT e-dit AS. Produced in co-operation with Unipub. The thesis is produced by Unipub merely in connection with the thesis defence. Kindly direct all inquiries regarding the thesis to the copyright holder or the unit which grants the doctorate. Acknowledgements This thesis is primarily, of course, my own work. It has taken quite some time, not all of it pleasant, and I look forward to finally be doing something else. However, looking back, there are several people whom I would like to thank. Without them, I would not have been able to finish. First of all, I thank my adviser Morten Hjorth-Jensen. You have pro- vided more advise and encouragement than most advisers, being accessible and ready to answer questions at almost all times, regardless of time or place. I have really learned a lot from you these years. And I would also like to thank my co-adviser Eivind Osnes for pleasant discussions and having such an immense amount of literature available.
    [Show full text]
  • Nuclear and Nuclear Excitation Energies
    ANTIBES (France ) 20 - 25 JUNE, 1994 NUCLEAR AND NUCLEAR EXCITATION ENERGIES ' ~ 9£»г* Sponsored by : CNRS/IN2P3 cl Laboratoires CEA/DAM - CEA/DSM IUR1SYS MESURES Résumés des contributions Abstracts of contributed papers ;.%•• I tpîi^ I •3' ï^^rrfV-- ^^?sji;>4.ô <,!!•*• ANTIBES, France June 20-25,1994 NUCLEAR SHAPES AND NUCLEAR STRUCTURE AT LOW EXCITATION ENERGIES Abstracts of contributed papers Résumés des contributions Edited by F. DYKSTRA, D. GOUTTE, J. SAUVAGE and M. VERGNES Institut de Physique Nucléaire F-91406 ORSAY Cedex France This volume has been prepared by Miss C. Vogelaer Ce fascicule a été préparé par Mette C. Vogelaer International Committee Comité International M. ARNOULD (Bruxelles) J. AYSTO (Jyvâskylà) J. BAUCHE (Orsay) D. BES (Buenos Aires) P. BONCHE (Saclay) H. BORNER (Grenoble) R.F. CASTEN (Brookhaven) H. DOUBRE (Orsay) D. HABS (Heidelberg) I. HAMAMOTO (Lwid; K. HEYDE (Gent) R.V.F. JANSSENS (Argonne) B. JONSON (Gôteborg) W. NAZAREWICZ (ORNL/Warsaw) E.W. OTTEN (Mamzj P. RING (Garching) H. SERGOLLE (Огаг^ P. Von BRENTANO (Ко/и) M. WEISS (Livermore) Organizing Committee Comité d'Organisation G. BARREAU (Bordeaux) J.-F. BERGER (Bruyères-le-Châtel) A. GIZON (Grenoble) D. GOUTTE (Saclay) P.H. HEENEN (Bruxelles) J. LIBERT (Orsay) M. MEYER 6Ly0rt) J. PINARD (Orsay) P. QUENTIN (Bordeaux) B. ROUSSIERE (Orjoy) J. SAUVAGE (Orsay) N. SCHULZ (Strasbourg) M. VERGNES Conférence Secrétariat Secrétariat de la Conférence F. DYKSTRA (Orsay) 232 CONTENTS - On the existence of intrinsic reflection asymmetry in Z~62, N~90 region 1 A.V. Afanasjev. S. Mizutori, I. Ragnarsson - Symmetry breaking in simple one and two level models 2 P.
    [Show full text]
  • Utilisation D'une Interaction Nucléon-Nucléon De Portée Finie
    Utilisation d’une interaction nucléon-nucléon de portée finie dans le formalisme du modèle en couches avec couplage aux états du continuum. Jean Baptiste Faes To cite this version: Jean Baptiste Faes. Utilisation d’une interaction nucléon-nucléon de portée finie dans le formalisme du modèle en couches avec couplage aux états du continuum.. Physique Nucléaire Théorique [nucl-th]. Université de Caen, 2007. Français. tel-00371317 HAL Id: tel-00371317 https://tel.archives-ouvertes.fr/tel-00371317 Submitted on 27 Mar 2009 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. GANIL T 07 01 UNIVERSITE de CAEN/ BASSE NORMANDIE U.F.R. de Sciences ECOLE DOCTORALE SIMEM THESE Présentée par Mr Jean-Baptiste FAES et soutenue le 13 avril 2007 en vue de l’obtention du DOCTORAT de l’UNIVERSITÉ de CAEN Spécialité : Constituants élémentaires (Arrêté du 07 Août 2006) Titre : Utilisation d’une interaction nucléon-nucléon de portée finie dans le formalisme du modèle en couches avec couplage aux états du continuum. MEMBRES du JURY : Mr Morten HJORTH-JENSEN, Professeur, Université de Oslo (rapporteur) Mr Van Giai NGUYEN, Directeur de recherche CNRS, IPN Orsay (rapporteur) Mr Chris HEYDE, Professeur, Université de Gent Mr Oscar NAVILIAT-CUNCIC, Professeur, Université de Caen Mme Ingrid ROTTER, Professeur, Institut für Komplexe Systeme, Dresden Mr Jan VAAGEN, Profeseur, Université de Bergen Mr Marek PLOSZAJCZAK, Directeur de recherche, GANIL Caen (Directeur de thèse) UNIVERSITE´ de CAEN/BASSE-NORMANDIE U.F.R Sciences.
    [Show full text]
  • List of EXON-2004 Participants Registered by 11 June Name
    List of EXON-2004 Participants registered by 11 June Name Title of talk Country 1. Farid Abdullin New Data on Average Charge Values of Heavy Nuclei JINR 2. Yasuhisa Abe Theoretical predictions of excitation functions for Japan synthesis of the superheavy elements 3. Nicolas Alamanos Sub Barrier Fusion with Weakly Bound Nuclei France 4. Remy Anne Technical status of SPIRAL 2 France 5. Yoshihiro Aritomo Fusion-fission dynamics for synthesis of super heavy JINR elements 6. Nasima Allial Proton-neutron pairing Algeria 7. Anatoly Artukh On the Formation Mechanism of Forward-Angle JINR Products In The Reactions 18O(35 Mev/U) + 181Ta (9Be) 8. Marcos Alvarez A global optical potential to study exotic and weakly France bound nuclei interactions. 9. Alberto Andrighetto Isotopes production from UCx target with proton Beam Italy 10. Georges Audi The 2003 Nubase Evaluation and the 2003 Atomic Mass France Evaluation 11. Olivier Bajeat Optimization of ISOL UCx targets for fission induced by France fast neutrons or electrons. Application for the Spiral 2 project and for the Alto project 12. Anatoly Barzakh Changes in the mean square charge radii of neutron Russia deficient europium isotopes measured by the laser ion source resonance ionization spectroscopy 13. Jon Batchelder Fine Structure Studies of Proton Emitters at HRIBF USA 14. Bertram Blank 2p Radioactivity France 15. Zdzislaw Blaszczak Prospects of laser spectroscopy in the study of nuclear Poland matter 16. Alexey Bogachev Yields of correlated fragment pairs in the reaction JINR 208Pb(18O,f), obtained in gamma-gamma coincidence method. 17. Virginie Bouchat Search for tetraneutrons in the breakup of 8He Belgium 18.
    [Show full text]
  • On Single Nucleon Wave Func&Ons
    On single nucleon wave funcons Igal Talmi The Weizman Instute of Science Rehovot, Israel The main success of the nuclear shell model • Nuclei with “magic numbers” of protons and neutrons exhibit extra stability. • In the shell model these are interpreted as the numbers of protons and neutrons in closed shells, where nucleons are moving independently in closely lying orbits in a common central potential well. • In 1949, Maria G.Mayer and independently Haxel, Jensen and Suess introduced a strong spin-orbit interaction. This gave rise to the observed magic numbers 28, 50, 82 and 126 as well as to 8 and 20 which were well understood. The need of an effective interaction in the shell model • In the Mayer-Jensen shell model, wave functions of magic nuclei are well determined. So are states with one valence nucleon or hole. • States with several valence nucleons are degenerate in the single nucleon Hamiltonian. Mutual interactions remove degeneracies and determine wave functions and energies of states. • In the early days, the rather mild potentials used for the interaction between free nucleons, were used in shell model calculations. The results were only qualitative at best. Theoretical derivation of the effective interaction A litle later, the bare interaction turned out to be too singular for use with shell model wave functions. It should be renormalized to obtain the effective interaction. More than 50 years ago, Brueckner introduced the G-matrix and was followed by many authors who refined the nuclear many-body theory for application to finite nuclei. • Starting from the shell model the aim is to calculate from the bare interaction the effective interaction between valence nucleons.
    [Show full text]
  • Shell Model Calculations (With Nushellx@MSU)
    Shell Model Calculations (with NuShellX@MSU) TALENT Course 6 Theory for exploring nuclear reaction experiments GANIL 1st-19th July Ed Simpson University of Surrey [email protected] Session outline • A brief theoretical overview of the shell model – References – Central potential and residual interactions – General calculation procedure • Examples of calculations – Levels and overlaps, what output is given • A practical guide to shell model calculations – Interactions, models spaces – Truncations – Pitfalls… • Overview of NuShellX@MSU calculations – Levels and overlaps Tutorial • Introduction and setup • Proton spectroscopic factors: 26Ne(-1p) [or 26Ne(d,3He)25F] A brief overview of the shell model Central potentials and residual interactions References 1. H. Grawe, Shell Model from a Practioner’s Point of View, Euroschool Lectures Vol. 1 2. T. Otsuka, Shell Structure of Exotic Nuclei, Euroschool Lectures Vol. 2 3. J. B. McGrory and B. H. Wildenthal, Ann. Rev. Nucl. Part. Sci. 30, 383 (1980) 4. B. A. Brown, Lecture Notes in Nuclear Structure Physics (2010) 5. Amos de-Shalit and Igal Talmi, Nuclear Shell Theory 6. M. Vallieres and H. Wu, in Computational Nuclear Physics I: Nuclear Structure 7. E. Caurier and F. Nowacki, Act. Phys. Pol. B 30, 705 (1999) Mean potential from NN interactions r r Mean potential felt by nucleons -50 MeV -50 MeV Short-range force of nucleons Nucleon In a Nu(t)shell • Shell-model Hamiltonian written as: 2 A p A H T V i V ( r , r ) ik 1 2 i 1 2 m i k 1 • Three-body interaction small enough at energies of interest such that effects are absorbed into effective two-body interaction A 2 A A p H T V i U ( r ) V ( r , r ) U ( r ) i ik 1 2 i i 1 2 m i k 1 i 1 H H 0 H 12 • Absorb most of the effects of the two-body interactions into a one-body central potential The shell model • We wish to solve find the eigenstates and eigenvalues (energies) of the Hamiltonian H H E • Solutions of the central part H0 are products of single particle wave functions H 0 E 1 2 3 ..
    [Show full text]
  • Nucl-Th/0511024
    Seniority conservation and seniority violation in the g9/2 shell A. Escuderos and L. Zamick Department of Physics and Astronomy, Rutgers University, Piscataway, New Jersey 08854 (Dated: July 9, 2018) Abstract The g9/2 shell of identical particles is the first one for which one can have seniority-mixing effects. We consider three interactions: a delta interaction that conserves seniority, a quadrupole– quadrupole (Q·Q) interaction that does not, and a third one consisting of two-body matrix elements taken from experiment (98Cd) that also leads to some seniority mixing. We deal with proton holes relative to a Z = 50,N = 50 core. One surprising result is that, for a four-particle system with total angular momentum I = 4, there is one state with seniority v = 4 that is an eigenstate of any two-body interaction—seniority conserving or not. The other two states are mixtures of v = 2 and v = 4 for the seniority-mixing interactions. The same thing holds true for I = 6. Another point of interest is that, in the single-j-shell approximation, the splittings ∆E = E(Imax) − E(Imin) are the same for three and five particles with a seniority conserving interaction (a well known result), but are equal and opposite for a Q · Q interaction. We also fit the spectra with a combination of the delta and Q · Q interactions. The Z = 40,N = 40 core plus g9/2 neutrons (Zr isotopes) is also considered, although it is recognized that the core is deformed. arXiv:nucl-th/0511024v3 1 Dec 2005 PACS numbers: 1 I.
    [Show full text]
  • Members of the Division of Nuclear Physics, APS FROM: Benjamin F
    TO: Members of the Division of Nuclear Physics, APS FROM: Benjamin F. Gibson, LANL – Secretary-Treasurer, DNP ACCOMPANYING THIS NEWSLETTER: Charles Glashausser, Rutgers, Vice Chair (2000) • APS Spring Meeting DNP Symposia Walter F. Henning, ANL, Past Chair (2000) • DNP Fall Meeting Speaker Nomination Form Benjamin F. Gibson, LANL, Secretary-Treasurer (2000) J. Dirk Walecka, College of William & Mary Divisional Councilor (December 2001) Christopher R. Gould, N. Carolina State Univ. (2000) Barry R. Holstein, U Mass (2001) Brian Serot, Indiana U (2000) T. James M. Symons, LBNL (2000) Robert E. Tribble, Texas A&M (2001) Future Deadlines Michael C. T. Wiescher, Notre Dame (2001) • 1 April 2000 — APS Fellowship Nominations • 4 May 2000 — Speaker Nominations for Fall Meeting 2. CALL FOR DNP COMMITTEE SUGGESTIONS • 1 July 2000 — Nominations for Bonner Prize • 1 July 2000 — Nominations for Bethe Prize The terms of some of the members of the following DNP committees • 1 July 2000 — Nominations for Dissertation Award expire in April 2000: Bethe, Bonner, Fellowship, Nominating, Home Page, and Education. Suggestions from the DNP membership for new members of these committees for 2000 are welcome and should be sent WWW Home Page for DNP - “http://www.phy.anl.gov/dnp/”. to Hamish Robertson. A list of committee members for 2000 will be published in the August newsletter. A worldwide web home page for the Division of Nuclear Physics is currently available at “http://www.phy.anl.gov/dnp/”. Information of interest to DNP members, such as current NP topics, deadlines for Inside . meetings, prizes, nomination forms, special announcements, and useful links are listed there.
    [Show full text]
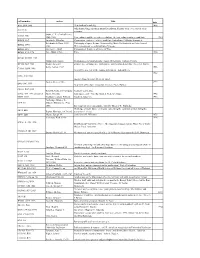
  • Call Number Author Title Date AG5 .B64 2006 New Book of Knowledge
    call number author Title date AG5 .B64 2006 New book of knowledge. 2006 John Simon Guggenheim memorial foundation. Reports of the secretary & of the AS911.J6 treasurer. Snow, C. P. (Charles Percy), AZ361 .S56 1905-1980 Two cultures and the scientific revolution, the two cultures and a second look 1963 BD632 .F67 Formánek, Miloslav. Časoprostor v politice : některé problémy fyzikalismu / Miloslav Formánek. Reichenbach, Hans, 1891- Philosophy of space & time. Translated by Maria Reichenbach and John Freund. BD632 .R413 1953. With introductory remarks by Rudolf Carnap. BD632.G92 Gurnbaum, Adolf Philosophical Problems of Space of Time BD638 .P73 1996 Price, Huw, 1953- Price. 1996 BH301.N3 H55 1985 Hildebrandt, Stefan. Mathematics and optimal form / Stefan Hildebrandt, Anthony Tromba. BT130 .B69 1983 Brams, Steven J. omniscience, omnipotence, immortality, and incomprehensibility / Steven J. Brams. Berry, Adrian, 1937- 1996 CB161 .B459 1996 Next 500 years : life in the coming millennium / Adrian Berry. 1982 E158 .A48 1982 America from the road / Reader's digest. Forbes, Steve, 1947- 1999 E885 .F67 1999 New birth of freedom : vision for America / Steve Forbes. G1019 .R47 1955 Rand McNally and Company. Standard world atlas. G70.4 .S77 1992 oversized Strain, Priscilla. Looking at earth / Priscilla Strain & Frederick Engle. 1992 GB55 .G313 Gaddum, Leonard William, Harold L. Knowles. 1953 Fairbridge, Rhodes W. GC9 .F3 (Rhodes Whitmore), 1914- 2006. Encyclopedia of oceanography, edited by Rhodes W. Fairbridge. Challenge of man's future; an inquiry concerning the condition of man during the GF31 .B68 Brown, Harrison, 1917-1986. years that lie ahead. GF47 .M63 Moran, Joseph M. [and] James H. Wiersma. 1973 Anderson, Walt, 1933- 1996 GN281.4 .A53 1996 Evolution isn't what it used to be : the augmented animal and the whole wired world / Walter Truett Anderson.
    [Show full text]
  • Physics Division Amuml Review
    Distribution Category: General Physics (UC-410) ANL-92/16 ANL—92/16 003038 ARGONNE NATIONAL LABORATORY 9700 South Cass Avenue Argonne, Illinois 60439-4801 PHYSICS DIVISION AMUML REVIEW April 1, 1991--March 31, 1992 Walter F. Henning Division Director August 1992 Preceding Annual Reviews ANL-89/11 1988-1989 ANL-90/18 1989-1990 ANL-91/12 1990-1991 Edited by Karen J. Thayer ii FOREWORD This past year has brought about several important developments for the ANL Physics Division. The new superconducting positive-ion injector (PII) for ATLAS has been completed and commissioned successfully. Just recently a uranium beam of excellent quality was accelerated to 5.7 MeV/u. The various activities from the aftermath of the Tiger Team visit have been completed and the research program at ATLAS has fully resumed under improved conditions and ~200 scientists and students participated in research at ATLAS during the year. Activities in Medium-Energy Physics aimed at an experimental program at CEBAF have accelerated with the cons- truction of the SOS spectrometer and the approval of several additional ANL experi- ments for the first phase of CEBAF operation. The atomic physics initiative towards a program at the Argonne Advanced Photon Source (APS) has been formulated and first experiments using the NSLS at Brookhaven, aimed at the additional development of the future program at the APS, have begun. The new superconducting positive-ion injector (PII) for ATLAS was completed and tested successfully for the first time during March by accelerating a beam of 40^rll+i The success of this test constitutes final proof of the technical sound- ness of this novel accelerator concept based on acceleration from very low vel- ocities by independently-phased superconducting resonators.
    [Show full text]