Chapter 10 Logistic Regression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On Assessing Binary Regression Models Based on Ungrouped Data
Biometrics 000, 1{18 DOI: 000 000 0000 On Assessing Binary Regression Models Based on Ungrouped Data Chunling Lu Division of Global Health, Brigham and Women's Hospital & Department of Global Health and Social Medicine Harvard University, Boston, U.S. email: chunling [email protected] and Yuhong Yang School of Statistics, University of Minnesota, Minnesota, U.S. email: [email protected] Summary: Assessing a binary regression model based on ungrouped data is a commonly encountered but very challenging problem. Although tests, such as Hosmer-Lemeshow test and le Cessie-van Houwelingen test, have been devised and widely used in applications, they often have low power in detecting lack of fit and not much theoretical justification has been made on when they can work well. In this paper, we propose a new approach based on a cross validation voting system to address the problem. In addition to a theoretical guarantee that the probabilities of type I and II errors both converge to zero as the sample size increases for the new method under proper conditions, our simulation results demonstrate that it performs very well. Key words: Goodness of fit; Hosmer-Lemeshow test; Model assessment; Model selection diagnostics. This paper has been submitted for consideration for publication in Biometrics Goodness of Fit for Ungrouped Data 1 1. Introduction 1.1 Motivation Parametric binary regression is one of the most widely used statistical tools in real appli- cations. A central component in parametric regression is assessment of a candidate model before accepting it as a satisfactory description of the data. In that regard, goodness of fit tests are needed to reveal significant lack-of-fit of the model to assess (MTA), if any. -

A Weakly Informative Default Prior Distribution for Logistic and Other
The Annals of Applied Statistics 2008, Vol. 2, No. 4, 1360–1383 DOI: 10.1214/08-AOAS191 c Institute of Mathematical Statistics, 2008 A WEAKLY INFORMATIVE DEFAULT PRIOR DISTRIBUTION FOR LOGISTIC AND OTHER REGRESSION MODELS By Andrew Gelman, Aleks Jakulin, Maria Grazia Pittau and Yu-Sung Su Columbia University, Columbia University, University of Rome, and City University of New York We propose a new prior distribution for classical (nonhierarchi- cal) logistic regression models, constructed by first scaling all nonbi- nary variables to have mean 0 and standard deviation 0.5, and then placing independent Student-t prior distributions on the coefficients. As a default choice, we recommend the Cauchy distribution with cen- ter 0 and scale 2.5, which in the simplest setting is a longer-tailed version of the distribution attained by assuming one-half additional success and one-half additional failure in a logistic regression. Cross- validation on a corpus of datasets shows the Cauchy class of prior dis- tributions to outperform existing implementations of Gaussian and Laplace priors. We recommend this prior distribution as a default choice for rou- tine applied use. It has the advantage of always giving answers, even when there is complete separation in logistic regression (a common problem, even when the sample size is large and the number of pre- dictors is small), and also automatically applying more shrinkage to higher-order interactions. This can be useful in routine data analy- sis as well as in automated procedures such as chained equations for missing-data imputation. We implement a procedure to fit generalized linear models in R with the Student-t prior distribution by incorporating an approxi- mate EM algorithm into the usual iteratively weighted least squares. -

Measures of Fit for Logistic Regression Paul D
Paper 1485-2014 SAS Global Forum Measures of Fit for Logistic Regression Paul D. Allison, Statistical Horizons LLC and the University of Pennsylvania ABSTRACT One of the most common questions about logistic regression is “How do I know if my model fits the data?” There are many approaches to answering this question, but they generally fall into two categories: measures of predictive power (like R-square) and goodness of fit tests (like the Pearson chi-square). This presentation looks first at R-square measures, arguing that the optional R-squares reported by PROC LOGISTIC might not be optimal. Measures proposed by McFadden and Tjur appear to be more attractive. As for goodness of fit, the popular Hosmer and Lemeshow test is shown to have some serious problems. Several alternatives are considered. INTRODUCTION One of the most frequent questions I get about logistic regression is “How can I tell if my model fits the data?” Often the questioner is expressing a genuine interest in knowing whether a model is a good model or a not-so-good model. But a more common motivation is to convince someone else--a boss, an editor, or a regulator--that the model is OK. There are two very different approaches to answering this question. One is to get a statistic that measures how well you can predict the dependent variable based on the independent variables. I’ll refer to these kinds of statistics as measures of predictive power. Typically, they vary between 0 and 1, with 0 meaning no predictive power whatsoever and 1 meaning perfect predictions. -
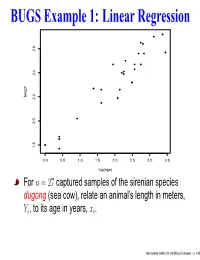
BUGS Example 1: Linear Regression Length 1.8 2.0 2.2 2.4 2.6
BUGS Example 1: Linear Regression length 1.8 2.0 2.2 2.4 2.6 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 log(age) For n = 27 captured samples of the sirenian species dugong (sea cow), relate an animal’s length in meters, Yi, to its age in years, xi. Intermediate WinBUGS and BRugs Examples – p. 1/35 BUGS Example 1: Linear Regression length 1.8 2.0 2.2 2.4 2.6 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 log(age) For n = 27 captured samples of the sirenian species dugong (sea cow), relate an animal’s length in meters, Yi, to its age in years, xi. To avoid a nonlinear model for now, transform xi to the log scale; plot of Y versus log(x) looks fairly linear! Intermediate WinBUGS and BRugs Examples – p. 1/35 Simple linear regression in WinBUGS Yi = β0 + β1 log(xi) + ǫi, i = 1,...,n iid where ǫ N(0,τ) and τ = 1/σ2, the precision in the data. i ∼ Prior distributions: flat for β0, β1 vague gamma on τ (say, Gamma(0.1, 0.1), which has mean 1 and variance 10) is traditional Intermediate WinBUGS and BRugs Examples – p. 2/35 Simple linear regression in WinBUGS Yi = β0 + β1 log(xi) + ǫi, i = 1,...,n iid where ǫ N(0,τ) and τ = 1/σ2, the precision in the data. i ∼ Prior distributions: flat for β0, β1 vague gamma on τ (say, Gamma(0.1, 0.1), which has mean 1 and variance 10) is traditional posterior correlation is reduced by centering the log(xi) around their own mean Intermediate WinBUGS and BRugs Examples – p. -

1D Regression Models Such As Glms
Chapter 4 1D Regression Models Such as GLMs ... estimates of the linear regression coefficients are relevant to the linear parameters of a broader class of models than might have been suspected. Brillinger (1977, p. 509) After computing β,ˆ one may go on to prepare a scatter plot of the points (βxˆ j, yj), j =1,...,n and look for a functional form for g( ). Brillinger (1983, p. 98) · This chapter considers 1D regression models including additive error re- gression (AER), generalized linear models (GLMs), and generalized additive models (GAMs). Multiple linear regression is a special case of these four models. See Definition 1.2 for the 1D regression model, sufficient predictor (SP = h(x)), estimated sufficient predictor (ESP = hˆ(x)), generalized linear model (GLM), and the generalized additive model (GAM). When using a GAM to check a GLM, the notation ESP may be used for the GLM, and EAP (esti- mated additive predictor) may be used for the ESP of the GAM. Definition 1.3 defines the response plot of ESP versus Y . Suppose the sufficient predictor SP = h(x). Often SP = xT β. If u only T T contains the nontrivial predictors, then SP = β1 + u β2 = α + u η is often T T T T T T used where β = (β1, β2 ) = (α, η ) and x = (1, u ) . 4.1 Introduction First we describe some regression models in the following three definitions. The most general model uses SP = h(x) as defined in Definition 1.2. The GAM with SP = AP will be useful for checking the model (often a GLM) with SP = xT β. -

The Overlooked Potential of Generalized Linear Models in Astronomy, I: Binomial Regression
Astronomy and Computing 12 (2015) 21–32 Contents lists available at ScienceDirect Astronomy and Computing journal homepage: www.elsevier.com/locate/ascom Full length article The overlooked potential of Generalized Linear Models in astronomy, I: Binomial regression R.S. de Souza a,∗, E. Cameron b, M. Killedar c, J. Hilbe d,e, R. Vilalta f, U. Maio g,h, V. Biffi i, B. Ciardi j, J.D. Riggs k, for the COIN collaboration a MTA Eötvös University, EIRSA ``Lendulet'' Astrophysics Research Group, Budapest 1117, Hungary b Department of Zoology, University of Oxford, Tinbergen Building, South Parks Road, Oxford, OX1 3PS, United Kingdom c Universitäts-Sternwarte München, Scheinerstrasse 1, D-81679, München, Germany d Arizona State University, 873701, Tempe, AZ 85287-3701, USA e Jet Propulsion Laboratory, 4800 Oak Grove Dr., Pasadena, CA 91109, USA f Department of Computer Science, University of Houston, 4800 Calhoun Rd., Houston TX 77204-3010, USA g INAF — Osservatorio Astronomico di Trieste, via G. Tiepolo 11, 34135 Trieste, Italy h Leibniz Institute for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany i SISSA — Scuola Internazionale Superiore di Studi Avanzati, Via Bonomea 265, 34136 Trieste, Italy j Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, D-85748 Garching, Germany k Northwestern University, Evanston, IL, 60208, USA article info a b s t r a c t Article history: Revealing hidden patterns in astronomical data is often the path to fundamental scientific breakthroughs; Received 26 September 2014 meanwhile the complexity of scientific enquiry increases as more subtle relationships are sought. Con- Accepted 2 April 2015 temporary data analysis problems often elude the capabilities of classical statistical techniques, suggest- Available online 29 April 2015 ing the use of cutting edge statistical methods. -

Generalized Linear Models I
Statistics 203: Introduction to Regression and Analysis of Variance Generalized Linear Models I Jonathan Taylor - p. 1/18 Today's class ● Today's class ■ Logistic regression. ● Generalized linear models ● Binary regression example ■ ● Binary outcomes Generalized linear models. ● Logit transform ■ ● Binary regression Deviance. ● Link functions: binary regression ● Link function inverses: binary regression ● Odds ratios & logistic regression ● Link & variance fns. of a GLM ● Binary (again) ● Fitting a binary regression GLM: IRLS ● Other common examples of GLMs ● Deviance ● Binary deviance ● Partial deviance tests 2 ● Wald χ tests - p. 2/18 Generalized linear models ● Today's class ■ All models we have seen so far deal with continuous ● Generalized linear models ● Binary regression example outcome variables with no restriction on their expectations, ● Binary outcomes ● Logit transform and (most) have assumed that mean and variance are ● Binary regression ● Link functions: binary unrelated (i.e. variance is constant). regression ● Link function inverses: binary ■ Many outcomes of interest do not satisfy this. regression ● Odds ratios & logistic ■ regression Examples: binary outcomes, Poisson count outcomes. ● Link & variance fns. of a GLM ● Binary (again) ■ A Generalized Linear Model (GLM) is a model with two ● Fitting a binary regression GLM: IRLS ingredients: a link function and a variance function. ● Other common examples of GLMs ◆ The link relates the means of the observations to ● Deviance ● Binary deviance predictors: linearization ● Partial deviance tests 2 ◆ ● Wald χ tests The variance function relates the means to the variances. - p. 3/18 Binary regression example ● Today's class ■ A local health clinic sent fliers to its clients to encourage ● Generalized linear models ● Binary regression example everyone, but especially older persons at high risk of ● Binary outcomes ● Logit transform complications, to get a flu shot in time for protection against ● Binary regression ● Link functions: binary an expected flu epidemic. -

Chapter 12 Generalized Linear Models
Chapter 12 Generalized Linear Models 12.1 Introduction Generalized linear models are an important class of parametric 1D regression models that include multiple linear regression, logistic regression and loglin- ear Poisson regression. Assume that there is a response variable Y and a k × 1 vector of nontrivial predictors x. Before defining a generalized linear model, the definition of a one parameter exponential family is needed. Let f(y) be a probability density function (pdf) if Y is a continuous random variable and let f(y) be a probability mass function (pmf) if Y is a discrete random variable. Assume that the support of the distribution of Y is Y and that the parameter space of θ is Θ. Definition 12.1. A family of pdfs or pmfs {f(y|θ):θ ∈ Θ} is a 1-parameter exponential family if f(y|θ)=k(θ)h(y)exp[w(θ)t(y)] (12.1) where k(θ) ≥ 0andh(y) ≥ 0. The functions h, k, t, and w are real valued functions. In the definition, it is crucial that k and w do not depend on y and that h and t do not depend on θ. The parameterization is not unique since, for example, w could be multiplied by a nonzero constant m if t is divided by m. Many other parameterizations are possible. If h(y)=g(y)IY(y), then usually k(θ)andg(y) are positive, so another parameterization is f(y|θ)=exp[w(θ)t(y)+d(θ)+S(y)]IY(y) (12.2) 401 where S(y)=log(g(y)),d(θ)=log(k(θ)), and the support Y does not depend on θ. -

NRT Lectures - Statistical Modeling
NRT Lectures - Statistical Modeling Generalized Linear Models Dr. Bo Li Department of Statistics University of Illinois at Urbana-Champaign Spring 2020 Slides credit to Dr. Trevor Park, Dr. Jeff Douglass and Dr. Steve Culpepper A linear model Y = α + β1x1 + ··· + βpxp + " | {z } E(Y ) = µ is usually not appropriate if Y is binary or a count. To go further, need regression-type models for binary or count-type responses. Assumed: Some exposure to linear regression and linear algebra. 1 The Generalized Linear Model (GLM) Seek to model independent observations Y1;:::;Yn of a response variable, in terms of corresponding vectors xi = (xi1; : : : ; xip) i = 1; : : : ; n of values of p explanatory variables. (All variables are represented by numbers, possibly some are dummy variables.) 2 I Systematic component: the linear predictor ηi = α + β1xi1 + ··· + βpxip with parameters α; β1; : : : ; βp (coefficients) Yi will depend on xi only through ηi I Random component: density of Yi from a natural exponential family f(yi; θi) = a(θi) b(yi) exp yi Q(θi) Q(θi) is the natural parameter. 3 I Random component: density of Yi from a natural exponential family f(yi; θi) = a(θi) b(yi) exp yi Q(θi) Q(θi) is the natural parameter. I Systematic component: the linear predictor ηi = α + β1xi1 + ··· + βpxip with parameters α; β1; : : : ; βp (coefficients) Yi will depend on xi only through ηi 3 I Link function: monotonic, differentiable g such that g(µi) = ηi where µi = E(Yi) Note: Ordinary linear models use the identity link: g(µ) = µ The canonical link satisfies g(µi) -

Linearized Binary Regression
Linearized Binary Regression Andrew S. Lan1, Mung Chiang2, and Christoph Studer3 1Princeton University, Princeton, NJ; [email protected] 2Purdue University, West Lafayette, IN; [email protected] 3Cornell University, Ithaca, NY; [email protected] Abstract—Probit regression was first proposed by Bliss in 1934 Section II-A. In what follows, we will assume that the noise to study mortality rates of insects. Since then, an extensive vector w 2 RM has i.i.d. standard normal entries, and refer body of work has analyzed and used probit or related binary to (1) as the standard probit model. regression methods (such as logistic regression) in numerous applications and fields. This paper provides a fresh angle to A. Relevant Prior Art such well-established binary regression methods. Concretely, we demonstrate that linearizing the probit model in combination with 1) Estimators: The two most common estimation techniques linear estimators performs on par with state-of-the-art nonlinear for the standard probit model in (1) are the posterior mean regression methods, such as posterior mean or maximum a- (PM) and maximum a-posteriori (MAP) estimators. The PM posteriori estimation, for a broad range of real-world regression estimator computes the following conditional expectation [9]: problems. We derive exact, closed-form, and nonasymptotic ex- pressions for the mean-squared error of our linearized estimators, PM R x^ = Ex[xjy] = N xp(xjy)dx; (2) which clearly separates them from nonlinear regression methods R that are typically difficult to analyze. We showcase the efficacy of where p(xjy) is the posterior probability of the vector x given our methods and results for a number of synthetic and real-world the observations y under the model (1). -

Bayesian Nonparametric Regression for Educational Research
Bayesian Nonparametric Regression for Educational Research George Karabatsos Professor of Educational Psychology Measurement, Evaluation, Statistics and Assessments University of Illinois-Chicago 2015 Annual Meeting Professional Development Course Thu, April 16, 8:00am to 3:45pm, Swissotel, Event Centre Second Level, Vevey 1&2 Supported by NSF-MMS Research Grant SES-1156372 Session 11.013 - Bayesian Nonparametric Regression for Educational Research Thu, April 16, 8:00am to 3:45pm, Swissotel, Event Centre Second Level, Vevey 1&2 Session Type: Professional Development Course Abstract Regression analysis is ubiquitous in educational research. However, the standard regression models can provide misleading results in data analysis, because they make assumptions that are often violated by real educational data sets. In order to provide an accurate regression analysis of a data set, it is necessary to specify a regression model that can describe all possible patterns of data. The Bayesian nonparametric (BNP) approach provides one possible way to construct such a flexible model, defined by an in…finite- mixture of regression models, that makes minimal assumptions about data. This one-day course will introduce participants to BNP regression models, in a lecture format. The course will also show how to apply the contemporary BNP models, in the analysis of real educational data sets, through guided hands-on exercises. The objective of this course is to show researchers how to use these BNP models for the accurate regression analysis of real educational data, involving either continuous, binary, ordinal, or censored dependent variables; for multi-level analysis, quantile regression analysis, density (distribution) regression analysis, causal analysis, meta-analysis, item response analysis, automatic predictor selection, cluster analysis, and survival analysis. -

Diagnosing Problems in Linear and Generalized Linear Models 6
Diagnosing Problems in Linear and Generalized Linear Models 6 egression diagnostics are methods for determining whether a fitted regres- R sion model adequately represents the data. We use the term regression broadly in this chapter to include methods for both linear and generalized lin- ear models, and many of the methods described here are also appropriate for other regression models. Because most of the methods for diagnosing prob- lems in linear models extend naturally to generalized linear models, we deal at greater length with linear-model diagnostics, briefly introducing the exten- sions to GLMs. Linear models fit by least squares make strong and sometimes unrealis- tic assumptions about the structure of the data. When these assumptions are violated, least-squares estimates can behave badly and may even completely misrepresent the data. Regression diagnostics can reveal such problems and often point the way toward solutions. Section 6.1 describes various kinds of residuals in linear models, and Section 6.2 introduces basic scatterplots of residuals, along with related plots that are used to assess the fit of a model to data. The remaining sections are specialized to particular problems, describing methods for diagnosis and at least touching on possible remedies. Section 6.3 introduces methods for detecting unusual data, including outliers, high-leverage points, and influen- tial observations. Section 6.4 returns to the topic of transformations of the response and predictors (discussed previously in Section 3.4) to correct prob- lems such as nonnormally distributed errors and nonlinearity. Section 6.5 deals with nonconstant error variance. Section 6.6 describes the extension of diagnostic methods to GLMs such as logistic and Poisson regression.