DOCSLIB.ORG

A Simulation Study of Goodness-Of-Fit Tests for Binary Regression with Applications to Norwegian Intensive Care Registry Data

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Simulation Study of Goodness-Of-Fit Tests for Binary Regression with Applications to Norwegian Intensive Care Registry Data A Simulation Study of Goodness-of-Fit Tests for Binary Regression with Applications to Norwegian Intensive Care Registry Data Ellisif Nygaard Supervisor: Geir Drage Berentsen Øystein A. Haaland Department of Mathematics University of Bergen This dissertation is submitted in partial fulfillment of the requirements for the degree of Master of Science in Statistics (Data Analysis) The Faculty of Mathematics and Natural Sciences January 2019 Acknowledgements I would like to thank my advisers Geir Drage Berentsen and Øystein Ariansen Haaland for introducing me to this topic and their guidance throughout the process of writing this thesis. I am also grateful to the Department of Heart Disease at Haukeland University Hospital for valuable experience, and their patience and generosity. In addition, I would like to thank the Norwegian Intensive Care Registry (NIR) for providing an unique data set. Many thanks to friends and family for their indispensable cheers of encouragement. I am also grateful for the proofreading and feedback received from Ranveig Nygaard. And I am grateful that this process is finally over. Abstract When using statistical methods to fit a model, the consensus is that it is possible to represent a complex reality in the form of a simpler model. It is helpful to systematically measure a model’s ability to capture the underlying system which controls the data generation in the population being examined. One of the possible tools we can apply to evaluate model adequacy is goodness-of- fit (GOF) tests. Summary GOF statistics are computed for a specific fitted model,then attributed an asymptotic distribution, and finally the null hypothesis that the model fits the data adequately is tested. A great challenge, when the model is a binary regression model and it has one or several continuous covariates, is to verify which asymptotic distributions the GOF statistics in fact have (Hosmer et al., 1997). In this thesis, we will evaluate the validity of the distributions of some established GOF test statistics mentioned in the literature. We have chosen so-called global GOF tests, where user input is not necessary. Tests demanding user input, such as the Hosmer-Lemeshow test, have been shown to have some considerable disadvantages. Hosmer et al.(1997) states that number of groups (which are determined by user discretion) can influence whether the GOF test rejects the model fit or not. Binary regression models present a specific set of challenges with regards toGOF measures, especially in situations where at least one covariate is continuous. There appears to be no broad general agreement on which GOF statistics are reliable options when fitting such models. This thesis aims to extend the current knowledge in this area. A modified version of one of the statistics is introduced. The GOF tests studied are later applied in a data analysis on real data set from the Norwegian Intensive Care Registry (NIR). An exploration was performed in the attempt to suggest a suitable tool to evaluate the discrepancies between the estimated logistic probabilities and the outcome variable, and how different GOF tests will behave for different categories of discrepancies. Table of contents Symbols xi 1 Introduction to Binary Regression1 1.1 The Classical Linear Regression Model . .1 1.2 Generalised Linear Models (GLMs) . .2 1.3 Binary Regression Models . .4 1.3.1 Link Functions and Their Corresponding Models . .4 1.3.2 Interpretation of logistic regression models . .6 1.3.3 Maximum Likelihood Estimation . .7 2 Goodness-of-Fit Tests and Their Statistics9 2.1 The Standardized Pearson Test . .9 2.2 Unweighted Sum of Squares Test . 11 2.3 Stukel’s Test . 12 2.4 The Information Matrix Test . 14 3 Significance Level Study 19 3.1 The Goodness-of-Fit Statistics and Their Implementation . 20 3.2 A Weibull-based behaviour indicator . 22 3.3 Significance Level Study . 24 3.4 The results of the significance level study . 27 viii Table of contents 3.5 Study of the Weibull-based behaviour indicator applied to simulation data . 30 3.5.1 Principal Component Analysis . 34 3.5.2 The Weibull shape parameter and standard deviation as potential indicators of empirical significance levels . 39 3.5.3 Future work . 42 4 Power Study 43 4.1 Types of departure . 43 4.2 A General Outline of the Power Study Design . 44 4.3 Details of the power study design . 46 4.3.1 Departure type D1: Omission of a quadratic term . 47 4.3.2 Departure type D2: Omission of a log term . 49 4.3.3 Departure type D3: Omission of the main effect of a binary covariate and its interaction with a continuous covariate. 52 4.3.4 Departure type D4: Selection of an incorrect link function. 54 4.4 The Results of the Power Study . 58 4.4.1 Power assessment results for departure type D1 ........... 58 4.4.2 Power assessment results for departure type D2 ........... 60 4.4.3 Power assessment results for departure type D3 ........... 62 4.4.4 Power assessment results for departure type D4 ........... 63 5 Summary of Simulation Studies 65 5.1 The empirical significance levels of the GOF test statistics . 65 5.2 The empirical power of the GOF test statistics . 67 5.2.1 Omission of a quadratic term . 67 5.2.2 Omission of a log term . 68 5.2.3 Omission of the main effect of a binary covariate and its interaction with a continuous covariate . 68 5.2.4 Incorrectly specified link function . 69 Table of contents ix 5.2.5 Summary and recommendations . 70 6 Data Analysis 71 6.1 Background . 71 6.2 The Data Set . 72 6.3 Methods . 74 6.3.1 The models . 74 6.4 Statistical analysis . 76 6.5 Results . 77 Bibliography 85 Symbols Roman Symbols H0 The null hypothesis M0 The true logistic model Sˆst The standardised USS statistic 2 Xst The standardised Pearson chi-square statistic Greek Symbols j1, j2 The shape parameters of Stukel’s generalised model Acronyms / Abbreviations GOF Goodness-of-fit IMT Information matrix test LPM Linear probability model LRT Likelihood ratio test ML Maximum likelihood NIR The Norwegian Intensive Care Registry PRD Predicted risk of death USS Unweighted sum-of-squares Chapter 1 Introduction to Binary Regression 1.1 The Classical Linear Regression Model Let the data (yi;xi1;:::;xik), i = 1;:::;n, consist of n observations of the continuous response variable y and the k covariates x1;:::;xk. The covariates can be continuous or categorical. In Fahrmeir et al.(2013), the classical linear regression model is given by yi = b0 + b1xi1 + ::: + bkxik + ei; i = 1;:::;n; where the error terms e1;e2;:::;en are assumed to be independent and identically normally 2 distributed with E(ei) = 0 and Var(ei) = s . The model is linear in the parameters b0;:::;bk, whereas the covariates can be non-linear expressions. The following quantity, which represents the influence the covariates have on the model, is referred to as a linear predictor: T hi = b0 + b1xi1 + ::: + bkxik = xi b , (1.1) T T where xi = [1 xi1 xi2 ::: xik] and b = [b0 b1 ::: bk] . This can be expressed in vector form as y = X b + e, and (1.2) E(y) = m = X b , (1.3) 2 Introduction to Binary Regression T T where y = [y1 y2 ::: yn] , and m = [m1 m2 ::: mn] . The matrix X , which is often called the design matrix, is defined as 2 3 2 T3 1 x11 x12 ··· x1k x1 6 7 6 T7 61 x21 x22 ··· x2k7 6x2 7 X = 6. 7 = 6 . 7, 6. ... 7 6 . 7 4. 5 4 . 5 T 1 xn1 xn2 ··· xnk xn and X b is the linear component of the classical linear regression model. In this setting, the ordinary least squares (OLS) estimate and the maximum likelihood estimate (MLE) of b are identical, and given by bˆ = (X TX )−1X Ty. (1.4) Once the model parameters have been fitted to the data in X , the linear combinations of b and the rows of the design matrix comprise the estimated linear predictors: T ˆ ˆ ˆ ˆ hˆi = xi b = b0 + b1xi1 + ::: + bkxik. (1.5) Due to the model assumptions, the estimated linear predictors are suitable estimators for E(yi) = E(yijxi1;:::;xik) = E(b0 +b1xi1 +:::+bkxik +ei) = b0 +b1xi1 +:::+bkxik. Hence ˆ hˆi is used to predict yi, i.e. yˆ = X b . The classical linear regression is applied in prediction, forecasting, and when quantifying the strength of linear relationships. 1.2 Generalised Linear Models (GLMs) Classical linear regression models can be generalised in order to permit response variables whose errors are not normally distributed. GLMs are extensions of linear models which facilitate modelling non-normal response variables. A GLM consists of three components: 1) The random component, 2) the systematic component, and 3) the link function. The response variables Y1;:::;Yn are the random component. A standard assumption is that the response variables are random and independent, but not identically distributed. They each have a distribution in canonical form from the same exponential family. In some cases, 1.2 Generalised Linear Models (GLMs) 3 the observations of Y1;:::;Yn are binary, taking on values such as "0" and "1", or "success" and "failure". The systematic component is the function of the covariates x1;:::;xk which is related to the expected value of Y1;:::;Yn. Just as in classical linear regression, the function is called the linear predictor and takes the usual form: T hi = b0 + b1xi1 + ::: + bkxik = xi b , (1.6) T T where, as before, xi = [1 xi1 xi2 ::: xik] and b = [b0 b1 ::: bk] . Finally, the link function connects the random component and the systematic component by stating that T g(mi) = xi b , (1.7) where mi = E(Yi) and g(·) is the link function.
Load more

Recommended publications
  • On Assessing Binary Regression Models Based on Ungrouped Data
    Biometrics 000, 1{18 DOI: 000 000 0000 On Assessing Binary Regression Models Based on Ungrouped Data Chunling Lu Division of Global Health, Brigham and Women's Hospital & Department of Global Health and Social Medicine Harvard University, Boston, U.S. email: chunling [email protected] and Yuhong Yang School of Statistics, University of Minnesota, Minnesota, U.S. email: [email protected] Summary: Assessing a binary regression model based on ungrouped data is a commonly encountered but very challenging problem. Although tests, such as Hosmer-Lemeshow test and le Cessie-van Houwelingen test, have been devised and widely used in applications, they often have low power in detecting lack of fit and not much theoretical justification has been made on when they can work well. In this paper, we propose a new approach based on a cross validation voting system to address the problem. In addition to a theoretical guarantee that the probabilities of type I and II errors both converge to zero as the sample size increases for the new method under proper conditions, our simulation results demonstrate that it performs very well. Key words: Goodness of fit; Hosmer-Lemeshow test; Model assessment; Model selection diagnostics. This paper has been submitted for consideration for publication in Biometrics Goodness of Fit for Ungrouped Data 1 1. Introduction 1.1 Motivation Parametric binary regression is one of the most widely used statistical tools in real appli- cations. A central component in parametric regression is assessment of a candidate model before accepting it as a satisfactory description of the data. In that regard, goodness of fit tests are needed to reveal significant lack-of-fit of the model to assess (MTA), if any.
    [Show full text]
  • 05 36534Nys130620 31
    Monte Carlos study on Power Rates of Some Heteroscedasticity detection Methods in Linear Regression Model with multicollinearity problem O.O. Alabi, Kayode Ayinde, O. E. Babalola, and H.A. Bello Department of Statistics, Federal University of Technology, P.M.B. 704, Akure, Ondo State, Nigeria Corresponding Author: O. O. Alabi, [email protected] Abstract: This paper examined the power rate exhibit by some heteroscedasticity detection methods in a linear regression model with multicollinearity problem. Violation of unequal error variance assumption in any linear regression model leads to the problem of heteroscedasticity, while violation of the assumption of non linear dependency between the exogenous variables leads to multicollinearity problem. Whenever these two problems exist one would faced with estimation and hypothesis problem. in order to overcome these hurdles, one needs to determine the best method of heteroscedasticity detection in other to avoid taking a wrong decision under hypothesis testing. This then leads us to the way and manner to determine the best heteroscedasticity detection method in a linear regression model with multicollinearity problem via power rate. In practices, variance of error terms are unequal and unknown in nature, but there is need to determine the presence or absence of this problem that do exist in unknown error term as a preliminary diagnosis on the set of data we are to analyze or perform hypothesis testing on. Although, there are several forms of heteroscedasticity and several detection methods of heteroscedasticity, but for any researcher to arrive at a reasonable and correct decision, best and consistent performed methods of heteroscedasticity detection under any forms or structured of heteroscedasticity must be determined.
    [Show full text]
  • The Effects of Simplifying Assumptions in Power Analysis
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Public Access Theses and Dissertations from Education and Human Sciences, College of the College of Education and Human Sciences (CEHS) 4-2011 The Effects of Simplifying Assumptions in Power Analysis Kevin A. Kupzyk University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/cehsdiss Part of the Educational Psychology Commons Kupzyk, Kevin A., "The Effects of Simplifying Assumptions in Power Analysis" (2011). Public Access Theses and Dissertations from the College of Education and Human Sciences. 106. https://digitalcommons.unl.edu/cehsdiss/106 This Article is brought to you for free and open access by the Education and Human Sciences, College of (CEHS) at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Public Access Theses and Dissertations from the College of Education and Human Sciences by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Kupzyk - i THE EFFECTS OF SIMPLIFYING ASSUMPTIONS IN POWER ANALYSIS by Kevin A. Kupzyk A DISSERTATION Presented to the Faculty of The Graduate College at the University of Nebraska In Partial Fulfillment of Requirements For the Degree of Doctor of Philosophy Major: Psychological Studies in Education Under the Supervision of Professor James A. Bovaird Lincoln, Nebraska April, 2011 Kupzyk - i THE EFFECTS OF SIMPLIFYING ASSUMPTIONS IN POWER ANALYSIS Kevin A. Kupzyk, Ph.D. University of Nebraska, 2011 Adviser: James A. Bovaird In experimental research, planning studies that have sufficient probability of detecting important effects is critical. Carrying out an experiment with an inadequate sample size may result in the inability to observe the effect of interest, wasting the resources spent on an experiment.
    [Show full text]
  • Introduction to Hypothesis Testing
    Introduction to Hypothesis Testing OPRE 6301 Motivation . The purpose of hypothesis testing is to determine whether there is enough statistical evidence in favor of a certain belief, or hypothesis, about a parameter. Examples: Is there statistical evidence, from a random sample of potential customers, to support the hypothesis that more than 10% of the potential customers will pur- chase a new product? Is a new drug effective in curing a certain disease? A sample of patients is randomly selected. Half of them are given the drug while the other half are given a placebo. The conditions of the patients are then mea- sured and compared. These questions/hypotheses are similar in spirit to the discrimination example studied earlier. Below, we pro- vide a basic introduction to hypothesis testing. 1 Criminal Trials . The basic concepts in hypothesis testing are actually quite analogous to those in a criminal trial. Consider a person on trial for a “criminal” offense in the United States. Under the US system a jury (or sometimes just the judge) must decide if the person is innocent or guilty while in fact the person may be innocent or guilty. These combinations are summarized in the table below. Person is: Innocent Guilty Jury Says: Innocent No Error Error Guilty Error No Error Notice that there are two types of errors. Are both of these errors equally important? Or, is it as bad to decide that a guilty person is innocent and let them go free as it is to decide an innocent person is guilty and punish them for the crime? Or, is a jury supposed to be totally objective, not assuming that the person is either innocent or guilty and make their decision based on the weight of the evidence one way or another? 2 In a criminal trial, there actually is a favored assump- tion, an initial bias if you will.
    [Show full text]
  • Power of a Statistical Test
    Power of a Statistical Test By Smita Skrivanek, Principal Statistician, MoreSteam.com LLC What is the power of a test? The power of a statistical test gives the likelihood of rejecting the null hypothesis when the null hypothesis is false. Just as the significance level (alpha) of a test gives the probability that the null hypothesis will be rejected when it is actually true (a wrong decision), power quantifies the chance that the null hypothesis will be rejected when it is actually false (a correct decision). Thus, power is the ability of a test to correctly reject the null hypothesis. Why is it important? Although you can conduct a hypothesis test without it, calculating the power of a test beforehand will help you ensure that the sample size is large enough for the purpose of the test. Otherwise, the test may be inconclusive, leading to wasted resources. On rare occasions the power may be calculated after the test is performed, but this is not recommended except to determine an adequate sample size for a follow-up study (if a test failed to detect an effect, it was obviously underpowered – nothing new can be learned by calculating the power at this stage). How is it calculated? As an example, consider testing whether the average time per week spent watching TV is 4 hours versus the alternative that it is greater than 4 hours. We will calculate the power of the test for a specific value under the alternative hypothesis, say, 7 hours: The Null Hypothesis is H0: μ = 4 hours The Alternative Hypothesis is H1: μ = 6 hours Where μ = the average time per week spent watching TV.
    [Show full text]
  • Confidence Intervals and Hypothesis Tests
    Chapter 2 Confidence intervals and hypothesis tests This chapter focuses on how to draw conclusions about populations from sample data. We'll start by looking at binary data (e.g., polling), and learn how to estimate the true ratio of 1s and 0s with confidence intervals, and then test whether that ratio is significantly different from some baseline value using hypothesis testing. Then, we'll extend what we've learned to continuous measurements. 2.1 Binomial data Suppose we're conducting a yes/no survey of a few randomly sampled people 1, and we want to use the results of our survey to determine the answers for the overall population. 2.1.1 The estimator The obvious first choice is just the fraction of people who said yes. Formally, suppose we have samples x1,..., xn that can each be 0 or 1, and the probability that each xi is 1 is p (in frequentist style, we'll assume p is fixed but unknown: this is what we're interested in finding). We'll assume our samples are indendepent and identically distributed (i.i.d.), meaning that each one has no dependence on any of the others, and they all have the same probability p of being 1. Then our estimate for p, which we'll callp ^, or \p-hat" would be n 1 X p^ = x : n i i=1 Notice thatp ^ is a random quantity, since it depends on the random quantities xi. In statistical lingo,p ^ is known as an estimator for p. Also notice that except for the factor of 1=n in front, p^ is almost a binomial random variable (in particular, (np^) ∼ B(n; p)).
    [Show full text]
  • A Weakly Informative Default Prior Distribution for Logistic and Other
    The Annals of Applied Statistics 2008, Vol. 2, No. 4, 1360–1383 DOI: 10.1214/08-AOAS191 c Institute of Mathematical Statistics, 2008 A WEAKLY INFORMATIVE DEFAULT PRIOR DISTRIBUTION FOR LOGISTIC AND OTHER REGRESSION MODELS By Andrew Gelman, Aleks Jakulin, Maria Grazia Pittau and Yu-Sung Su Columbia University, Columbia University, University of Rome, and City University of New York We propose a new prior distribution for classical (nonhierarchi- cal) logistic regression models, constructed by first scaling all nonbi- nary variables to have mean 0 and standard deviation 0.5, and then placing independent Student-t prior distributions on the coefficients. As a default choice, we recommend the Cauchy distribution with cen- ter 0 and scale 2.5, which in the simplest setting is a longer-tailed version of the distribution attained by assuming one-half additional success and one-half additional failure in a logistic regression. Cross- validation on a corpus of datasets shows the Cauchy class of prior dis- tributions to outperform existing implementations of Gaussian and Laplace priors. We recommend this prior distribution as a default choice for rou- tine applied use. It has the advantage of always giving answers, even when there is complete separation in logistic regression (a common problem, even when the sample size is large and the number of pre- dictors is small), and also automatically applying more shrinkage to higher-order interactions. This can be useful in routine data analy- sis as well as in automated procedures such as chained equations for missing-data imputation. We implement a procedure to fit generalized linear models in R with the Student-t prior distribution by incorporating an approxi- mate EM algorithm into the usual iteratively weighted least squares.
    [Show full text]
  • Understanding Statistical Hypothesis Testing: the Logic of Statistical Inference
    Review Understanding Statistical Hypothesis Testing: The Logic of Statistical Inference Frank Emmert-Streib 1,2,* and Matthias Dehmer 3,4,5 1 Predictive Society and Data Analytics Lab, Faculty of Information Technology and Communication Sciences, Tampere University, 33100 Tampere, Finland 2 Institute of Biosciences and Medical Technology, Tampere University, 33520 Tampere, Finland 3 Institute for Intelligent Production, Faculty for Management, University of Applied Sciences Upper Austria, Steyr Campus, 4040 Steyr, Austria 4 Department of Mechatronics and Biomedical Computer Science, University for Health Sciences, Medical Informatics and Technology (UMIT), 6060 Hall, Tyrol, Austria 5 College of Computer and Control Engineering, Nankai University, Tianjin 300000, China * Correspondence: [email protected]; Tel.: +358-50-301-5353 Received: 27 July 2019; Accepted: 9 August 2019; Published: 12 August 2019 Abstract: Statistical hypothesis testing is among the most misunderstood quantitative analysis methods from data science. Despite its seeming simplicity, it has complex interdependencies between its procedural components. In this paper, we discuss the underlying logic behind statistical hypothesis testing, the formal meaning of its components and their connections. Our presentation is applicable to all statistical hypothesis tests as generic backbone and, hence, useful across all application domains in data science and artificial intelligence. Keywords: hypothesis testing; machine learning; statistics; data science; statistical inference 1. Introduction We are living in an era that is characterized by the availability of big data. In order to emphasize the importance of this, data have been called the ‘oil of the 21st Century’ [1]. However, for dealing with the challenges posed by such data, advanced analysis methods are needed.
    [Show full text]
  • Measures of Fit for Logistic Regression Paul D
    Paper 1485-2014 SAS Global Forum Measures of Fit for Logistic Regression Paul D. Allison, Statistical Horizons LLC and the University of Pennsylvania ABSTRACT One of the most common questions about logistic regression is “How do I know if my model fits the data?” There are many approaches to answering this question, but they generally fall into two categories: measures of predictive power (like R-square) and goodness of fit tests (like the Pearson chi-square). This presentation looks first at R-square measures, arguing that the optional R-squares reported by PROC LOGISTIC might not be optimal. Measures proposed by McFadden and Tjur appear to be more attractive. As for goodness of fit, the popular Hosmer and Lemeshow test is shown to have some serious problems. Several alternatives are considered. INTRODUCTION One of the most frequent questions I get about logistic regression is “How can I tell if my model fits the data?” Often the questioner is expressing a genuine interest in knowing whether a model is a good model or a not-so-good model. But a more common motivation is to convince someone else--a boss, an editor, or a regulator--that the model is OK. There are two very different approaches to answering this question. One is to get a statistic that measures how well you can predict the dependent variable based on the independent variables. I’ll refer to these kinds of statistics as measures of predictive power. Typically, they vary between 0 and 1, with 0 meaning no predictive power whatsoever and 1 meaning perfect predictions.
    [Show full text]
  • Post Hoc Power: Tables and Commentary
    Post Hoc Power: Tables and Commentary Russell V. Lenth July, 2007 The University of Iowa Department of Statistics and Actuarial Science Technical Report No. 378 Abstract Post hoc power is the retrospective power of an observed effect based on the sample size and parameter estimates derived from a given data set. Many scientists recommend using post hoc power as a follow-up analysis, especially if a finding is nonsignificant. This article presents tables of post hoc power for common t and F tests. These tables make it explicitly clear that for a given significance level, post hoc power depends only on the P value and the degrees of freedom. It is hoped that this article will lead to greater understanding of what post hoc power is—and is not. We also present a “grand unified formula” for post hoc power based on a reformulation of the problem, and a discussion of alternative views. Key words: Post hoc power, Observed power, P value, Grand unified formula 1 Introduction Power analysis has received an increasing amount of attention in the social-science literature (e.g., Cohen, 1988; Bausell and Li, 2002; Murphy and Myors, 2004). Used prospectively, it is used to determine an adequate sample size for a planned study (see, for example, Kraemer and Thiemann, 1987); for a stated effect size and significance level for a statistical test, one finds the sample size for which the power of the test will achieve a specified value. Many studies are not planned with such a prospective power calculation, however; and there is substantial evidence (e.g., Mone et al., 1996; Maxwell, 2004) that many published studies in the social sciences are under-powered.
    [Show full text]
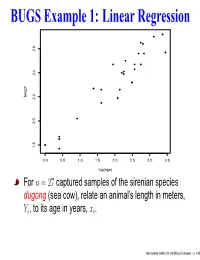
  • BUGS Example 1: Linear Regression Length 1.8 2.0 2.2 2.4 2.6
    BUGS Example 1: Linear Regression length 1.8 2.0 2.2 2.4 2.6 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 log(age) For n = 27 captured samples of the sirenian species dugong (sea cow), relate an animal’s length in meters, Yi, to its age in years, xi. Intermediate WinBUGS and BRugs Examples – p. 1/35 BUGS Example 1: Linear Regression length 1.8 2.0 2.2 2.4 2.6 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 log(age) For n = 27 captured samples of the sirenian species dugong (sea cow), relate an animal’s length in meters, Yi, to its age in years, xi. To avoid a nonlinear model for now, transform xi to the log scale; plot of Y versus log(x) looks fairly linear! Intermediate WinBUGS and BRugs Examples – p. 1/35 Simple linear regression in WinBUGS Yi = β0 + β1 log(xi) + ǫi, i = 1,...,n iid where ǫ N(0,τ) and τ = 1/σ2, the precision in the data. i ∼ Prior distributions: flat for β0, β1 vague gamma on τ (say, Gamma(0.1, 0.1), which has mean 1 and variance 10) is traditional Intermediate WinBUGS and BRugs Examples – p. 2/35 Simple linear regression in WinBUGS Yi = β0 + β1 log(xi) + ǫi, i = 1,...,n iid where ǫ N(0,τ) and τ = 1/σ2, the precision in the data. i ∼ Prior distributions: flat for β0, β1 vague gamma on τ (say, Gamma(0.1, 0.1), which has mean 1 and variance 10) is traditional posterior correlation is reduced by centering the log(xi) around their own mean Intermediate WinBUGS and BRugs Examples – p.
    [Show full text]
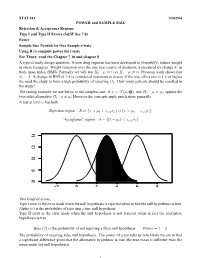
  • STAT 141 11/02/04 POWER and SAMPLE SIZE Rejection & Acceptance Regions Type I and Type II Errors (S&W Sec 7.8) Power
    STAT 141 11/02/04 POWER and SAMPLE SIZE Rejection & Acceptance Regions Type I and Type II Errors (S&W Sec 7.8) Power Sample Size Needed for One Sample z-tests. Using R to compute power for t.tests For Thurs: read the Chapter 7.10 and chapter 8 A typical study design question: A new drug regimen has been developed to (hopefully) reduce weight in obese teenagers. Weight reduction over the one year course of treatment is measured by change X in body mass index (BMI). Formally we will test H0 : µ = 0 vs H1 : µ 6= 0. Previous work shows that σx = 2. A change in BMI of 1.5 is considered important to detect (if the true effect size is 1.5 or higher we need the study to have a high probability of rejecting H0. How many patients should be enrolled in the study? σ2 The testing example we use below is the simplest one: if x¯ ∼ N(µ, n ), test H0 : µ = µ0 against the two-sided alternative H1 : µ 6= µ0 However the concepts apply much more generally. A test at level α has both: Rejection region : R = {x¯ > µ0 + zα/2σx¯} ∪ {x¯ < µ0 − zα/2σx¯} “Acceptance” region : A = {|x¯ − µ0| < zα/2σx¯} 0.4 0.4 0.3 0.3 0.2 0.2 0.1 0.1 0.0 0.0 −2 0 2 4 6 8 Two kinds of errors: Type I error is the error made when the null hypothesis is rejected when in fact the null hypothesis is true.
    [Show full text]