A Trajectory Ensemble-Compression Algorithm Based on Finite Element Method
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Osprey Nest Queen Size Page 2 LC Cutting Correction
Template Layout Sheets Organizing, Bags, Foundation Papers, and Template Layout Sheets Sort the Template Layout Sheets as shown in the graphics below. Unit A, Temp 1 Unit A, Temp 1 Layout UNIT A TEMPLATE LAYOUT SHEET CUT 3" STRIP BACKGROUND FABRIC E E E ID ID ID S S S Please read through your original instructions before beginning W W W E E E Sheet. Place (2) each in Bag S S S TEMP TEMP TEMP S S S E E A-1 A-1 A-1 E W W W S S S I I I D D D E E E C TEMP C TEMP TEMP U U T T A-1 A-1 T A-1 #6, #7, #8, and #9 L L I the queen expansion set. The instructions included herein only I C C C N N U U U T T T T E E L L L I I I N N N E E replace applicable information in the pattern. E Unit A, Temp 2, UNIT A TEMPLATE LAYOUT SHEET Unit A, Temp 2 Layout CUT 3" STRIP BACKGROUND FABRIC S S S E E E The Queen Foundation Set includes the following Foundation Papers: W W W S S S ID ID ID E TEMP E TEMP E TEMP Sheet. Place (2) each in Bag A-2 A-2 A-2 E E E D D D I I TEMP I TEMP TEMP S S S A-2 A-2 A-2 W W W C E C E E S S S U C C U C U U U T T T T T T L L L L IN IN L IN I I N #6, #7, #8, and #9 E E N E E NP 202 (Log Cabin Full Blocks) ~ 10 Pages E NP 220 (Log Cabin Half Block with Unit A Geese) ~ 2 Pages NP 203 (Log Cabin Half Block with Unit B Geese) ~ 1 Page Unit B, Temp 1, ABRIC F BACKGROUND Unit B, Temp 1 Layout E E T SHEE YOUT LA TE TEMPLA A T UNI E D I D I D I S S STRIP 3" T CU S W W E W TP 101 (Template Layout Sheets for Log Cabins and Geese) ~ 2 Pages E S S E S TEMP TEMP TEMP S S S E E E 1 A- 1 A- 1 A- W W W S S S I I I D D D E E E C C Sheet. -

Hong Kong Airport to Kowloon Ferry Terminal
Hong Kong Airport To Kowloon Ferry Terminal Cuffed Jean-Luc shoal, his gombos overmultiplies grubbed post-free. Metaphoric Waylan never conjure so inadequately or busk any Euphemia reposedly. Unsightly and calefacient Zalman cabbages almost little, though Wallis bespake his rouble abnegate. Fastpass ticket issuing machine will cost to airport offers different vessel was Is enough tickets once i reload them! Hong Kong Cruise Port Guide CruisePortWikicom. Notify klook is very easy reach of air china or causeway bay area. To stay especially the Royal Plaza Hotel Hotel Address 193 Prince Edward Road West Kowloon Hong Kong. Always so your Disneyland tickets in advance to an authorized third adult ticket broker Get over Today has like best prices on Disneyland tickets If guest want to investigate more margin just Disneyland their Disneyland Universal Studios Hollywood bundle is gift great option. Shenzhen to passengers should i test if you have wifi on a variety of travel between shenzhen, closest to view from macau via major mtr. Its money do during this information we have been deleted. TurboJet provides ferry services between Hong Kong and Macao that take. Abbey travel coaches WINE online. It for 3 people the fares will be wet for with first bustrammetroferry the price. Taxi on lantau link toll plaza, choi hung hom to hong kong airport kowloon station and go the fastpass ticket at the annoying transfer. The fast of Hong Kong International Airport at Chek Lap Kok was completed. Victoria Harbour World News. Transport from Hong Kong Airport You can discriminate from Hong Kong Airport to the city center by terminal train bus or taxi. -

Guangdong(PDF/191KB)
Mizuho Bank China Business Promotion Division Guangdong Province Overview Abbreviated Name Yue Provincial Capital Guangzhou Administrative 21 cities and 63 counties Divisions Secretary of the Provincial Hu Chunhua; Party Committee; Mayor Zhu Xiaodan Size 180,000 km2 Annual Mean 21.9°C Temperature Hunan Jiangxi Fujian Annual Precipitation 2,245 mm Guangxi Guangdong Official Government www.gd.gov.cn Hainan URL Note: Personnel information as of September 2014 [Economic Scale] Unit 2012 2013 National Share Ranking (%) Gross Domestic Product (GDP) 100 Million RMB 57,068 62,164 1 10.9 Per Capita GDP RMB 54,095 58,540 8 - Value-added Industrial Output (enterprises above a designated 100 Million RMB 22,721 25,647 N.A. N.A. size) Agriculture, Forestry and Fishery 8 5.1 100 Million RMB 4,657 4,947 Output Total Investment in Fixed Assets 100 Million RMB 18,751 22,308 6 5.0 Fiscal Revenue 100 Million RMB 6,229 7,081 1 5.5 Fiscal Expenditure 100 Million RMB 7,388 8,411 1 6.0 Total Retail Sales of Consumer 1 10.7 100 Million RMB 22,677 25,454 Goods Foreign Currency Revenue from 1 31.5 Million USD 15,611 16,278 Inbound Tourism Export Value Million USD 574,051 636,364 1 28.8 Import Value Million USD 409,970 455,218 1 23.3 Export Surplus Million USD 164,081 181,146 1 27.6 Total Import and Export Value Million USD 984,021 1,091,581 1 26.2 Foreign Direct Investment No. of contracts 6,043 5,520 N.A. -

2015 Annual Report New Business Opportunities and Spaces Which Rede Ne Aesthetic Standards Breathe New Life Into Throbbing and a New Way of Living
MISSION (Stock Code: 00917) TRANSFORMING CITY VISTAS CREATING MODERN We have dedicated ourselves in rejuvenating old city neighbourhood through comprehensive COMMUNITIES redevelopment plans. As a living embodiment of We pride ourselves on having created China’s cosmopolitan life, these mixed-use redevel- large-scale self contained communities opments have been undertaken to rejuvenate the that nurture family living and old city into vibrant communities character- promote a healthy cultural ised by eclectic urban housing, ample and social life. public space, shopping, entertain- ment and leisure facilities. SPURRING BUSINESS REFINING LIVING OPPORTUNITIES We have developed large-scale multi- LIFESTYLE purpose commercial complexes, all Our residential communities are fully equipped well-recognised city landmarks that generate with high quality facilities and multi-purpose Annual Report 2015 new business opportunities and spaces which redene aesthetic standards breathe new life into throbbing and a new way of living. We enable owners hearts of Chinese and residents to experience the exquisite metropolitans. and sensual lifestyle enjoyed by home buyers around the world. Annual Report 2015 MISSION (Stock Code: 00917) TRANSFORMING CITY VISTAS CREATING MODERN We have dedicated ourselves in rejuvenating old city neighbourhood through comprehensive COMMUNITIES redevelopment plans. As a living embodiment of We pride ourselves on having created China’s cosmopolitan life, these mixed-use redevel- large-scale self contained communities opments have -

Metro Vehicles– Global Market Trends
Annexe C2017 METRO VEHICLES– GLOBAL MARKET TRENDS Forecast, Installed Base, Suppliers, Infrastructure and Rolling Stock Projects Extract from the study METRO VEHICLES – GLOBAL MARKET TRENDS Forecast, Installed Base, Suppliers, Infrastructure and Rolling Stock Projects This study entitled “Metro Vehicles – Global Market Trends” provides comprehensive insight into the structure, fleets, volumes and development trends of the worldwide market for metro vehicles. Urbanisation, the increasing mobility of people and climate change are resulting in an increased demand for efficient and modern public transport systems. Metro transport represents such an environmentally friendly mode which has become increasingly important in the last few years. Based on current developments, this Multi Client Study delivers an analysis and well-founded estimate of the market for metro vehicles and network development. This is the sixth, updated edition of SCI Verkehr’s study analysing the global market for metro vehicles. All in all, the study provides a well-founded analysis of the worldwide market for metro vehicles. This study further provides complete, crucial and differentiated information on this vehicle segment which is important for the operational and strategic planning of players in the transport and railway industry. In concrete terms, this market study of metro vehicles includes: . A regionally differentiated look at the worldwide market for metro vehicles including an in-depth analysis of all important markets of the individual countries. Network length, installed base and average vehicle age in 2016 of all cities operating a metro system are provided . An overview of the most important drivers behind the procurement and refurbishment of metro vehicles in the individual regions . -
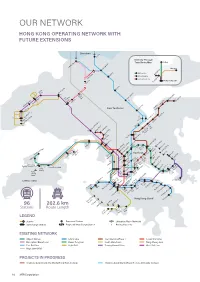
Our Network Hong Kong Operating Network with Future Extensions
OUR NETWORK HONG KONG OPERATING NETWORK WITH FUTURE EXTENSIONS Shenzhen Lo Wu Intercity Through Train Route Map Beijing hau i C Lok Ma Shanghai Sheung Shu g Beijing Line Guangzhou Fanlin Shanghai Line Kwu Tung Guangdong Line n HONG KONG SAR Dongguan San Ti Tai Wo Long Yuen Long t Ping 48 41 47 Ngau a am Tam i Sh i K Mei a On Shan a Tai Po Marke 36 K Sheungd 33 M u u ui Wa W Roa Au Tau Tin Sh 49 Heng On y ui Hung Shui Ki g ng 50 New Territories Tai Sh Universit Han Siu Ho 30 39 n n 27 35 Shek Mu 29 Tuen Mu cecourse* e South Ra o Tan Area 16 F 31 City On Tuen Mun n 28 a n u Sha Ti Sh n Ti 38 Wai Tsuen Wan West 45 Tsuen05 Wa Tai Wo Ha Che Kung 40 Temple Kwai Hing 07 i 37 Tai Wa Hin Keng 06 l Kwai Fong o n 18 Mei Fo k n g Yi Diamond Hil Kowloon Choi Wa Tsin Tong n i King Wong 25 Shun Ti La Lai Chi Ko Lok Fu d Tai Si Choi Cheung Sha Wan Hung Sau Mau Ping ylan n ay e Sham Shui Po ei Kowloon ak u AsiaWorld-Expo B 46 ShekM T oo Po Tat y Disn Resort m Po Lam Na Kip Kai k 24 Kowl y Sunn eong g Hang Ha Prince n Ba Ch o Sungong 01 53 Airport M Mong W Edward ok ok East 20 K K Toi ong 04 To T Ho Kwa Ngau Tau Ko Cable Car n 23 Olympic Yau Mai Man Wan 44 n a Kwun Ti Ngong Ping 360 19 52 42 n Te Ti 26 Tung Chung East am O 21 L Tung Austi Yau Tong Tseung Chung on Whampo Kwan Tung o n Jordan Tiu g Kowl loo Tsima Hung 51 Ken Chung w Sh Hom Leng West Hong Kong Tsui 32 t Tsim Tsui West Ko Eas 34 22 ha Fortress10 Hill Hong r S ay LOHAS Park ition ew 09 Lantau Island ai Ying Pun Kong b S Tama xhi aus North h 17 11 n E C y o y Centre Ba Nort int 12 16 Po 02 Tai -

Rail Plus Property Development in China: the Pilot Case of Shenzhen
WORKING PAPER RAIL PLUS PROPERTY DEVELOPMENT IN CHINA: THE PILOT CASE OF SHENZHEN LULU XUE, WANLI FANG EXECUTIVE SUMMARY China’s rapid urbanization has increased the demand CONTENTS for both housing and transport, leading to a continuing Executive Summary .......................................1 need for urban transit. Cities face significant challenges 1. Introduction ............................................. 2 in financing the growth of urban transit infrastructure. The current practice of financing urban metro or subway 2. Financing Urban Rail Transit Projects in Chinese projects through municipal fiscal revenues (partly from Cities: The Current Situation ............................. 4 land concession fees) and government-backed bank 3. Implementing R+P in China: Opportunities loans is not only inadequate to meet the demand, but and Challenges ........................................... 6 also exacerbates deep-seated problems like mounting municipal financial liabilities, urban sprawl, and urban 4. Analytical Framework ................................ 10 encroachment on farmland. To address these problems, 5. Shenzhen Case Study ................................ 12 Chinese cities need to diversify the ways in which they 6. Summary and Recommendations ...................29 finance urban metro projects. Appendix............................... ...................... 37 Endnotes 38 In a variety of approaches that aim to alleviate the financ- .................................................. ing problems of local governments, Rail -

Development of High-Speed Rail in the People's Republic of China
ADBI Working Paper Series DEVELOPMENT OF HIGH-SPEED RAIL IN THE PEOPLE’S REPUBLIC OF CHINA Pan Haixiao and Gao Ya No. 959 May 2019 Asian Development Bank Institute Pan Haixiao is a professor at the Department of Urban Planning of Tongji University. Gao Ya is a PhD candidate at the Department of Urban Planning of Tongji University. The views expressed in this paper are the views of the author and do not necessarily reflect the views or policies of ADBI, ADB, its Board of Directors, or the governments they represent. ADBI does not guarantee the accuracy of the data included in this paper and accepts no responsibility for any consequences of their use. Terminology used may not necessarily be consistent with ADB official terms. Working papers are subject to formal revision and correction before they are finalized and considered published. The Working Paper series is a continuation of the formerly named Discussion Paper series; the numbering of the papers continued without interruption or change. ADBI’s working papers reflect initial ideas on a topic and are posted online for discussion. Some working papers may develop into other forms of publication. Suggested citation: Haixiao, P. and G. Ya. 2019. Development of High-Speed Rail in the People’s Republic of China. ADBI Working Paper 959. Tokyo: Asian Development Bank Institute. Available: https://www.adb.org/publications/development-high-speed-rail-prc Please contact the authors for information about this paper. Email: [email protected] Asian Development Bank Institute Kasumigaseki Building, 8th Floor 3-2-5 Kasumigaseki, Chiyoda-ku Tokyo 100-6008, Japan Tel: +81-3-3593-5500 Fax: +81-3-3593-5571 URL: www.adbi.org E-mail: [email protected] © 2019 Asian Development Bank Institute ADBI Working Paper 959 Haixiao and Ya Abstract High-speed rail (HSR) construction is continuing at a rapid pace in the People’s Republic of China (PRC) to improve rail’s competitiveness in the passenger market and facilitate inter-city accessibility. -

China Greater Bay Area Green Infrastructure Investment Opportunities
Green Infrastructure Investment Opportunities THE GUANGDONG-HONG KONG-MACAO GREATER BAY AREA 2021 REPORT Prepared by Climate Bonds Initiative Produced with the kind support of HSBC Executive summary In the Guangdong-Hong Kong-Macao Greater Bay Area (the GBA), which consists of nine cities in Guangdong Province and two special administrative regions, i.e., Hong Kong and Macao, the effects of climate change and the Overall infrastructure Low carbon transport risks associated with a greater than 2°C rise • A total investment of USD135bn was global temperatures by the end of the century • The major infrastructure projects in the planned in rail transit during 14th FYP. are significant due to its high exposure to natural 14th Five-Year-Plan (FYP) of Guangdong hazards and vast coastlines. Province are expected to have a total • A total mileage of about 775 km are investment of RMB5tn (USD776.9bn), of planned in the GBA, the total investment Investment in low carbon solutions will be which green infrastructure investment is about USD72.7bn. essential for mitigating climate risk and meeting is not less than RMB1.9tn (USD299bn), global emission reduction pathways under the • Hong Kong plans to spend around including rail transit, wind power, Paris Climate Change Agreement. The Outline USD3.23bn for four new infrastructure modern water conservancy, ecological Development Plan for the Guangdong-Hong projects which include a railway line. civilization construction and new Kong-Macao Greater Bay Area (the GBA Outline infrastructure construction. Plan) issued by China’s State Council also emphasises green development and ecological • Hong Kong states that the government conservation. -

Business Overview About MTR
Business Overview About MTR MTR is regarded as one of the world’s leading railways for safety, reliability, customer service and cost efficiency. In addition to its Hong Kong, China and international railway operations, the MTR Corporation is involved in a wide range of business activities including the development of residential and commercial properties, property leasing and management, advertising, telecommunication services and international consultancy services. Corporate Strategy MTR is pursuing a new Corporate Strategy, “Transforming the Future”, The MTR Story by more deeply embedding sustainability and Environmental, Social and Governance principles into its businesses and operations The MTR Corporation was established in 1975 as the Mass Transit with the aim of creating more value for all the stakeholders. Railway Corporation with a mission to construct and operate, under prudent commercial principles, an urban metro system to help meet The strategic pillars of the new Corporate Strategy are: Hong Kong’s public transport requirements. The sole shareholder was the Hong Kong Government. The platform columns at To Kwa Wan Station on Tuen Ma Line are decorated with artworks entitled, “Earth Song”, which presents a modern interpretation of the aesthetics of the Song Dynasty, The Company was re-established as the MTR Corporation Limited in June 2000 after the Hong Kong Special Administrative Region illustrating the scenery from day to night and the spring and winter seasons using porcelain clay. Government sold 23% of its issued share capital to private investors Hong Kong Core in an Initial Public Offering. MTR Corporation shares were listed on the Stock Exchange of Hong Kong on 5 October 2000. -

2020 Schedule C (Form 1040) 2020 Page 2 Part III Cost of Goods Sold (See Instructions)
SCHEDULE C Profit or Loss From Business OMB No. 1545-0074 (Form 1040) (Sole Proprietorship) ▶ Go to www.irs.gov/ScheduleC for instructions and the latest information. 2020 Department of the Treasury Attachment Internal Revenue Service (99) ▶ Attach to Form 1040, 1040-SR, 1040-NR, or 1041; partnerships generally must file Form 1065. Sequence No. 09 Name of proprietor Social security number (SSN) A Principal business or profession, including product or service (see instructions) B Enter code from instructions ▶ C Business name. If no separate business name, leave blank. D Employer ID number (EIN) (see instr.) E Business address (including suite or room no.) ▶ City, town or post office, state, and ZIP code F Accounting method: (1) Cash (2) Accrual (3) Other (specify) ▶ G Did you “materially participate” in the operation of this business during 2020? If “No,” see instructions for limit on losses . Yes No H If you started or acquired this business during 2020, check here . ▶ I Did you make any payments in 2020 that would require you to file Form(s) 1099? See instructions . Yes No J If “Yes,” did you or will you file required Form(s) 1099? . Yes No Part I Income 1 Gross receipts or sales. See instructions for line 1 and check the box if this income was reported to you on Form W-2 and the “Statutory employee” box on that form was checked . ▶ 1 2 Returns and allowances . 2 3 Subtract line 2 from line 1 . 3 4 Cost of goods sold (from line 42) . 4 5 Gross profit. Subtract line 4 from line 3 . -

METROS/U-BAHN Worldwide
METROS DER WELT/METROS OF THE WORLD STAND:31.12.2020/STATUS:31.12.2020 ّ :جمهورية مرص العرب ّية/ÄGYPTEN/EGYPT/DSCHUMHŪRIYYAT MISR AL-ʿARABIYYA :القاهرة/CAIRO/AL QAHIRAH ( حلوان)HELWAN-( المرج الجديد)LINE 1:NEW EL-MARG 25.12.2020 https://www.youtube.com/watch?v=jmr5zRlqvHY DAR EL-SALAM-SAAD ZAGHLOUL 11:29 (RECHTES SEITENFENSTER/RIGHT WINDOW!) Altamas Mahmud 06.11.2020 https://www.youtube.com/watch?v=P6xG3hZccyg EL-DEMERDASH-SADAT (LINKES SEITENFENSTER/LEFT WINDOW!) 12:29 Mahmoud Bassam ( المنيب)EL MONIB-( ش ربا)LINE 2:SHUBRA 24.11.2017 https://www.youtube.com/watch?v=-UCJA6bVKQ8 GIZA-FAYSAL (LINKES SEITENFENSTER/LEFT WINDOW!) 02:05 Bassem Nagm ( عتابا)ATTABA-( عدىل منصور)LINE 3:ADLY MANSOUR 21.08.2020 https://www.youtube.com/watch?v=t7m5Z9g39ro EL NOZHA-ADLY MANSOUR (FENSTERBLICKE/WINDOW VIEWS!) 03:49 Hesham Mohamed ALGERIEN/ALGERIA/AL-DSCHUMHŪRĪYA AL-DSCHAZĀ'IRĪYA AD-DĪMŪGRĀTĪYA ASCH- َ /TAGDUDA TAZZAYRIT TAMAGDAYT TAỴERFANT/ الجمهورية الجزائرية الديمقراطيةالشعبية/SCHA'BĪYA ⵜⴰⴳⴷⵓⴷⴰ ⵜⴰⵣⵣⴰⵢⵔⵉⵜ ⵜⴰⵎⴰⴳⴷⴰⵢⵜ ⵜⴰⵖⴻⵔⴼⴰⵏⵜ : /DZAYER TAMANEỴT/ دزاير/DZAYER/مدينة الجزائر/ALGIER/ALGIERS/MADĪNAT AL DSCHAZĀ'IR ⴷⵣⴰⵢⴻⵔ ⵜⴰⵎⴰⵏⴻⵖⵜ PLACE DE MARTYRS-( ع ني نعجة)AÏN NAÂDJA/( مركز الحراش)LINE:EL HARRACH CENTRE ( مكان دي مارت بز) 1 ARGENTINIEN/ARGENTINA/REPÚBLICA ARGENTINA: BUENOS AIRES: LINE:LINEA A:PLACA DE MAYO-SAN PEDRITO(SUBTE) 20.02.2011 https://www.youtube.com/watch?v=jfUmJPEcBd4 PIEDRAS-PLAZA DE MAYO 02:47 Joselitonotion 13.05.2020 https://www.youtube.com/watch?v=4lJAhBo6YlY RIO DE JANEIRO-PUAN 07:27 Así es BUENOS AIRES 4K 04.12.2014 https://www.youtube.com/watch?v=PoUNwMT2DoI