DOCSLIB.ORG

POSTLUDE P.1 Letter Frequencies

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
POSTLUDE P.1 Letter Frequencies POSTLUDE A Prelude opened this textbook with the puzzle Mastermind that introduced combinatorial reasoning in a recreational setting. This Postlude looks at a cryptanalysis problem that is again of a recreational nature but also illustrates the less structured side of combinatorial reasoning as it often occurs in real-world problems. In particular, we will look at a simple cryptographic scheme in which the analysis of underlying combinatorial problems is complicated by the somewhat random pattern of letters in English text. P.1 Letter Frequencies There have been many tables produced of the relative frequencies of letters in English writing, starting with Samuel Morse (of Morse code fame). We use frequencies averaged over several tables. Most Common Letters in English Text Vowels Consonants E 12% T 9% A, I, O 8 % N, R, S 6-8% D, L 4% The least frequent letters, all consonants, are: J, Q, X, Z below .05% As we shall see, it is also useful to know which pairs of consecutive letters, called digraphs, are most frequent. The eight most common digraphs are Most frequent: TH Second most frequent: HE Next six most frequent: ER, RE and AN, EN, IN, ON N is unique among the very frequent letters in that close to 90% of its occurrences are preceded by a vowel; other frequent letters have a much wider range of other letters preceding them. Some other frequent digraphs that can be helpful are: ES, SE ED, DE ST TE, TI, TO OF Frequent consonants tend to appear beside vowels but vowels do not occur side-by-side often and similarly frequent consonants do not appear side-by-side often except for TH and ST. So there is a quasi-bipartite graph-like relationship with vowels as one set of vertices and frequent consonants as the other set of vertices in the bipartition), and the frequent digraphs are the edges. There is one triple of consecutive letters, called a trigraph, that stands out, namely, THE. THE is four times as common as any other trigraph in English text. It is frequent both as a three-letter word and as a part of other words. If we are given an encoded message, we could count the frequency of each letter in the message to determine single-letter frequencies. To get information of how often various letters occur before and after other letters, we build what is called a trigraphic frequency 1 table. For each occurrence of a letter, we record the letter just preceding and the letter following this letter. To illustrate, consider the following cryptogram. Here spaces have been removed between words, but for readability letters are written in groups of five. Cryptogram FJYHP KKYRH YKYRF HYVYK PRQYI SFIFP RNAVP PUDQC CAYJY COQRF JYRYD TQYCO JPMIY FJQIN YSVTP VFJYT QVIFF QKYQR FJYES IFIFM OYRFI JSWYP TFYRK QIAYJ QWYOQ RSVPD ONRPQ INTSI JQPRP MFIQO YQFQI JPEYO FJSFF JYQRO PPVIY FFQRB DQCCA VQRBP MFFJY AYIFQ RFJQI NYSVI BVSOM SFQRB HCSII FJYVY DQCCA YRPOY CQWYV QYIPT OPKQR PIEQX XSSCC PDYOQ RIQOY Table P.1: Trigraph table for cryptogram 6 4 12 6 3 27 0 4 22 16 7 0 5 5 13 21 31 20 13 6 1 12 3 2 37 0 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z NV RD QC UQ YS .J YP YS FY PK PI RA CQ HK RY YH IF DQ PD YY SY QX JH CY RP CA YT PY RH RY FF YY KY FO IY CJ KR DC YF YV VP AP QY XS KR IY IV YO PO IQ SI FY MY FY YY PF OR MY FR OR PQ EI YQ ST QY HK CV RH YO BQ IP BC QN OP YP PF IT YQ VP TY PN JW PF PF KR YY HS QC YQ RJ VF FQ QY OS IY DN PU JI QF RV NS QI HV CY CA PY YJ SF FY RQ QY JM QN YY TI PO SP VK HS VJ FF FY PQ YF TV TV QF JF PI QI QC IF FJ IS RP YT FK YF YV AQ AJ CA FQ QA YQ SM VD YR YK VO SI JC YQ RJ QN IQ PY RQ KI QS MF BS JR SC II SJ IP TP QR JW NP CI YY RD CP IM FQ FS YQ RM OR PP XS YQ QC RI QJ FY QY JE PI QO SC IF TY VF FY OP JP QB NS MI YF FQ PV IO QB JT QQ QN FY BM YF QF KQ OJ VB RO FI QB JE SF SI IT YR YP OR FJ IF OK FR QP WP YF YP RI DC QI FR FQ PE CD VR AJ MF RQ FR WO FJ JI OQ IQ FR EO RJ DC JQ SQ CW IF IJ VY JA KR AI EX NS OR JV IQ VD AR OC WV QI DO O. 2 The trigraphic frequency table for the cryptogram is given in Table P.1. Letter frequencies appear at the top of each column in Table P.1. When a trigraph is repeated in some letter’s column, the trigraph is underlined. To illustrate how the table is constructed, consider the beginning of the cryptogram: FJYHP KKY . For each occurrence of a letter, we enter the letter just before it and the letter just after it. For the first letter is F, we enter .J in F’s column (the ‘.’ indicates that since F is the first letter of the message, no letter precedes it). For the second letter J in the message, we enter FY in J’s column. For the third letter Y, we enter JH in Y’s column. For the fourth letter H, we enter YP in H’s column; for the fifth letter P, we enter HK in P’s column. For the sixth letter K, we enter PK in K’s column. Since the seventh letter is also K, next in K’s column, we enter KY. For the frequent letters, their columns of trigraph data can be overwhelming, and so it is helpful to make a digraph table for each frequent letter, such as F, listing the frequency of letters that occur 2 or more times Before F and After F. See Table P.2. Table P.2: Digraph repetitions for frequent letters in table P.1 12 27 21 16 13 22 31 20 14 12 36 C F I J O P Q R S V Y___ Bef Bef Bef Bef Bef Bef Bef Bef Bef Bef Bef Aft C4 F4 F4 F10 C2 J2 D3 P3 J2 A2 A4 3C Q3 I6 Q5 I3 Q2 G2 F4 Q10 S2 P2 I2 2D Y3 M2 S3 Y2 Y3 P2 I3 Y6 Y2 S3 J8 2F R5 V3 R4 J4 Y3 K3 3I Aft S3 Y3 Aft Aft V2 K2 Aft Aft N2 2J 3A Y2 2P 2P O2 3B 3F Aft O4 2K 4C Aft 4Q 2Q Aft T2 4F 3I 3I Q3 30 2O Aft 6F 3S 4Y 2D V2 4P 3V 2P V2 3Q 4F 3J 8Y 2M Y3 2Q W3 6R 4I 3N 2P 2Y 2S 10J 2Q 2R Aft 3V 5Q 2Y 2T 3C 2V 4I 2O 10R 3Y 2W We shall be referring to the data in Tables P.1 and P.2 repeatedly through this Postlude. Finally, we list the sequences of 3 or more letters that are repeated several times in the message. 7 times: FJY 3 times: DQCCA, RFJ, QRB (also DQCCAY 2 times) Note that longer repeats, such as DQCCA and DQCCAY, can be found by looking at trigraph (3-letter) repeats and concatenating these repeats together. That is, DQCCA is built from the repeated trigraphs of DQC, QCC, and CCA. Observe that this 5-letter sequence is probably a word, since the chances are extremely low that a repeated 5-letter sequence would be formed by a common ending of three different words followed by a common start of three other different words. Now we start the decoding process. We typically begin with the letters in the English word THE. The very frequent trigraph FJY is a perfect fit to be the encoding of THE, since: 3 i) THE is the most frequent trigraph in English text and FJY is the most frequent trigraph in the cryptogram (occurring 7 times); ii) E is the most frequent letter in English text and Y is the most frequent letter in our cryptogram; iii) TH is the most frequent digraph in English text and FJ is the most frequent digraph in the cryptogram (occurring 10 times); and iv) T is one of the most frequent letters in English text and F is one of the most frequent letters in our cryptogram. We write the information about the encoding of THE as TP = FC, HP = JC, EP = YC, where the P subscript stands for Plain text and the C subscript stands for Code text. Once we know that EP = YC, we can look for frequent letters that rarely beside Y, keeping in mind that vowels do not occur side-by-side often. Looking through the digraph information in Figure P.2, we see that YC has no repeated occurrences before or after PC (YC appears before PC once and not at all after PC). So PC is extremely likely to be a vowel. To find another vowel, we can look at frequent code letters that have few occurrences of YC and PC before and after them.
Load more

Recommended publications
  • VSI Openvms C Language Reference Manual
    VSI OpenVMS C Language Reference Manual Document Number: DO-VIBHAA-008 Publication Date: May 2020 This document is the language reference manual for the VSI C language. Revision Update Information: This is a new manual. Operating System and Version: VSI OpenVMS I64 Version 8.4-1H1 VSI OpenVMS Alpha Version 8.4-2L1 Software Version: VSI C Version 7.4-1 for OpenVMS VMS Software, Inc., (VSI) Bolton, Massachusetts, USA C Language Reference Manual Copyright © 2020 VMS Software, Inc. (VSI), Bolton, Massachusetts, USA Legal Notice Confidential computer software. Valid license from VSI required for possession, use or copying. Consistent with FAR 12.211 and 12.212, Commercial Computer Software, Computer Software Documentation, and Technical Data for Commercial Items are licensed to the U.S. Government under vendor's standard commercial license. The information contained herein is subject to change without notice. The only warranties for VSI products and services are set forth in the express warranty statements accompanying such products and services. Nothing herein should be construed as constituting an additional warranty. VSI shall not be liable for technical or editorial errors or omissions contained herein. HPE, HPE Integrity, HPE Alpha, and HPE Proliant are trademarks or registered trademarks of Hewlett Packard Enterprise. Intel, Itanium and IA64 are trademarks or registered trademarks of Intel Corporation or its subsidiaries in the United States and other countries. Java, the coffee cup logo, and all Java based marks are trademarks or registered trademarks of Oracle Corporation in the United States or other countries. Kerberos is a trademark of the Massachusetts Institute of Technology.
    [Show full text]
  • Designing Soft Keyboards for Brahmic Scripts
    Designing Soft Keyboards for Brahmic Scripts Lauren Hinkle Miguel Lezcano Jugal Kalita Colorado College University of Colorado University of Colorado Colorado Springs, CO, USA Colorado Springs, CO, USA Colorado Springs, CO, USA lauren.hinkle [email protected] [email protected] @coloradocollege.edu Abstract Soft keyboards allow a user to input text with and without the use of a physical keyboard. They Despite being spoken by a large percent- are versatile because they allow data to be input age of the world, many Indic languages through mouse clicks on an on-screen keyboard, have escaped research and development in through a touch screen on a computer, cell phone, the realm of text-input. There exist lan- or PDA, or by mapping a virtual keyboard to guages with poor or no support for typ- a standard physical keyboard. With the recent ing. Soft keyboards, because of their ease surge in popularity of touchscreen media such of installation and lack of reliance on spe- as cell phones and computers, well-designed cific hardware, are a promising solution as soft keyboards are becoming more important an input device for many languages. De- everywhere. veloping an acceptable soft keyboard re- For languages that don’t conform well to quires frequency analysis of characters in standard QWERTY based keyboards that order to design a layout that minimizes accompany most computers, soft keyboards are text-input time. This paper proposes us- especially important. Brahmic scripts (Coulmas ing various development techniques, lay- 1990) have more characters and ligatures than fit out variations, and evaluation methods usably on a standard keyboard.
    [Show full text]
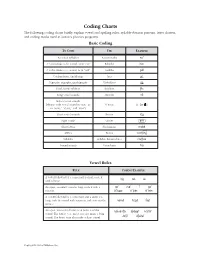
  • Phonics TRB Coding Chart
    Coding Charts The following coding charts briefly explain vowel and spelling rules, syllable-division patterns, letter clusters, and coding marks used in Saxon’s phonics programs. Basic Coding TO CODE USE EXAMPLE Accented syllables Accent marks noÆ C ’s that make a /k/ sound, as in “cat” K-backs |cat C ’s that make a /s/ sound, as in “cell” Cedillas çell Combinations; diphthongs Arcs ar™ Digraphs; trigraphs; quadrigraphs Underlines SH___ Final, stable syllables Brackets [fle Long vowel sounds Macrons nO Schwa vowel sounds (rhymes with vowel sound in “sun,” as Schwas o÷ (or ) in “some,” “about,” and “won”) Short vowel sounds Breves log Sight words Circles ≤are≥ Silent letters Slash marks mak´ Affixes Boxes work ingfl Syllables Syllable division lines cac\tus Voiced sounds Voice lines hiß Vowel Rules RULE CODING EXAMPLE A vowel followed by a consonant is short; code it logcatsit with a breve. An open, accented vowel is long; code it with a nOÆ mEÆ íÆ gOÆ macron. AÆ\|cor™n OÆ\p»n EÆ\v»n A vowel followed by a consonant and a silent e is long; code the vowel with a macron and cross out the nAm´ hOp´ lIk´ silent e. An open, unaccented vowel can make a schwa b«\nanÆ\« E\rAs´Æ hO\telÆ sound. The letters e, o, and u can also make a long sound. The letter i can also make a short sound. JU\lŒÆ di\vId´Æ Copyright by Saxon Publishers, Inc. Spelling Rules† RULE EXAMPLE Floss Rule: When a one-syllable root word has a short vowel sound followed by the sound /f/, /l/, or /s/, it is puff doll pass usually spelled ff, ll, or ss.
    [Show full text]
  • English Literacy Dossier
    English Literacy Dossier Myriam Cherro Samper Javier Fernández Molina Manuel Sánchez Quero 1 ISBN: 978-84-09-19463-6 ENGLISH PHONETICS. INTRODUCTION TO THE SOUNDS OF ENGLISH AND THEIR REPRESENTATION. 1. ENGLISH PHONETICS. INTRODUCTION TO THE SOUNDS OF ENGLISH AND THEIR REPRESENTATION. ... 4 1.1 Definition of Language. ................................................................................................................... 4 1.1.1 Roman Jakobson’s Function of Language Theory .......................................................................... 6 1.2 What Is Linguistics?................................................................................................................................ 7 1.2.1 Linguistic Branches ........................................................................................................................ 8 1.2.2 Phonemes vs. Allophones .............................................................................................................. 8 1.2.3 Phonetics vs. Phonology ................................................................................................................ 9 1.2.4 Minimal Pairs ............................................................................................................................... 10 1.2.5 Homophone vs. Homographs ....................................................................................................... 10 1.3 The English Alphabet. .........................................................................................................................
    [Show full text]
  • Lunyole Grammar; It Does Not Attempt to Make a Statement for Or Against a Particular Formal Linguistic Theory
    A PARTIAL GRAMMAR SKETCH OF LUNYOLE WITH EMPHASIS ON THE APPLICATIVE CONSTRUCTION(S) _______________________ A Thesis Presented to The Faculty of the School of Intercultural Studies Department of Applied Linguistics & TESOL Biola University _______________________ In Partial Fulfillment of the Requirements for the Degree Master of Arts in Applied Linguistics _______________________ by Douglas Allen Wicks May 2006 ABSTRACT A PARTIAL GRAMMAR SKETCH OF LUNYOLE WITH EMPHASIS ON THE APPLICATIVE CONSTRUCTION(S) Douglas Allen Wicks This thesis provides a general grammatical description of Lunyole, a Bantu language of Eastern Uganda. After a brief description of the phonology, it describes the morphology and basic syntax of Lunyole, following Payne’s (1997) functional approach. This thesis then more deeply describes Lunyole’s applicative constructions in which an argument is added to the verb complex. Lunyole has two applicative marking constructions. The more productive one uses the -ir suffix on verbs of any valence in conjunction with a wide range of semantic roles. The other applicative construction is formed from a locative class prefix and is used only for locative arguments on unaccusative intransitive verbs. Similar locative morphemes may co-occur with the -ir applicative morpheme, but not as applicative markers; instead they clarify the relationship between arguments. TABLE OF CONTENTS PAGE List of Tables ..................................................................................................................... ix List of Figures......................................................................................................................x
    [Show full text]
  • How Children Learn to Write Words
    How Children Learn to Write Words How Children Learn to Write Words Rebecca TReiman and bReTT KessleR 1 3 Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford New York Auckland Cape Town Dar es Salaam Hong Kong Karachi Kuala Lumpur Madrid Melbourne Mexico City Nairobi New Delhi Shanghai Taipei Toronto With offices in Argentina Austria Brazil Chile Czech Republic France Greece Guatemala Hungary Italy Japan Poland Portugal Singapore South Korea Switzerland Thailand Turkey Ukraine Vietnam Oxford is a registered trademark of Oxford University Press in the UK and certain other countries. Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016 © Oxford University Press 2014 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by license, or under terms agreed with the appropriate reproduction rights organization. Inquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above. You must not circulate this work in any other form and you must impose this same condition on any acquirer. A copy of this book’s Catalog-in-Publication Data is on file with the Library of Congress ISBN 978–0–19–990797–7
    [Show full text]
  • ADAPTATIONS of HEBREW SCRIPT in This Chapter I Present An
    CHAPTER TWO FROM ARAMEA TO AMERICA: ADAPTATIONS OF HEBREW SCRIPT In this chapter I present an overview of the development of the Hebrew writing system, followed by a survey of language families with attested Hebrew-letter texts. While I aim to provide a broader and more inclusive overview of Hebraicization than has been available previously, I do not make any claim to comprehensiveness. 1. FROM HEBREW TO JEWISH WRITING Nothing is known of Hebraic writing before the Israelites emerged in the land of Canaan and "borrowed the art of writing" from the local inhabitants in the twelfth or eleventh century BCE (Naveh 1982: 65). In the earliest known Hebrew inscription, the Gezer calendar,1 the writing resembles that of tenth-century Phoenician inscriptions from Byblos, and features no specifically Hebrew characters. Indeed, the Phoenician influence was so dominant that neither the Hebrews nor the Aramaeans ever innovated new characters to represent consonant phonemes that did not exist in Phoenician. The first distinctive features of Hebrew writing are actually to be found in ninth-century inscriptions in Moabite, a Canaanite dialect related to Hebrew. According to Naveh (1982), these adaptations of the contemporary Hebrew script represent the first stage of the Hebrew scribal tradition. Despite dialectal differences between the spoken Hebrew of Judah (the 1 Naveh notes that although the calendar can be dated to the late tenth century, the language of this inscription "does not have any lexical or grammatical features that preclude the possibility of its being Phoenician" (1982: 76). southern kingdom) and Israel (the northern kingdom), the same script was used in both kingdoms, as well as by the Moabites and Edomites to write their own kindred languages while under the rule of Israel and Judah.
    [Show full text]
  • Structured Word Inquiry: Developing Literacy and Critical Thinking by Scientific Inquiry About How Spelling Works 1
    Structured Word Inquiry: Developing literacy and critical thinking by scientific inquiry about how spelling works 1 Structured Word Inquiry (Scientific Word Investigation) The Joy of Understanding Spelling struct + ure/ + ed → structured in + struct + ion → instruction Peter Bowers, PhD Instruction which builds understanding of WordWorks Literacy Centre, word structure as a tool for investigating 2020 the interrelation of spelling and meaning. www.WordWorksKingston.com Structured Word Inquiry: Developing literacy and critical thinking by scientific inquiry about how spelling works 2 Guides and some basic terms for Structured Word Inquiry A model of English orthography from Real Spelling Guiding Principles of Structured Word Inquiry The primary function of English spelling is to represent meaning. The conventions by which English spelling represents meaning are so well-ordered and reliable that spelling can be investigated and understood through scientific Explore the Real Spelling Tool Box 2 (on-line) for a remarkable linguistic inquiry. reference to study English orthography. Explore the “Morphology Scientific inquiry is necessary to safely guide spelling Album” in the archive of videos learn more about these and many other instruction and understanding. terms and concepts. The film on “Connecting Vowel Letters” is a Scientific inquiry is the only means by which a particularly rich way to make sense of this term that is absent most learning community can safely accept or reject teacher resources. This newly available reference is one you
    [Show full text]
  • The New Polish Cyrillic in Independent Belarus
    https://doi.org/10.11649/ch.2019.006 Colloquia Humanistica 8 (2019) Hierarchies and Boundaries. Structuring the Social in Eastern Europe and the Mediterranean COLLOQUIA HUMANISTICA Tomasz Kamusella School of History University of St Andrews St Andrews https://orcid.org/0000-0003-3484-8352 [email protected] The New Polish Cyrillic in Independent Belarus Abstract Aer the fall of communism and the breakup of the Soviet Union, the religious life of the Roman Catholic community revived in independent Belarus. e country’s Catholics are concentrated in western Belarus, which prior to World War II was part of Poland. In 1991 in Hrodna (Horadnia, Grodno) Region, the Diocese of Hrodna was established. Slightly over half of the region’s population are Catholics and many identify as ethnic Poles. Following the ban on the ocial use of Polish in postwar Soviet Belarus, the aforementioned region’s population gained an education in Belarusian and Russian, as channeled through the Cyrillic alphabet. Hence, following the 1991 independence of Belarus, the population’s knowledge of the Latin alphabet was none, or minimal. For the sake of providing the faithful with Polish-language religious material that would be of some practical use, the diocesan authorities decided to publish some Polish-language prayer books, but printed in the Russian-style Cyrillic. is currently widespread use of Cyrillic-based Polish-language publications in Belarus remains unknown outside the country, either in Poland or elsewhere in Europe. Keywords: Belarusian language, Cyrillic, Latin alphabet, Diocese of Hrodna (Horadnia, Grodno), nationalism, Polish language, religion, politics of script, Russian language.
    [Show full text]
  • J32. Journal of the Simplified Spelling
    Journal of the Simplified Spelling Society J32, 2003/1. Editor: Steve Bett. Contents. 1. Editorial. Articles. 2. The Two Stage Approach to Spelling Reform. Steve Bett. 3. English Accents and their Implications for Spelling Reform. John C. Wells. 4. How Phonemic is English Spelling? Godfrey Dewey. 5. Could English spelling be made regular without drastic change? Valerie Yule. 6. Orthographic Goals. Steve Bett. 7. Comparing Spelling Schemes. Roy W. Blain. 8. Reform of Chemical Language as a Model for Spelling Reform. Hans-Richard Sliwka. 9. The End of the Reading Wars? Isobel Raven. 10. Review of Jean Meron's Orthotypographie. John M. Gledhill. 11. Letters & Summaries of On-Line Discussions. 12. A Message from the new president: John Wells. 13. Tribute to Don Scragg on his retirement as the Society's president. 14. Inside front cover. We spell a spoken sound in as many as 20 different ways. [Journal of the Simplified Spelling Society, J32, 2003/1, pp2,3 in the printed version.] [Steve Bett: see Journals, Newsletters] 1. Editorial. Steve Bett. Moving from logographic lexical spelling to phonemic spelling. The proposals of the Simplified Spelling Board of 1906 and the Simplified Spelling Society of 1908 were attempts to seek out the lines of least resistance to spelling change. Earlier phonemic spelling associations were thought to advocate reform proposals that were too radical for any popular acceptance. The first compromise, suggested by Alexander Ellis, was to retain the shifted long vowels. In England, this led to the endorsement of New Spelling which became the house style for most internal publications of the society until around 1920.
    [Show full text]
  • A Grammar of Pite Saami
    A grammar of Pite Saami Joshua Wilbur language Studies in Diversity Linguistics, No 5 science press A grammar of Pite Saami Pite Saami is a highly endangered Western Saami language in the Uralic language family currently spoken by a few individuals in Swedish Lapland. This grammar is the first extensive book-length treatment of a Saamilan- guage written in English. While focussing on the morphophonology of the main word classes nouns, adjectives and verbs, it also deals with other linguistic structures such as prosody, phonology, phrase types and clauses. Furthermore, it provides an introduction to the language and its speakers, and an outline of a preliminary Pite Saami orthography. An extensive an- notated spoken-language corpus collected over the course of five years forms the empirical foundation for this description, and each example in- cludes a specific reference to the corpus in order to facilitate verification of claims made on the data. Descriptions are presented for a general lin- guistics audience and without attempting to support a specific theoretical approach. This book should be equally useful for scholars of Uralic linguis- tics, typologists, and even learners of Pite Saami. ISBN 978-3-944675-47-3 Joshua Wilbur A grammar of Pite Saami Studies in Diversity Linguistics Chief Editor: Martin Haspelmath Consulting Editors: Fernando Zúñiga, Peter Arkadiev, Ruth Singer, Pilar Valen zuela In this series: 1. Handschuh, Corinna. A typology of marked-S languages 2. Rießler, Michael. Adjective attribution 3. Klamer, Marian (ed.). The Alor-Pantar languages: History and typology 4. Berghäll, Liisa. A grammar of Mauwake (Papua New Guinea) 5.
    [Show full text]
  • The Dynamics of Bilingual Adult Literacy in Africa: a Case Study of Kom, Cameroon
    The Dynamics of Bilingual Adult Literacy in Africa: A Case Study of Kom, Cameroon Jean Seraphin Kamdem THESIS SUBMITTED FOR THE DEGREE OF DOCTOR OF PHILOSOPHY School of Oriental and African Studies, University of London. 2010 ProQuest Number: 11015877 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 11015877 Published by ProQuest LLC(2018). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 DECLARATION OF OWNERSHIP I, the undersigned, hereby declare that the work presented in this thesis is my own work and has not been written for me in whole or part by any other person. Signed: J. S. Kamdem 2 | SOA Q lARY ABSTRACT This thesis investigates, describes and analyses adult literacy in local languages in Africa, with a focus on Kom, a rural community situated in the North West province of Cameroon. The thesis presents the motivations, relevance, importance and aims of the research; then gives an overview of the national and local backgrounds, namely Cameroon and Kom. A detailed description is given of the multilingual landscape and language use in formal education, the development of writing systems for Cameroonian languages, the official literacy activities at the national level, and the Kom language and community.
    [Show full text]