DOCSLIB.ORG

THE INDEX of DISPERSION by EDGAR G. AVELINO B.Sc, The

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
THE INDEX of DISPERSION by EDGAR G. AVELINO B.Sc, The THE INDEX OF DISPERSION By EDGAR G. AVELINO B.Sc, The University of British Columbia, 1978 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FQR THE DEGREE OF MASTER OF SCIENCE in THE FACULTY OF GRADUATE STUDIES , Statistics Department The University of British Columbia We accept this thesis as conforming to the_ requifibd/t stan'cQrd' THE UNIVERSITY OF BRITISH COLUMBIA November 1934 © Edgar G. Avelino, 1984 In presenting this thesis in partial fulfilment of the requirements for an advanced degree at the University of British Columbia, I agree that the Library shall make it freely available for reference and study. I further agree that permission for extensive copying of this thesis for scholarly purposes may be granted by the head of my department or by his or her representatives. It is understood that copying or publication of this thesis for financial gain shall not be allowed without my written permission. Department of GTA7~/S7?&' The University of British Columbia 1956 Main Mall Vancouver, Canada V6T 1Y3 Date 'OCT- A3, /<?8y DE-6 (3/81) i i ABSTRACT The index of dispersion is a statistic commonly used to detect departures from randomness of count data. Under the hypothesis of randomness, the true distribution of this statistic is unknown. The accu• racy of large sample approximations is assessed by a Monte Carlo simulation. Further approximations by Pearson curves and infinite series expansions are in• vestigated. Finally, the powers of the individual tests based on the likelihood ratio, the index of dis• persion and Pearson's goodness-of-fit statistic are compared. i i i TABLE OF CONTENTS PAGE ABSTRACT ii ACKNOWLEDGEMENT ix 1. INTRODUCTION 1.1 History of the Index of Dispersion 1 1.2 Purpose of the Paper 4 2. LARGE SAMPLE APPROXIMATIONS 2.1 Joint Distribution of X & S2 6 2.2 The Asymptotic Distribution of I 7 2.3 Description of the Monte Carlo Simulation 9 2.4 The x2 Approximation 14 2.5 Discussion 15 3. PEARSON CURVES 3.1 The Theory of Pearson Curves 19 3.2 Two Examples 21 3.3 The First Four Moments of I 24 3.4 Discussion 29 iv PAGE 4. THE GRAM-CHARLIER SERIES OF TYPE A 4.1 The Theory of Gram-Charlier Expansions 37 4.2 Discussion 42 5. THE LIKELIHOOD RATIO AND GOODNESS-OF-FIT TESTS 5.1 The Likelihood Ratio Test 49 5.2 Pearson's Goodness-of-Fit Test 54 5.3 Power Computations 55 5.4 The Likelihood Ratio Test Revisited 65 6. GONGLUSIONS 74 REFERENCES .....76 APPENDIX Al.l The Conditional Distribution of a Poisson Sample Given the Total 79 A1.2 The First Four Moments of I 80 A1.3 The Type VI Pearson Curve 87 A1.4 A Limiting Case of the Negative Binomial 88 A2.1 Histograms of I 90 A2.2 Empirical Critical Values 106 A2.3 Pearson Curve Critical Values 107 A2.4 Gram-Charlier Critical Values 109 V TABLE OF CONTENTS LIST OF TABLES PAGE TABLE 1: Expected Number of I*'s 10 TABLE 2 (A-D): Normal Approximation 11 2 TABLE 3 (A-D): x Approximation 16 TABLE 4 (A-D): Pearson Curve Fit with Exact Moments 31 TABLE 5 (A-D): Pearson Curve Fit with Asymptotic Moments 33 TABLE 6 (A-D): Gram-Charlier Three-Moment Fit (Exact) 43 TABLE 7 (A-D): Gram-Charlier Four-Moment Fit (Exact) 45 TABLE 8: Asymptotic Power of the Index of Dispersion Test -. 57 TABLE 9-10 (A-D): Power of Tests Based on A,I and X2 60 TABLE 11 (A-D): Power of Tests Based on A and I (n=50).. 66 TABLE 12: Number of Times (n-l)S2 ^ nX 68 TABLE 13 (A-B): Power of Tests Based on A,I and X2 (n=10) 70 TABLE 14 (A-B): Power of Tests Based on A,I and X2 (n=20) 71 vi PAGE TABLE 15 (A-B): Power of Tests Based on A and I (n=50).. 72 2 TABLE Al: The Ratios of the Moments of I and x n_! 86 TABLE A2: Emperical Critical Values of I (Based on 15,000 Samples) 106 TABLE A3: Pearson Curve Critical Values (Exact) 107 TABLE A4: Pearson Curve Critical Values (Asymptotic) 108 TABLE A5: Gram-Charlier Critical Values (Three Exact Moments) 109 TABLE A6: Gram-Charlier Critical Values (Three Asymptotic Moments) 110 TABLE A7: Gram-Charlier Critical Values (Four Exact Moments) Ill TABLE A8: Gram-Charlier Critical Values (Four Asymptotic Moments) 112 vii TABLE OF CONTENTS LIST OF FIGURES PAGE FIG. A.l: Histogram of I (1000 Samples, n = 10, X = 3) 90 FIG. A.2: Histogram of I (1000 Samples, n = 10, X = 5) 91 FIG. A.3: Histogram of I (1000 Samples, n = 20, X = 3) 92 FIG. A.4: Histogram of I (1000 Samples, n = 20, X = 5) 93 FIG. A.5: Histogram of I (1000 Samples, n = 50, X = 3) 94 FIG. A.6: Histogram of I (1000 Samples, n = 50, X = 5) 95 FIG. A.7: Histogram of I (1000 Samples, n = 100, X = 3) 96 FIG. A.8: Histogram of I (1000 Samples, n = 100, X = 5) 97 FIG. A.9: Normal Probability Plot for I (1000 Samples, n = 10, X = 3) 9S v i i i PAGE FIG. A.10: Normal Probability Plot for I (1000 Samples, n = 10, x = 5) 9S FIG. A.11: Normal Probability Plot for I (1000 Samples, n = 20, x = 3) 100 FIG. A.12: Normal Probability 'Plot for I (1000 Samples, n = 20, x = 5) 101 FIG. A.13: Normal Probability Plot for I (1000 Samples, n = 50, X = 3) 102 FIG. A.14: Normal Probability Plot for I (1000 Samples, n = 50, X = 5) 103 FIG. Ail5: Normal Probability Plot for I (1000 Samples, n =.100, X = 3) 104 FIG. A.16: Normal Probability Plot for I (1000 Samples, n = 100, X = 5) 105 ix ACKNOWLEDGEMENT I wish to express my sincere appreciation to Prof. A. John Petkau who devoted precious time to the supervision of this thesis. Edgar G. Avelino 1 1. INTRODUCTION 1.1 HISTORY OF THE INDEX OF DISPERSION The index of dispersion is a test statistic often used to detect spatial pattern, a term ecologists use to describe non-randomness of plant populations. This is equivalent to testing that the growth of plants over an area is purely random, or equivalently that the number of plants in any given area has the Poisson distribution. Suppose then that we randomly partition some area by n disjoint equal-sized quadrats and make a count, x, of the number of plants in each quadrat. Under the hypothesis of randomness, Xj, ... , Xnwould have the Poisson distribution, P(X=x) = e'V/xl , for x > 0 and x = 0, 1, 2, ... , for which E(X) = Var(X) = X. For alternatives to complete randomness involving patches or clumping of plants, we would expect Var(X) > E(X), while for more regular spacing of plants, we would expect Var(X) < E(X) (see for example R.H. Green (1966)) . These properties lead quite naturally to considering the variance-to-mean ratio as a population index to measure spatial pattern. An estimator of the variance-to-mean ratio is the index of dispersion, defined as 1 , if I = 0 I = I s2/x if X > 0 n n where X = (1/n) F. X. and S2 = {l/(n-l)> z (X.-X)2, the i=l 1 i=l 1 2 unbiased estimators of E(X) and Var(X), respectively. (It is natural to define I to be 1 if X = 0 because under the null hypothesis, the variance-to-mean ratio equals 1.) Ever since G.E. Blackman (1935) used the Poisson model for counts of plants, the concept of randomness in a community of plants became a growing interest among ecologists. Although the index of dispersion was introduced by R.A. Fisher (Fisher, Thornton and MacKenzie, 1922), it was not until 1936 that it was first used by ecologists for the purpose of inference. A.R. Clapham (1936), using a x2 approximation for the distribution of the index of dispersion under the null hypothesis of randomness, found that among 44 plant species he studied, only four of these seemed to be distributed randomly, while over-dispersion (i.e. clumping) was clearly present for the remaining species. Student (1919) had already pointed out that the Poisson is not usually a good model for ecological data and in most cases, clumping occurs. This has been termed "contagious" by G. Polya (1930) and also by J. Neyman (1939). Ever since Clapham's paper, the use of the index of dispersion as a test of significance of departures from randomness has been extensive, not just for field data, but also in other areas (for example, blood counts, insect counts and larvae counts). Fisher et al (1922) showed that the distribution of the index of dispersion could be closely approximated by the x2 distribution with n-1 degrees of freedom. However, if the Poisson parameter, X» is small, or if the estimated expectation, X, is smal1, then the adequacy of the 3 x2 approximation becomes questionable. This is discussed by H.O. Lancaster (1952). Fisher (1950) and W.G. Cochran (1936) have pointed out that in this case, the test of randomness based on I should be done conditionally with given totals, £X.j. Since this sum is a sufficient statistic for the Poisson parameter X, conditioning on the total will yield a distribution independent of X. Hence, exact frequencies can be computed. The conditional moments of the index of dispersion are provided in Appendix A1.2.
Load more

Recommended publications
  • A Two Parameter Discrete Lindley Distribution
    Revista Colombiana de Estadística January 2016, Volume 39, Issue 1, pp. 45 to 61 DOI: http://dx.doi.org/10.15446/rce.v39n1.55138 A Two Parameter Discrete Lindley Distribution Distribución Lindley de dos parámetros Tassaddaq Hussain1;a, Muhammad Aslam2;b, Munir Ahmad3;c 1Department of Statistics, Government Postgraduate College, Rawalakot, Pakistan 2Department of Statistics, Faculty of Sciences, King Abdulaziz University, Jeddah, Saudi Arabia 3National College of Business Administration and Economics, Lahore, Pakistan Abstract In this article we have proposed and discussed a two parameter discrete Lindley distribution. The derivation of this new model is based on a two step methodology i.e. mixing then discretizing, and can be viewed as a new generalization of geometric distribution. The proposed model has proved itself as the least loss of information model when applied to a number of data sets (in an over and under dispersed structure). The competing mod- els such as Poisson, Negative binomial, Generalized Poisson and discrete gamma distributions are the well known standard discrete distributions. Its Lifetime classification, kurtosis, skewness, ascending and descending factorial moments as well as its recurrence relations, negative moments, parameters estimation via maximum likelihood method, characterization and discretized bi-variate case are presented. Key words: Characterization, Discretized version, Estimation, Geometric distribution, Mean residual life, Mixture, Negative moments. Resumen En este artículo propusimos y discutimos la distribución Lindley de dos parámetros. La obtención de este Nuevo modelo está basada en una metodo- logía en dos etapas: mezclar y luego discretizar, y puede ser vista como una generalización de una distribución geométrica. El modelo propuesto de- mostró tener la menor pérdida de información al ser aplicado a un cierto número de bases de datos (con estructuras de supra y sobredispersión).
    [Show full text]
  • Descriptive Statistics
    IMGD 2905 Descriptive Statistics Chapter 3 Summarizing Data Q: how to summarize numbers? • With lots of playtesting, there is a lot of data (good!) • But raw data is often just a pile of numbers • Rarely of interest, or even sensible Summarizing Data Measures of central tendency Groupwork 4 3 7 8 3 4 22 3 5 3 2 3 • Indicate central tendency with one number? • What are pros and cons of each? Measure of Central Tendency: Mean • Aka: “arithmetic mean” or “average” =AVERAGE(range) =AVERAGEIF() – averages if numbers meet certain condition Measure of Central Tendency: Median • Sort values low to high and take middle value =MEDIAN(range) Measure of Central Tendency: Mode • Number which occurs most frequently • Not too useful in many cases Best use for categorical data • e.g., most popular Hero group in http://pad3.whstatic.com/images/thumb/c/cd/Find-the-Mode-of-a-Set-of-Numbers- Heroes of theStep-7.jpg/aid130521-v4-728px-Find-the-Mode-of-a-Set-of-Numbers-Step-7.jpg Storm =MODE() Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? mean median modes mode mean median frequency no mode mean (a) median (b) frequency mode mode median median (c) mean mean frequency frequency frequency (d) (e) Which to Use: Mean, Median, Mode? Which to Use: Mean, Median, Mode? • Mean many statistical tests that use sample ‒ Estimator of population mean ‒ Uses all data Which to Use: Mean, Median, Mode? • Median is useful for skewed data ‒ e.g., income data (US Census) or housing prices (Zillo) ‒ e.g., Overwatch team (6 players): 5 people level 5, 1 person level 275 ₊ Mean is 50 - not so useful since no one at this level ₊ Median is 5 – perhaps more representative ‒ Does not use all data.
    [Show full text]
  • The Need to Measure Variance in Experiential Learning and a New Statistic to Do So
    Developments in Business Simulation & Experiential Learning, Volume 26, 1999 THE NEED TO MEASURE VARIANCE IN EXPERIENTIAL LEARNING AND A NEW STATISTIC TO DO SO John R. Dickinson, University of Windsor James W. Gentry, University of Nebraska-Lincoln ABSTRACT concern should be given to the learning process rather than performance outcomes. The measurement of variation of qualitative or categorical variables serves a variety of essential We contend that insight into process can be gained purposes in simulation gaming: de- via examination of within-student and across-student scribing/summarizing participants’ decisions for variance in decision-making. For example, if the evaluation and feedback, describing/summarizing role of an experiential exercise is to foster trial-and- simulation results toward the same ends, and error learning, the variance in a student’s decisions explaining variation for basic research purposes. will be greatest when the trial-and-error stage is at Extant measures of dispersion are not well known. its peak. To the extent that the exercise works as Too, simulation gaming situations are peculiar in intended, greater variances would be expected early that the total number of observations available-- in the game play as opposed to later, barring the usually the number of decision periods or the game world encountering a discontinuity. number of participants--is often small. Each extant measure of dispersion has its own limitations. On the other hand, it is possible that decisions may Common limitations are that, under ordinary be more consistent early and then more variable later circumstances and especially with small numbers if the student is trying to recover from early of observations, a measure may not be defined and missteps.
    [Show full text]
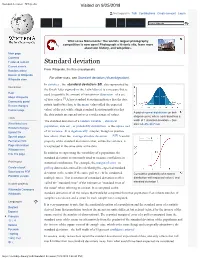
  • Standard Deviation - Wikipedia Visited on 9/25/2018
    Standard deviation - Wikipedia Visited on 9/25/2018 Not logged in Talk Contributions Create account Log in Article Talk Read Edit View history Wiki Loves Monuments: The world's largest photography competition is now open! Photograph a historic site, learn more about our history, and win prizes. Main page Contents Featured content Standard deviation Current events Random article From Wikipedia, the free encyclopedia Donate to Wikipedia For other uses, see Standard deviation (disambiguation). Wikipedia store In statistics , the standard deviation (SD, also represented by Interaction the Greek letter sigma σ or the Latin letter s) is a measure that is Help used to quantify the amount of variation or dispersion of a set About Wikipedia of data values.[1] A low standard deviation indicates that the data Community portal Recent changes points tend to be close to the mean (also called the expected Contact page value) of the set, while a high standard deviation indicates that A plot of normal distribution (or bell- the data points are spread out over a wider range of values. shaped curve) where each band has a Tools The standard deviation of a random variable , statistical width of 1 standard deviation – See What links here also: 68–95–99.7 rule population, data set , or probability distribution is the square root Related changes Upload file of its variance . It is algebraically simpler, though in practice [2][3] Special pages less robust , than the average absolute deviation . A useful Permanent link property of the standard deviation is that, unlike the variance, it Page information is expressed in the same units as the data.
    [Show full text]
  • Population Dispersion
    AccessScience from McGraw-Hill Education Page 1 of 7 www.accessscience.com Population dispersion Contributed by: Francis C. Evans Publication year: 2014 The spatial distribution at any particular moment of the individuals of a species of plant or animal. Under natural conditions organisms are distributed either by active movements, or migrations, or by passive transport by wind, water, or other organisms. The act or process of dissemination is usually termed dispersal, while the resulting pattern of distribution is best referred to as dispersion. Dispersion is a basic characteristic of populations, controlling various features of their structure and organization. It determines population density, that is, the number of individuals per unit of area, or volume, and its reciprocal relationship, mean area, or the average area per individual. It also determines the frequency, or chance of encountering one or more individuals of the population in a particular sample unit of area, or volume. The ecologist therefore studies not only the fluctuations in numbers of individuals in a population but also the changes in their distribution in space. See also: POPULATION DISPERSAL. Principal types of dispersion The dispersion pattern of individuals in a population may conform to any one of several broad types, such as random, uniform, or contagious (clumped). Any pattern is relative to the space being examined; a population may appear clumped when a large area is considered, but may prove to be distributed at random with respect to a much smaller area. Random or haphazard. This implies that the individuals have been distributed by chance. In such a distribution, the probability of finding an individual at any point in the area is the same for all points (Fig.
    [Show full text]
  • Summarizing Measured Data
    SummarizingSummarizing MeasuredMeasured DataData Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 [email protected] These slides are available on-line at: http://www.cse.wustl.edu/~jain/cse567-08/ Washington University in St. Louis CSE567M ©2008 Raj Jain 12-1 OverviewOverview ! Basic Probability and Statistics Concepts: CDF, PDF, PMF, Mean, Variance, CoV, Normal Distribution ! Summarizing Data by a Single Number: Mean, Median, and Mode, Arithmetic, Geometric, Harmonic Means ! Mean of A Ratio ! Summarizing Variability: Range, Variance, percentiles, Quartiles ! Determining Distribution of Data: Quantile-Quantile plots Washington University in St. Louis CSE567M ©2008 Raj Jain 12-2 PartPart III:III: ProbabilityProbability TheoryTheory andand StatisticsStatistics 1. How to report the performance as a single number? Is specifying the mean the correct way? 2. How to report the variability of measured quantities? What are the alternatives to variance and when are they appropriate? 3. How to interpret the variability? How much confidence can you put on data with a large variability? 4. How many measurements are required to get a desired level of statistical confidence? 5. How to summarize the results of several different workloads on a single computer system? 6. How to compare two or more computer systems using several different workloads? Is comparing the mean sufficient? 7. What model best describes the relationship between two variables? Also, how good is the model? Washington University in St. Louis CSE567M ©2008 Raj Jain 12-3 BasicBasic ProbabilityProbability andand StatisticsStatistics ConceptsConcepts ! Independent Events: Two events are called independent if the occurrence of one event does not in any way affect the probability of the other event.
    [Show full text]
  • Swedish Translation for the ISI Multilingual Glossary of Statistical Terms, Prepared by Jan Enger, Bernhard Huitfeldt, Ulf Jorner, and Jan Wretman
    Swedish translation for the ISI Multilingual Glossary of Statistical Terms, prepared by Jan Enger, Bernhard Huitfeldt, Ulf Jorner, and Jan Wretman. Finally revised version, January 2008. For principles, see the appendix.
    [Show full text]
  • A Modified Conway-Maxwell-Poisson Type Binomial Distribution and Its
    A modified Conway–Maxwell–Poisson type binomial distribution and its applications T. Imotoa, C. M. Ngb, S. H. Ongb and S. Chakrabortyc a School of Management and Information, University of Shizuoka, 51-1 Yada, Suruga-ku, Shuzuoka 422-8526, Japan b Institute of Mathematical Sciences, Faculty of Science, University of Malaya, 50603 Kuala Lumpur, Malaysia c Department of Statistics, Dibrugarh University, Dibrugarh-786004, Assam, India Corresponding author E-mail: [email protected] Key Words: dispersion; exponential family; kurtosis; modality; queueing process; skewness. Abstract This paper proposes a generalized binomial distribution with four parameters, which is derived from the finite capacity queueing system with state-dependent service and arrival rates. This distribution is also generated from the conditional Conway–Maxwell– Poisson distribution given a sum of two Conway–Maxwell–Poisson variables. In this paper, we consider the properties about the probability mass function, index of dispersion, skew- ness and kurtosis and give applications of the proposed distribution from its geneses. The estimation method and simulation study are also considered. 1. Introduction The binomial distribution is classically utilized as a model for analyzing count data with finite support since it has a simple genesis arising from Bernoulli trials and belongs to the exponential family that can model under-dispersion, in which the variance is smaller than the mean. However, its reliance on the simple genesis limits its flexibility in many applications. arXiv:1610.05232v1 [math.ST] 17 Oct 2016 For examples, the binomial distribution cannot model over-dispersion, lepto-kurtosis when the mode is around n/2 and platy-kurtosis when the mode is around 0 or n, where n is an integer parameter of the binomial distribution.
    [Show full text]
  • Exponential Dispersion Models for Overdispersed Zero-Inflated Count
    Exponential Dispersion Models for Overdispersed Zero-Inflated Count Data Shaul K. Bar-Leva Ad Ridderb aFaculty of Tech. Man., Holon Institute of Technology, Holon, Israel, [email protected] bDepartment of EOR, VU University, Amsterdam, Netherlands, [email protected] April 1, 2020 Abstract We consider three new classes of exponential dispersion models of discrete probability dis- tributions which are defined by specifying their variance functions in their mean value parame- terization. In a previous paper (Bar-Lev and Ridder, 2020a), we have developed the framework of these classes and proved that they have some desirable properties. Each of these classes was shown to be overdispersed and zero inflated in ascending order, making them as competitive statistical models for those in use in statistical modeling. In this paper we elaborate on the computational aspects of their probability mass functions. Furthermore, we apply these classes for fitting real data sets having overdispersed and zero-inflated statistics. Classic models based on Poisson or negative binomial distributions show poor fits, and therefore many alternatives have already proposed in recent years. We execute an extensive comparison with these other proposals, from which we may conclude that our framework is a flexible tool that gives excellent results in all cases. Moreover, in most cases our model gives the best fit. Keywords: Count distributions, Exponential dispersion models, Overdispersion, Zero-inflated models, Fit models 1 Introduction In many scientific fields, one deals with systems, experiments, or phenomena that have random arXiv:2003.13854v1 [stat.ME] 30 Mar 2020 discrete outcomes. These outcomes are revealed typically through a set of data obtained by ob- serving the system and counting the occurrences.
    [Show full text]
  • Nematic Van Der Waals Free Energy
    Available Online JOURNAL OF SCIENTIFIC RESEARCH Publications J. Sci. Res. 11 (1), 1-13 (2019) www.banglajol.info/index.php/JSR On Poisson-Weighted Lindley Distribution and Its Applications R. Shanker, K. K. Shukla* Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea Received 26 May 2018, accepted in final revised form 18 July 2018 Abstract In this paper the nature and behavior of its coefficient of variation, skewness, kurtosis and index of dispersion of Poisson- weighted Lindley distribution (P-WLD), a Poisson mixture of weighted Lindley distribution, have been proposed and the nature and behavior have been explained graphically. Maximum likelihood estimation has been discussed to estimate its parameters. Applications of the proposed distribution have been discussed and its goodness of fit has been compared with Poisson distribution (PD), Poisson-Lindley distribution (PLD), negative binomial distribution (NBD) and generalized Poisson-Lindley distribution (GPLD). Keywords: Poisson lindley distribution; Weighted lindley distribution, Compounding; Skewness; Kurtosis; Maximum likelihood estimation. © 2019 JSR Publications. ISSN: 2070-0237 (Print); 2070-0245 (Online). All rights reserved. doi: http://dx.doi.org/10.3329/jsr.v11i1.35745 J. Sci. Res. 11 (1), 1-13 (2019) 1. Introduction M. Shankaran [1] proposed the Poisson-Lindley distribution (PLD) to model count data defined by its probability mass function (pmf) 2 x 2 (1.1) P1 x; ; x 0,1,2,..., 0 1x3 Shanker and Hagos [2] proposed a simple method of finding moments of PLD and discussed the applications of PLD to model count data from biological sciences. Shanker and Shukla [3] proposed a generalized size-biased Lindley distribution which includes size-biased Poisson-Lindley distribution introduced by Ghitany et al.
    [Show full text]
  • On the Distribution Theory of Over-Dispersion Evdokia Xekalaki
    Xekalaki Journal of Statistical Distributions and Applications 2014, 1:19 http://www.jsdajournal.com/content/1/1/19 REVIEW Open Access On the distribution theory of over-dispersion Evdokia Xekalaki Correspondence: [email protected] Department of Statistics, Athens Abstract University of Economics and Business, 76 Patision St., Athens, An overview of the evolution of probability models for over-dispersion is given Greece looking at their origins, motivation, first main contributions, important milestones and applications. A specific class of models called the Waring and generalized Waring models will be a focal point. Their advantages relative to other classes of models and how they can be adapted to handle multivariate data and temporally evolving data will be highlighted. Keywords: Heterogeneity; Contagion; Clustering; Spells model; Accident proneness; Mixtures; Zero-adjusted models; Biased sampling; Generalized Waring distribution; Generalized Waring process 1. Introduction Data analysts have often to deal with data that exhibit a variability that differs from what they expect on the basis of the hypothesized model. The phenomenon is known as overdispersion if the observed variability exceeds the expected variability or under- dispersion if it is lower than expected. Such differences between observed and nominal variances can be interpreted as brought about by failures of some of the basic assumptions of the model. These can be classified by the mechanism leading to them. As summarized by Xekalaki (2006), in traditional experimental contexts, they may be caused by deviations from the hypothe- sized structure of the population, due to lack of independence between individual item responses, contagion, clustering, and heterogeneity. In observational study contexts, on the other hand, they are the result of the method of ascertainment, which can lead to partial distortion of the observations.
    [Show full text]
  • Akash Distribution, Compounding, Moments, Skewness, Kurtosis, Estimation of Parameter, Statistical Properties, Goodness of Fit
    International Journal of Probability and Statistics 2017, 6(1): 1-10 DOI: 10.5923/j.ijps.20170601.01 The Discrete Poisson-Akash Distribution Rama Shanker Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea Abstract A Poisson-Akash distribution has been obtained by compounding Poisson distribution with Akash distribution introduced by Shanker (2015). A general expression for the r th factorial moment has been derived and hence the first four moments about origin and the moments about mean has been obtained. The expressions for its coefficient of variation, skewness and kurtosis have been obtained. Its statistical properties including generating function, increasing hazard rate and unimodality and over-dispersion have been discussed. The maximum likelihood estimation and the method of moments for estimating its parameter have been discussed. The goodness of fit of the proposed distribution using maximum likelihood estimation has been given for some count data-sets and the fit is compared with that obtained by other distributions. Keywords Akash distribution, Compounding, Moments, Skewness, Kurtosis, Estimation of parameter, Statistical properties, Goodness of fit lifetime data from engineering and medical science and 1. Introduction concluded that Akash distribution has some advantage over Lindley and exponential distributions, Lindley distribution A lifetime distribution named, “Akash distribution” has some advantage over Akash and exponential having probability density function distributions and exponential distribution
    [Show full text]