DOCSLIB.ORG

Measuring Wage Dispersion: Pay Ranges Reflect Industry Traits

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measuring Wage Dispersion: Pay Ranges Reflect Industry Traits Measuring wage dispersion: pay ranges reflect industry traits Greatest wage dispersion occurs in industries with broad occupational stafung or with much incentive pay; high paying industries, often heavily unionized, show less variation in earnings and a penchant for single job rates CARL B. BARSKY AND MARTIN E. PERSONICK Wage rates in an industry can vary a great deal above The data reveal substantial differences in the degree and below the average wage for that industry. However, of wage dispersion among various industries, apparently in another industry with a similar average wage, the governed by two competing groups of factors: (1) range of pay rates can be small. What causes such dif- companywide bargaining and single job rates create low ferent wage dispersions among industries? Using meas- wage dispersion in industries such as glass containers ures of relative dispersion, this analysis shows that in- and cigarettes; and (2) broad occupational staffing pat- dustry characteristics such as degree of unionization, terns and incentive pay systems tend to produce large geographic location, occupational mix, and method of wage spreads in industries such as meat products and wage payment influence the amount of variation. Recent men's suits. In general, high-paying industries, often wage data for a cross-section of manufacturing and highly unionized, show less variation in individual earn- mining industries are examined in this article. ings than low-paying industries . Differences in pay lev- The Bureau's Industry Wage Survey program is espe- els among establishments are a dominant characteristic cially suited to analysis of wage dispersion. Individual of industries with widely dispersed earnings. surveys provide straight-time hourly earnings data for a Employee opportunities for increased pay take dif- number of detailed occupations representing an indus- ferent forms that are related to the degree of industry try's wage structure. Information is recorded on each wage dispersion. Uniformity of wages, as found in many establishment's location, collective bargaining status, high-paying industries, might discourage movement of and number of employees, as well as on its major prod- workers between firms (that may pay the same rates set uct and production processes. In addition, sex and by union agreement). However, widely dispersed earn- method of wage payment are recorded for individual ings, often in low-paying industries, may encourage workers. workers to seek increased earnings through shifts to Data for 43 manufacturing and six mining industries higher paying firms or to those using incentive pay sys- surveyed during 1973-78 are used in this analysis .' tems. These narrowly defined industries, although not a prob- In addition to individual workers, others who make ability sample of all industries, adequately represent the decisions based on wage rate distributions include com- many kinds of manufacturing and mining activities in panies who set their wage levels at stipulated distances the United States . from an industry or area-wide average, market research- ers testing the Carl B . Barsky is an economist and Martin E. Personick a project di- potential demand for new consumer rector in the Division of Occupational Wage Structures, Bureau of La- products, and tax analysts estimating revenues from bor Statistics . workers at different earnings levels. 35 MONTHLY LABOR REVIEW April 1981 e Measuring Wage Dispersion devia- Analytical technique workers fall within plus or minus one standard tion of the mean . In this analysis of wage dispersion, two basic for the cen- Before defining the dispersion measures in this analy- approaches are used : the spread in earnings is related to sis, let us look at a full earnings distribution to find tral portion of the industry's distribution dispersion ; and the some of its kcv points. Chart 1 describes the wage dis- the median value by the index of distribution about the tribution in basic steel, which corresponds closely to a variation of all wage rates in the of variation. "bell-shaped" curve; in fact, its mean and median value mean value is summarized by the coefficient by dividing the are exactly the same . Moreover, its first and third quar- The index of dispersion is computed between the third and tiles- the points above and below which a fourth of the interquartile range (the difference quartile) and mul- workers fall - are each about equidistant from the me- first quartiles) by the median (second basic steel, it is dian . The standard deviation can be thought of as the tiplying by 100 . In the case of the distribution of average distance (dispersion) of workers' earnings from $1 .46i$8 .32 X 100 = 18. Obviously, of the array has no the industry's mean . Typically, about two-thirds of the rates at the upper and lower fourth Chart 1 . Distribution of hourly earnings of production workers in basic iron and steel, February 1978 Percent o workers 20 18 16 Mean and median 14 12 10 4 0 60 4 40 5 20 6_00 680 7 I 40 9 2C 0 .00 10 80 1 1 60 1,' 40 Earnings 36 influence on the index values. Further, the actual wage mum wage when the surveys were last conducted . The rates other than the three quartiles do not affect the dis- median-based dispersion index suggests that these in- persion index; this measure is determined only by the dustries have as much relative dispersion as, for exam- position of these quartiles, and not the shape of the dis- ple, meatpacking-an industry which is not influenced tribution within the band. The median standardizes the by the minimum wage and which has one of the highest index of dispersion, so that a distribution of relatively coefficients of variation (29) among those reported . high rates may be compared with one of low rates. For At the other end of the earnings array, the lead and example, if one industry has quartiles of $4 .00, $4 .50, zinc mining industry has some "hidden" dispersion in and .00, $5 and a second has quartiles of $8 .00, $8 .50, the upper one-fourth of its earnings distribution . Min- and $9.00, both would have an interquartile range of ers, primarily paid on an incentive basis, had earnings $1 .00. The indexes of dispersion are 22 for the first in- that were usually scattered throughout that upper por- dustry and 12 in the second, indicating more relative tion. As a result, the industry's dispersion index value dispersion in the lower paying industry . of 18 ranks relatively low (although second highest The coefficient of variation is computed by dividing among the mining segment); but, its coefficient of varia- the standard deviation by the mean and multiplying by tion (26) is among the upper third of those reported. 100. The calculation for basic steel would be $1 .25 Rankings of the coefficients of variation were com- $8.32 100 = X 15. As with the dispersion index, a cen- pared with rankings of such characteristics as industry tral value-the mean-is used to standardize the earn- pay level, unionization, and the use of single-rate pay ings dispersion for situations with varying pay levels. systems . Based on Spearman rank correlation tests, the Most of the analysis in this article relies on the degree of dispersion is inversely related to these factors .' coefficient of variation as a measure of dispersion. Us- Table 2 portrays the inverse relationship found be- ing either the dispersion index or the coefficient of vari- tween dispersion and pay levels for 28 industries. Only ation, however, will generally result in similar con- the meatpacking and motor vehicle parts industries clusions when comparing wage dispersion among in- were in the top third of rankings of both industry pay dustries or other economic units.z (See "technical note" levels and dispersion, and none of the industries fell that follows for a comparison of how the two measures into the bottom third of both categories. Consistent may differ .) The primary advantage of the coefficient of with the Spearman test, a clustering occurred for indus- variation approach is that total variation in earnings tries with the highest pay levels and the lowest coeffi- around the mean can be measured and then, broken cients of variation. into two component parts-earnings variations among Industries with low dispersion rates were, as and within establishments . expected, highly unionized . There were, however, other highly unionized industries with broadly Ranking wage spreads dispersed earn- ings-such as men's suits, leather tanning, and gray Two sets of dispersion rates by industry are shown in iron (except pipe and fittings) foundries . The latter in- table 1 . Indexes of dispersion were, with few exceptions, dustries had substantial proportions of workers under higher than coefficients of variation, but both measures incentive pay plans. Four industries with coefficients of yielded similar rankings of industries based on Spear- variation of 10 or less (underground coal, iron and cop- man tests.' Industries with the least degree of earnings per mining, and petroleum refining), in addition to be- variation included motor vehicle manufacturing, several ing virtually 100 percent unionized, were marked by mining groups, petroleum refining, and cellulosic fibers. almost complete mechanization of production processes The most dispersed earnings were reported in semicon- and, therefore, a virtual absence of worker control over ductors and men's suit and coat manufacturing . output . As a result, time rates are paid almost exclus- In certain instances, the two dispersion measures ively in these industries, producing low wage dispersion . were dissimilar in rank or value. The coefficients of vari- Industries with high dispersion rates were invariably ation for the women's hosiery and men's and boy's those using pay plans other than single-rate systems. shirts industries, for example, were 21 and 22, respec- Men's suits, with the second highest coefficient of varia- tively, indicating a moderate amount of dispersion .
Load more

Recommended publications
  • A Two Parameter Discrete Lindley Distribution
    Revista Colombiana de Estadística January 2016, Volume 39, Issue 1, pp. 45 to 61 DOI: http://dx.doi.org/10.15446/rce.v39n1.55138 A Two Parameter Discrete Lindley Distribution Distribución Lindley de dos parámetros Tassaddaq Hussain1;a, Muhammad Aslam2;b, Munir Ahmad3;c 1Department of Statistics, Government Postgraduate College, Rawalakot, Pakistan 2Department of Statistics, Faculty of Sciences, King Abdulaziz University, Jeddah, Saudi Arabia 3National College of Business Administration and Economics, Lahore, Pakistan Abstract In this article we have proposed and discussed a two parameter discrete Lindley distribution. The derivation of this new model is based on a two step methodology i.e. mixing then discretizing, and can be viewed as a new generalization of geometric distribution. The proposed model has proved itself as the least loss of information model when applied to a number of data sets (in an over and under dispersed structure). The competing mod- els such as Poisson, Negative binomial, Generalized Poisson and discrete gamma distributions are the well known standard discrete distributions. Its Lifetime classification, kurtosis, skewness, ascending and descending factorial moments as well as its recurrence relations, negative moments, parameters estimation via maximum likelihood method, characterization and discretized bi-variate case are presented. Key words: Characterization, Discretized version, Estimation, Geometric distribution, Mean residual life, Mixture, Negative moments. Resumen En este artículo propusimos y discutimos la distribución Lindley de dos parámetros. La obtención de este Nuevo modelo está basada en una metodo- logía en dos etapas: mezclar y luego discretizar, y puede ser vista como una generalización de una distribución geométrica. El modelo propuesto de- mostró tener la menor pérdida de información al ser aplicado a un cierto número de bases de datos (con estructuras de supra y sobredispersión).
    [Show full text]
  • Descriptive Statistics
    IMGD 2905 Descriptive Statistics Chapter 3 Summarizing Data Q: how to summarize numbers? • With lots of playtesting, there is a lot of data (good!) • But raw data is often just a pile of numbers • Rarely of interest, or even sensible Summarizing Data Measures of central tendency Groupwork 4 3 7 8 3 4 22 3 5 3 2 3 • Indicate central tendency with one number? • What are pros and cons of each? Measure of Central Tendency: Mean • Aka: “arithmetic mean” or “average” =AVERAGE(range) =AVERAGEIF() – averages if numbers meet certain condition Measure of Central Tendency: Median • Sort values low to high and take middle value =MEDIAN(range) Measure of Central Tendency: Mode • Number which occurs most frequently • Not too useful in many cases Best use for categorical data • e.g., most popular Hero group in http://pad3.whstatic.com/images/thumb/c/cd/Find-the-Mode-of-a-Set-of-Numbers- Heroes of theStep-7.jpg/aid130521-v4-728px-Find-the-Mode-of-a-Set-of-Numbers-Step-7.jpg Storm =MODE() Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? frequency Mean, Median, Mode? mean median modes mode mean median frequency no mode mean (a) median (b) frequency mode mode median median (c) mean mean frequency frequency frequency (d) (e) Which to Use: Mean, Median, Mode? Which to Use: Mean, Median, Mode? • Mean many statistical tests that use sample ‒ Estimator of population mean ‒ Uses all data Which to Use: Mean, Median, Mode? • Median is useful for skewed data ‒ e.g., income data (US Census) or housing prices (Zillo) ‒ e.g., Overwatch team (6 players): 5 people level 5, 1 person level 275 ₊ Mean is 50 - not so useful since no one at this level ₊ Median is 5 – perhaps more representative ‒ Does not use all data.
    [Show full text]
  • The Need to Measure Variance in Experiential Learning and a New Statistic to Do So
    Developments in Business Simulation & Experiential Learning, Volume 26, 1999 THE NEED TO MEASURE VARIANCE IN EXPERIENTIAL LEARNING AND A NEW STATISTIC TO DO SO John R. Dickinson, University of Windsor James W. Gentry, University of Nebraska-Lincoln ABSTRACT concern should be given to the learning process rather than performance outcomes. The measurement of variation of qualitative or categorical variables serves a variety of essential We contend that insight into process can be gained purposes in simulation gaming: de- via examination of within-student and across-student scribing/summarizing participants’ decisions for variance in decision-making. For example, if the evaluation and feedback, describing/summarizing role of an experiential exercise is to foster trial-and- simulation results toward the same ends, and error learning, the variance in a student’s decisions explaining variation for basic research purposes. will be greatest when the trial-and-error stage is at Extant measures of dispersion are not well known. its peak. To the extent that the exercise works as Too, simulation gaming situations are peculiar in intended, greater variances would be expected early that the total number of observations available-- in the game play as opposed to later, barring the usually the number of decision periods or the game world encountering a discontinuity. number of participants--is often small. Each extant measure of dispersion has its own limitations. On the other hand, it is possible that decisions may Common limitations are that, under ordinary be more consistent early and then more variable later circumstances and especially with small numbers if the student is trying to recover from early of observations, a measure may not be defined and missteps.
    [Show full text]
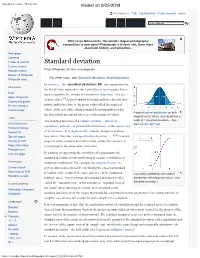
  • Standard Deviation - Wikipedia Visited on 9/25/2018
    Standard deviation - Wikipedia Visited on 9/25/2018 Not logged in Talk Contributions Create account Log in Article Talk Read Edit View history Wiki Loves Monuments: The world's largest photography competition is now open! Photograph a historic site, learn more about our history, and win prizes. Main page Contents Featured content Standard deviation Current events Random article From Wikipedia, the free encyclopedia Donate to Wikipedia For other uses, see Standard deviation (disambiguation). Wikipedia store In statistics , the standard deviation (SD, also represented by Interaction the Greek letter sigma σ or the Latin letter s) is a measure that is Help used to quantify the amount of variation or dispersion of a set About Wikipedia of data values.[1] A low standard deviation indicates that the data Community portal Recent changes points tend to be close to the mean (also called the expected Contact page value) of the set, while a high standard deviation indicates that A plot of normal distribution (or bell- the data points are spread out over a wider range of values. shaped curve) where each band has a Tools The standard deviation of a random variable , statistical width of 1 standard deviation – See What links here also: 68–95–99.7 rule population, data set , or probability distribution is the square root Related changes Upload file of its variance . It is algebraically simpler, though in practice [2][3] Special pages less robust , than the average absolute deviation . A useful Permanent link property of the standard deviation is that, unlike the variance, it Page information is expressed in the same units as the data.
    [Show full text]
  • Population Dispersion
    AccessScience from McGraw-Hill Education Page 1 of 7 www.accessscience.com Population dispersion Contributed by: Francis C. Evans Publication year: 2014 The spatial distribution at any particular moment of the individuals of a species of plant or animal. Under natural conditions organisms are distributed either by active movements, or migrations, or by passive transport by wind, water, or other organisms. The act or process of dissemination is usually termed dispersal, while the resulting pattern of distribution is best referred to as dispersion. Dispersion is a basic characteristic of populations, controlling various features of their structure and organization. It determines population density, that is, the number of individuals per unit of area, or volume, and its reciprocal relationship, mean area, or the average area per individual. It also determines the frequency, or chance of encountering one or more individuals of the population in a particular sample unit of area, or volume. The ecologist therefore studies not only the fluctuations in numbers of individuals in a population but also the changes in their distribution in space. See also: POPULATION DISPERSAL. Principal types of dispersion The dispersion pattern of individuals in a population may conform to any one of several broad types, such as random, uniform, or contagious (clumped). Any pattern is relative to the space being examined; a population may appear clumped when a large area is considered, but may prove to be distributed at random with respect to a much smaller area. Random or haphazard. This implies that the individuals have been distributed by chance. In such a distribution, the probability of finding an individual at any point in the area is the same for all points (Fig.
    [Show full text]
  • Summarizing Measured Data
    SummarizingSummarizing MeasuredMeasured DataData Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 [email protected] These slides are available on-line at: http://www.cse.wustl.edu/~jain/cse567-08/ Washington University in St. Louis CSE567M ©2008 Raj Jain 12-1 OverviewOverview ! Basic Probability and Statistics Concepts: CDF, PDF, PMF, Mean, Variance, CoV, Normal Distribution ! Summarizing Data by a Single Number: Mean, Median, and Mode, Arithmetic, Geometric, Harmonic Means ! Mean of A Ratio ! Summarizing Variability: Range, Variance, percentiles, Quartiles ! Determining Distribution of Data: Quantile-Quantile plots Washington University in St. Louis CSE567M ©2008 Raj Jain 12-2 PartPart III:III: ProbabilityProbability TheoryTheory andand StatisticsStatistics 1. How to report the performance as a single number? Is specifying the mean the correct way? 2. How to report the variability of measured quantities? What are the alternatives to variance and when are they appropriate? 3. How to interpret the variability? How much confidence can you put on data with a large variability? 4. How many measurements are required to get a desired level of statistical confidence? 5. How to summarize the results of several different workloads on a single computer system? 6. How to compare two or more computer systems using several different workloads? Is comparing the mean sufficient? 7. What model best describes the relationship between two variables? Also, how good is the model? Washington University in St. Louis CSE567M ©2008 Raj Jain 12-3 BasicBasic ProbabilityProbability andand StatisticsStatistics ConceptsConcepts ! Independent Events: Two events are called independent if the occurrence of one event does not in any way affect the probability of the other event.
    [Show full text]
  • Swedish Translation for the ISI Multilingual Glossary of Statistical Terms, Prepared by Jan Enger, Bernhard Huitfeldt, Ulf Jorner, and Jan Wretman
    Swedish translation for the ISI Multilingual Glossary of Statistical Terms, prepared by Jan Enger, Bernhard Huitfeldt, Ulf Jorner, and Jan Wretman. Finally revised version, January 2008. For principles, see the appendix.
    [Show full text]
  • A Modified Conway-Maxwell-Poisson Type Binomial Distribution and Its
    A modified Conway–Maxwell–Poisson type binomial distribution and its applications T. Imotoa, C. M. Ngb, S. H. Ongb and S. Chakrabortyc a School of Management and Information, University of Shizuoka, 51-1 Yada, Suruga-ku, Shuzuoka 422-8526, Japan b Institute of Mathematical Sciences, Faculty of Science, University of Malaya, 50603 Kuala Lumpur, Malaysia c Department of Statistics, Dibrugarh University, Dibrugarh-786004, Assam, India Corresponding author E-mail: [email protected] Key Words: dispersion; exponential family; kurtosis; modality; queueing process; skewness. Abstract This paper proposes a generalized binomial distribution with four parameters, which is derived from the finite capacity queueing system with state-dependent service and arrival rates. This distribution is also generated from the conditional Conway–Maxwell– Poisson distribution given a sum of two Conway–Maxwell–Poisson variables. In this paper, we consider the properties about the probability mass function, index of dispersion, skew- ness and kurtosis and give applications of the proposed distribution from its geneses. The estimation method and simulation study are also considered. 1. Introduction The binomial distribution is classically utilized as a model for analyzing count data with finite support since it has a simple genesis arising from Bernoulli trials and belongs to the exponential family that can model under-dispersion, in which the variance is smaller than the mean. However, its reliance on the simple genesis limits its flexibility in many applications. arXiv:1610.05232v1 [math.ST] 17 Oct 2016 For examples, the binomial distribution cannot model over-dispersion, lepto-kurtosis when the mode is around n/2 and platy-kurtosis when the mode is around 0 or n, where n is an integer parameter of the binomial distribution.
    [Show full text]
  • Exponential Dispersion Models for Overdispersed Zero-Inflated Count
    Exponential Dispersion Models for Overdispersed Zero-Inflated Count Data Shaul K. Bar-Leva Ad Ridderb aFaculty of Tech. Man., Holon Institute of Technology, Holon, Israel, [email protected] bDepartment of EOR, VU University, Amsterdam, Netherlands, [email protected] April 1, 2020 Abstract We consider three new classes of exponential dispersion models of discrete probability dis- tributions which are defined by specifying their variance functions in their mean value parame- terization. In a previous paper (Bar-Lev and Ridder, 2020a), we have developed the framework of these classes and proved that they have some desirable properties. Each of these classes was shown to be overdispersed and zero inflated in ascending order, making them as competitive statistical models for those in use in statistical modeling. In this paper we elaborate on the computational aspects of their probability mass functions. Furthermore, we apply these classes for fitting real data sets having overdispersed and zero-inflated statistics. Classic models based on Poisson or negative binomial distributions show poor fits, and therefore many alternatives have already proposed in recent years. We execute an extensive comparison with these other proposals, from which we may conclude that our framework is a flexible tool that gives excellent results in all cases. Moreover, in most cases our model gives the best fit. Keywords: Count distributions, Exponential dispersion models, Overdispersion, Zero-inflated models, Fit models 1 Introduction In many scientific fields, one deals with systems, experiments, or phenomena that have random arXiv:2003.13854v1 [stat.ME] 30 Mar 2020 discrete outcomes. These outcomes are revealed typically through a set of data obtained by ob- serving the system and counting the occurrences.
    [Show full text]
  • Nematic Van Der Waals Free Energy
    Available Online JOURNAL OF SCIENTIFIC RESEARCH Publications J. Sci. Res. 11 (1), 1-13 (2019) www.banglajol.info/index.php/JSR On Poisson-Weighted Lindley Distribution and Its Applications R. Shanker, K. K. Shukla* Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea Received 26 May 2018, accepted in final revised form 18 July 2018 Abstract In this paper the nature and behavior of its coefficient of variation, skewness, kurtosis and index of dispersion of Poisson- weighted Lindley distribution (P-WLD), a Poisson mixture of weighted Lindley distribution, have been proposed and the nature and behavior have been explained graphically. Maximum likelihood estimation has been discussed to estimate its parameters. Applications of the proposed distribution have been discussed and its goodness of fit has been compared with Poisson distribution (PD), Poisson-Lindley distribution (PLD), negative binomial distribution (NBD) and generalized Poisson-Lindley distribution (GPLD). Keywords: Poisson lindley distribution; Weighted lindley distribution, Compounding; Skewness; Kurtosis; Maximum likelihood estimation. © 2019 JSR Publications. ISSN: 2070-0237 (Print); 2070-0245 (Online). All rights reserved. doi: http://dx.doi.org/10.3329/jsr.v11i1.35745 J. Sci. Res. 11 (1), 1-13 (2019) 1. Introduction M. Shankaran [1] proposed the Poisson-Lindley distribution (PLD) to model count data defined by its probability mass function (pmf) 2 x 2 (1.1) P1 x; ; x 0,1,2,..., 0 1x3 Shanker and Hagos [2] proposed a simple method of finding moments of PLD and discussed the applications of PLD to model count data from biological sciences. Shanker and Shukla [3] proposed a generalized size-biased Lindley distribution which includes size-biased Poisson-Lindley distribution introduced by Ghitany et al.
    [Show full text]
  • On the Distribution Theory of Over-Dispersion Evdokia Xekalaki
    Xekalaki Journal of Statistical Distributions and Applications 2014, 1:19 http://www.jsdajournal.com/content/1/1/19 REVIEW Open Access On the distribution theory of over-dispersion Evdokia Xekalaki Correspondence: [email protected] Department of Statistics, Athens Abstract University of Economics and Business, 76 Patision St., Athens, An overview of the evolution of probability models for over-dispersion is given Greece looking at their origins, motivation, first main contributions, important milestones and applications. A specific class of models called the Waring and generalized Waring models will be a focal point. Their advantages relative to other classes of models and how they can be adapted to handle multivariate data and temporally evolving data will be highlighted. Keywords: Heterogeneity; Contagion; Clustering; Spells model; Accident proneness; Mixtures; Zero-adjusted models; Biased sampling; Generalized Waring distribution; Generalized Waring process 1. Introduction Data analysts have often to deal with data that exhibit a variability that differs from what they expect on the basis of the hypothesized model. The phenomenon is known as overdispersion if the observed variability exceeds the expected variability or under- dispersion if it is lower than expected. Such differences between observed and nominal variances can be interpreted as brought about by failures of some of the basic assumptions of the model. These can be classified by the mechanism leading to them. As summarized by Xekalaki (2006), in traditional experimental contexts, they may be caused by deviations from the hypothe- sized structure of the population, due to lack of independence between individual item responses, contagion, clustering, and heterogeneity. In observational study contexts, on the other hand, they are the result of the method of ascertainment, which can lead to partial distortion of the observations.
    [Show full text]
  • Akash Distribution, Compounding, Moments, Skewness, Kurtosis, Estimation of Parameter, Statistical Properties, Goodness of Fit
    International Journal of Probability and Statistics 2017, 6(1): 1-10 DOI: 10.5923/j.ijps.20170601.01 The Discrete Poisson-Akash Distribution Rama Shanker Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea Abstract A Poisson-Akash distribution has been obtained by compounding Poisson distribution with Akash distribution introduced by Shanker (2015). A general expression for the r th factorial moment has been derived and hence the first four moments about origin and the moments about mean has been obtained. The expressions for its coefficient of variation, skewness and kurtosis have been obtained. Its statistical properties including generating function, increasing hazard rate and unimodality and over-dispersion have been discussed. The maximum likelihood estimation and the method of moments for estimating its parameter have been discussed. The goodness of fit of the proposed distribution using maximum likelihood estimation has been given for some count data-sets and the fit is compared with that obtained by other distributions. Keywords Akash distribution, Compounding, Moments, Skewness, Kurtosis, Estimation of parameter, Statistical properties, Goodness of fit lifetime data from engineering and medical science and 1. Introduction concluded that Akash distribution has some advantage over Lindley and exponential distributions, Lindley distribution A lifetime distribution named, “Akash distribution” has some advantage over Akash and exponential having probability density function distributions and exponential distribution
    [Show full text]