DOCSLIB.ORG

Experiment 2 Simple Lenses Introduction Focal Lengths of Simple Lenses 1. Positive Lens

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Experiment 2 Simple Lenses Introduction Focal Lengths of Simple Lenses 1. Positive Lens Experiment 2 Simple Lenses Introduction In this experiment you will measure the focal lengths of (1) a simple positive lens and (2) a simple negative lens. In each case, you will be given a specific method of measurement, and be told how to calculate the focal length from this measurement. Material on thin lenses can be found in J. &W. 4.1 - 4.9, 4.14, 4.15 and P. &P. 3-9, 3-10, and 3-11. Focal Lengths of Simple Lenses There are six sections in this lab. In each section you will measure the focal length of a simple lens. 1. Positive Lens Procedure For the first section, you will make several measurements of image and object distances for a simple positive focal length lens (f = +20 cm). Place an illuminated object at one end of the optical bench. Then place the positive lens 60 cm from the object. Place a large white screen on the other end of the bench and move it toward the lens until you find the image. Record both the object distance and the image distance. Move the screen a few centimeters away and then find the image position again. Take total of five measurements of the image distance. Repeat the above steps for an object distance of 30 centimeters. Make only one careful measurement of the image distance for object distances of 55, 50, 40, 45, and 35 cm. You will continue to move the lens toward the object but now the images will become virtual, since you will be moving inside the focal length of the lens. Since you can no longer use the screen to find the image, you must locate the image by an alternative method. Here, you will employ a device called a range finder. The operation of the range finder will be explained in lab. The range finder should be located 20 cm from the simple lens (see Figure 2 and 3). Replace the illuminated object with the white screen. Note that the screen has a black line on the back. This line will be the new object. Place the lens 16cm from the object. Figure 1: Positive Lens, Real Image Figure 2: Positive Lens, Virtual Image Measure the image distance. Remember the range finder will tell you the distance of the image from the range finder, you must subtract the distance of the range finder from the lens in order to find the image distance. Take a total of five measurements of the image distance. Repeat the above steps for an object distance of 8 cm. Make only one careful measurement of the image distance for object distances of 14, 12 and 10 cm. Analysis In order to find the focal length of the lens from these data, the simple-minded approach would be to use the lens equation, compute several values for the focal length and average. This is not what you are going to do. Instead, you will plot the data and find the focal length from the intercepts. Plot the values of (1/u) vs. (1/v). The intercepts of this graph will be (1/f). Of course there are two intercepts that can be used. Compute f from both these intercepts. Be sure to estimate the error in the intercepts using a least squares fit. Then from the error in the intercepts calculate the errors in the focal length. If you need help with this, see your instructor. See the Report Outline for additional instructions. 2. Negative Lens Procedure In the second section you will repeat Section 1, but you will use a negative lens (f = -20cm) instead of a positive lens. Make five measurements of the image distance for object distances of 55, 35, and 15 cm. Then make only one measurement with object distances of 50, 45, 40, 30, 25, 20 cm. You will note that a negative lens always produces a virtual image, so you will need to use the range finder to measure all of the image distances in this section. Figure 3: Negative Lens Analysis The method for computing the focal length is the same as Section 1. However, you will note that in this case you are computing the focal length by extrapolation, while in Section 1 you're using interpolation. Do you see any difference in accuracy? 3. Spherometer Procedure In this section you will use the spherometer to measure the focal length of both lenses. Actually you will measure the radius of curvature, and using an assumed value for the refractive index of glass, calculate the focal length. Figure 4: Spherometer Measure the distance from the center of the spherometer to one of the legs. You can measure the distance r with a simple scale. Place the spherometer on a plane mirror and record the reading. This reading on the micrometer corresponds to zero curvature. Place the spherometer on each lens and record the reading. (This is a special case. You only need one careful measurement here. We have found that repeating the measurement many times would only give the same result many times. There are no averages to be taken in this section.) Also note that you only need to measure one side of each lens. You will assume that they are symmetric. (they are indeed close). Analysis Now from your readings you can calculate the focal length using the lens makers formula. The radius of curvature can be calculated using, 2 For a symmetric lens, R1 = -R2, so the lens makers formula is just, 1 21 where h is the difference between the spherometer reading for flat glass and the spherometer reading for the lens. r is the distance from the center of the spherometer to each leg. The refractive index, n, is assumed to be 1.517. Compute the error in your result by using the standard propagation of error method. In other words, given the precision of measurement of h and r, compute the error in R and the compute the error in f. A side note here, the percent error in R is the same as the percent error in f. That might help a little. 4. Object at ∞ Procedure This is the quick and dirty method of getting the focal length of a positive lens. Figure 5: Object at ∞ Place the image on the optical bench and place a large white screen behind the lens. Form an image of the far wall on the screen. Record the image distance. Repeat this measurement five times. It is best here to let each lab partner take a couple of measurements independently to reduce systematic error. Record the distance from the lens to the wall which you are using for an object. This is not used to get the focal length (you are assuming the object is at ∞). This measurement is for the error analysis only. Analysis Since you assume that the distance to the wall is infinite, the image distance equals the focal length . Compute the average image distance, the standard deviation, and the standard deviation of the mean. Compare the average focal length to the more exact value obtained by using the finite distance to the wall. How big is the error caused by assuming that the object distance is infinite? 5. Autocollimation Procedure The autocollimation method allows us to place an object exactly in the focal plane of a lens. This means that light from the object will be parallel (collimated) when it emerges from the lens. Figure 6: Autocollimation Place the illuminated object at one end of the bench. Place the positive lens about 20 cm from the object. Now place the large plane mirror behind the lens. Rotate the mirror until you can see that the light from the object is reflected back on itself. Move the lens back and forth until you get a sharp focus. There is a trick to this: place a piece of white paper next to the object so that you can see an image on the paper. The distance from the object to the lens is the focal length. Repeat this measurement five times. After you have taken your fifth data point, remove the large mirror. You should now have an object which is in effect infinitely far away. Place a 10cm lens on the bench and a screen behind it. Focus the image of the object on the screen. Check to see if indeed the image distance is 10cm. Analysis Compute the average as in Section 4. 6. Two Position Method Procedure This method will be used again in later experiments. Be sure that you understand the principles involved and keep this procedure available for future reference. Figure 7: Two Position Method Place the illuminated object at one end of the optical bench. Place the screen 100cm from the object on the other end of the bench. Place the positive lens about 20cm from the object. Move the lens away from the object until you get a sharp image on the screen. Record the position of the lens on the bench. Move the lens away from the object until you get the other image. Again record the position of the lens. Now the difference in bench readings is the distance d. Repeat this five times. Do not move the screen or the object. Measure the distance from the object to the screen with a metric tape. This is the distance L. Analysis Using the formula /4, compute five values of the focal length and average. Addendum The range finder can be used to measure distances with the following formula: Where Range = distance from the range finder objective lens to the object R∞ = reading for an object at infinity R = reading for the distance you are measuring f = focal length of the range finder objective lens i = Dir - Range where Dir= the distance between the simple lens and the Range finder objective .
Load more

Recommended publications
  • Panoramas Shoot with the Camera Positioned Vertically As This Will Give the Photo Merging Software More Wriggle-Room in Merging the Images
    P a n o r a m a s What is a Panorama? A panoramic photo covers a larger field of view than a “normal” photograph. In general if the aspect ratio is 2 to 1 or greater then it’s classified as a panoramic photo. This sample is about 3 times wider than tall, an aspect ratio of 3 to 1. What is a Panorama? A panorama is not limited to horizontal shots only. Vertical images are also an option. How is a Panorama Made? Panoramic photos are created by taking a series of overlapping photos and merging them together using software. Why Not Just Crop a Photo? • Making a panorama by cropping deletes a lot of data from the image. • That’s not a problem if you are just going to view it in a small format or at a low resolution. • However, if you want to print the image in a large format the loss of data will limit the size and quality that can be made. Get a Really Wide Angle Lens? • A wide-angle lens still may not be wide enough to capture the whole scene in a single shot. Sometime you just can’t get back far enough. • Photos taken with a wide-angle lens can exhibit undesirable lens distortion. • Lens cost, an auto focus 14mm f/2.8 lens can set you back $1,800 plus. What Lens to Use? • A standard lens works very well for taking panoramic photos. • You get minimal lens distortion, resulting in more realistic panoramic photos. • Choose a lens or focal length on a zoom lens of between 35mm and 80mm.
    [Show full text]
  • Chapter 3 (Aberrations)
    Chapter 3 Aberrations 3.1 Introduction In Chap. 2 we discussed the image-forming characteristics of optical systems, but we limited our consideration to an infinitesimal thread- like region about the optical axis called the paraxial region. In this chapter we will consider, in general terms, the behavior of lenses with finite apertures and fields of view. It has been pointed out that well- corrected optical systems behave nearly according to the rules of paraxial imagery given in Chap. 2. This is another way of stating that a lens without aberrations forms an image of the size and in the loca- tion given by the equations for the paraxial or first-order region. We shall measure the aberrations by the amount by which rays miss the paraxial image point. It can be seen that aberrations may be determined by calculating the location of the paraxial image of an object point and then tracing a large number of rays (by the exact trigonometrical ray-tracing equa- tions of Chap. 10) to determine the amounts by which the rays depart from the paraxial image point. Stated this baldly, the mathematical determination of the aberrations of a lens which covered any reason- able field at a real aperture would seem a formidable task, involving an almost infinite amount of labor. However, by classifying the various types of image faults and by understanding the behavior of each type, the work of determining the aberrations of a lens system can be sim- plified greatly, since only a few rays need be traced to evaluate each aberration; thus the problem assumes more manageable proportions.
    [Show full text]
  • Ground-Based Photographic Monitoring
    United States Department of Agriculture Ground-Based Forest Service Pacific Northwest Research Station Photographic General Technical Report PNW-GTR-503 Monitoring May 2001 Frederick C. Hall Author Frederick C. Hall is senior plant ecologist, U.S. Department of Agriculture, Forest Service, Pacific Northwest Region, Natural Resources, P.O. Box 3623, Portland, Oregon 97208-3623. Paper prepared in cooperation with the Pacific Northwest Region. Abstract Hall, Frederick C. 2001 Ground-based photographic monitoring. Gen. Tech. Rep. PNW-GTR-503. Portland, OR: U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station. 340 p. Land management professionals (foresters, wildlife biologists, range managers, and land managers such as ranchers and forest land owners) often have need to evaluate their management activities. Photographic monitoring is a fast, simple, and effective way to determine if changes made to an area have been successful. Ground-based photo monitoring means using photographs taken at a specific site to monitor conditions or change. It may be divided into two systems: (1) comparison photos, whereby a photograph is used to compare a known condition with field conditions to estimate some parameter of the field condition; and (2) repeat photo- graphs, whereby several pictures are taken of the same tract of ground over time to detect change. Comparison systems deal with fuel loading, herbage utilization, and public reaction to scenery. Repeat photography is discussed in relation to land- scape, remote, and site-specific systems. Critical attributes of repeat photography are (1) maps to find the sampling location and of the photo monitoring layout; (2) documentation of the monitoring system to include purpose, camera and film, w e a t h e r, season, sampling technique, and equipment; and (3) precise replication of photographs.
    [Show full text]
  • AG-AF100 28Mm Wide Lens
    Contents 1. What change when you use the different imager size camera? 1. What happens? 2. Focal Length 2. Iris (F Stop) 3. Flange Back Adjustment 2. Why Bokeh occurs? 1. F Stop 2. Circle of confusion diameter limit 3. Airy Disc 4. Bokeh by Diffraction 5. 1/3” lens Response (Example) 6. What does In/Out of Focus mean? 7. Depth of Field 8. How to use Bokeh to shoot impressive pictures. 9. Note for AF100 shooting 3. Crop Factor 1. How to use Crop Factor 2. Foal Length and Depth of Field by Imager Size 3. What is the benefit of large sensor? 4. Appendix 1. Size of Imagers 2. Color Separation Filter 3. Sensitivity Comparison 4. ASA Sensitivity 5. Depth of Field Comparison by Imager Size 6. F Stop to get the same Depth of Field 7. Back Focus and Flange Back (Flange Focal Distance) 8. Distance Error by Flange Back Error 9. View Angle Formula 10. Conceptual Schema – Relationship between Iris and Resolution 11. What’s the difference between Video Camera Lens and Still Camera Lens 12. Depth of Field Formula 1.What changes when you use the different imager size camera? 1. Focal Length changes 58mm + + It becomes 35mm Full Frame Standard Lens (CANON, NIKON, LEICA etc.) AG-AF100 28mm Wide Lens 2. Iris (F Stop) changes *distance to object：2m Depth of Field changes *Iris：F4 2m 0m F4 F2 X X <35mm Still Camera> 0.26m 0.2m 0.4m 0.26m 0.2m F4 <4/3 inch> X 0.9m X F2 0.6m 0.4m 0.26m 0.2m Depth of Field 3.
    [Show full text]
  • Choosing Digital Camera Lenses Ron Patterson, Carbon County Ag/4-H Agent Stephen Sagers, Tooele County 4-H Agent
    June 2012 4H/Photography/2012-04pr Choosing Digital Camera Lenses Ron Patterson, Carbon County Ag/4-H Agent Stephen Sagers, Tooele County 4-H Agent the picture, such as wide angle, normal angle and Lenses may be the most critical component of the telescopic view. camera. The lens on a camera is a series of precision-shaped pieces of glass that, when placed together, can manipulate light and change the appearance of an image. Some cameras have removable lenses (interchangeable lenses) while other cameras have permanent lenses (fixed lenses). Fixed-lens cameras are limited in their versatility, but are generally much less expensive than a camera body with several potentially expensive lenses. (The cost for interchangeable lenses can range from $1-200 for standard lenses to $10,000 or more for high quality, professional lenses.) In addition, fixed-lens cameras are typically smaller and easier to pack around on sightseeing or recreational trips. Those who wish to become involved in fine art, fashion, portrait, landscape, or wildlife photography, would be wise to become familiar with the various types of lenses serious photographers use. The following discussion is mostly about interchangeable-lens cameras. However, understanding the concepts will help in understanding fixed-lens cameras as well. Figures 1 & 2. Figure 1 shows this camera at its minimum Lens Terms focal length of 4.7mm, while Figure 2 shows the110mm maximum focal length. While the discussion on lenses can become quite technical there are some terms that need to be Focal length refers to the distance from the optical understood to grasp basic optical concepts—focal center of the lens to the image sensor.
    [Show full text]
  • Digital Photography Basics for Beginners
    DIGITAL PHOTOGRAPHY BASICS FOR BEGINNERS by Robert Berdan [email protected] www.canadiannaturephotographer.com These notes are free to use by anyone learning or teaching photography. 1. Choosing a camera - there are 2 main types of compact cameras A) Point and Shoot Camera (some have interchangeable lenses most don't) - you view the scene on a liquid crystal display (LCD) screen, some cameras also offer viewfinders. B) Single Lens Reflex (SLR) - cameras with interchangeable lenses let you see the image through the lens that is attached to the camera. What you see is what you get - this feature is particularly valuable when you want to use different types of lenses. Digital SLR Camera with Interchangeable zoom lens 1 Point and shoot cameras are small, light weight and can be carried in a pocket. These cameras tend to be cheaper then SLR cameras. Many of these cameras offer a built in macro mode allowing extreme close-up pictures. Generally the quality of the images on compact cameras is not as good as that from SLR cameras, but they are capable of taking professional quality images. SLR cameras are bigger and usually more expensive. SLRs can be used with a wide variety of interchangeable lenses such as telephoto lenses and macro lenses. SLR cameras offer excellent image quality, lots of features and accessories (some might argue too many features). SLR cameras also shoot a higher frame rates then compact cameras making them better for action photography. Their disadvantages include: higher cost, larger size and weight. They are called Single Lens Reflex, because you see through the lens attached to the camera, the light is reflected by a mirror through a prism and then the viewfinder.
    [Show full text]
  • A Theoretical and Practical Introduction to Optics a Theoretical and Practical Introduction to Optics
    White Paper A Theoretical and Practical Introduction to Optics A Theoretical and Practical Introduction to Optics Be honest: do you really know how to calculate the focal length of a lens? If so, you are an exception to the rule and can stop reading here !! For the rest of you, here is a second chance. Back to square one "Piece of broken glass starts forest fire"– a common headline during the summer. But how could this have happened? Due to the enormous distance between the Earth and the Sun, the Sun only appears as a tiny point emitting parallel rays of light (figure 1a) Should these parallel rays pass through a lens (or a piece of glass, which has similar characteristics) the rays would meet behind the lens at what is called the focal point. But what happens if our point of light is so near to the lens that we can not assume to have parallel rays of light? They cross each other behind the focal point (figure 1b). If we take a look at the image of our point of light at the focal points position we will see a unclear blurred spot. And so the question arises- "what is focusing?". Focusing is to increase the distance between the focal plane and the lens until the focal plane and the junction of the rays overlap each other (figure 1c). Thus, for single points of light the situation is quite simple. But what happens to the image of screws, PCBs or plates of steel? From points of light to images A point of light does not necessarily originate directly from the sun, candles or lamps, it can also result from a reflection.
    [Show full text]
  • Camera Focal Length and the Perception of Pictures
    Ecological Psychology,26:30–46,2014 Copyright © Taylor & Francis Group, LLC ISSN: 1040-7413 print/1532-6969 online DOI: 10.1080/10407413.2014.877284 Camera Focal Length and the Perception of Pictures Martin S. Banks, Emily A. Cooper, and Elise A. Piazza Vision Science Program University of California, Berkeley Photographers, cinematographers, and computer-graphics engineers use certain techniques to create striking pictorial effects. By using lenses of different focal lengths, they can make a scene look compressed or expanded in depth, make afamiliarobjectlooknaturalordistorted,ormakeapersonlook smarter, more attractive, or more neurotic. Photographers have a rule of thumb that a 50 mm lens produces natural-looking pictures. We asked why pictures taken with a 50 mm lens look natural, while those taken with other focal lengths lookdistorted.Wefound that people’s preferred viewing distance when looking at pictures leads them to view long-focal-length pictures from too near and short-focal-length pictures from too far. Perceptual distortions occur because people do not take their incorrect viewing distances into account. By following the rule of thumb of using a 50 mm lens, photographers greatly increase the odds of a viewer looking at a photograph from the correct distance, where the percept will be undistorted. Our theory leads to new guidelines for creating pictorial effects that are more effective than conventional guidelines. Photographers, cinematographers, and computer-graphics engineers create pic- torial effects in various ways. For example, photographs of scenes captured with short-focal-length lenses appear expanded in depth, whereas those captured with long lenses appear compressed. These effects can be seen in still photographs and video.
    [Show full text]
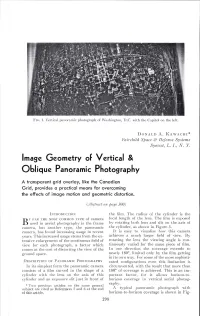
  • Image Geometry of Vertical & Oblique Panoramic Photography
    FIG. 1. Vertical panoramic photograph of Washington, D.C. with the Capitol on the left. DONALD A. KAWACHI* Fairchild Space & Defense Systems Syosset, L. I., N. Y. Image Geometry of Vertical & Oblique Panoramic Photography A transparent grid overlay, like the Canadian Grid, provides a practical means for overcoming the effects of image motion and geometric distortion. (Abstract on page 300) INTRODUCTION the fil m. The radius of the cylinder is the y FAR THE MOST COMMON TYPE of camera focal length of the lens. The fil m is exposed B used in aerial photography is the frame by rotating both lens and slit on the axis of camera, but another type, the panoramic the cylinder, as shown in Figure 3. camera, has found increasing usage in recent I t is easy to visualize how this camera years. This increased usage stems from the ex­ achieves a much larger field of view. By tensive enlargement of the continuous field of rotating the lens the viewing angle is con­ view for each photograph, a factor which tinuously varied for the same piece of film. comes at the cost of distorting the view of the In one direction the coverage extends to ground space. nearly 180°, limited only by the film getting in its own way. For some of the more sophisti­ DESCRIPTION OF PANORAMIC PHOTOGRAPHY cated configurations even this limitation is In its simplest form the panoramic camera circumvented, with the result that more than consists of a film curved in the shape of a 180° of coverage is achieved. This is an im­ cylinder with the lens on the axis of this portant factor, for it allows horizon-to­ cylinder and an exposure slit just in front of horizon coverage in vertical aerial photog­ raphy.
    [Show full text]
  • The F-Word in Optics
    The F-word in Optics F-number, was first found for fixing photographic exposure. But F/number is a far more flexible phenomenon for finding facts about optics. Douglas Goodman finds fertile field for fixes for frequent confusion for F/#. The F-word of optics is the F-number,* also known as F/number, F/#, etc. The F- number is not a natural physical quantity, it is not defined and used consistently, and it is often used in ways that are both wrong and confusing. Moreover, there is no need to use the F-number, since what it purports to describe can be specified rigorously and unambiguously with direction cosines. The F-number is usually defined as follows: focal length F-number= [1] entrance pupil diameter A further identification is usually made with ray angle. Referring to Figure 1, a ray from an object at infinity that is parallel to the axis in object space intersects the front principal plane at height Y and presumably leaves the rear principal plane at the same height. If f is the rear focal length, then the angle of the ray in image space θ′' is given by y tan θ'= [2] f In this equation, as in the others here, a sign convention for angles heights and magnifications is not rigorously enforced. Combining these equations gives: 1 F−= number [3] 2tanθ ' For an object not at infinity, by analogy, the F-number is often taken to be the half of the inverse of the tangent of the marginal ray angle. However, Eq. 2 is wrong.
    [Show full text]
  • Control of Chromatic Focal Shift Through Wavefront Coding Hans B. Wach, W
    Control of chromatic focal shift through wavefront coding Hans B. Wach, W. Thomas Cathey and Edward R. Dowski, Jr. Abstract Control of chromatic aberration through purely optical means is well known. We present a novel optical/digital method of controlling chromatic aberration. The optical/digital system, which incorporates a cubic phase modulation (CPM) plate in the optical system and post processing of the detected image, effectively reduces a system's sensitivity to misfocus in general or axial (longitudinal) chromatic aberration in particular. A fully achromatic imaging system ( one which is corrected for a continuous range of wavelengths ) can be achieved by initially correcting the optical system for lateral chromatic aberration through conventional techniques. Then the axial chromatic aberration is corrected by the inclusion of the CPM plate and post processing. 1. Introduction In general, optical system design consists of meeting specific requirements under some set of constraints. The constraints of a system vary from application to application. Cost, weight, size, number of optical elements, and materials comprising the optical elements are some typical constraints. Similarly, the performance requirements of a system are application dependent and often times include the minimization of aberrations. Some aberrations may or may not be important or they may be organized into a spectrum of tolerable to intolerable aberrations. Because meeting the system constraints can cause the aberrations to worsen and, conversely, minimizing the aberrations may require breaking the constraints, the challenge lies in making the tradeoff between the two. For example, the design of a digital color imaging system which uses only plastic optical elements is a nontrivial task.
    [Show full text]
  • TECHSPEC® Fixed Focal Length Lenses
    Edmund Optics® BROCHURE FIXED FOCAL LENGTH LENSES ® COPYRIGHT 2017 EDMUND OPTICS, INC. ALL RIGHTS RESERVED 7/17 RIGHTS RESERVED ALL 2017 EDMUND OPTICS, INC. ® COPYRIGHT INNOVATION STARTS HERE . Global Design & Support | Rapid Prototyping Volume Manufacturing & Pricing Contact us for a Stock or Custom Quote Today! USA: +1-856-547-3488 | EUROPE: +44 (0) 1904 788600 ASIA: +65 6273 6644 | JAPAN: +81-3-3944-6210 www.edmundoptics.com/fixed-focal UC SERIES FIXED FOCAL LENGTH LENSES • Ultra-Compact (UC) Form Factor • 4K Resolution Designed for Small Pixels (≤2.2µm) • Optimized for 1/2•5" Sensors and Supports up to 1/1•8" Our ultra-compact, TECHSPEC® UC Series Fixed Focal Length Lenses are designed to optimize performance, cost, and size without sacrificing quality or feel. Designed for pixels that are ≤2.2μm, these lenses provide high levels of resolution (>200 lp/mm) across the sensor and are compatible with all standard C-Mount cameras. TECHSPEC® UC Series Fixed Focal Length Lenses feature focus and iris adjustments, as well as re- cessed set screws, and are manufactured for use at typical machine vision working distances. While they are optimized for 1/2.5" sensors, many focal lengths will work on sensors up to 1/1.8". The TECHSPEC® UC Series lenses are an outstanding option for use on all smaller format camera sensors, along with both short and long working dis- tance applications, making them ideal for inspection, factory automation, biomedical devices, and a broad range of other applications. Dimensions Units: mm Focal Length A B C D Filter Thread Focus Adjustment Iris Locking Screw Iris Adjustment Focus Locking Screw C-Mount 4mm 40 40.6 30 2.8 M62.0 x 0.75 with required filter adapter #33-308 6mm 36 40.9 30 3.2 M34.0 x 0.5 Max.
    [Show full text]