DOCSLIB.ORG

Impact Cratering the Effect of Crustal Strength and Planetary Gravity

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Impact Cratering the Effect of Crustal Strength and Planetary Gravity REVIEWS OF GEOPHYSICS AND SPACE PHYSICS, VOL. 19, NO. 1, PAGES 1-12, FEBRUARY 1981 Impact Cratering: The Effect of Crustal Strengthand Planetary Gravity JOHN D. O'KEEFE AND THOMAS J. AHRENS SeismologicalLaboratory, California Institute of Technology,Pasadena, California 91125 Upon impactof a meteoritewith a planetarysurface the resultingshock wave both 'processes'the ma- terial in the vicinity of the impact and setsa larger volume of material than was subjectedto high pres- sureinto motion. Most of the volume which is excavatedby the impact leavesthe crater after the shock wave hasdecayed. The kineticenergy which hasbeen deposited in the planetarysurface is convertedinto reversibleand irreversiblework, carriedout againstthe planetarygravity field and againstthe strengthof the impactedmaterial, respectively. By usingthe resultsof compressibleflow calculationsprescribing the initial stagesof the impact interaction(obtained with finite differencetechniques) the final stagesof cra- tering flow along the symmetryaxis are described,using the incompressibleflow formalismproposed by Maxwell. The fundamentalassumption in this descriptionis that the amplitude of the particle velocity field decreaseswith time as kinetic energyis convertedinto heat and gravitationalpotential energy. At a given time in a sphericalcoordinate system the radial velocity is proportional to R -z, where R is the radius (normalizedby projectilevelocity) and z is a constantshape factor for the duration of flow and a weak function of angle. The azimuthal velocity, as well as the streamlines,is prescribedby the in- compressibilitycondition. The final crater depth (for fixed strength Y) is found to be proportional to Ro[2(z+ l)Uor2/g]l/(z+l), whereUor is the initial radialparticle velocity at (projectilenormalized) radius P,o,g is planetarygravity, and z (which varied from 2 to 3) is the shapefactor. The final craterdepth (for fixedgravity) is alsofound to be proportionalto [PUor2/Yz]l/(z+•), where p and Y are planetarydensity and yield strength,respectively. By usinga Mohr-Coulomb yield criterionthe effectof varying strength on transientcrater depth and on craterformation time in the gravity field of the moon is investigatedfor 5-km/s impactorswith radii in the 10-to 107-cmrange. Comparison of craterformation time and maxi- mumtransient crater depth as a functionof gravityyields dependencies proportional to g-O.SSand g-O.•9, respectively,compared to g-O.61sand g-O. 165 observed by Gault and Wedekindfor hypervelocityimpact cratersin the 16- to 26-cm-diameterrange in a quartz sand (with Mohr-Coulomb type behavior) carried out overan effectivegravity range of 72-980 cm/s2. 1. INTRODUCTION at sizesand time scalesfor which gravity does not affect the In order to obtain the relative ages of cratered surfaces flow. Theoretically basedscaling laws for relating final crater formed on different terraneson a singleplanet [e.g., Neukum, dimensionsto target and projectiledensities and projectileki- 1977], as well as to obtain meaningful interplanetary com- netic energyor momentum(or a combinationof these),plan- parisons[e.g., Gault et al., 1975;Neukum and Wise, 1976], the etary gravity, sound speed,and material strengthhave been effect of planetary crustal strengthand gravity on the dimen- developed on the basis of laboratory and field data [e.g., sionsof cratersmust be understood.Because the largestman- Chabai, 1965;Gault, 1973;Gault et al., 1975;O'Keefe and Ah- made impact craters(produced on the moon by empty rocket rens, 1978]. casings)are only some40 m in diameter [Whitaker, 1972] and In the presentpaper we examine how maximum transient the largestnuclear explosions(formed in wet coral sand) are crater depthis relatedto projectileenergy for a rangeof plan- only 1.8 km in diameter [F'aile, 1961], the experimental data etary gravities and crustal strengthconditions. Moreover, we available are limited, and theoretical estimates must be used examine how the scalinglaws themselvesdepend on gravity to understandcrater populations. and target strength.Although, in principle, sucha studycould There have been a number of studiesentailing the analyti- be carried out by using only the finite difference numerical cal and numerical prediction of crateringphenomena and the methodspreviously applied to meteoriteimpact crateringon scalingof laboratory experimentaldata to planetary cratering. the earth and the terrestrialplanets [Bjork, 1961;O'Keefe and In order to test theories [e.g., Chabai, 1965] of scaling of the Ahrens, 1975, 1976, 1977a, b, 1978; Swift, 1977; Bryan et al., sizesof explosive(and impact) cratersin a variety of gravita- 1978],this would be computationallyuneconomical. The ap- tional fields, centimeterscale explosion cratering experiments proach taken is (1) to establishthe validity for impact crater- have been carried out under conditions both less than the ing of the Maxwell z model,which was previously applied t6 earth's gravity field [Johnsonet al., 1969;Gault and Wedekind, explosivecratering by Maxwell [1973, 1977]and Maxwell and 1977] and greater than the earth's gravity field [F'ictorovand Seifert [1976], (2) to compute the partitioning of impact en- Stepenov,1960; Schmidtand Holsapple, 1980]. The effect of ergy into gravitationalpotential energy for large-scalecrater- rock or soil strengthon laboratory cratering experimentshas ing and the effect of weakening of planetary material via been addressedby Moore et al. [1964], Gaffhey [1979], and 'shock processing,'and (3) to make a comparisonof calcu- Holsapple and Schmidt [1979], and on the basis of extensive lated and laboratorycrater excavationtimes and depths.The numerical calculations the scaling of hypervelocity impact physicalbasis for the incompressibleflow descriptionof late craters is discussedby Dienes and Walsh [1970]. In the latter stagecratering processesis describedin detail in the next sec- paper the conditionsare describedfor similitudeof the hydro- tion. Specifically,we use the incompressibleformalism to ex- dynamicflows inducedby hypervelocityimpacts in materials amine the effectsof planetary crustal strengthand gravity on the moon and to comparecalculational results with laboratory Copyright¸ 1981 by the American GeophysicalUnion. cratering experiments. Paper number 80R 1189. 0034-6853/81/080R- 1189506.00 2 O'KEEFEAND AHRENS:CRATERING, STRENGTH, AND GRAVITY ,-Trans•entCavity / /-Transient i / ß • VelocityScales D•ista •//• (a'n) Fig. 1. Incompressibleflow field crateringmodel. (a) Particlevelocity vectors for R0 -- 1 m, a -- 10 m/s, and z -- 3 for 0 = 0ø-110ø. (b) Streamlinesfor incompressibleflow for Ro = 1 m, a = 10 m/s, and z = 2. 2. LATE STAGE CRATERING FLOW whereR is the projectile-normalizedradius, a(t) is a parame- The z Model ter which dependson the strengthof the flow, and z is a con- stantfor a givenstreamline which specifiesthe shapeof the Bjork et aL [ 1967] first pointed out that the impact of a me- streamline.The validity of the latter statementcan be demon- teorite with a solid half space,such as a planetary surface,sets stratedby consideringthe divergenceof the flow (equal to a large region of the target into motion after the shock wave zero on accountof the incompressibilityassumption) in two- has 'processed'a portion of target (planetary material) in the dimensionalspherical coordinates: immediate vicinity of the impact and that this large region is much greater in size than that which experiencedpeak dy- 0 = SinO0(ReUr)/OR + RO(sin 0 uo)/00 (2) namic pressures.The decaying shock wave propagatesaway from the immediate region of impact and becomes'detached' where0 and uoare definedin Figurel a. Substituting(1) into (2) and integratingover the angular range 0-0 of the flow from the impactor. Thus a large low-stressregion which was set into motion by the shockwave becomesinvolved in crater excavation. Once the initial impact-inducedparticle velocity (2 -- 2)Ur Sin0 dO= d(sin0 u0) (3) flow in the target has been establishedand the stresseshave f0 fo decayed such that the kinetic energy per unit mass is much yields,for the azimuthalparticle velocity, greater than recoverablestrain energy, the size of the crater producedis solelycontrolled by conservationof energyfor a uo-- R dO/dt= sin 0 (z - 2)Ur/(I q- COS0) (4) fixed geometry, as was suggestedin an early model of crater- ing by Charters and Summers [1959]. We assumein the in- Again substitutingdR/dt for Urin (4) and integratingfrom 0o compressiblelate stageflow z model that the kinetic energyof to 0 and Roto R, the trajectoryof a streamline(Figure lb) is the mass of target material along a given flow streamline is given by equal to the irreversiblework that is performed against the (a/ao)(•-2) = (1 - cos•)/(1 - cos00) (5) material due to its finite strengthplus the work done against the planetary gravity field. Since the total kinetic energy im- As is shownin Figure la, R0 and 0orefer to a point on a refer- parted to the impacted target region is bounded as a result of encesurface which is takento be on the boundaryof the cra- the initial shockand rarefactionwave interaction,the equality ter transientcavity at a givenreference time. The time depen- of initial kinetic energy along a streamlinewith the irrevers- dence of the particle radial position can be obtained by ible work done againstthe material strengthand the planetary integrating(1) to yield gravity field limits the final crater dimensions. The key to utilizing the conservationof energyconcept de- R(t)•+'- Ro(to):+'= (z + 1) a(t) dt -- (z + (6) scribedqualitatively above
Load more

Recommended publications
  • LUNAR INTERACTIONS ABSTRACTS of PAPERS PRESENTED at the CONFERENCE on INTERACTIONS of the INTERPLANETARY PLASMA with the MODERN and ANCIENT MOON
    LUNAR INTERACTIONS ABSTRACTS OF PAPERS PRESENTED AT THE CONFERENCE ON INTERACTIONS OF THE INTERPLANETARY PLASMA with the MODERN AND ANCIENT MOON ORGANIZED BY THE I. N 3 LUNAR SCIENCE INSTITUTE m I 3 AND THE I- 2 SPACE PHYSICS DEPARTMENT RICE UNIVERSITY sponsored by the NATIONAL AERONAUTICS m m AND 0 .. I-( OIW mrl SPACE ADMINISTRATION ZX CV OH IOI H WclU AND THE uux- V&H 0 NATIONAL SCIENCE FOUNDATION g,,,, wm. WWO@W u u ? ZZLOX€e HW5H vlOHU ffiMHrnfC 4 ffi H 2.~4~4a Edited by 3 dz ,.aV)ffiuJO ffiwcstn WPt.4" DAVID R. CRISWELL ,!a !a Pl r 4 W Pa4 %- rn ZW. and Or=4OcC+J fO Hi4 r WWF I rnU2.M ffiBZ* JOHN W. FREEMAN UUW4aJ I amor 0 alffiwffi E REPRODUCTION RESTRICTIONS OVERRIDDEN 2Z~OZ E 2 2 .: u Bmscientific ma Technical Information FaciLitX -eu $4 to) Copyright O 1974 by the Lunar Science Institute Conference held at George Williams College Lake Geneva Campus Williams Bay, Wisconsin 30 September - 4 October 1974 Compiled by and available from The Lunar Science Institute 3303 Nasa Road 1 Houston, Texas 77058 PREFACE The field of lunar science has essentially completed a period of exponential growth promoted by the national efforts of the 1960's to land on the moon. As normally happens in a diverse scientific community, the interpretations of specialized lunar data have reflected the precepts in the various specialized fields. Constant promotion of the broadest overviews between these diverse fields is appropriate to identify processes or phenomenon recog- nized in one avenue of investigation which may have great importance in explaining the data of other specialities.
    [Show full text]
  • Inis: Terminology Charts
    IAEA-INIS-13A(Rev.0) XA0400071 INIS: TERMINOLOGY CHARTS agree INTERNATIONAL ATOMIC ENERGY AGENCY, VIENNA, AUGUST 1970 INISs TERMINOLOGY CHARTS TABLE OF CONTENTS FOREWORD ... ......... *.* 1 PREFACE 2 INTRODUCTION ... .... *a ... oo 3 LIST OF SUBJECT FIELDS REPRESENTED BY THE CHARTS ........ 5 GENERAL DESCRIPTOR INDEX ................ 9*999.9o.ooo .... 7 FOREWORD This document is one in a series of publications known as the INIS Reference Series. It is to be used in conjunction with the indexing manual 1) and the thesaurus 2) for the preparation of INIS input by national and regional centrea. The thesaurus and terminology charts in their first edition (Rev.0) were produced as the result of an agreement between the International Atomic Energy Agency (IAEA) and the European Atomic Energy Community (Euratom). Except for minor changesq the terminology and the interrela- tionships btween rms are those of the December 1969 edition of the Euratom Thesaurus 3) In all matters of subject indexing and ontrol, the IAEA followed the recommendations of Euratom for these charts. Credit and responsibility for the present version of these charts must go to Euratom. Suggestions for improvement from all interested parties. particularly those that are contributing to or utilizing the INIS magnetic-tape services are welcomed. These should be addressed to: The Thesaurus Speoialist/INIS Section Division of Scientific and Tohnioal Information International Atomic Energy Agency P.O. Box 590 A-1011 Vienna, Austria International Atomic Energy Agency Division of Sientific and Technical Information INIS Section June 1970 1) IAEA-INIS-12 (INIS: Manual for Indexing) 2) IAEA-INIS-13 (INIS: Thesaurus) 3) EURATOM Thesaurusq, Euratom Nuclear Documentation System.
    [Show full text]
  • Impact Crater Collapse
    P1: SKH/tah P2: KKK/mbg QC: KKK/arun T1: KKK March 12, 1999 17:54 Annual Reviews AR081-12 Annu. Rev. Earth Planet. Sci. 1999. 27:385–415 Copyright c 1999 by Annual Reviews. All rights reserved IMPACT CRATER COLLAPSE H. J. Melosh Lunar and Planetary Laboratory, University of Arizona, Tucson, AZ 85721; e-mail: [email protected] B. A. Ivanov Institute for Dynamics of the Geospheres, Russian Academy of Sciences, Moscow, Russia 117979 KEY WORDS: crater morphology, dynamical weakening, acoustic fluidization, transient crater, central peaks ABSTRACT The detailed morphology of impact craters is now believed to be mainly caused by the collapse of a geometrically simple, bowl-shaped “transient crater.” The transient crater forms immediately after the impact. In small craters, those less than approximately 15 km diameter on the Moon, the steepest part of the rim collapses into the crater bowl to produce a lens of broken rock in an otherwise unmodified transient crater. Such craters are called “simple” and have a depth- to-diameter ratio near 1:5. Large craters collapse more spectacularly, giving rise to central peaks, wall terraces, and internal rings in still larger craters. These are called “complex” craters. The transition between simple and complex craters depends on 1/g, suggesting that the collapse occurs when a strength threshold is exceeded. The apparent strength, however, is very low: only a few bars, and with little or no internal friction. This behavior requires a mechanism for tem- porary strength degradation in the rocks surrounding the impact site. Several models for this process, including acoustic fluidization and shock weakening, have been considered by recent investigations.
    [Show full text]
  • Redalyc.Guillaume Amontons
    Revista CENIC. Ciencias Químicas ISSN: 1015-8553 [email protected] Centro Nacional de Investigaciones Científicas Cuba Wisniak, Jaime Guillaume Amontons Revista CENIC. Ciencias Químicas, vol. 36, núm. 3, 2005, pp. 187-195 Centro Nacional de Investigaciones Científicas La Habana, Cuba Disponible en: http://www.redalyc.org/articulo.oa?id=181620584008 Cómo citar el artículo Número completo Sistema de Información Científica Más información del artículo Red de Revistas Científicas de América Latina, el Caribe, España y Portugal Página de la revista en redalyc.org Proyecto académico sin fines de lucro, desarrollado bajo la iniciativa de acceso abierto Revista CENIC Ciencias Químicas, Vol. 36, No. 3, 2005. Guillaume Amontons Jaime Wisniak. Department of Chemical Engineering, Ben-Gurion University of the Negev, Beer-Sheva, Israel 84105. [email protected] Recibido: 24 de agosto de 2004. Aceptado: 28 de octubre de 2004. Palabras clave: barómetro, termometría, cero absoluto, higrómetro, telégrafo, máquina de combustión externa, fricción en las máquinas. Key words: barometer, thermometry, absolute zero, hygrometer, telegraph, external-combustion machine, friction in machines. RESUMEN. Guillaume Amontons (1663-1705) fue un experimentador que se de- Many instruments had been de- dicó a la mejora de instrumentos usados en física, en particular, el barómetro y el veloped to measure in a gross man- termómetro. Dentro de ellos se destacan, en particular, un barómetro plegable, ner the humidity of air. Almost all un barómetro sin cisterna para usos marítimos, y un higrómetro. Experimentó systems made use of the hygro- con el termómetro de aire e hizo notar que con dicho aparato el máximo frío sería scopic properties of vegetable or aquel que reduciría el resorte (presión) del aire a cero, siendo así, el primero que animal fibers such as hemp, oats, dedujo la presencia de un cero absoluto de temperatura.
    [Show full text]
  • Ages of Large Lunar Impact Craters and Implications for Bombardment During the Moon’S Middle Age ⇑ Michelle R
    Icarus 225 (2013) 325–341 Contents lists available at SciVerse ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Ages of large lunar impact craters and implications for bombardment during the Moon’s middle age ⇑ Michelle R. Kirchoff , Clark R. Chapman, Simone Marchi, Kristen M. Curtis, Brian Enke, William F. Bottke Southwest Research Institute, 1050 Walnut Street, Suite 300, Boulder, CO 80302, United States article info abstract Article history: Standard lunar chronologies, based on combining lunar sample radiometric ages with impact crater den- Received 20 October 2012 sities of inferred associated units, have lately been questioned about the robustness of their interpreta- Revised 28 February 2013 tions of the temporal dependance of the lunar impact flux. In particular, there has been increasing focus Accepted 10 March 2013 on the ‘‘middle age’’ of lunar bombardment, from the end of the Late Heavy Bombardment (3.8 Ga) until Available online 1 April 2013 comparatively recent times (1 Ga). To gain a better understanding of impact flux in this time period, we determined and analyzed the cratering ages of selected terrains on the Moon. We required distinct ter- Keywords: rains with random locations and areas large enough to achieve good statistics for the small, superposed Moon, Surface crater size–frequency distributions to be compiled. Therefore, we selected 40 lunar craters with diameter Cratering Impact processes 90 km and determined the model ages of their floors by measuring the density of superposed craters using the Lunar Reconnaissance Orbiter Wide Angle Camera mosaic. Absolute model ages were computed using the Model Production Function of Marchi et al.
    [Show full text]
  • Lunar Impact Basins Revealed by Gravity Recovery and Interior
    Lunar impact basins revealed by Gravity Recovery and Interior Laboratory measurements Gregory Neumann, Maria Zuber, Mark Wieczorek, James Head, David Baker, Sean Solomon, David Smith, Frank Lemoine, Erwan Mazarico, Terence Sabaka, et al. To cite this version: Gregory Neumann, Maria Zuber, Mark Wieczorek, James Head, David Baker, et al.. Lunar im- pact basins revealed by Gravity Recovery and Interior Laboratory measurements. Science Advances , American Association for the Advancement of Science (AAAS), 2015, 1 (9), pp.e1500852. 10.1126/sci- adv.1500852. hal-02458613 HAL Id: hal-02458613 https://hal.archives-ouvertes.fr/hal-02458613 Submitted on 26 Jun 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. RESEARCH ARTICLE PLANETARY SCIENCE 2015 © The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. Distributed Lunar impact basins revealed by Gravity under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC). Recovery and Interior Laboratory measurements 10.1126/sciadv.1500852 Gregory A. Neumann,1* Maria T. Zuber,2 Mark A. Wieczorek,3 James W. Head,4 David M. H. Baker,4 Sean C. Solomon,5,6 David E. Smith,2 Frank G.
    [Show full text]
  • GRAIL Gravity Observations of the Transition from Complex Crater to Peak-Ring Basin on the Moon: Implications for Crustal Structure and Impact Basin Formation
    Icarus 292 (2017) 54–73 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus GRAIL gravity observations of the transition from complex crater to peak-ring basin on the Moon: Implications for crustal structure and impact basin formation ∗ David M.H. Baker a,b, , James W. Head a, Roger J. Phillips c, Gregory A. Neumann b, Carver J. Bierson d, David E. Smith e, Maria T. Zuber e a Department of Geological Sciences, Brown University, Providence, RI 02912, USA b NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA c Department of Earth and Planetary Sciences and McDonnell Center for the Space Sciences, Washington University, St. Louis, MO 63130, USA d Department of Earth and Planetary Sciences, University of California, Santa Cruz, CA 95064, USA e Department of Earth, Atmospheric and Planetary Sciences, MIT, Cambridge, MA 02139, USA a r t i c l e i n f o a b s t r a c t Article history: High-resolution gravity data from the Gravity Recovery and Interior Laboratory (GRAIL) mission provide Received 14 September 2016 the opportunity to analyze the detailed gravity and crustal structure of impact features in the morpho- Revised 1 March 2017 logical transition from complex craters to peak-ring basins on the Moon. We calculate average radial Accepted 21 March 2017 profiles of free-air anomalies and Bouguer anomalies for peak-ring basins, protobasins, and the largest Available online 22 March 2017 complex craters. Complex craters and protobasins have free-air anomalies that are positively correlated with surface topography, unlike the prominent lunar mascons (positive free-air anomalies in areas of low elevation) associated with large basins.
    [Show full text]
  • Science Concept 3: Key Planetary
    Science Concept 6: The Moon is an Accessible Laboratory for Studying the Impact Process on Planetary Scales Science Concept 6: The Moon is an accessible laboratory for studying the impact process on planetary scales Science Goals: a. Characterize the existence and extent of melt sheet differentiation. b. Determine the structure of multi-ring impact basins. c. Quantify the effects of planetary characteristics (composition, density, impact velocities) on crater formation and morphology. d. Measure the extent of lateral and vertical mixing of local and ejecta material. INTRODUCTION Impact cratering is a fundamental geological process which is ubiquitous throughout the Solar System. Impacts have been linked with the formation of bodies (e.g. the Moon; Hartmann and Davis, 1975), terrestrial mass extinctions (e.g. the Cretaceous-Tertiary boundary extinction; Alvarez et al., 1980), and even proposed as a transfer mechanism for life between planetary bodies (Chyba et al., 1994). However, the importance of impacts and impact cratering has only been realized within the last 50 or so years. Here we briefly introduce the topic of impact cratering. The main crater types and their features are outlined as well as their formation mechanisms. Scaling laws, which attempt to link impacts at a variety of scales, are also introduced. Finally, we note the lack of extraterrestrial crater samples and how Science Concept 6 addresses this. Crater Types There are three distinct crater types: simple craters, complex craters, and multi-ring basins (Fig. 6.1). The type of crater produced in an impact is dependent upon the size, density, and speed of the impactor, as well as the strength and gravitational field of the target.
    [Show full text]
  • Constraining the Evolutionary History of the Moon and the Inner Solar System: a Case for New Returned Lunar Samples
    Constraining the Evolutionary History of the Moon and the Inner Solar System: A Case for New Returned Lunar Samples The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Tartèse, Romain, et al. "Constraining the Evolutionary History of the Moon and the Inner Solar System: A Case for New Returned Lunar Samples." Space Science Reviews, 215 (December 2019): 54. © 2019, The Author(s). As Published http://dx.doi.org/10.1007/s11214-019-0622-x Publisher Springer Science and Business Media LLC Version Final published version Citable link https://hdl.handle.net/1721.1/125329 Terms of Use Creative Commons Attribution 4.0 International license Detailed Terms https://creativecommons.org/licenses/by/4.0/ Space Sci Rev (2019) 215:54 https://doi.org/10.1007/s11214-019-0622-x Constraining the Evolutionary History of the Moon and the Inner Solar System: A Case for New Returned Lunar Samples Romain Tartèse1 · Mahesh Anand2,3 · Jérôme Gattacceca4 · Katherine H. Joy1 · James I. Mortimer2 · John F. Pernet-Fisher1 · Sara Russell3 · Joshua F. Snape5 · Benjamin P. Weiss6 Received: 23 August 2019 / Accepted: 25 November 2019 / Published online: 2 December 2019 © The Author(s) 2019 Abstract The Moon is the only planetary body other than the Earth for which samples have been collected in situ by humans and robotic missions and returned to Earth. Scien- tific investigations of the first lunar samples returned by the Apollo 11 astronauts 50 years ago transformed the way we think most planetary bodies form and evolve. Identification of anorthositic clasts in Apollo 11 samples led to the formulation of the magma ocean concept, and by extension the idea that the Moon experienced large-scale melting and differentiation.
    [Show full text]
  • Quantum Field Theory As Eigenvalue Problem
    Quantum ¯eld theory as eigenvalue problem Arnold Neumaier Institut furÄ Mathematik, UniversitÄat Wien Strudlhofgasse 4, A-1090 Wien, Austria email: [email protected] WWW: http://www.mat.univie.ac.at/ neum/ » March 10, 2003 Abstract. A mathematically well-de¯ned, manifestly covariant theory of classical and quan- tum ¯eld is given, based on Euclidean Poisson algebras and a generalization of the Ehrenfest equation, which implies the stationary action principle. The theory opens a constructive spec- tral approach to ¯nding physical states both in relativistic quantum ¯eld theories and for exible phenomenological few-particle approximations. In particular, we obtain a Lorentz-covariant phenomenological multiparticle quantum dynam- ics for electromagnetic and gravitational interaction which provides a representation of the Poincar¶e group without negative energy states. The dynamics reduces in the nonrelativis- tic limit to the traditional Hamiltonian multiparticle description with standard Newton and Coulomb forces. The key that allows us to overcome the traditional problems in canonical quantization is the fact that we use the algebra of linear operators on a space of wave functions slightly bigger than traditional Fock spaces. Keywords: action, axiomatic physics, classical ¯eld, classical limit, conservative quantum state, constrained SchrÄodinger equation, covariant interaction, deformation quantization, density, multiparticle Dirac equation, Ehrenfest equation, eigenvalue problem, electrodynamics, Euclidean Poisson algebra,
    [Show full text]
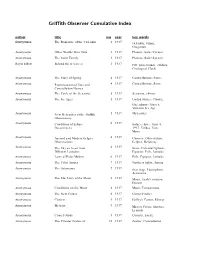
  • Griffith Observer Cumulative Index
    Griffith Observer Cumulative Index author title mo year key words Anonymous The Romance of the Calendar 2 1937 calendar, Julian, Gregorian Anonymous Other Worlds than Ours 3 1937 Planets, Solar System Anonymous The S ola r Fa mily 3 1937 Planets, Solar System Roya l Elliott Behind the Sciences 3 1937 GO, pla ne ta rium, e xhibits , Ge ologica l Clock Anonymous The Stars of Spring 4 1937 Cons te lla tions , S ta rs , Anonymous Pronunciation of Star and 4 1937 Cons te lla tions , S ta rs Constellation Names Anonymous The Cycle of the Seasons 5 1937 Seasons, climate Anonymous The Ice Ages 5 1937 United States, Climate, Greenhouse Gases, Volcano, Ice Age Anonymous New Meteorites at the Griffith 5 1937 Meteorites Observatory Anonymous Conditions of Eclipse 6 1937 Solar eclipse, June 8, Occurrences 1937, Umbra, Sun, Moon Anonymous Ancient and Modern Eclipse 6 1937 Chinese, Observation, Observations Eclips e , Re la tivity Anonymous The Sky as Seen from 6 1937 Stars, Celestial Sphere, Different Latitudes Equator, Pole, Latitude Anonymous Laws of Polar Motion 6 1937 Pole, Equator, Latitude Anonymous The Polar Aurora 7 1937 Northern lights, Aurora Anonymous The Astrorama 7 1937 Star map, Planisphere, Astrorama Anonymous The Life Story of the Moon 8 1937 Moon, Earth's rotation, Darwin Anonymous Conditions on the Moon 8 1937 Moon, Temperature, Anonymous The New Comet 8 1937 Come t Fins le r Anonymous Comets 9 1937 Halley's Comet, Meteor Anonymous Meteors 9 1937 Meteor Crater, Shower, Leonids Anonymous Comet Orbits 9 1937 Comets, Encke Anonymous
    [Show full text]
  • Science Concept 3: Key Planetary Processes Are Manifested in the Diversity of Lunar Crustal Rocks
    Science Concept 3: Key Planetary Processes are Manifested in the Diversity of Lunar Crustal Rocks Science Concept 3: Key planetary processes are manifested in the diversity of crustal rocks Science Goals: a. Determine the extent and composition of the primary feldspathic crust, KREEP layer, and other products of differentiation. b. Inventory the variety, age, distribution, and origin of lunar rock types. c. Determine the composition of the lower crust and bulk Moon. d. Quantify the local and regional complexity of the current lunar crust. e. Determine the vertical extent and structure of the megaregolith. INTRODUCTION Formation and Evolution of the Moon The Moon is a unique environment, preserving crucial information about the early history and later evolution of the solar system. The lack of major surficial tectonic processes within the past few billion years or so, as well as the lack of significant quantities of surface water, have allowed for excellent preservation of the lithologies and geomorphological features that formed during the major planetary formation events. Fundamental discoveries during the Apollo program showed that the Moon is made up of a variety of volcanic and impact rock types that exhibit a particular range of chemical and mineralogical compositions. The key planetary processes conveyed by this diversity include planetary differentiation, volcanism, and impact cratering. Analysis of Apollo, Luna, and lunar meteoritic samples, as well as orbital data from a series of lunar exploration missions, generated geophysical models that strove to tell the story of the Moon. However, such models are restricted in the sense that they are based on information gathered from the samples that have so far been acquired.
    [Show full text]