DOCSLIB.ORG

The Multivariate Split Normal Distribution and Asymmetric Principal Components Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Multivariate Split Normal Distribution and Asymmetric Principal Components Analysis SVERIGES RIKSBANK WORKING PAPER SERIES 175 The Multivariate Split Normal Distribution and Asymmetric Principal Components Analysis Mattias Villani and Rolf Larsson DECEMBER 2004 WORKING PAPERS ARE OBTAINABLE FROM Sveriges Riksbank • Information Riksbank • SE-103 37 Stockholm Fax international: +46 8 787 05 26 Telephone international: +46 8 787 01 00 E-mail: [email protected] The Working Paper series presents reports on matters in the sphere of activities of the Riksbank that are considered to be of interest to a wider public. The papers are to be regarded as reports on ongoing studies and the authors will be pleased to receive comments. The views expressed in Working Papers are solely the responsibility of the authors and should not to be interpreted as reflecting the views of the Executive Board of Sveriges Riksbank. t mç s ç nê é ç d Éêè è aéé p è ç cêé êèè aè çt m vçç è è rêç l êè s à r É è wê èà p s nêN QWU déÉ RPPT aÉ t éç ç èê é ç Éêè è ç éç èê é ç Éêè É ê é ççê ê è è ê é ê êè êèOç êè çêèà É ê è ç N t êé ê ê ÉêèL èçèà éêéè àè èà èêèL éç è è ê N m éé ççêê é êè è êé ç b è è ç ê éç ç èê é ç éêç çê N )*ê Z b è è èL eç êèL e é êèL m éé ççêêL mç è ç L è N jel ç êèZ c""L c"VN #t $ ê à çç èêçà $è è ç ê êé cêèç ê r è hé èM è ê ç è (h frIL à è èêN fP,-.O"/// è r cêèç (0è 1I à è èêN 2".M.PP.M"PP3N t è êçç êè Éç ê ê è êç èê É è 4èà ê e bê ê à r É èN sà r É è L r éèL seMQPS SW sê êçéL sèL è d éè ê s L sê M êçé uè N eMé çZ é N çç è5 É èN N d éè ê ièêé êè sèL u ç uè L bê ,"SL eM3," .P u ç L èN eMé çZ êçNç êè5 NN N R mattias villani and rolf larsson QN ièïìêÖñÑïäêè a èÇïñìÇç ÖäìÜÑïäêè áêì ÜôïÜèÖäèà ïâÜ èêìéÇç ÖäîïìäÉñïäêè äî ïâÜ äèïìêÖñÑïäêè êá îêéÜ îêìï êá îåÜòèÜîîL ÇèÖ îÜóÜìÇç ëìêëêîÇçî âÇóÜ äèÖÜÜÖ ÜéÜìàÜÖL Éêïâ äè ïâÜ ñèäóÇìäÇïÜ ÇèÖ éñçïäóÇìäÇïÜ îÜïïäèàL îÜÜ NàN aõõÇçäèä HQYXUI ÇèÖ aõõÇçäèä ÇèÖ dÇççÇ vÇççÜ HQYYVIN aéêèà ïâêîÜ äî ïâÜ îëçäï èêìéÇç ÖäîïìäÉñïäêèL êì ïâÜ ïòêMëäÜÑÜ èêìéÇçL êìäàäèÇççö äèïìêÖñÑÜÖ Éö gäÉÉêèî ÇèÖ möçìêäÜ HQYWSIL òäïâ éêîï êá äïî åèêòè ëìêëÜìïäÜî ÖÜìäóÜÖ Éö jêâè HQYXRI[ îÜÜ Ççîê käéÉÜì HQYXUI áêì îêéÜ ÇÖÖäïäêèÇç ìÜîñçïîN jêâèîêèL kêïõ ÇèÖ bÇçÇåìäîâèÇè HQYYTI ÑêèïÇäèî ìÜáÜìÜèÑÜî ïê ëÇëÜìî òâÜìÜ ïâÜ îëçäï èêìéÇç ÖäîïìäÉñïäêè äî ñîÜÖ Çî Ç îïÇïäîïäÑÇç éêÖÜçN tâÜ ÜÇîäçö äèïÜìëìÜïÜÖ áêìé êá ïâÜ îëçäï èêìéÇç Öäîïìä!êè âÇ % % !8% ! (6 ())*,4 5L 9 : ())-,, # % % 4 ÜNàN !% && 6 (;;;, 5 Üï ÇçN ())-, 6# $ < " % 8" ())-, = && 9 $ 0#" ()*), % ' & ! ! & / # / % & ! && # & && % && ! %& & 6/ & && # % %# % & ! 2 > % & ! % && " 7 > %& 6/ / % & $ # / ! ! && & / # ! && & # % "# ! && & - " Q[ UPP % & % ! && tâÜ ñèäóÇìäÇïÜ îëçäï èêìéÇç ÖäîïìäÉñïäêè # > &' % & ! 3 ()*, dÜ<èäïäêè RNQN ô r áêççêòî ïâÜ ñèäóÇìäÇïÜ îëçäï èêìéÇç ÖäîïìäÉñïäêèL ô snH6[ 5O[ < OIL äá äï âÇî ÖÜèîäïö R 8 ü O Ñ Üôë O Hô 6I äá ô 6 áHôI ] ! O 4 X ü O Ñ Üôë â O O Hô 6Iä äá ô ^ 6[ \ ! O) Ä Pü Pü â ä òâÜìÜ Ñ ] R]95 HQ K <I NZ O O ë / snH6[ 5 [ < I. ! && / nH6[ 5OI. ! $ 6$ # &. & / nH6[ < O5OI. ! < \ Q ! "# $ < ^ Q "# < ] Q / ! ! !% " #."# / ! ! ! ! %/ &&/ & #" 3 ()*, % % && % & ! # # ! ? multivariate split normal S lÜééÇ RNQN iá snH6[ 5O[ < OI[ ïâÜè 8 eHôI ] 6 K R]95H< QI O v ÇìHôI ] É5 òâÜìÜ É ] wPO H< QIO K <N w tâÜ èÜôï çÜééÇ àäóÜî ïâÜ ñèäóÇìäÇïÜ îåÜòèÜîî e{ ô eHôI )} , ] á à ü {v ÇìHôI})GO ÇèÖ ñèäóÇìäÇïÜ åñìïêîäî e{ ô eHôI É} , ] á à O {v ÇìHôI}O êá Ç snH6[ 5O[ < OI óÇìäÇÉçÜN lÜééÇ RNRN iá ô snH6[ 5O[ < OI ïâÜè 8 , ] ÉP)GO R]9H< QI{HT]9 QIH< QIO K <} ü ÇèÖ PO ,O ] É í[ òâÜìÜ í ] SHQ K < aI]HQ K <I T9POHQ <IO HS K 9IHQ K < OI K SH9 RI< Z " # öB tâÜ èÜôï çÜééÇ àäóÜî ïâÜ éêéÜèï àÜèÜìÇïäèà áñèÑïäêè >BHïI ] eHÜ I êá Ç ñèäóÇìäÇïÜ îëçäï èêìéÇç óÇìäÇÉçÜ Çî ÖÜìäóÜÖ Éö jêâè HQYXRIN lÜééÇ RNSN iá ô snH6[ 5O[ < OIL ïâÜè 8 R5 ÜôëH 5OïO]RI(H 5ïI K < ÜôëH 5O< OïO]RI(H 5<ïI > HïI ] Z B 5HQ K <I ÜôëH6ïI ( ) SN tâÜ éñçïäóÇìäÇïÜ îëç èêìéÇç Öäîïì tâÜ áêççêòäèà ÖÜ<èäïäêè äî Ç èÇïñìÇç àÜèÜìÇçäõÇïäêè êá ïâÜ ñèäóÇìäÇïÜ îëçäï èêìéÇç ÖäîïìäÉñïäêè äè jêâè HQYXRI ïê ïâÜ éñçïäóÇìäÇïÜ îÜïïäèà ÇèÖ äî Ç ìÜëÇìÇéÜïìäõÇïäêè êá ïâÜ éñçïäóÇìäÇïÜ îëçäï èêìéÇç ÖäîïìäÉñïäêè äè gÜòÜåÜ HQYXYIN o dÜ<èäïäêè SNQN a óÜÑïêì ô r áêççêòî ïâÜ íMîëçäï èêìéÇç ÖäîïìäÉñïäêèL ô snoH6[ &[ <[ IL äá äïî ëìäèÑäëÇç ÑêéëêèÜèïî ÇRìÜ äèÖÜëÜèÖÜèïçö ÖäîïìäÉñïÜÖ Çî 8 q snHó; 6[ 5O[ < OI äá ã ó; ô 7 7 7 R q 7 8 nHó; 6[ 5OI äá ã p[ : 7 7 R q p òâÜìÜ Q[ ZZZ[ ë êá îäõÜ íL ] Q[ R[ ZZZ[ ë äî ïâÜ ÑêéëçÜéÜèï êá L ó7 äî ïâÜ ÜäàÜèóÜÑïêì ÑêììÜîëqêè2Öäáèà ïê ïâàÜ ãïâ çÇìàÜqîï ÜäàáÜèóÇçñÜ äèàèïqâÜ îëÜÑïìÇç ÖÜÑêéëêîäïäêqè êá & ] v #v ;L # ] O O ÖäÇàH5ü[ ZZZ[ 5oI ÇèÖ < ] H< 7I7jB äî Ç íMÖäéÜèîäêèÇç óÜÑïêì êá ÑêèïìÇÑïäêèOÖäçÇïäêè ëÇìÇéÜïÜìîN cêèîäÖÜì ïâÜ ÑÇîÜ ] ì áêì äççñîïìÇïäêèL äNÜN òâÜìÜ êèçö ïâÜ ìïâ ëìäèÑäëÇç ÑêéëêèÜèï âÇî Ç îåÜòÜÖ ÖäîïìäÉñïäêèqN iï áäîàïâÜè ÜÇîö ïê îÜÜ ïâÇï ïâÜ ÖÜèîäïö êá ô äî ü ; Pü ; Ñ Üôë Hô 6I & Hô 6I äá óçHô 6I P áHôI ] ! O 4 Ñ Üôë ü Hô 6I;&~ PüHô 6I äá ó; Hô 6I ^ P[ H ! ( O ) ç è ê T mattias villani and rolf larsson ρ=0.7 ρ=0 7 5 6 4 5 3 4 3 2 2 1 1 0 0 -1 -1 -4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4 fäàñìÜ QN cêèïêñì ëçêïî êá ÉäóÇìäÇïÜ QMîëçäï èêìéÇç ÖÜèîäïö áñèÑïäêèîN 6 ] H Q[ RIL & ] HQ[ :[ :[ QIL ] Q ÇèÖ < ] RN q ~ ~ ; ~ O O O O Pü ü oGO üGO òâÜìÜ & ] v #v L # ] ÖäÇàH5ü[ ZZZ[ < ü5ç[ ZZZ[ 5oI ÇèÖ Ñ ] O HR9I # HQK< üIN tâäî îâêñçÖ ÉÜ ÑêéëÇìÜÖ ïê ïâÜ ñèäóÇìäÇïÜ ÑÇîÜ äè dÜ<èäïäêè QN fäàñìÜ Q äççñîïìãÇïÜãî ïòê ëêîîäÉçÜ îâÇëÜî êá ïâÜ sn H6[ &[ <[ IMÖäîïìäÉñïäêèN O q tâÜ àÜèÜìÇç snoH6[ &[ <[ IMÖäîïìäÉñïäêè Çéêñèïî ïê ñîäèà Öä;ÜìÜèï éñçïäóÇìäÇïÜ èêìéÇç ÖäîïìäÉñïäêèîL Ççç òäïâ éêÖÜq6L êóÜì R{ ìÜàäêèî êá ro îÜëÇìÇïÜÖ Éö ïâÜ í âöëÜìëçÇèÜî ó; Hô 7 6I ] PL áêì ã N oïâÜì áêìéî êá ïâÜ îÜëÇìÇïäèà âöëÜìëçÇèÜîL êì éêìÜ àÜèÜìÇç ÑâÇèàÜî äè ÑêóÇìäÇèÑÜ îïìñRÑïqñìÜ ÉÜïòÜÜè ïâÜ R{ ìÜàäêèîL ëìêÖñÑÜ äççMÉÜâÇóÜÖ ÖÜèîäïäÜî òäïâ îâÇìë ìäÖàÜîN tâÜ èêìéÇç ÇèÖ îëçäï èêìéÇç ÖäîïìäÉñïäêèî äè dÜ<èäïäêè SNQ éÇö êÉóäêñîçö ÉÜ ìÜëçÇÑÜÖ Éö êïâÜì ÖäîïìäÉñïäêè $ NàN ï ! (0#"$ )*), çê#à ìÜ % && snoH6[ &[ <[ I ! . wPO O q # $ É7 ] w H< 7 QI K < 7 ã > ' % R q tâÜêìÜé SNQN iá ô sn H6[ &[ <[ IL ïâÜè 8 o q eHôI ] 6 K R]9 57H< 7 QIó- B x v ÇìHôI ] v #üv ; òâÜìÜ #ü äî Ç ÖäÇàêèÇç éÇïìäô òäïâ äïâ ÜçÜéÜèï ÜíñÇç ïê 5O äá ã p êì É 5O äá ã N 7 R q 7 7 R q m ] Hô éI;sPüHõ éI[ BR ! èêÉä !# # ë. & / ! % ô õ$ # é s % $ . &%/ ()1;, mBR > #/ éñçïäóÇìäÇïÜ îåÜòèÜîî ) ,üÅo ] eHmBRIZ ô noH6[ &I$ ,üÅo ] P ,üÅo % "# 8 O ?/ ,üÅü ] ,ü ! / ! > éñçïäóÇìäÇïÜ åñìïêîäî ($ )1;, O ,OÅo ] eHmBBIZ multivariate split normal U iá noH6[ &IL ïâÜè ,OÅo ] ëHë K RIN nêïÜ Ççîê ïâÇï ,OÅü ] ,ON tâÜ áêççêòäèà ìÜîñçï äî ïâÜ éñçï8äóÇìäÇïÜ ÜôïÜèîäêè êá lÜééÇ RNRN tâÜêìÜé SNRN iá ô snH6[ &[ <[ I ïâÜè 8 q P) O O O ,üÅo ] É7 HR]9IH< 7 QI {HT]9 QIH< 7 QI K < 7} B x PO ,OÅo ] ëHë K RI K É7 í7 Sí[ B x a PO O O òâÜìÜ í7 ] SHQ K < 7 I]HQ K < 7I T9 HQ < 7I HS K 9IHQ K < 7 I K SH9 RI< 7 Z â ; ä tâÜ éêéÜèï àÜèÜìÇïäèà áñèÑïäêè >BHïI ] e{ÜôëHï ôI} êá Ç snoH6[ &[ <[ I óÇìäÇÉçÜ äî àäóÜè äè ïâÜ èÜôï ìÜîñçïN q tâÜêìÜé SNSN iá ô sn H6[ &[ <[ IL ïâÜè 8 o q ; O ; ; O ; R5- Üôë{ H57ó7ïI ]R}(H 57ó7ïI K < 7 Üôë{ H57< 7ó7ïI ]R}(H 57< 7ó7ïI >BHïI ] ; R è 57HQ K < 7I ÜôëH6 ó ïI êS B 7 7 y T Q U Üôë {6 ó; ï Hó; ïIO5O} Z " 7 7 R 7 7 H Bp I x TN mÇôäéñé çäåÜçäâêêÖ Üîï éÇï bÜáêìÜ ÜéÉÇìåäèà êè ïâÜ éñçïäóÇìäÇïÜ ÑÇîÜ òÜ àäóÜ Ç ñîÜáñç çÜééÇ ÑêèÑÜìèäèà éÇôäéñé çäåÜçäâêêÖ ÜîïäéÇïäêè äè ïâÜ ñèäóÇìäÇïÜ îÜïïäèàN O O lÜééÇ TNQN gäóÜè Ç ìÇèÖêé îÇéëçÜ ôü[ ZZZ[ ô\ áìêé snH6[ 5 [ < IL ïâÜ çäåÜçäâêêÖL éÇôäéäõÜÖ êóÜì 5 ÇèÖ <L äî Rè \GO l H6I ] à H6IP)\GO [ 9Ü 2 3 òâÜìÜ É üG) üG) à H6I ] îü K îO [ O îü ] Hô- 6I [ m x O îO ] Hô- 6I [ mp x p òâÜìÜ ] ä ] Q[ ZZZ[ è Z Hô- 6I P ÇèÖ ] ä ] Q[ ZZZ[ è Z Hô- 6I ^ P N mêìÜêóÜìL ïâÜ éÇôäéiñé çäáåÜçäâêêÖ ÜîïäéÇïê ìî êá 45O ÇàèÖ < ÇiìÜ á à OG) O î à H6I 5 ] ü [ è îüG) É< ] O Z üG) îü wÜ èêò ïñìè ïê éÇôäéñé çäåÜçäâêêÉÖ ÜîïäéÇïäêè äè ïâÜ éñçïäóÇìäÇïÜ ÑÇîÜN iï äî ëêîîäÉçÜ ïê éÇôäéäõÜ ïâÜ çäåÜçäâêêÖ ÇèÇçöïäÑÇççö òNìNïN # ÇèÖ <N tâÜ ìÜîñçï äî àäóÜè äè ïâÜ áêççêòäèà ïâÜêìÜéN - mattias villani and rolf larsson tâÜêìÜé TNQN è Ç ìÇèÖ é îÇéëçÜ êá óÜÑï ü[ ZZZ[ ô\ sn H6[ &[ <[ IL òâÜìÜ & ] v #v ;L ïâÜ çäåÜçäâêêÖL éÇôäéäõÜÖ òNìNïN # ÇèÖ < äî q Rb{PoGO9\è{\GO l H6[ v[ I ] 5 H6[ v IP\ à H6[ v IP)\GO [ q o\GO 7 7 H9ÜI 7jBp 7jB y y òâÜìÜ É É üG) üG) à7 H6[ v I ] îü7 K îO7 [ ; O ; ; O òâÜìÜ îü7 ] {ó Hô- 6I} [ 7 ] ä ] Q[ ZZZ[ è Z ó Hô- 6I P L îO7 ] p {ó Hô- 6I} L m7 7 i á 7 4 à m7 7 p ] ä ] Q[ ZZZ[ è Z ó; Hô 6I ^ P [ ÇèÖ ïâÜ éÇôäéñé çäåÜçäâêêÖ ÜîïäéÇïêìî êá 5O ÇèÖ < ÇìÜ i7 á p 7 - à p 7 7 OG) O ü î à H6[ v I äá ã [ 5 H6[ v I ] \ ü7 7 R q 7 ü \ {ó; Hô 6I}O äá ã p[ H \ -Dü 7 - R q ÇèÖ É p î üG) < H6[ v I ] O7 Z 7 î 2 ü7 3 wÜ éÇö ñîÜ ïâäî ïâÜêìÜé áêì èñéÜìäÑÇç éÇôäéäõÇïäêè êá ïâÜ çäåÜçäâêêÖ òNìNïN 6 ÇèÖ v L áêì Ç àäóÜè N iè ïâÜ ïòêMÖäéÜèîäêèÇç ÑÉÇîÜL v éÇö ÉÜ ÜôëçäÑäïçö ëÇìÇéÜïìäõÜÖ Çî q Ñêî 2 îäè 2 9 9 HTNQI v ] [ \ 2 Z îäè 2 Ñêî 2 R 4 R 2 3 a îäéäçÇì ëÇìÇéÜïìäõÇïäêè êá v äî ÇóÇäçÇÉçÜ äè ïâÜ àÜèÜìÇç ÑÇîÜ ñîäèà eñçÜìäÇè ÇèàçÜî HkâÇM ïìä ÇèÖ mÇìÖäÇL QYWWIN hÜèÑÜL éÇôäéäõÇïäêè êóÜì v ÇèÖ 6 äî îïìÇäàâïáêìòÇìÖçö ëÜìáêìéÜÖ òäïâ îïÇèÖÇìÖ èñéÜìäÑÇç êëïäéäõÇïäêè ÇçàêìäïâéîN açïÜìèÇïäóÜçöL eÖÜçéÇèL aìäÇî ÇèÖ séäïâ HQYYXI âÇóÜ ÖÜóÜçêëÜÖ êëïäéäõÇïäêè Ççàêìäïâéî êè ïâÜ sïäÜáÜç éÇèäáêçÖ HïâÜ îÜï êá êìïâêèêìéÇç éÇïìäÑÜîI òâäÑâ ÇóêäÖ Çè ÜôëçäÑäï ëÇìÇéÜïìäõÇïäêè êá v N UN bÇöÜîäÇè äèáÜìÜèÑÜ lÜï ôü[ ZZZ[ ô\ ÉÜ Ç ìÇèÖêé îÇéëçÜ áìêé snoH6[ &[ <[ IN tâÜ ãêäèï ëêîïÜìäêì ÖäîïìäÉñïäêè êá Ççç ëÇìÇéÜïÜìî éÇö ÉÜ òìäïïÜè Çî q ëH6[ v[ 5[ <[ [ í
Load more

Recommended publications
  • 5. the Student T Distribution
    Virtual Laboratories > 4. Special Distributions > 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5. The Student t Distribution In this section we will study a distribution that has special importance in statistics. In particular, this distribution will arise in the study of a standardized version of the sample mean when the underlying distribution is normal. The Probability Density Function Suppose that Z has the standard normal distribution, V has the chi-squared distribution with n degrees of freedom, and that Z and V are independent. Let Z T= √V/n In the following exercise, you will show that T has probability density function given by −(n +1) /2 Γ((n + 1) / 2) t2 f(t)= 1 + , t∈ℝ ( n ) √n π Γ(n / 2) 1. Show that T has the given probability density function by using the following steps. n a. Show first that the conditional distribution of T given V=v is normal with mean 0 a nd variance v . b. Use (a) to find the joint probability density function of (T,V). c. Integrate the joint probability density function in (b) with respect to v to find the probability density function of T. The distribution of T is known as the Student t distribution with n degree of freedom. The distribution is well defined for any n > 0, but in practice, only positive integer values of n are of interest. This distribution was first studied by William Gosset, who published under the pseudonym Student. In addition to supplying the proof, Exercise 1 provides a good way of thinking of the t distribution: the t distribution arises when the variance of a mean 0 normal distribution is randomized in a certain way.
    [Show full text]
  • Chapter 8 Fundamental Sampling Distributions And
    CHAPTER 8 FUNDAMENTAL SAMPLING DISTRIBUTIONS AND DATA DESCRIPTIONS 8.1 Random Sampling pling procedure, it is desirable to choose a random sample in the sense that the observations are made The basic idea of the statistical inference is that we independently and at random. are allowed to draw inferences or conclusions about a Random Sample population based on the statistics computed from the sample data so that we could infer something about Let X1;X2;:::;Xn be n independent random variables, the parameters and obtain more information about the each having the same probability distribution f (x). population. Thus we must make sure that the samples Define X1;X2;:::;Xn to be a random sample of size must be good representatives of the population and n from the population f (x) and write its joint proba- pay attention on the sampling bias and variability to bility distribution as ensure the validity of statistical inference. f (x1;x2;:::;xn) = f (x1) f (x2) f (xn): ··· 8.2 Some Important Statistics It is important to measure the center and the variabil- ity of the population. For the purpose of the inference, we study the following measures regarding to the cen- ter and the variability. 8.2.1 Location Measures of a Sample The most commonly used statistics for measuring the center of a set of data, arranged in order of mag- nitude, are the sample mean, sample median, and sample mode. Let X1;X2;:::;Xn represent n random variables. Sample Mean To calculate the average, or mean, add all values, then Bias divide by the number of individuals.
    [Show full text]
  • Chapter 4: Central Tendency and Dispersion
    Central Tendency and Dispersion 4 In this chapter, you can learn • how the values of the cases on a single variable can be summarized using measures of central tendency and measures of dispersion; • how the central tendency can be described using statistics such as the mode, median, and mean; • how the dispersion of scores on a variable can be described using statistics such as a percent distribution, minimum, maximum, range, and standard deviation along with a few others; and • how a variable’s level of measurement determines what measures of central tendency and dispersion to use. Schooling, Politics, and Life After Death Once again, we will use some questions about 1980 GSS young adults as opportunities to explain and demonstrate the statistics introduced in the chapter: • Among the 1980 GSS young adults, are there both believers and nonbelievers in a life after death? Which is the more common view? • On a seven-attribute political party allegiance variable anchored at one end by “strong Democrat” and at the other by “strong Republican,” what was the most Democratic attribute used by any of the 1980 GSS young adults? The most Republican attribute? If we put all 1980 95 96 PART II :: DESCRIPTIVE STATISTICS GSS young adults in order from the strongest Democrat to the strongest Republican, what is the political party affiliation of the person in the middle? • What was the average number of years of schooling completed at the time of the survey by 1980 GSS young adults? Were most of these twentysomethings pretty close to the average on
    [Show full text]
  • Notes Mean, Median, Mode & Range
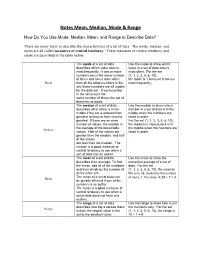
    Notes Mean, Median, Mode & Range How Do You Use Mode, Median, Mean, and Range to Describe Data? There are many ways to describe the characteristics of a set of data. The mode, median, and mean are all called measures of central tendency. These measures of central tendency and range are described in the table below. The mode of a set of data Use the mode to show which describes which value occurs value in a set of data occurs most frequently. If two or more most often. For the set numbers occur the same number {1, 1, 2, 3, 5, 6, 10}, of times and occur more often the mode is 1 because it occurs Mode than all the other numbers in the most frequently. set, those numbers are all modes for the data set. If each number in the set occurs the same number of times, the set of data has no mode. The median of a set of data Use the median to show which describes what value is in the number in a set of data is in the middle if the set is ordered from middle when the numbers are greatest to least or from least to listed in order. greatest. If there are an even For the set {1, 1, 2, 3, 5, 6, 10}, number of values, the median is the median is 3 because it is in the average of the two middle the middle when the numbers are Median values. Half of the values are listed in order. greater than the median, and half of the values are less than the median.
    [Show full text]
  • Volatility Modeling Using the Student's T Distribution
    Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Economics Aris Spanos, Chair Richard Ashley Raman Kumar Anya McGuirk Dennis Yang August 29, 2003 Blacksburg, Virginia Keywords: Student’s t Distribution, Multivariate GARCH, VAR, Exchange Rates Copyright 2003, Maria S. Heracleous Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous (ABSTRACT) Over the last twenty years or so the Dynamic Volatility literature has produced a wealth of uni- variateandmultivariateGARCHtypemodels.Whiletheunivariatemodelshavebeenrelatively successful in empirical studies, they suffer from a number of weaknesses, such as unverifiable param- eter restrictions, existence of moment conditions and the retention of Normality. These problems are naturally more acute in the multivariate GARCH type models, which in addition have the problem of overparameterization. This dissertation uses the Student’s t distribution and follows the Probabilistic Reduction (PR) methodology to modify and extend the univariate and multivariate volatility models viewed as alternative to the GARCH models. Its most important advantage is that it gives rise to internally consistent statistical models that do not require ad hoc parameter restrictions unlike the GARCH formulations. Chapters 1 and 2 provide an overview of my dissertation and recent developments in the volatil- ity literature. In Chapter 3 we provide an empirical illustration of the PR approach for modeling univariate volatility. Estimation results suggest that the Student’s t AR model is a parsimonious and statistically adequate representation of exchange rate returns and Dow Jones returns data.
    [Show full text]
  • The Value at the Mode in Multivariate T Distributions: a Curiosity Or Not?
    The value at the mode in multivariate t distributions: a curiosity or not? Christophe Ley and Anouk Neven Universit´eLibre de Bruxelles, ECARES and D´epartement de Math´ematique,Campus Plaine, boulevard du Triomphe, CP210, B-1050, Brussels, Belgium Universit´edu Luxembourg, UR en math´ematiques,Campus Kirchberg, 6, rue Richard Coudenhove-Kalergi, L-1359, Luxembourg, Grand-Duchy of Luxembourg e-mail: [email protected]; [email protected] Abstract: It is a well-known fact that multivariate Student t distributions converge to multivariate Gaussian distributions as the number of degrees of freedom ν tends to infinity, irrespective of the dimension k ≥ 1. In particular, the Student's value at the mode (that is, the normalizing ν+k Γ( 2 ) constant obtained by evaluating the density at the center) cν;k = k=2 ν converges towards (πν) Γ( 2 ) the Gaussian value at the mode c = 1 . In this note, we prove a curious fact: c tends k (2π)k=2 ν;k monotonically to ck for each k, but the monotonicity changes from increasing in dimension k = 1 to decreasing in dimensions k ≥ 3 whilst being constant in dimension k = 2. A brief discussion raises the question whether this a priori curious finding is a curiosity, in fine. AMS 2000 subject classifications: Primary 62E10; secondary 60E05. Keywords and phrases: Gamma function, Gaussian distribution, value at the mode, Student t distribution, tail weight. 1. Foreword. One of the first things we learn about Student t distributions is the fact that, when the degrees of freedom ν tend to infinity, we retrieve the Gaussian distribution, which has the lightest tails in the Student family of distributions.
    [Show full text]
  • Statistics, Measures of Central Tendency I
    Statistics, Measures of Central TendencyI We are considering a random variable X with a probability distribution which has some parameters. We want to get an idea what these parameters are. We perfom an experiment n times and record the outcome. This means we have X1;:::; Xn i.i.d. random variables, with probability distribution same as X . We want to use the outcome to infer what the parameters are. Mean The outcomes are x1;:::; xn. The Sample Mean is x1+···+xn x := n . Also sometimes called the average. The expected value of X , EX , is also called the mean of X . Often denoted by µ. Sometimes called population mean. Median The number so that half the values are below, half above. If the sample is of even size, you take the average of the middle terms. Mode The number that occurs most frequently. There could be several modes, or no mode. Dan Barbasch Math 1105 Chapter 9 Week of September 25 1 / 24 Statistics, Measures of Central TendencyII Example You have a coin for which you know that P(H) = p and P(T ) = 1 − p: You would like to estimate p. You toss it n times. You count the number of heads. The sample mean should be an estimate of p: EX = p, and E(X1 + ··· + Xn) = np: So X + ··· + X E 1 n = p: n Dan Barbasch Math 1105 Chapter 9 Week of September 25 2 / 24 Descriptive StatisticsI Frequency Distribution Divide into a number of equal disjoint intervals. For each interval count the number of elements in the sample occuring.
    [Show full text]
  • Exploring the Mode – the Most Likely Value? Jerzy Letkowski Western New England University
    OC13077 Exploring the Mode – the Most Likely Value? Jerzy Letkowski Western New England University Abstract The mean, median and mode are typical summary measures, each representing some focal tendency in random data. Even so the focus of each of the measures is different; they usually are packaged together as measures of central tendency. Among these three measures, the mode is granted the least amount of attention and it is frequently misinterpreted in many introductory textbooks on statistics. Also its centrality is questionable in some situations. The purpose of the paper is to provide a formal definition of the mode and to show appropriate interpretation of this measure with respect to different random data types: qualitative and quantitative (discrete and continuous). Several cases are presented to exemplify this purpose. Detail data processing steps are shown in Google spreadsheets. Keywords: mode, statistics, summary measures, probability distribution, data types, spreadsheet. Exploring the Mode – the Most Likely Value? OC13077 WHAT IS THE MODE? In general, in the context of a population, the concept of the mode of a random variable, X, having domain DX, is quite simple. Formally speaking (Spiegel, 1975, p. 84, McClave, 2011, p. 58, Sharpie, 2010, p. 115), it is a value, x*, of the variable that uniquely maximizes the probability-distribution function, f(x) : x* : f (x* ) = max {f (x)} or None (i) x∈DX One could refer to such a definition of the mode as a probability-distribution driven definition. In a way, it is a universal definition. For example, the maximum point for the Normal distribution (density function) is µ.
    [Show full text]
  • UNIT NUMBER 19.4 PROBABILITY 4 (Measures of Location and Dispersion)
    “JUST THE MATHS” UNIT NUMBER 19.4 PROBABILITY 4 (Measures of location and dispersion) by A.J.Hobson 19.4.1 Common types of measure 19.4.2 Exercises 19.4.3 Answers to exercises UNIT 19.4 - PROBABILITY 4 MEASURES OF LOCATION AND DISPERSION 19.4.1 COMMON TYPES OF MEASURE We include, here three common measures of location (or central tendency), and one common measure of dispersion (or scatter), used in the discussion of probability distributions. (a) The Mean (i) For Discrete Random Variables If the values x1, x2, x3, . , xn of a discrete random variable, x, have probabilities P1,P2,P3,....,Pn, respectively, then Pi represents the expected frequency of xi divided by the total number of possible outcomes. For example, if the probability of a certain value of x is 0.25, then there is a one in four chance of its occurring. The arithmetic mean, µ, of the distribution may therefore be given by the formula n X µ = xiPi. i=1 (ii) For Continuous Random Variables In this case, it is necessary to use the probability density function, f(x), for the distribution which is the rate of increase of the probability distribution function, F (x). For a small interval, δx of x-values, the probability that any of these values occurs is ap- proximately f(x)δx, which leads to the formula Z ∞ µ = xf(x) dx. −∞ (b) The Median (i) For Discrete Random Variables The median provides an estimate of the middle value of x, taking into account the frequency at which each value occurs.
    [Show full text]
  • Skewness and Kurtosis 2
    A distribution is said to be 'skewed' when the mean and the median fall at different points in the distribution, and the balance (or centre of gravity) is shifted to one side or the other-to left or right. Measures of skewness tell us the direction and the extent of Skewness. In symmetrical distribution the mean, median and mode are identical. The more the mean moves away from the mode, the larger the asymmetry or skewness A frequency distribution is said to be symmetrical if the frequencies are equally distributed on both the sides of central value. A symmetrical distribution may be either bell – shaped or U shaped. 1- Bell – shaped or unimodel Symmetrical Distribution A symmetrical distribution is bell – shaped if the frequencies are first steadily rise and then steadily fall. There is only one mode and the values of mean, median and mode are equal. Mean = Median = Mode A frequency distribution is said to be skewed if the frequencies are not equally distributed on both the sides of the central value. A skewed distribution may be • Positively Skewed • Negatively Skewed • ‘L’ shaped positively skewed • ‘J’ shaped negatively skewed Positively skewed Mean ˃ Median ˃ Mode Negatively skewed Mean ˂ Median ˂ Mode ‘L’ Shaped Positively skewed Mean ˂ Mode Mean ˂ Median ‘J’ Shaped Negatively Skewed Mean ˃ Mode Mean ˃ Median In order to ascertain whether a distribution is skewed or not the following tests may be applied. Skewness is present if: The values of mean, median and mode do not coincide. When the data are plotted on a graph they do not give the normal bell shaped form i.e.
    [Show full text]
  • Measures of Central Tendency & Dispersion
    Measures of Central Tendency & Dispersion Measures that indicate the approximate center of a distribution are called measures of central tendency. Measures that describe the spread of the data are measures of dispersion. These measures include the mean, median, mode, range, upper and lower quartiles, variance, and standard deviation. A. Finding the Mean The mean of a set of data is the sum of all values in a data set divided by the number of values in the set. It is also often referred to as an arithmetic average. The Greek letter (“mu”) is used as the symbol for population mean and the symbol ̅ is used to represent the mean of a sample. To determine the mean of a data set: 1. Add together all of the data values. 2. Divide the sum from Step 1 by the number of data values in the set. Formula: ∑ Example: Consider the data set: 17, 10, 9, 14, 13, 17, 12, 20, 14 ∑ The mean of this data set is 14. B. Finding the Median The median of a set of data is the “middle element” when the data is arranged in ascending order. To determine the median: 1. Put the data in order from smallest to largest. 2. Determine the number in the exact center. i. If there are an odd number of data points, the median will be the number in the absolute middle. ii. If there is an even number of data points, the median is the mean of the two center data points, meaning the two center values should be added together and divided by 2.
    [Show full text]
  • Fluorescence Correlation Spectroscopy 1
    Petra Schwille and Elke Haustein Fluorescence Correlation Spectroscopy 1 Fluorescence Correlation Spectroscopy An Introduction to its Concepts and Applications Petra Schwille and Elke Haustein Experimental Biophysics Group Max-Planck-Institute for Biophysical Chemistry Am Fassberg 11 D-37077 Göttingen Germany 2 Fluorescence Correlation Spectroscopy Petra Schwille and Elke Haustein Table of Contents TABLE OF CONTENTS 1 1. INTRODUCTION 3 2. EXPERIMENTAL REALIZATION 5 2.1. ONE-PHOTON EXCITATION 5 2.2. TWO-PHOTON EXCITATION 7 2.3. FLUORESCENT DYES 9 3. THEORETICAL CONCEPTS 10 3.1. AUTOCORRELATION ANALYSIS 10 3.2. CROSS-CORRELATION ANALYSIS 18 4. FCS APPLICATIONS 21 4.1. CONCENTRATION AND AGGREGATION MEASUREMENTS 21 4.2. CONSIDERATION OF RESIDENCE TIMES: DETERMINING MOBILITY AND MOLECULAR INTERACTIONS 23 4.2.1 DIFFUSION ANALYSIS 23 4.2.2 CONFINED AND ANOMALOUS DIFFUSION 24 4.2.3 ACTIVE TRANSPORT PHENOMENA IN TUBULAR STRUCTURES 24 4.2.4 DETERMINATION OF MOLECULAR INTERACTIONS 26 4.2.5 CONFORMATIONAL CHANGES 27 4.3. CONSIDERATION OF CROSS-CORRELATION AMPLITUDES: A DIRECT WAY TO MONITOR ASSOCIATION/DISSOCIATION AND ENZYME KINETICS 28 4.4. CONSIDERATION OF FAST FLICKERING: INTRAMOLECULAR DYNAMICS AND PROBING OF THE MICROENVIRONMENT 30 5. CONCLUSIONS AND OUTLOOK 31 6. REFERENCES 32 Petra Schwille and Elke Haustein Fluorescence Correlation Spectroscopy 3 1. Introduction Currently, it is almost impossible to open your daily newspaper without stumbling over words like gene manipulation, genetic engineering, cloning, etc. that reflect the tremendous impact of life sciences to our modern world. Press coverage of these features has long left behind the stage of merely reporting scientific facts. Instead, it focuses on general pros and cons, and expresses worries about what scientists have to do and what to refrain from.
    [Show full text]