DOCSLIB.ORG

Probability Distributions CEE 201L

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Probability Distributions CEE 201L Probability Distributions CEE 201L. Uncertainty, Design, and Optimization Department of Civil and Environmental Engineering Duke University Philip Scott Harvey, Henri P. Gavin and Jeffrey T. Scruggs Spring 2022 1 Probability Distributions Consider a continuous, random variable (rv) X with support over the domain X . The probability density function (PDF) of X is the function fX (x) such that for any two numbers a and b in the domain X , with a < b, Z b P [a < X ≤ b] = fX (x) dx a For fX (x) to be a proper distribution, it must satisfy the following two conditions: 1. The PDF fX (x) is positive-valued; fX (x) ≥ 0 for all values of x ∈ X . R 2. The rule of total probability holds; the total area under fX (x) is 1; X fX (x) dx = 1. Alternately, X may be described by its cumulative distribution function (CDF). The CDF of X is the function FX (x) that gives, for any specified number x ∈ X , the probability that the random variable X is less than or equal to the number x is written as P [X ≤ x]. For real values of x, the CDF is defined by Z b FX (x) = P [X ≤ b] = fX (x) dx , −∞ so, P [a < X ≤ b] = FX (b) − FX (a) By the first fundamental theorem of calculus, the functions fX (x) and FX (x) are related as d f (x) = F (x) X dx X 2 CEE 201L. Uncertainty, Design, and Optimization – Duke University – Spring 2022 – P.S.H., H.P.G. and J.T.S. A few important characteristics of CDF’s of X are: 1. CDF’s, FX (x), are monotonic non-decreasing functions of x. 2. For any number a, P [X > a] = 1 − P [X ≤ a] = 1 − FX (a) R b 3. For any two numbers a and b with a < b, P [a < X ≤ b] = FX (b) − FX (a) = a fX (x)dx 2 Descriptors of random variables The expected or mean value of a continuous random variable X with PDF fX (x) is the centroid of the probability density. Z ∞ µX = E[X] = x fX (x) dx −∞ The expected value of an arbitrary function of X, g(X), with respect to the PDF fX (x) is Z ∞ µg(X) = E[g(X)] = g(x) fX (x) dx −∞ The variance of a continuous rv X with PDF fX (x) and mean µX gives a quantitative measure of how much spread or dispersion there is in the distribution of x values. The variance is calculated as Z ∞ 2 2 σX = V[X] = (x − µX ) fX (x) dx −∞ = = = = p The standard deviation (s.d.) of X is σX = V[X]. The coefficient of variation (c.o.v.) of X is defined as the ratio of the standard deviation σX to the mean µX : σX cX = µX for non-zero mean. The c.o.v. is a normalized measure of dispersion (dimensionless). A mode of a probability density function, fX (x), is a value of x such that the PDF is maximized; d fX (x) = 0 . dx x=xmode The median value, xm, is is the value of x such that P [X ≤ xm] = P [X > xm] = FX (xm) = 1 − FX (xm) = 0.5 . CC BY-NC-ND March 25, 2021 PSH, HPG, JTS Probability Distributions 3 3 Some common distributions The National Institute of Standards and Technology (NIST) lists properties of nineteen commonly used probability distributions in their Engineering Statistics Handbook. This section describes the properties of seven distributions. For each of these distributions, this document provides figures and equations for the PDF and CDF, equations for the mean and variance, the names of Matlab functions to generate samples, and empirical distributions of such samples. 3.1 The Normal distribution The Normal (or Gaussian) distribution is perhaps the most commonly used distribution function. 2 The notation X ∼ N (µX , σX ) denotes that X is a normal random variable with mean µX and 2 variance σX . The standard normal random variable, Z, or “z-statistic”, is distributed as N (0, 1). The probability density function of a standard normal random variable is so widely used it has its own special symbol, φ(z), ! 1 z2 φ(z) = √ exp − 2π 2 Any normally distributed random variable can be defined in terms of the standard normal random variable, through the change of variables X = µX + σX Z. If X is normally distributed, it has the PDF 2 ! x − µX 1 (x − µX ) fX (x) = φ = q exp − 2 σX 2 2σ 2πσX X There is no closed-form equation for the CDF of a normal random variable. Solving the integral z 1 Z 2 Φ(z) = √ e−u /2 du 2π −∞ would make you famous. Try it. The CDF of a normal random variable is expressed in terms of the error function, erf(z). If X is normally distributed, P [X ≤ x] can be found from the standard normal CDF x − µX P [X ≤ x] = FX (x) = Φ . σX Values for Φ(z) are tabulated and can be computed, e.g., the Matlab command . Prob_X_le_x = normcdf(x,muX,sigX). The standard normal PDF is symmetric about z = 0, so φ(−z) = φ(z), Φ(−z) = 1 − Φ(z), and P [X > x] = 1 − FX (x) = 1 − Φ ((x − µX )/σX ) = Φ ((µX − x)/σX ). The linear combination of two independent normal rv’s X1 and X2 (with means µ1 and µ2 and 2 2 variances σ1 and σ2) is also normally distributed, 2 2 2 2 aX1 + bX2 ∼ N aµ1 + bµ2, a σ1 + b σ2 , 2 2 and more specifically, aX − b ∼ N aµX − b, a σX . CC BY-NC-ND March 25, 2021 PSH, HPG, JTS 4 CEE 201L. Uncertainty, Design, and Optimization – Duke University – Spring 2022 – P.S.H., H.P.G. and J.T.S. Given the probability of a normal rv, i.e., given P [X ≤ x], the associated value of x can be found from the inverse standard normal CDF, x − µ X = z = Φ−1(P [X ≤ x]) . σX Values of the inverse standard normal CDF are tabulated, and can be computed, e.g., the Matlab command . x = norminv(Prob_X_le_x,muX,sigX). 3.2 The Log-Normal distribution The Normal distribution is symmetric and can be used to describe random variables that can take positive as well as negative values, regardless of the value of the mean and standard deviation. For many random quantities a negative value makes no sense (e.g., modulus of elasticity, air pressure, and distance). Using a distribution which admits only positive values for such quantities eliminates any possibility of non-sensical negative values. The log-normal distribution is such a distribution. If ln X is normally distributed (i.e., ln X ∼ N (µln X , σln X )) then X is called a log-normal random variable. In other words, if Y (= ln X) is normally distributed, eY (= X) is log-normally distributed. P [Y ≤ y] FY (y) Φ y−µY 2 2 σY µY = µln X , σY = σln X , P [ln X ≤ ln x] = Fln X (ln x) = Φ ln x−µln X P [X ≤ x] FX (x) σln X The mean and standard deviation of a log-normal variable X are related to the mean and standard deviation of ln X. 1 µ = ln µ − σ2 σ2 = ln 1 + (σ /µ )2 ln X X 2 ln X ln X X X If (σX /µX ) < 0.30, σln X ≈ (σX /µX ) = cX The median, xm, is a useful parameter of log-normal rv’s. By definition of the median value, half of the population lies above the median, and half lies below, so ln x − µ Φ m ln X = 0.5 σln X ln x − µ m ln X = Φ−1(0.5) = 0 σln X q 2 and, ln xm = µln X ↔ xm = exp(µln X ) ↔ µX = xm 1 + cX For the log-normal distribution xmode < xmedian < xmean. If cX < 0.15, xmedian ≈ xmean. If ln X is normally distributed (X is log-normal) then (for cX < 0.3) ln x − ln x P [X ≤ x] ≈ Φ m cX 2 2 n m If ln X ∼ N (µln X , σln X ), and ln Y ∼ N (µln Y , σln Y ), and Z = aX /Y then 2 ln Z = ln a + n ln X − m ln Y ∼ N (µln Z , σln Z ) where µln Z = ln a + nµln X − mµln Y = ln a + n ln xm − m ln ym 2 2 2 2 2 2 2 2 and σln Z = (nσln X ) + (mσln Y ) = n ln(1 + cX ) + m ln(1 + cY ) = ln(1 + cZ ) CC BY-NC-ND March 25, 2021 PSH, HPG, JTS Probability Distributions 5 Uniform X ∼ U[a, b] Triangular X ∼ T (a, b, c) a ≤ X ≤ b; a ≤ X ≤ b, a ≤ c ≤ b 1/(b-a) 2/(b-a) p.d.f., f(x) p.d.f., f(x) 0 0 a µ-σ µ µ+ σ b a µ-σc µ µ+ σ µ+2 σ b 0.97 0.79 0.82 0.5 0.55 c.d.f., F(x) c.d.f., F(x) 0.21 0.17 a µ-σ µ µ+ σ b a µ-σc µ µ+ σ µ+2 σ b x x 2(x−a) ( , x ∈ [a, c] 1 , x ∈ [a, b] (b−a)(c−a) f(x) = b−a f(x) = 2(b−x) , x ∈ [c, b] 0, otherwise (b−a)(b−c) 0, otherwise 0, x ≤ a 2 0, x ≤ a (x−a) x−a (b−a)(c−a) , x ∈ [a, c] F (x) = b−a , x ∈ [a, b] F (x) = (b−x)2 1 − , x ∈ [c, b] 1, x ≥ b (b−a)(b−c) 1, x ≥ b 1 1 µX = 2 (a + b) µX = 3 (a + b + c) 2 1 2 2 1 2 2 2 σX = 12 (b − a) σX = 18 (a + b + c − ab − ac − bc) x = a + (b-a)*rand(1,N); x = triangular rnd(a,b,c,1,N); 0.8 0.8 0.6 0.6 0.4 0.4 empirical p.d.f.
Load more

Recommended publications
  • Applied Biostatistics Mean and Standard Deviation the Mean the Median Is Not the Only Measure of Central Value for a Distribution
    Health Sciences M.Sc. Programme Applied Biostatistics Mean and Standard Deviation The mean The median is not the only measure of central value for a distribution. Another is the arithmetic mean or average, usually referred to simply as the mean. This is found by taking the sum of the observations and dividing by their number. The mean is often denoted by a little bar over the symbol for the variable, e.g. x . The sample mean has much nicer mathematical properties than the median and is thus more useful for the comparison methods described later. The median is a very useful descriptive statistic, but not much used for other purposes. Median, mean and skewness The sum of the 57 FEV1s is 231.51 and hence the mean is 231.51/57 = 4.06. This is very close to the median, 4.1, so the median is within 1% of the mean. This is not so for the triglyceride data. The median triglyceride is 0.46 but the mean is 0.51, which is higher. The median is 10% away from the mean. If the distribution is symmetrical the sample mean and median will be about the same, but in a skew distribution they will not. If the distribution is skew to the right, as for serum triglyceride, the mean will be greater, if it is skew to the left the median will be greater. This is because the values in the tails affect the mean but not the median. Figure 1 shows the positions of the mean and median on the histogram of triglyceride.
    [Show full text]
  • TR Multivariate Conditional Median Estimation
    Discussion Paper: 2004/02 TR multivariate conditional median estimation Jan G. de Gooijer and Ali Gannoun www.fee.uva.nl/ke/UvA-Econometrics Department of Quantitative Economics Faculty of Economics and Econometrics Universiteit van Amsterdam Roetersstraat 11 1018 WB AMSTERDAM The Netherlands TR Multivariate Conditional Median Estimation Jan G. De Gooijer1 and Ali Gannoun2 1 Department of Quantitative Economics University of Amsterdam Roetersstraat 11, 1018 WB Amsterdam, The Netherlands Telephone: +31—20—525 4244; Fax: +31—20—525 4349 e-mail: [email protected] 2 Laboratoire de Probabilit´es et Statistique Universit´e Montpellier II Place Eug`ene Bataillon, 34095 Montpellier C´edex 5, France Telephone: +33-4-67-14-3578; Fax: +33-4-67-14-4974 e-mail: [email protected] Abstract An affine equivariant version of the nonparametric spatial conditional median (SCM) is con- structed, using an adaptive transformation-retransformation (TR) procedure. The relative performance of SCM estimates, computed with and without applying the TR—procedure, are compared through simulation. Also included is the vector of coordinate conditional, kernel- based, medians (VCCMs). The methodology is illustrated via an empirical data set. It is shown that the TR—SCM estimator is more efficient than the SCM estimator, even when the amount of contamination in the data set is as high as 25%. The TR—VCCM- and VCCM estimators lack efficiency, and consequently should not be used in practice. Key Words: Spatial conditional median; kernel; retransformation; robust; transformation. 1 Introduction p s Let (X1, Y 1),...,(Xn, Y n) be independent replicates of a random vector (X, Y ) IR IR { } ∈ × where p > 1,s > 2, and n>p+ s.
    [Show full text]
  • 5. the Student T Distribution
    Virtual Laboratories > 4. Special Distributions > 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5. The Student t Distribution In this section we will study a distribution that has special importance in statistics. In particular, this distribution will arise in the study of a standardized version of the sample mean when the underlying distribution is normal. The Probability Density Function Suppose that Z has the standard normal distribution, V has the chi-squared distribution with n degrees of freedom, and that Z and V are independent. Let Z T= √V/n In the following exercise, you will show that T has probability density function given by −(n +1) /2 Γ((n + 1) / 2) t2 f(t)= 1 + , t∈ℝ ( n ) √n π Γ(n / 2) 1. Show that T has the given probability density function by using the following steps. n a. Show first that the conditional distribution of T given V=v is normal with mean 0 a nd variance v . b. Use (a) to find the joint probability density function of (T,V). c. Integrate the joint probability density function in (b) with respect to v to find the probability density function of T. The distribution of T is known as the Student t distribution with n degree of freedom. The distribution is well defined for any n > 0, but in practice, only positive integer values of n are of interest. This distribution was first studied by William Gosset, who published under the pseudonym Student. In addition to supplying the proof, Exercise 1 provides a good way of thinking of the t distribution: the t distribution arises when the variance of a mean 0 normal distribution is randomized in a certain way.
    [Show full text]
  • 1 One Parameter Exponential Families
    1 One parameter exponential families The world of exponential families bridges the gap between the Gaussian family and general dis- tributions. Many properties of Gaussians carry through to exponential families in a fairly precise sense. • In the Gaussian world, there exact small sample distributional results (i.e. t, F , χ2). • In the exponential family world, there are approximate distributional results (i.e. deviance tests). • In the general setting, we can only appeal to asymptotics. A one-parameter exponential family, F is a one-parameter family of distributions of the form Pη(dx) = exp (η · t(x) − Λ(η)) P0(dx) for some probability measure P0. The parameter η is called the natural or canonical parameter and the function Λ is called the cumulant generating function, and is simply the normalization needed to make dPη fη(x) = (x) = exp (η · t(x) − Λ(η)) dP0 a proper probability density. The random variable t(X) is the sufficient statistic of the exponential family. Note that P0 does not have to be a distribution on R, but these are of course the simplest examples. 1.0.1 A first example: Gaussian with linear sufficient statistic Consider the standard normal distribution Z e−z2=2 P0(A) = p dz A 2π and let t(x) = x. Then, the exponential family is eη·x−x2=2 Pη(dx) / p 2π and we see that Λ(η) = η2=2: eta= np.linspace(-2,2,101) CGF= eta**2/2. plt.plot(eta, CGF) A= plt.gca() A.set_xlabel(r'$\eta$', size=20) A.set_ylabel(r'$\Lambda(\eta)$', size=20) f= plt.gcf() 1 Thus, the exponential family in this setting is the collection F = fN(η; 1) : η 2 Rg : d 1.0.2 Normal with quadratic sufficient statistic on R d As a second example, take P0 = N(0;Id×d), i.e.
    [Show full text]
  • Chapter 8 Fundamental Sampling Distributions And
    CHAPTER 8 FUNDAMENTAL SAMPLING DISTRIBUTIONS AND DATA DESCRIPTIONS 8.1 Random Sampling pling procedure, it is desirable to choose a random sample in the sense that the observations are made The basic idea of the statistical inference is that we independently and at random. are allowed to draw inferences or conclusions about a Random Sample population based on the statistics computed from the sample data so that we could infer something about Let X1;X2;:::;Xn be n independent random variables, the parameters and obtain more information about the each having the same probability distribution f (x). population. Thus we must make sure that the samples Define X1;X2;:::;Xn to be a random sample of size must be good representatives of the population and n from the population f (x) and write its joint proba- pay attention on the sampling bias and variability to bility distribution as ensure the validity of statistical inference. f (x1;x2;:::;xn) = f (x1) f (x2) f (xn): ··· 8.2 Some Important Statistics It is important to measure the center and the variabil- ity of the population. For the purpose of the inference, we study the following measures regarding to the cen- ter and the variability. 8.2.1 Location Measures of a Sample The most commonly used statistics for measuring the center of a set of data, arranged in order of mag- nitude, are the sample mean, sample median, and sample mode. Let X1;X2;:::;Xn represent n random variables. Sample Mean To calculate the average, or mean, add all values, then Bias divide by the number of individuals.
    [Show full text]
  • Chapter 4: Central Tendency and Dispersion
    Central Tendency and Dispersion 4 In this chapter, you can learn • how the values of the cases on a single variable can be summarized using measures of central tendency and measures of dispersion; • how the central tendency can be described using statistics such as the mode, median, and mean; • how the dispersion of scores on a variable can be described using statistics such as a percent distribution, minimum, maximum, range, and standard deviation along with a few others; and • how a variable’s level of measurement determines what measures of central tendency and dispersion to use. Schooling, Politics, and Life After Death Once again, we will use some questions about 1980 GSS young adults as opportunities to explain and demonstrate the statistics introduced in the chapter: • Among the 1980 GSS young adults, are there both believers and nonbelievers in a life after death? Which is the more common view? • On a seven-attribute political party allegiance variable anchored at one end by “strong Democrat” and at the other by “strong Republican,” what was the most Democratic attribute used by any of the 1980 GSS young adults? The most Republican attribute? If we put all 1980 95 96 PART II :: DESCRIPTIVE STATISTICS GSS young adults in order from the strongest Democrat to the strongest Republican, what is the political party affiliation of the person in the middle? • What was the average number of years of schooling completed at the time of the survey by 1980 GSS young adults? Were most of these twentysomethings pretty close to the average on
    [Show full text]
  • The Probability Lifesaver: Order Statistics and the Median Theorem
    The Probability Lifesaver: Order Statistics and the Median Theorem Steven J. Miller December 30, 2015 Contents 1 Order Statistics and the Median Theorem 3 1.1 Definition of the Median 5 1.2 Order Statistics 10 1.3 Examples of Order Statistics 15 1.4 TheSampleDistributionoftheMedian 17 1.5 TechnicalboundsforproofofMedianTheorem 20 1.6 TheMedianofNormalRandomVariables 22 2 • Greetings again! In this supplemental chapter we develop the theory of order statistics in order to prove The Median Theorem. This is a beautiful result in its own, but also extremely important as a substitute for the Central Limit Theorem, and allows us to say non- trivial things when the CLT is unavailable. Chapter 1 Order Statistics and the Median Theorem The Central Limit Theorem is one of the gems of probability. It’s easy to use and its hypotheses are satisfied in a wealth of problems. Many courses build towards a proof of this beautiful and powerful result, as it truly is ‘central’ to the entire subject. Not to detract from the majesty of this wonderful result, however, what happens in those instances where it’s unavailable? For example, one of the key assumptions that must be met is that our random variables need to have finite higher moments, or at the very least a finite variance. What if we were to consider sums of Cauchy random variables? Is there anything we can say? This is not just a question of theoretical interest, of mathematicians generalizing for the sake of generalization. The following example from economics highlights why this chapter is more than just of theoretical interest.
    [Show full text]
  • Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F
    Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F Course : Basic Econometrics : HC43 / Statistics B.A. Hons Economics, Semester IV/ Semester III Delhi University Course Instructor: Siddharth Rathore Assistant Professor Economics Department, Gargi College Siddharth Rathore guj75845_appC.qxd 4/16/09 12:41 PM Page 461 APPENDIX C SOME IMPORTANT PROBABILITY DISTRIBUTIONS In Appendix B we noted that a random variable (r.v.) can be described by a few characteristics, or moments, of its probability function (PDF or PMF), such as the expected value and variance. This, however, presumes that we know the PDF of that r.v., which is a tall order since there are all kinds of random variables. In practice, however, some random variables occur so frequently that statisticians have determined their PDFs and documented their properties. For our purpose, we will consider only those PDFs that are of direct interest to us. But keep in mind that there are several other PDFs that statisticians have studied which can be found in any standard statistics textbook. In this appendix we will discuss the following four probability distributions: 1. The normal distribution 2. The t distribution 3. The chi-square (␹2 ) distribution 4. The F distribution These probability distributions are important in their own right, but for our purposes they are especially important because they help us to find out the probability distributions of estimators (or statistics), such as the sample mean and sample variance. Recall that estimators are random variables. Equipped with that knowledge, we will be able to draw inferences about their true population values.
    [Show full text]
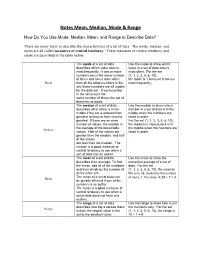
  • Notes Mean, Median, Mode & Range
    Notes Mean, Median, Mode & Range How Do You Use Mode, Median, Mean, and Range to Describe Data? There are many ways to describe the characteristics of a set of data. The mode, median, and mean are all called measures of central tendency. These measures of central tendency and range are described in the table below. The mode of a set of data Use the mode to show which describes which value occurs value in a set of data occurs most frequently. If two or more most often. For the set numbers occur the same number {1, 1, 2, 3, 5, 6, 10}, of times and occur more often the mode is 1 because it occurs Mode than all the other numbers in the most frequently. set, those numbers are all modes for the data set. If each number in the set occurs the same number of times, the set of data has no mode. The median of a set of data Use the median to show which describes what value is in the number in a set of data is in the middle if the set is ordered from middle when the numbers are greatest to least or from least to listed in order. greatest. If there are an even For the set {1, 1, 2, 3, 5, 6, 10}, number of values, the median is the median is 3 because it is in the average of the two middle the middle when the numbers are Median values. Half of the values are listed in order. greater than the median, and half of the values are less than the median.
    [Show full text]
  • Global Investigation of Return Autocorrelation and Its Determinants
    Global investigation of return autocorrelation and its determinants Pawan Jaina,, Wenjun Xueb aUniversity of Wyoming bFlorida International University ABSTRACT We estimate global return autocorrelation by using the quantile autocorrelation model and investigate its determinants across 43 stock markets from 1980 to 2013. Although our results document a decline in autocorrelation across the entire sample period for all countries, return autocorrelation is significantly larger in emerging markets than in developed markets. The results further document that larger and liquid stock markets have lower return autocorrelation. We also find that price limits in most emerging markets result in higher return autocorrelation. We show that the disclosure requirement, public enforcement, investor psychology, and market characteristics significantly affect return autocorrelation. Our results document that investors from different cultural backgrounds and regulation regimes react differently to corporate disclosers, which affects return autocorrelation. Keywords: Return autocorrelation, Global stock markets, Quantile autoregression model, Legal environment, Investor psychology, Hofstede’s cultural dimensions JEL classification: G12, G14, G15 Corresponding author, E-mail: [email protected]; fax: 307-766-5090. 1. Introduction One of the most striking asset pricing anomalies is the existence of large, positive, short- horizon return autocorrelation in stock portfolios, first documented in Conrad and Kaul (1988) and Lo and MacKinlay (1990). This existence of
    [Show full text]
  • Volatility Modeling Using the Student's T Distribution
    Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Economics Aris Spanos, Chair Richard Ashley Raman Kumar Anya McGuirk Dennis Yang August 29, 2003 Blacksburg, Virginia Keywords: Student’s t Distribution, Multivariate GARCH, VAR, Exchange Rates Copyright 2003, Maria S. Heracleous Volatility Modeling Using the Student’s t Distribution Maria S. Heracleous (ABSTRACT) Over the last twenty years or so the Dynamic Volatility literature has produced a wealth of uni- variateandmultivariateGARCHtypemodels.Whiletheunivariatemodelshavebeenrelatively successful in empirical studies, they suffer from a number of weaknesses, such as unverifiable param- eter restrictions, existence of moment conditions and the retention of Normality. These problems are naturally more acute in the multivariate GARCH type models, which in addition have the problem of overparameterization. This dissertation uses the Student’s t distribution and follows the Probabilistic Reduction (PR) methodology to modify and extend the univariate and multivariate volatility models viewed as alternative to the GARCH models. Its most important advantage is that it gives rise to internally consistent statistical models that do not require ad hoc parameter restrictions unlike the GARCH formulations. Chapters 1 and 2 provide an overview of my dissertation and recent developments in the volatil- ity literature. In Chapter 3 we provide an empirical illustration of the PR approach for modeling univariate volatility. Estimation results suggest that the Student’s t AR model is a parsimonious and statistically adequate representation of exchange rate returns and Dow Jones returns data.
    [Show full text]
  • The Value at the Mode in Multivariate T Distributions: a Curiosity Or Not?
    The value at the mode in multivariate t distributions: a curiosity or not? Christophe Ley and Anouk Neven Universit´eLibre de Bruxelles, ECARES and D´epartement de Math´ematique,Campus Plaine, boulevard du Triomphe, CP210, B-1050, Brussels, Belgium Universit´edu Luxembourg, UR en math´ematiques,Campus Kirchberg, 6, rue Richard Coudenhove-Kalergi, L-1359, Luxembourg, Grand-Duchy of Luxembourg e-mail: [email protected]; [email protected] Abstract: It is a well-known fact that multivariate Student t distributions converge to multivariate Gaussian distributions as the number of degrees of freedom ν tends to infinity, irrespective of the dimension k ≥ 1. In particular, the Student's value at the mode (that is, the normalizing ν+k Γ( 2 ) constant obtained by evaluating the density at the center) cν;k = k=2 ν converges towards (πν) Γ( 2 ) the Gaussian value at the mode c = 1 . In this note, we prove a curious fact: c tends k (2π)k=2 ν;k monotonically to ck for each k, but the monotonicity changes from increasing in dimension k = 1 to decreasing in dimensions k ≥ 3 whilst being constant in dimension k = 2. A brief discussion raises the question whether this a priori curious finding is a curiosity, in fine. AMS 2000 subject classifications: Primary 62E10; secondary 60E05. Keywords and phrases: Gamma function, Gaussian distribution, value at the mode, Student t distribution, tail weight. 1. Foreword. One of the first things we learn about Student t distributions is the fact that, when the degrees of freedom ν tend to infinity, we retrieve the Gaussian distribution, which has the lightest tails in the Student family of distributions.
    [Show full text]