Building an ALU (Part 1)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12]. -

Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R. -

Implementation of Carry Tree Adders and Compare with RCA and CSLA
International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit. -
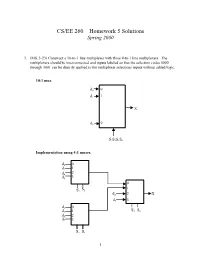
CS/EE 260 – Homework 5 Solutions Spring 2000
CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder. -

UNIT 8B a Full Adder
UNIT 8B Computer Organization: Levels of Abstraction 15110 Principles of Computing, 1 Carnegie Mellon University - CORTINA A Full Adder C ABCin Cout S in 0 0 0 A 0 0 1 0 1 0 B 0 1 1 1 0 0 1 0 1 C S out 1 1 0 1 1 1 15110 Principles of Computing, 2 Carnegie Mellon University - CORTINA 1 A Full Adder C ABCin Cout S in 0 0 0 0 0 A 0 0 1 0 1 0 1 0 0 1 B 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 C S out 1 1 0 1 0 1 1 1 1 1 ⊕ ⊕ S = A B Cin ⊕ ∧ ∨ ∧ Cout = ((A B) C) (A B) 15110 Principles of Computing, 3 Carnegie Mellon University - CORTINA Full Adder (FA) AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 4 Carnegie Mellon University - CORTINA 2 Another Full Adder (FA) http://students.cs.tamu.edu/wanglei/csce350/handout/lab6.html AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 5 Carnegie Mellon University - CORTINA 8-bit Full Adder A7 B7 A2 B2 A1 B1 A0 B0 1-bit 1-bit 1-bit 1-bit ... Cout Full Full Full Full Cin Adder Adder Adder Adder S7 S2 S1 S0 AB 8 ⁄ ⁄ 8 C 8-bit C out FA in ⁄ 8 S 15110 Principles of Computing, 6 Carnegie Mellon University - CORTINA 3 Multiplexer (MUX) • A multiplexer chooses between a set of inputs. D1 D 2 MUX F D3 D ABF 4 0 0 D1 AB 0 1 D2 1 0 D3 1 1 D4 http://www.cise.ufl.edu/~mssz/CompOrg/CDAintro.html 15110 Principles of Computing, 7 Carnegie Mellon University - CORTINA Arithmetic Logic Unit (ALU) OP 1OP 0 Carry In & OP OP 0 OP 1 F 0 0 A ∧ B 0 1 A ∨ B 1 0 A 1 1 A + B http://cs-alb-pc3.massey.ac.nz/notes/59304/l4.html 15110 Principles of Computing, 8 Carnegie Mellon University - CORTINA 4 Flip Flop • A flip flop is a sequential circuit that is able to maintain (save) a state. -

Soft Machines Targets Ipcbottleneck
SOFT MACHINES TARGETS IPC BOTTLENECK New CPU Approach Boosts Performance Using Virtual Cores By Linley Gwennap (October 27, 2014) ................................................................................................................... Coming out of stealth mode at last week’s Linley Pro- president/CTO Mohammad Abdallah. Investors include cessor Conference, Soft Machines disclosed a new CPU AMD, GlobalFoundries, and Samsung as well as govern- technology that greatly improves performance on single- ment investment funds from Abu Dhabi (Mubdala), Russia threaded applications. The new VISC technology can con- (Rusnano and RVC), and Saudi Arabia (KACST and vert a single software thread into multiple virtual threads, Taqnia). Its board of directors is chaired by Global Foun- which it can then divide across multiple physical cores. dries CEO Sanjay Jha and includes legendary entrepreneur This conversion happens inside the processor hardware Gordon Campbell. and is thus invisible to the application and the software Soft Machines hopes to license the VISC technology developer. Although this capability may seem impossible, to other CPU-design companies, which could add it to Soft Machines has demonstrated its performance advan- their existing CPU cores. Because its fundamental benefit tage using a test chip that implements a VISC design. is better IPC, VISC could aid a range of applications from Without VISC, the only practical way to improve single-thread performance is to increase the parallelism Application (sequential code) (instructions per cycle, or IPC) of the CPU microarchi- Single Thread tecture. Taken to the extreme, this approach results in massive designs such as Intel’s Haswell and IBM’s Power8 OS and Hypervisor that deliver industry-leading performance but waste power Standard ISA and die area. -

Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R
et International Journal on Emerging Technologies 11 (2): 668-673(2020) ISSN No. (Print): 0975-8364 ISSN No. (Online): 2249-3255 Arithmetic and Logical Unit Design for Area Optimization for Microcontroller Amrut Anilrao Purohit 1,2 , Mohammed Riyaz Ahmed 2 and R. Venkata Siva Reddy 2 1Research Scholar, VTU Belagavi (Karnataka), India. 2School of Electronics and Communication Engineering, REVA University Bengaluru, (Karnataka), India. (Corresponding author: Amrut Anilrao Purohit) (Received 04 January 2020, Revised 02 March 2020, Accepted 03 March 2020) (Published by Research Trend, Website: www.researchtrend.net) ABSTRACT: Arithmetic and Logic Unit (ALU) can be understood with basic knowledge of digital electronics and any engineer will go through the details only once. The advantage of knowing ALU in detail is two- folded: firstly, programming of the processing device can be efficient and secondly, can design a new ALU architecture as per the various constraints of the use cases. The miniaturization of digital circuits can be achieved by either reducing the size of transistor (Moore’s law) or by optimizing the gate count of the circuit. The first has been explored extensively while the latter has been ignored which deals with the application of Boolean rules and requires sound knowledge of logic design. The ultimate outcome is to have an area optimized architecture/approach that optimizes the circuit at gate level. The design of ALU is for various processing devices varies with the device/system requirements. The area optimization places a significant role in the chip design. Here in this work, we have attempted to design an ALU which is area efficient while being loaded with additional functionality necessary for microcontrollers. -

Design of High Speed and Low Power Six Transistor Full Adder Using Two Transistor Xor Gate
International Journal of Electronics, Communication & Instrumentation Engineering Research and Development (IJECIERD) ISSN 2249-684X Vol. 3, Issue 1, Mar 2013, 87-96 © TJPRC Pvt. Ltd. DESIGN OF HIGH SPEED AND LOW POWER SIX TRANSISTOR FULL ADDER USING TWO TRANSISTOR XOR GATE B. DILLI KUMAR, K. CHARAN KUMAR & T. NAVEEN KUMAR M. Tech (VLSI), Department of ECE, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India ABSTRACT Full adder is one of the major components in the design of many sophisticated hardware circuits. In this paper the full adder has been designed by using a new efficient design with less number of transistors. A 2 transistor XOR gate has been proposed with the help of two PMOS (Positive Metal Oxide Semiconductor) transistors. By using this 2T XOR gate the size of the full adder has been decreased to a large extent which can be implemented with only 6 transistors. The proposed full adder has a significant improvement in silicon area and power delay product when compared to the previous 8T full adder circuits. Further the proposed adder requires less area to perform a required logic function. Further, the proposed full adder has less power dissipation which makes it suitable for many of the low power applications and because of less area requirement the proposed design can be used in many of the portable applications also . KEYWORDS: Full Adder, XOR, Less Area, Speed, Low Power, Delay, Less Transistor Count, Low Power VLSI INTRODUCTION Full adder is one of the basic building blocks of many of the digital VLSI circuits. Several refinements has been made regarding its structure since its invention. -

Unit 8 : Microprocessor Architecture
Unit 8 : Microprocessor Architecture Lesson 1 : Microcomputer Structure 1.1. Learning Objectives On completion of this lesson you will be able to : ♦ draw the block diagram of a simple computer ♦ understand the function of different units of a microcomputer ♦ learn the basic operation of microcomputer bus system. 1.2. Digital Computer A digital computer is a multipurpose, programmable machine that reads A digital computer is a binary instructions from its memory, accepts binary data as input and multipurpose, programmable processes data according to those instructions, and provides results as machine. output. 1.3. Basic Computer System Organization Every computer contains five essential parts or units. They are Basic computer system organization. i. the arithmetic logic unit (ALU) ii. the control unit iii. the memory unit iv. the input unit v. the output unit. 1.3.1. The Arithmetic and Logic Unit (ALU) The arithmetic and logic unit (ALU) is that part of the computer that The arithmetic and logic actually performs arithmetic and logical operations on data. All other unit (ALU) is that part of elements of the computer system - control unit, register, memory, I/O - the computer that actually are there mainly to bring data into the ALU to process and then to take performs arithmetic and the results back out. logical operations on data. An arithmetic and logic unit and, indeed, all electronic components in the computer are based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations. Data are presented to the ALU in registers. These registers are temporary storage locations within the CPU that are connected by signal paths of the ALU. -

Computer Architecture Out-Of-Order Execution
Computer Architecture Out-of-order Execution By Yoav Etsion With acknowledgement to Dan Tsafrir, Avi Mendelson, Lihu Rappoport, and Adi Yoaz 1 Computer Architecture 2013– Out-of-Order Execution The need for speed: Superscalar • Remember our goal: minimize CPU Time CPU Time = duration of clock cycle × CPI × IC • So far we have learned that in order to Minimize clock cycle ⇒ add more pipe stages Minimize CPI ⇒ utilize pipeline Minimize IC ⇒ change/improve the architecture • Why not make the pipeline deeper and deeper? Beyond some point, adding more pipe stages doesn’t help, because Control/data hazards increase, and become costlier • (Recall that in a pipelined CPU, CPI=1 only w/o hazards) • So what can we do next? Reduce the CPI by utilizing ILP (instruction level parallelism) We will need to duplicate HW for this purpose… 2 Computer Architecture 2013– Out-of-Order Execution A simple superscalar CPU • Duplicates the pipeline to accommodate ILP (IPC > 1) ILP=instruction-level parallelism • Note that duplicating HW in just one pipe stage doesn’t help e.g., when having 2 ALUs, the bottleneck moves to other stages IF ID EXE MEM WB • Conclusion: Getting IPC > 1 requires to fetch/decode/exe/retire >1 instruction per clock: IF ID EXE MEM WB 3 Computer Architecture 2013– Out-of-Order Execution Example: Pentium Processor • Pentium fetches & decodes 2 instructions per cycle • Before register file read, decide on pairing Can the two instructions be executed in parallel? (yes/no) u-pipe IF ID v-pipe • Pairing decision is based… On data -

Performance of a Computer (Chapter 4) Vishwani D
ELEC 5200-001/6200-001 Computer Architecture and Design Fall 2013 Performance of a Computer (Chapter 4) Vishwani D. Agrawal & Victor P. Nelson epartment of Electrical and Computer Engineering Auburn University, Auburn, AL 36849 ELEC 5200-001/6200-001 Performance Fall 2013 . Lecture 1 What is Performance? Response time: the time between the start and completion of a task. Throughput: the total amount of work done in a given time. Some performance measures: MIPS (million instructions per second). MFLOPS (million floating point operations per second), also GFLOPS, TFLOPS (1012), etc. SPEC (System Performance Evaluation Corporation) benchmarks. LINPACK benchmarks, floating point computing, used for supercomputers. Synthetic benchmarks. ELEC 5200-001/6200-001 Performance Fall 2013 . Lecture 2 Small and Large Numbers Small Large 10-3 milli m 103 kilo k 10-6 micro μ 106 mega M 10-9 nano n 109 giga G 10-12 pico p 1012 tera T 10-15 femto f 1015 peta P 10-18 atto 1018 exa 10-21 zepto 1021 zetta 10-24 yocto 1024 yotta ELEC 5200-001/6200-001 Performance Fall 2013 . Lecture 3 Computer Memory Size Number bits bytes 210 1,024 K Kb KB 220 1,048,576 M Mb MB 230 1,073,741,824 G Gb GB 240 1,099,511,627,776 T Tb TB ELEC 5200-001/6200-001 Performance Fall 2013 . Lecture 4 Units for Measuring Performance Time in seconds (s), microseconds (μs), nanoseconds (ns), or picoseconds (ps). Clock cycle Period of the hardware clock Example: one clock cycle means 1 nanosecond for a 1GHz clock frequency (or 1GHz clock rate) CPU time = (CPU clock cycles)/(clock rate) Cycles per instruction (CPI): average number of clock cycles used to execute a computer instruction. -

Chap01: Computer Abstractions and Technology
CHAPTER 1 Computer Abstractions and Technology 1.1 Introduction 3 1.2 Eight Great Ideas in Computer Architecture 11 1.3 Below Your Program 13 1.4 Under the Covers 16 1.5 Technologies for Building Processors and Memory 24 1.6 Performance 28 1.7 The Power Wall 40 1.8 The Sea Change: The Switch from Uniprocessors to Multiprocessors 43 1.9 Real Stuff: Benchmarking the Intel Core i7 46 1.10 Fallacies and Pitfalls 49 1.11 Concluding Remarks 52 1.12 Historical Perspective and Further Reading 54 1.13 Exercises 54 CMPS290 Class Notes (Chap01) Page 1 / 24 by Kuo-pao Yang 1.1 Introduction 3 Modern computer technology requires professionals of every computing specialty to understand both hardware and software. Classes of Computing Applications and Their Characteristics Personal computers o A computer designed for use by an individual, usually incorporating a graphics display, a keyboard, and a mouse. o Personal computers emphasize delivery of good performance to single users at low cost and usually execute third-party software. o This class of computing drove the evolution of many computing technologies, which is only about 35 years old! Server computers o A computer used for running larger programs for multiple users, often simultaneously, and typically accessed only via a network. o Servers are built from the same basic technology as desktop computers, but provide for greater computing, storage, and input/output capacity. Supercomputers o A class of computers with the highest performance and cost o Supercomputers consist of tens of thousands of processors and many terabytes of memory, and cost tens to hundreds of millions of dollars.