Stock Market Synchronicity and the Global Trade Network: a Random-Walk Approach
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
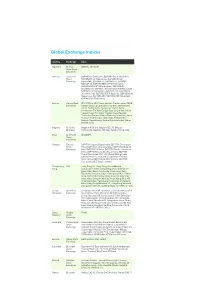
Global Exchange Indices
Global Exchange Indices Country Exchange Index Argentina Buenos MERVAL, BURCAP Aires Stock Exchange Australia Australian S&P/ASX All Ordinaries, S&P/ASX Small Ordinaries, Stock S&P/ASX Small Resources, S&P/ASX Small Exchange Industriials, S&P/ASX 20, S&P/ASX 50, S&P/ASX MIDCAP 50, S&P/ASX MIDCAP 50 Resources, S&P/ASX MIDCAP 50 Industrials, S&P/ASX All Australian 50, S&P/ASX 100, S&P/ASX 100 Resources, S&P/ASX 100 Industrials, S&P/ASX 200, S&P/ASX All Australian 200, S&P/ASX 200 Industrials, S&P/ASX 200 Resources, S&P/ASX 300, S&P/ASX 300 Industrials, S&P/ASX 300 Resources Austria Vienna Stock ATX, ATX Five, ATX Prime, Austrian Traded Index, CECE Exchange Overall Index, CECExt Index, Chinese Traded Index, Czech Traded Index, Hungarian Traded Index, Immobilien ATX, New Europe Blue Chip Index, Polish Traded Index, Romanian Traded Index, Russian Depository Extended Index, Russian Depository Index, Russian Traded Index, SE Europe Traded Index, Serbian Traded Index, Vienna Dynamic Index, Weiner Boerse Index Belgium Euronext Belgium All Share, Belgium BEL20, Belgium Brussels Continuous, Belgium Mid Cap, Belgium Small Cap Brazil Sao Paulo IBOVESPA Stock Exchange Canada Toronto S&P/TSX Capped Equity Index, S&P/TSX Completion Stock Index, S&P/TSX Composite Index, S&P/TSX Equity 60 Exchange Index S&P/TSX 60 Index, S&P/TSX Equity Completion Index, S&P/TSX Equity SmallCap Index, S&P/TSX Global Gold Index, S&P/TSX Global Mining Index, S&P/TSX Income Trust Index, S&P/TSX Preferred Share Index, S&P/TSX SmallCap Index, S&P/TSX Composite GICS Sector Indexes -

Weak-Form Market Efficiency, Estimation Interval and the Nigerian Stock Exchange: Empirical Evidence
WEAK-FORM MARKET EFFICIENCY, ESTIMATION INTERVAL AND THE NIGERIAN STOCK EXCHANGE: EMPIRICAL EVIDENCE Onyemachi Maxwell Ogbulu, Abia State University Abstract Given the desirability of efficient capital markets in aiding optimal resource mobilization and allocation in the financial system, this paper is an attempt to investigate the efficiency level of the Nigerian Stock Exchange (NSE) across different data estimation intervals with reference to the weak-form variant of the Efficient Market Hypothesis (EMH). The paper employed daily, weekly, monthly and quarterly aggregate stock price data using the NSE All Share Index series from 4th January, 1999 to 31st December, 2013 to test for the weak-form efficiency of the NSE using a combination of seven (7) statistical and parametric tools namely- Autocorrelation tests, the ADF and P-P unit root tests, Variance Ratio tests, the Normality/Random Walk tests, the Granger Causality test, the ARCH-GARCH test and Regression rest. The empirical results of the investigation indicate that on balance the NSE is weak-form inefficient when daily, weekly, monthly and quarterly prices are examined irrespective of the estimation interval and the parametric test employed in the tests. It is to be noted from the findings that the NSE is still weak-form inefficient despite the implementation of various capital market reforms undertaken in the recent past as well as the adoption of automation and ICT in the operations of the Exchange. It is therefore recommended that these salutary reforms and policies should be intensified and sustained to ensure efficiency of the NSE. Keywords: Weak-form efficiency, Efficient Market Hypothesis, Estimation Interval, Parametric Tests. -

Financial Market Data for R/Rmetrics
Financial Market Data for R/Rmetrics Diethelm Würtz Andrew Ellis Yohan Chalabi Rmetrics Association & Finance Online R/Rmetrics eBook Series R/Rmetrics eBooks is a series of electronic books and user guides aimed at students and practitioner who use R/Rmetrics to analyze financial markets. A Discussion of Time Series Objects for R in Finance (2009) Diethelm Würtz, Yohan Chalabi, Andrew Ellis R/Rmetrics Meielisalp 2009 Proceedings of the Meielisalp Workshop 2011 Editor Diethelm Würtz Basic R for Finance (2010), Diethelm Würtz, Yohan Chalabi, Longhow Lam, Andrew Ellis Chronological Objects with Rmetrics (2010), Diethelm Würtz, Yohan Chalabi, Andrew Ellis Portfolio Optimization with R/Rmetrics (2010), Diethelm Würtz, William Chen, Yohan Chalabi, Andrew Ellis Financial Market Data for R/Rmetrics (2010) Diethelm W?rtz, Andrew Ellis, Yohan Chalabi Indian Financial Market Data for R/Rmetrics (2010) Diethelm Würtz, Mahendra Mehta, Andrew Ellis, Yohan Chalabi Asian Option Pricing with R/Rmetrics (2010) Diethelm Würtz R/Rmetrics Singapore 2010 Proceedings of the Singapore Workshop 2010 Editors Diethelm Würtz, Mahendra Mehta, David Scott, Juri Hinz R/Rmetrics Meielisalp 2011 Proceedings of the Meielisalp Summer School and Workshop 2011 Editor Diethelm Würtz III tinn-R Editor (2010) José Cláudio Faria, Philippe Grosjean, Enio Galinkin Jelihovschi and Ri- cardo Pietrobon R/Rmetrics Meielisalp 2011 Proceedings of the Meielisalp Summer Scholl and Workshop 2011 Editor Diethelm Würtz R/Rmetrics Meielisalp 2012 Proceedings of the Meielisalp Summer Scholl and Workshop 2012 Editor Diethelm Würtz Topics in Empirical Finance with R and Rmetrics (2013), Patrick Hénaff FINANCIAL MARKET DATA FOR R/RMETRICS DIETHELM WÜRTZ ANDREW ELLIS YOHAN CHALABI RMETRICS ASSOCIATION &FINANCE ONLINE Series Editors: Prof. -

On Determination of Market Price of One Ordinary Registered Share of the Moscow Exchange (State Registration Number 1-05-8443-H Dated 16.11.2011)
2, 3-ya ulitsa Yamskogo Polya, bld. 7, office 301, Moscow, 125040 Tel.: +7 (495) 717-01-01 +7 (495) 557-07-97 www.evcons.ru REPORT No. 134/16 dated June 29, 2016 On determination of market price of one ordinary registered share of the Moscow Exchange (state registration number 1-05-8443-H dated 16.11.2011) Customer: Moscow Exchange Contractor: Everest Consulting Moscow 2016 EVEREST Consulting LLC 1 Att: Evgeny Fetisov CFO Moscow Exchange Dear Evgeny, Under Agreement No.134/16 dated 16.06.2016 executed by and between Everest Consulting Limited Liability Company (hereinafter Everest Consulting LLC, the Contractor), and Public Joint-Stock Company Moscow Exchange MICEX-RTS (hereinafter the Moscow Exchange, the Customer), the appraiser employed by the Contractor (hereinafter the Appraiser) carried out valuation of one registered ordinary share of the Moscow Exchange (hereinafter the Object of Valuation). The principle task and intended use of valuation was to measure the market price of the Object of Valuation for the purpose of share buyback from shareholders who voted against the corporate restructuring or failed to participate in voting in pursuance with clause 1 and clause 3 Article 75 of the Federal Law No.208-FZ On Joint-stock Companies dated 26 December 1995. The valuation was done in accordance with the Federal Law No.135-FZ On Valuation Activity in the Russian Federation dated 29 July 1998, Federal Evaluation Standard General Concepts of the Valuation, Approaches and Requirements to Carrying Out the Valuation (FES No.1) approved by the Order of the Ministry of Economy No. -

Msci Index Calculation Methodology
INDEX METHODOLOGY MSCI INDEX CALCULATION METHODOLOGY Index Calculation Methodology for the MSCI Equity Indexes Esquivel, Carlos July 2018 JULY 2018 MSCI INDEX CALCULATION METHODOLOGY | JULY 2018 CONTENTS Introduction ....................................................................................... 4 MSCI Equity Indexes........................................................................... 5 1 MSCI Price Index Methodology ................................................... 6 1.1 Price Index Level ....................................................................................... 6 1.2 Price Index Level (Alternative Calculation Formula – Contribution Method) ............................................................................................................ 10 1.3 Next Day Initial Security Weight ............................................................ 15 1.4 Closing Index Market Capitalization Today USD (Unadjusted Market Cap Today USD) ........................................................................................................ 16 1.5 Security Index Of Price In Local .............................................................. 17 1.6 Note on Index Calculation In Local Currency ......................................... 19 1.7 Conversion of Indexes Into Another Currency ....................................... 19 2 MSCI Daily Total Return (DTR) Index Methodology ................... 21 2.1 Calculation Methodology ....................................................................... 21 2.2 Reinvestment -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

INDEX RULE BOOK Leverage, Short, and Bear Indices
INDEX RULE BOOK Leverage, Short, and Bear Indices Version 20-02 Effective from 15 May 2020 indices.euronext.com Index 1. Index Summary 1 2. Governance and Disclaimer 8 2.1 Indices 8 2.2 Administrator 8 2.3 Cases not covered in rules 8 2.4 Rule book changes 8 2.5 Liability 8 2.6 Ownership and trademarks 8 3. Calculation 9 3.1 Definition and Composition of the Index 9 3.2 Calculation of the Leverage Indices 9 3.3 Calculation of the Bear and Short Indices 9 3.4 Reverse split of index level 10 3.5 Split of index level 10 3.6 Financing Adjustment Rate (FIN) 10 4. Publication 11 4.1 Dissemination of Index Values 11 4.2 Exceptional Market Conditions and Corrections 11 4.3 Announcement Policy 14 5. ESG Disclosures 15 1. INDEX SUMMARY Factsheet Leverage, Short and Bear indices Index names Various based on AEX®, BEL 20®, CAC 40®, PSI 20® and ISEQ® Index type Indices are based on price index versions or Net return index or Gross return index versions. Administrator Euronext Paris is the Administrator and is responsible for the day-to-day management of the index. The underlying indices have independent Steering Committees acting as Independent Supervisor. Calculation Based on daily leverage. May include spread on interest rate or Financing Adjustment rate in the calculation Rule for exceptional trading Either suspend or reset if underlying index moved beyond certain threshold. See reference circumstances table. 1 Mnemo Full name Underlying Factor Rule for ISIN Base level index exceptional and date trading circumstances AEX® based AEXLV AEX® Leverage AEX® 2 Suspend if Underlying QS0011095898 1,000 at Index < 75% of close 31Dec2002 of previous day AEXNL AEX® Leverage AEX® NR 2 Suspend if Underlying QS0011216205 1,000 at NR Index < 75% of close 31Dec2002 of previous day AEXTL AEX® Leverage AEX® GR 2 Suspend if Underlying QS0011179239 1,000 at GR Index < 75% of close 31Dec2002 of previous day AEX3L AEX® NR 3 Reset if Underlying QS0011230115 10,000 at AEX® X3 Leverage Index < 85% of close 31Dec2008 NR of previous day. -

Execution Version
Execution Version GUARANTEED SENIOR SECURED NOTES PROGRAMME issued by GOLDMAN SACHS INTERNATIONAL in respect of which the payment and delivery obligations are guaranteed by THE GOLDMAN SACHS GROUP, INC. (the “PROGRAMME”) PRICING SUPPLEMENT DATED 23rd SEPTEMBER 2020 SERIES 2020-12 SENIOR SECURED EXTENDIBLE FIXED RATE NOTES (the “SERIES”) ISIN: XS2233188510 Common Code: 223318851 This document constitutes the Pricing Supplement of the above Series of Secured Notes (the “Secured Notes”) and must be read in conjunction with the Base Listing Particulars dated 25 September 2019, as supplemented from time to time (the “Base Prospectus”), and in particular, the Base Terms and Conditions of the Secured Notes, as set out therein. Full information on the Issuer, The Goldman Sachs Group. Inc. (the “Guarantor”), and the terms and conditions of the Secured Notes, is only available on the basis of the combination of this Pricing Supplement and the Base Listing Particulars as so supplemented. The Base Listing Particulars has been published at www.ise.ie and is available for viewing during normal business hours at the registered office of the Issuer, and copies may be obtained from the specified office of the listing agent in Ireland. The Issuer accepts responsibility for the information contained in this Pricing Supplement. To the best of the knowledge and belief of the Issuer and the Guarantor the information contained in the Base Listing Particulars, as completed by this Pricing Supplement in relation to the Series of Secured Notes referred to above, is true and accurate in all material respects and, in the context of the issue of this Series, there are no other material facts the omission of which would make any statement in such information misleading. -

Ned Davis Research Group
Ned Davis Research Group THE OUTLooK FOR StoCKS, CoMMODITIES, AND GLOBAL THEMES: SECULAR AND CYCLICAL INFLUENCES Atlanta MTA & CFA Society of Atlanta | September 24, 2008 Tim Hayes, CMT, Chief Investment Strategist The NDR Approach • Identify investment themes and stay with them until a sentiment extreme is reached. • We say… » "Go with the flow until it reaches an extreme and then reverses." » "The big money is made on the big moves." » "Let your profits run, cut your losses short." • We develop reliable indicators and models based on… » "The Tape" – Trend, momentum, confirmation & divergence. » Investor psychology – Sentiment and valuation extremes. » Liquidity – Monetary and economic conditions, supply & demand. • In summary, NDR approach is… » Objective » Disciplined » Risk-Averse » Flexible 1 Ned Davis Research Group Please see important disclosures at the end of this document. CURRENT POSITIONS Global Allocation: Overweight/Bullish: Underweight/Bearish: Stocks » Bonds (by 10%) » Stocks (by 15%) Cash 40% » Cash (by 5%) 15% Bonds 45% » Pacific ex. Japan » U.K. » U.S. » Japan U.S. Allocation: Stocks 40% Cash 20% » Cash (by 10%) » Stocks (by 15%) » Bonds (by 5%) Bonds 40% Styles: » Growth » Value Sectors: » Energy » Consumer Discretionary » Basic Resources » Financials » Consumer Staples » Utilities Commodities: » Correction within secular uptrend Bonds: » 105% of benchmark duration Neutral Positions: » Large-caps vs. Small-caps » Yield curve 2 Ned Davis Research Group Please see important disclosures at the end of this document. We've -

Thomson One Symbols
THOMSON ONE SYMBOLS QUICK REFERENCE CARD QUOTES FOR LISTED SECURITIES TO GET A QUOTE FOR TYPE EXAMPLE Specific Exchange Hyphen followed by exchange qualifier after the symbol IBM-N (N=NYSE) Warrant ' after the symbol IBM' When Issued 'RA after the symbol IBM'RA Class 'letter representing class IBM'A Preferred .letter representing class IBM.B Currency Rates symbol=-FX GBP=-FX QUOTES FOR ETF TO GET A QUOTE FOR TYPE Net Asset Value .NV after the ticker Indicative Value .IV after the ticker Estimated Cash Amount Per Creation Unit .EU after the ticker Shares Outstanding Value .SO after the ticker Total Cash Amount Per Creation Unit .TC after the ticker To get Net Asset Value for CEF, type XsymbolX. QRG-383 Date of issue: 15 December 2015 © 2015 Thomson Reuters. All rights reserved. Thomson Reuters disclaims any and all liability arising from the use of this document and does not guarantee that any information contained herein is accurate or complete. This document contains information proprietary to Thomson Reuters and may not be reproduced, transmitted, or distributed in whole or part without the express written permission of Thomson Reuters. THOMSON ONE SYMBOLS Quick Reference Card MAJOR INDEXES US INDEXES THE AMERICAS INDEX SYMBOL Dow Jones Industrial Average .DJIA Airline Index XAL Dow Jones Composite .COMP AMEX Computer Tech. Index XCI MSCI ACWI 892400STRD-MS AMEX Institutional Index XII MSCI World 990100STRD-MS AMEX Internet Index IIX MSCI EAFE 990300STRD-MS AMEX Oil Index XOI MSCI Emerging Markets 891800STRD-MS AMEX Pharmaceutical Index -

Effects of Carbon Pricing on EU Equity Markets
Stockholm School of Economics Master Thesis in Finance Effects of Carbon Pricing on EU Equity Markets Andrii Shekhirev* 2011.06.20 The current work examines whether the price changes of European Union Allowance (EUA) contracts for emitting carbon dioxide affect the price dynamics of the European equity markets. The author uses the Vector Autoregressive (VAR) and Vector Error Correction (VECM) models in four specifications to investigate the linkages between the EUA market and major stock indexes of 27 EU countries which are participating in the second phase of the European Emissions Trading System. The regression models, together with Granger causality testing, suggest that stock markets of several developed European countries exhibit significant negative responses to EUA price shocks. In particular, CAC 40 (France), DAX 30 (Germany), AEX (the Netherlands), and FTSE MIB (Italy) indexes have been found to react to the EUA market movements. This may serve as a hint for the growing importance of the price of carbon as an additional risk factor for businesses given that emission quotas are being consistently tightened every year. Author: Andrii Shekhirev Supervisor: Cristian Huse Discussant: Huizi Zeng Date of Presentation: June 13th, 2011 Final Thesis: June 20th, 2011 Keywords: emissions trading, carbon markets, market linkages, ETS, price shocks, vector autoregression, VAR, Granger causality *[email protected] Andrii Shekhirev Effects of Carbon Pricing on EU Equity Markets Table of Contents 1. Introduction ......................................................................................................................... -

2015 Registration Document | 02
2015 REGISTRATION DOCUMENT | 02 CONTENTS Risks 2 5 Operating and fi nancial review 75 Strategic Risks 3 5.1 Overview 76 Financial Risks 5 5.2 Material contracts and related party Operational Risks 6 Transactions 96 5.3 Legal Proceedings 98 5.4 Insurance 100 Presentation of the Group 9 1 5.5 Liquidity and Capital Resources 101 1.1 Company Profi le 10 5.6 Tangible Fixed Assets 102 1.2 Strategy 12 1.3 Description of the Business 13 Financial Statements 103 1.4 Regulation 25 6 6.1 Consolidated Income Statement 104 6.2 Consolidated Statement Corporate Governance 29 2 of Comprehensive Income 105 2.1 Corporate Governance 30 6.3 Consolidated Balance Sheet 106 2.2 Management & Control Structure 32 6.4 Consolidated Statement of Cash Flows 107 2.3 Report of the Supervisory Board 43 6.5 Consolidated Statement of Changes 2.4 Remuneration report 45 in Parent’s Net Investment 2.5 Corporate Social Responsibility 50 and Shareholders’ Equity 108 6.6 Notes to the Consolidated Financial Statements 110 3 Selected historical combined fi nancial 6.7 Euronext N.V. Company Financial Statements information and other fi nancial for the year ended 31 December 2015 151 information 57 6.8 Notes to Euronext N.V. Financial Statements 153 6.9 Other information 167 4 General description of the Company and its share capital 61 Glossary 169 4.1 Legal Information on the Company 62 G 4.2 Share Capital 62 4.3 Shareholder structure 64 4.4 Share Classes and Major Shareholders 64 4.5 General Meeting of Shareholders and Voting Rights 69 4.6 Anti-Takeover Provisions 70 4.7 Obligations of Shareholders and Members of the Managing Board to Disclose Holdings 70 4.8 Short Positions 71 4.9 Market Abuse Regime 72 4.10 Transparency Directive 72 4.11 Dutch Financial Reporting Supervision Act 73 4.12 Dividends and Other Distributions 73 4.13 Financial Calendar 74 - 2015 Registration document 2015 Registration Document including the Annual Financial Report Euronext N.V.