DOCSLIB.ORG

Salam-The Physicist

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Salam-The Physicist Salam-the physicist November 21, 2012 Salam-the physicist Modern Physics: 1900-1940s Black body radiation: 2 dρ ≈ ν dν (Classically) 3 ν dν 0 dρ ≈ (Planck s result) eβν − 1 Energy is quantized! ⇒ Quantum theory Salam-the physicist Michelson-Morley experiment ⇓ Einsten’s special theory of relativity (1905) Time dilation, length contraction Salam-the physicist 2 E = m c Salam-the physicist Einstein’s general theory of relativity (1915) Gravity is the curvature of spacetime! Salam-the physicist Electron, Proton, Neutron, Muon, Photon Electromagnetic force (mediated by photon) Strong Nuclear force (keeps the protons in the nucleus, thought to be mediated by mesons) Salam-the physicist Schr¨odinger’s non-relativistic equation to Dirac Equation 2 ∂ψ ~ 2 i~ = − ∇ + V ψ ∂t 2m ↓ ∂ψ i~ = i~ ~α · ∇~ + V ψ ∂t Dirac equation predicted the existence of the antiparticle of electron Positron was found in 1932 Beginning of Quantum Field Theory (which can deal with arbitrary number of particles and antiparticles at the same time) Salam-the physicist The theory of light and matter (Photons and electrons/positrons): Quantum Electrodynamics 1 2 L = ψ¯ i6∂ − m ψ − F − eψ¯6A ψ 4 interaction electrons/positrons photons | {z } |{z} | {z } Salam-the physicist Probability of such processes ∼ ∞ Salam-the physicist p − k pk p 4 m Σ(p) d k Z k2(k − p)2 Correction to the mass of the electron: m 7→ m + δm Λ2 δm ∼ log 2 m Mass renormalization mphy = m + δm Breakdown of the theory? Salam-the physicist Renormalization of QED Freeman Dyson Salam-the physicist Overlapping divergences Salam-the physicist PHYSICAL REVIEW VOLUM E 82, NUM B ER 2 APRIL 15. i9$1 Overlapping Divergences anti the S-Matrix AaDUs SCRAM SI. Jobe's College, Cambridge, England {Received September 29, 1950) By extending considerations given by Dyson, general rules are obtained for isolating divergent parts from integrals corresponding to overlapping graphs, and a proof is obtained for the appearance of an extra factor ZI I from "b divergences. " In the last section the possibility of renormalization for scalar meson- nucleon interactions is demonstrated. L INTRODUCTION vertex u or b of Fig. 1. Here N his treatment of spinor electrodynamics Dyson' - ~ has de6ned operators A„, Z*, and II* corresponding Z (W2q p) o dtldtoFo(pi ti)Geo(pq tl) to)Hv(p) to)) (1) to the three types of primitive divergent graphs in the theory. In the calculation of the contribution to F„ where 1 — —o. arising from a reducible vertex part Vg it is possible to iy(p ti) F ti)= —V. break down unambiguously into an irreducible (p Vg tio (p —t,)'+ ~o vertex part plus various inserted self-energy (5) and vertex (V) parts. The divergences introduced by the zy(p ti to)— — latter can be removed in a well-dehned manner because G„„(p,ti, to) = 7„7„,—ti —to)'+ 2 any two of the insertions made in Vz are either com- (p pletely non-overlapping or else are so arranged that one iy(p t ) «—1— is completely contained in the other. This procedure H.(p, to) = fails, however, in the calculation of the contributions (p —to)'+ o' to' to Z* or II* from reducible self-energy graphs. Con- Not only is the double integral over t&t2 linearly diver- sidering, for example, the electron self-energy, there is gent, but it also diverges logarithmically if the integra- just one irreducible graph W, (Fig. 1). V parts inserted tion is performed over either tj or t2, while the other at one of the two end vertices u or b appear simultane- variable is held fixed. In order to isolate these diver- ously as vertex insertions at the other vertex. Corre- gences, we use (here and in the subsequent work) the spondingly, the contribution to Z* arising from a invariant separation procedure outlined in Sec. VI of reducible part 8'g is, in general, an integral which D involves divergences corresponding to each of the ways II. Rewrite as follows: in which 8'z might have been built up by insertion of Eq. (1) V parts at either or both vertices of lV~. Dyson has =o called these "b-divergences" and their expected effect z(Wog p) J J dtldtzLFo(p) tl)Gyo(p) tiq tz)Hy(pq tz) is appearance of an extra factor Zi ' in his Eqs. (88) and (89). In order to demonstrate the possibility of Fo(po ti)Go(p—o ti 0)& (P t) renormalization, it is vital that this factor should appear; and it is the purpose of this paper to attempt a F„(P,ti)G„„(po—, 0, to)P„(po, tz) 7 formal proof. The considerations presented here throw some on the of renormalization for ~' light prospects +e'~ dtiF„(po) ti)G.o(po, ti, 0) I scalar electrodynamics. EJ ) II. SEPARATION OF OVERLAPPING DIVERGENCES ~dt, X( tdta„(p, t,) (+. ( F„(p, t,) ) Dyson' (unpublished) has defined a formal mathe- ) E~ ) matical procedure for the isolation of the divergent t' part from an integral representing overlapping diver- I X dtZG. o(PO& 01& tz)&~(PO& tz) ~& (2) gent graphs. This procedure is illustrated most readily ~ by an example. Figure 2 represents an electron self-energy graph could be obtained the insertion of a V at / which by part / / / / I ' F. Dyson, Phys. Rev. 75, 1736 {1949},referred to as D II, I J. I \ in this paper. o ' The only published calculation for an integral corresponding to an overlapping {fourth order} graph is that of R. Jost and J. M. Luttinger, Helv. Phys. Acta 23, 201 {1949), who have followed Dyson's procedure. FIG. 1. Salam received Cambridge university’s Smith prize Salam-the physicist Neutrinos and parity violation 1 Neutrinos are spin 2 particles which interact very weakly with other particles They carry no charge and therefore do not feel the electromagnetic force Neutron 7→ Proton + Electron + Neutrino Postulated by Wolfgang Pauli in 1930 Salam-the physicist Neutrinos were detected in 1956 (Reined and Cowan at Hanford, WA) Salam-the physicist Parity : (x, y, z) 7→ (−x, −y, −z) It was believed that fundamental laws are invariant under parity transformation. Salam-the physicist In 1956 T. D. Lee and C. N. Yang postulated that parity is violated weak interactions (kind of interactions neutrinos were involved in) Salam-the physicist Around the same time (1956) Salam was also thinking about parity and its possible relation to the masslessness of the neutrino (there was no good reason for the neutrinos to me massless) In late 1956 he related the masslessness of the neutrino with the parity violation and wrote a preprint on it Discouraged by Pauli Salam did not publish the result until late 1957. Salam-the physicist Parity violation was found in beta decay experiments in January 1957. Salam-the physicist Salam-the physicist Supersymmetry and superspace The four fundamental forces: Electromagnetism, Weakforce, Electroweak force Strong force, Gravity | {z } The theory (theories) that combines Electroweak and the Strong force is called Grand Unified Theory The theory that combines all four forces is called Theory of Everything Salam-the physicist We live in a space whihc has three space dimensions and one time dimension. The space dimensions can be rotated into each other x cosθ sinθ x 7→ y −sinθ cosθ y Salam-the physicist Even time and spacce can be rotated into each other (special relativity) ct coshθ sinhθ ct 7→ x sinhθ coshθ x Time dilation, length contraction and other phenomena which occur at high speed are consequence of such a ”rotation” Salam-the physicist Supersymmetry suggest that there are other fermionic ”dimensions” which are measured by quantities η1, η2 These mysterious numbers which are coordinates in the fermionic directions have the property: 2 2 η1 = 0 , η2 == 0 η1η2 = −η2η1 Salam-the physicist Supersymmetry is a symmetry which rotates x, y, z, t, η1, η2 into each other As a consequence of this symmetry particles come in pairs (A, B) 1 such that the spin of the two particle A and B differs by 2 . Photon has a superpartner photino quarks have squarks electron has selectron Salam-the physicist With John Strathdee as a collaborator Salam wrote many papers on supersymmetry. A specially influential paper was ”Supersymmetry and Superfields” Fortsch. Phys. 26, 57-142 (1978) Salam-the physicist In this paper they developed the idea of a superfield: f (x, y, z, t) 7→ Φ(x, y, z, t, η)= φ0(x, y, z, t)+ η φ1(x, y, z, t) Salam-the physicist Scientific Writings — Abdus Salam home → abdus salam → bibliography → papers Timeline Bibliography Scientific Writings Books Biographies Papers Speeches Clippings Awards Recollections 1943 A Problem of Ramanujam. Links (Fourth Year Student, Government College, Lahore) . Marie Curie Library Math. Student XI, nos.1-2, 50-51 (1943). ICTP Home ICTP Portal 1950 Differential Identities in Three-Field Renormalization Problem. Phys. Rev. 79, 910-911 (1950). 1951 Release date: Divergent Integrals in Renormalizable Field Theories. 19 September 2011 Phys. Rev. 84, 426-431 (1951). - Download the promo (mp4) - Overlapping Divergences and the S-matrix. Phys. Rev. 82, 217-227 (1951). The Renormalization of Meson Theories. (with P.T. Matthews). Rev. Mod. Phys. 23, 311-314 (1951). 1952 The Intermediate Coupling Theory of the Pseudoscalar Meson-Nucleon Interaction. (with P.T. Matthews). Phys. Rev. 86, 715-726 (1952). Recent Advances in Nuclear Theory and Experiment. Pak. J. Sci. 4, no.1, 4-10 (1952). Renormalization of Scalar Electrodynamics Using β-Formalism. Proc. Roy. Soc. (London) A211, 276-284 (1952). Renormalized S-Matrix for Scalar Electrodynamics. Phys. Rev. 86, 731-744 (1952). 1953 Cosmological Theory.
Load more

Recommended publications
  • Department of Physics and Astronomy 1
    Department of Physics and Astronomy 1 PHSX 216 and PHSX 236, provide a calculus-based foundation in Department of Physics physics for students in physical science, engineering, and mathematics. PHSX 313 and the laboratory course, PHSX 316, provide an introduction and Astronomy to modern physics for majors in physics and some engineering and physical science programs. Why study physics and astronomy? Students in biological sciences, health sciences, physical sciences, mathematics, engineering, and prospective elementary and secondary Our goal is to understand the physical universe. The questions teachers should see appropriate sections of this catalog and major addressed by our department’s research and education missions range advisors for guidance about required physics course work. Chemistry from the applied, such as an improved understanding of the materials that majors should note that PHSX 211 and PHSX 212 are prerequisites to can be used for solar cell energy production, to foundational questions advanced work in chemistry. about the nature of mass and space and how the Universe was formed and subsequently evolved, and how astrophysical phenomena affected For programs in engineering physics (http://catalog.ku.edu/engineering/ the Earth and its evolution. We study the properties of systems ranging engineering-physics/), see the School of Engineering section of the online in size from smaller than an atom to larger than a galaxy on timescales catalog. ranging from billionths of a second to the age of the universe. Our courses and laboratory/research experiences help students hone their Graduate Programs problem solving and analytical skills and thereby become broadly trained critical thinkers. While about half of our majors move on to graduate The department offers two primary graduate programs: (i) an M.S.
    [Show full text]
  • Inspec Archive - List of Journals Covered Between 1898 and 1968
    February 2006 www.iee.org/inspec Inspec Archive - List of Journals Covered between 1898 and 1968 Abhandlungen der Berlin Akademie Acta Universitatis Lundensis. Sectio II. Medica, Abhandlungen der Braunschweigischen Mathematica, Scientiae Rerum Naturalium Wissenschaftlichen Gesellschaft Acta Universitatis Tamperensis Abhandlungen der Deutschen Akademie der Acustica Wissenschaften zu Berlin, Klasse fur Advanced Energy Conversion Mathematik, Physik und Technik Advances in Atomic and Molecular Physics Abhandlungen der Konigliches Preussisches Advances in Electronics Meteorologies Institut Advances in Physics Abhandlungen der Preussischen Akademieder Advances in Theoretical Physics Wissenschaften Advances of Science Accademia delle Scienze, Medico e Naturali, AEG Mitteilungen Ferrara AEG Progress ACEC Journal AEG Zeitung ACEC Review AEI Engineering Acero y Energia AEI Engineering Review Acta Academiae Aboensis, Mathematical AEI Journal of Telecommunications Physics AEI Research Laboratory Reports Acta and Commentationes Universitatis Aerial Age Tartuensis (Dorpatensis) Aerial Age Weekly Acta Automatica Sinica Aeronautical Engineering Review Acta Bolyaiana Aeronautical Journal Acta Chemica Scandinavica Aeronautical Research Council Current Papers Acta Crystallographica Aeronautical Research Council Reports and Acta Electronica Memoranda Acta Electronica Sinica Aeronautics Acta Geophysica Sinica Aeroplane Acta Mathematica Aerospace Engineering Acta Mathematica Sinica Agricultural and Horticultural Engineering Acta Mechanica Abstracts Acta Medica
    [Show full text]
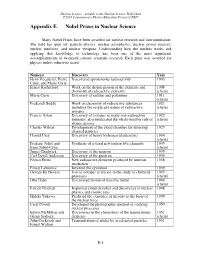
  • Appendix E Nobel Prizes in Nuclear Science
    Nuclear Science—A Guide to the Nuclear Science Wall Chart ©2018 Contemporary Physics Education Project (CPEP) Appendix E Nobel Prizes in Nuclear Science Many Nobel Prizes have been awarded for nuclear research and instrumentation. The field has spun off: particle physics, nuclear astrophysics, nuclear power reactors, nuclear medicine, and nuclear weapons. Understanding how the nucleus works and applying that knowledge to technology has been one of the most significant accomplishments of twentieth century scientific research. Each prize was awarded for physics unless otherwise noted. Name(s) Discovery Year Henri Becquerel, Pierre Discovered spontaneous radioactivity 1903 Curie, and Marie Curie Ernest Rutherford Work on the disintegration of the elements and 1908 chemistry of radioactive elements (chem) Marie Curie Discovery of radium and polonium 1911 (chem) Frederick Soddy Work on chemistry of radioactive substances 1921 including the origin and nature of radioactive (chem) isotopes Francis Aston Discovery of isotopes in many non-radioactive 1922 elements, also enunciated the whole-number rule of (chem) atomic masses Charles Wilson Development of the cloud chamber for detecting 1927 charged particles Harold Urey Discovery of heavy hydrogen (deuterium) 1934 (chem) Frederic Joliot and Synthesis of several new radioactive elements 1935 Irene Joliot-Curie (chem) James Chadwick Discovery of the neutron 1935 Carl David Anderson Discovery of the positron 1936 Enrico Fermi New radioactive elements produced by neutron 1938 irradiation Ernest Lawrence
    [Show full text]
  • Report from Trieste: ICTP on the March Why Have More Than 22 000 Scientists Studied at the International Centre for Theoretical Physics? by Akhtar Mahmud Faruqui
    Special reports Report from Trieste: ICTP on the march Why have more than 22 000 scientists studied at the International Centre for Theoretical Physics? by Akhtar Mahmud Faruqui A small Roman town under the Caesars, an indepen- responsibility to continue this flow of benefits to society dent municipality in the Middle Ages, a flourishing and, most important, to extend them to the very large international port and trading centre between the West fraction of the world's burgeoning populations that have and East after 1700, and an Italian entity since 1918, thus far — for whatever reason — been denied them," Trieste is a city of entrancing scenic attractions. Tucked D. Allan Bromley has noted.* The report, Physics in away in the northeast of Italy on the Adriatic Sea, the Perspective, strengthens Saiam and Bromley's view: city stands on tree-dotted hills resembling a sunlit sea- "Science is knowing. What man knows about inanimate washed amphitheatre, with the surrounding Carso nature is physics, or rather the most lasting and univer- plateau rated as one of the most enchanting landscapes sal things that he knows make up physics. As he gains in Europe. more knowledge, what would have appeared compli- But Trieste is now known not just for its scenic splen- cated or capricious can be seen as essentially simple and dours or past grandeurs. It is identified increasingly as in a deep sense orderly. And, to understand how things a meeting place of bright scientific minds from the West work is to see how, within environmental constraints and the East, from the North and the South.
    [Show full text]
  • A Model for Free Will and Destiny- Part One
    International Journal of Scientific and Research Publications, Volume 2, Issue 8, August 2012 1 ISSN 2250-3153 OF ESCHATOLOGICAL DOXIES AND HAUBERK HAUTEUR- A MODEL FOR FREE WILL AND DESTINY- PART ONE 1DR K N PRASANNA KUMAR, 2PROF B S KIRANAGI AND 3 PROF C S BAGEWADI Abstract: Ising model with $h\neq 0$, where the relation with gauge theory is used to discuss the phenomenon of confinements is firmly established on terra firma. It has been concluded by many Physicists that quantum spin diffusion in one dimensional chains and a presentation of the chiral potts model which illustrates the physical effects that can occur when the Euclidean and Minkowski regions and they are not connected by an analytic continuation. We state that when Euclidian and Minkowski regions are combined together many interesting results that could have wide ranging amplitudinal ramifications with perceptual field and perceiving object could be studied and thrown light upon. Consciousness distinction with unconsciousness and temporal superposition of latent intents and manifest actions(See Robert Merton) is another example that may provide bewildering results ,notwithstanding the fact we have not approached with ―open mind‖.Nonequilibrium statistical mechanics and its concomitant primary order and secondary organization with quantum field has been studied and investigated by takafumi kita where a conception, creation, process oriented and system oriented a concise and self-contained introduction to non equilibrium statistical mechanics with quantum field theory by considering an ensemble of interacting identical bosons or fermions as an example. An analogue can be seen in verbal proliferation, visual representation and expressible sense for they are essentially process oriented and system proclivitisied.
    [Show full text]
  • Main Attributes of Nuclides Presented in This Book
    Appendix A Main Attributes of Nuclides Presented in This Book Data given in TableA.1 can be used to determine the various decay energies for the specific radioactive decay examples as well as for the nuclear activation examples presented in this book. M stands for the nuclear rest mass; M stands for the atomic rest mass. The data were obtained from the NIST and are based on CODATA 2010 as follows: 1. Data for atomic masses M are given in atomic mass constants u and were obtained from the NIST at: (http://www.physics.nist.gov/pml/data/comp.cfm). 2. Rest mass of proton mp, neutron mn, electron me, and of the atomic mass constant u are from the NIST (http://www.physics.nist.gov/cuu/constants/index. html) as follows: −27 2 mp = 1.672 621 777×10 kg = 1.007 276 467 u = 938.272 046 MeV/c (A.1) −27 2 mn = 1.674 927 351×10 kg = 1.008 664 916 u = 939.565 379 MeV/c (A.2) −31 −4 2 me = 9.109 382 91×10 kg = 5.485 799 095×10 u = 0.510 998 928 MeV/c (A.3) − 1u= 1.660 538 922×10 27 kg = 931.494 060 MeV/c2 (A.4) 3. For a given nuclide, its nuclear rest energy was determined by subtracting the 2 rest energy of all atomic orbital electrons (Zmec ) from the atomic rest energy M(u)c2 as follows 2 2 2 Mc = M(u)c − Zmec = M(u) × 931.494 060 MeV/u − Z × 0.510 999 MeV.
    [Show full text]
  • Detection of Black Holes
    ehind t b h y e r s c o c Detection of Black Holes t t i i e e s s n n e e c c The Power of Robust Theory and Mathematics h h e e T T Albert Einstein Black holes stir the mind to the heights of imagination. publication of the General Theory in 1915, scientists toying What do these gravitational wells from which light cannot with the limits of Relativity Theory realized the very weird escape look like? Does speaking of them as being visible possibilities that arose. The prediction and acceptance of even make sense? And if we can't see them, how would black holes hinged on interpreting the predictions of we locate them? The greatest scientific minds have Einstein's Relativity Theory. struggled to understand black holes over the past century. In the face of many towering challenges, they now better understand these strange phenomena. Black holes are 1. In many cases, theories are incomplete at their bizarre, but they still appear to follow the laws of physics. birth. When first conceived, all scientific knowledge has a speculative character. As this This story describes how scientists have studied and story illustrates, much time usually passes before detected black holes throughout the last century. Because ideas are rejected or accepted by the scientific black holes embody the most extreme physics in the community. The theories of relativity, like all good Universe, significant efforts were required to understand scientific theories, explain natural phenomena, and accept what theory had predicted. Most scientists had bring coherence to a field of study, and suggest to overcome a sort of instinctual defense that told them research questions worth pursuing, how to go such a weird object could not possibly exist in our about answering those questions, and how to Universe.
    [Show full text]
  • List of Journals
    Revised 29 March 2005 www.iee.org/inspec List of Journals Journal names prefixed with * are abstracted completely. Journal names prefixed with † are electronic-only publications. *(AI EDAM) Artificial Intelligence for Engineering *Acoustics Bulletin Design, Analysis and Manufacturing *Acoustics Research Letters Online 73 Amateur Radio Today Acquisitions Librarian AAVSO Circular *Acta Acustica ABA Bank Marketing *Acta Acustica United With Acustica ABA Banking Journal *Acta Astronomica ABB Review *Acta Astrophysica Sinica ABI-Technik *Acta Automatica Sinica Abstract and Applied Analysis *Acta Crystallographica, Section A (Foundations of *ABU Technical Review Crystallography) †Academic Open Internet Journal Acta Crystallographica, Section B (Structural Science) Academic Radiology Acta Crystallographica, Section C (Crystal Structure Academic Reports, Faculty of Engineering, Tokyo Communications) Institute of Polytechnics *Acta Crystallographica, Section D (Biological Academie des Sciences. Comptes Rendus, Crystallography) Mathematique †Acta Crystallographica, Section E (Structure Reports Academie des Sciences. Comptes Rendus, Physique Online) Academie Serbe des Sciences et des Arts Bulletin, *Acta Cybernetica Classe des Sciences Techniques *Acta Electronica Sinica Academie Serbe des Sciences et des Arts, Glas, Classe Acta Graphica des Sciences Techniques *Acta Informatica Academy of Management Journal Acta Manilana Academy of Management Review *Acta Materialia Accountancy Acta Mathematica Sinica Accounting Organizations and Society Acta Mathematicae
    [Show full text]
  • PROPOSAL for a Ph.D. in APPLIED and COMPUTATIONAL PHYSICS Department of Physics College of Arts and Sciences Requested Program I
    PROPOSAL FOR A Ph.D. in APPLIED AND COMPUTATIONAL PHYSICS Department of Physics College of Arts anD Sciences Requested Program Implementation Term: Fall 2019 College of Arts anD Sciences Governance CAS GraDuate Committee on Instruction Date Submitted: March 1, 2010 Date Approved: January 13, 2011 CAS Assembly Date Submitted: February 1, 2011 Date Approved: March 15, 2011 University Governance GraDuate Council Date Submitted: March 30, 2011 Date Approved: December 5, 2011 Senate Date Submitted: January 2012 Date Approved: May 10, 2012 BoarD of Trustees Date Submitted Date Approved PresiDents Council Date Submitted Date Approved PROPOSAL FOR A Ph.D. in APPLIED AND COMPUTATIONAL PHYSICS Submitted by The Department of Physics January 29, 2010 Revised October 24, 2018 1 SUMMARY This catalog presents a proposal to create a Ph.D. degree, in the Department of Physics at Oakland University, in Applied and Computational Physics. The desired start date is the 2019 Fall Semester. In recent years, the Physical Sciences were recognized as extremely important for the economic development of the Unites States. The Department of Physics at Oakland University is amply prepared to take advantage of new opportunities and proposes an attractive PhD program in Applied and Computational Physics. Along the years, the consistent federal funding obtained by the non-medical physics members of the Department points to the high level of their research. New talented PhD students will further strengthen the faculty research; therefore, the new program promises to be highly beneficial for Oakland University. In addition, the possibility of training Ph.D. students in specialized areas of research is a fundamental part in the development of any natural sciences department.
    [Show full text]
  • Guide to the Subrahmanyan Chandrasekhar Papers 1913-2011
    University of Chicago Library Guide to the Subrahmanyan Chandrasekhar Papers 1913-2011 © 2006 University of Chicago Library Table of Contents Descriptive Summary 3 Information on Use 3 Access 3 Citation 3 Biographical Note 4 Scope Note 5 Related Resources 9 Subject Headings 9 INVENTORY 10 Series I: Personal Correspondence and Papers 10 Subseries 1: Biographical materials and personal papers 10 Subseries 2: Personal correspondence 12 Series II: Scientific Correspondence 20 Series III: Scientific Writings 45 Series IV: Lecture Notes 122 Subseries 1: Cambridge University notes 122 Subseries 2: University of Chicago Notes 124 Subseries 3: Special lectures 130 Series V: Astrophysical Journal Records 134 Series VI: Articles by Colleagues 136 Subseries 1: Offprints 136 Subseries 2: Typescripts 136 Series VII: Addenda 137 Subseries 1: Personal and Biographical 140 Sub-subseries 1: General personal and biographical papers 140 Sub-subseries 2: Personal correspondence 154 Sub-subseries 3: Publications 158 Sub-subseries 4: Chandra X-Ray Observatory 163 Subseries 2: Correspondence 164 Subseries 3: Writing 193 Subseries 4: Writings about Chandrasekhar 223 Subseries 5: Writings by others 229 Subseries 6: Audiovisual 239 Sub-subseries 1: Photographic material 239 Sub-subseries 2: Audio 267 Sub-subseries 3: Video 275 Subseries 7: Oversize 276 Subseries 8: Artifacts and framed items 292 Subseries 9: Medals 295 Subseries 10: Restricted 297 Sub-subseries 1: Administrative records and referee’s reports 297 Sub-subseries 2: Financial records 297 Sub-subseries 3: Letters of recommendation for colleagues and faculty appointment301 material Sub-subseries 4: Student grades and letters of recommendation 305 Descriptive Summary Identifier ICU.SPCL.CHANDRASEKHAR Title Chandrasekhar, Subrahmanyan.
    [Show full text]
  • The Sudden Selector's Guide to Physics Resources
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Purdue E-Pubs Purdue University Purdue e-Pubs Libraries Faculty and Staff choS larship and Research Purdue Libraries 2013 The uddeS n Selector's Guide to Physics Resources Michael Fosmire Purdue University, [email protected] Follow this and additional works at: http://docs.lib.purdue.edu/lib_fsdocs Recommended Citation Fosmire, Michael, "The uddeS n Selector's Guide to Physics Resources" (2013). Libraries Faculty and Staff Scholarship and Research. Paper 57. http://docs.lib.purdue.edu/lib_fsdocs/57 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. Sudden Selector’s Guide to Physics Resources ALCTS/CMS SUDDEN SELECTOR’S SERIES Sudden Selector’s Guide to Business Resources Sudden Selector’s Guide to Communication Studies Resources Sudden Selector’s Guide to Chemistry Resources Sudden Selector’s Guide to Biology Resources Sudden Selector’s Guide to Physics Resources ALCTS/CMS SUDDEN SELECTOR’S SERIES, #5 SUDDEN SELECTOR’S GUIDE to Physics Resources MICHAEL FOSMIRE Helene Williams, Series Editor Collection Management Section of the Association for Library Collections & Technical Services a division of the American Library Association Chicago 2013 While extensive effort has gone into ensuring the reliability of information appearing in this book, the publisher makes no warranty, express or implied, on the accuracy or reliability of the information, and does not assume and hereby disclaims any liability to any person for any loss or damage caused by errors or omissions in this publication.
    [Show full text]
  • Cosmic Anger : Abdus Salam
    COSMIC ANGER This page intentionally left blank COSMIC ANGER Abdus Salam – the fi rst Muslim Nobel scientist by Gordon Fraser 1 3 Great Clarendon Street, Oxford OX2 6DP Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide in Oxford New York Auckland Cape Town Dar es Salaam Hong Kong Karachi Kuala Lumpur Madrid Melbourne Mexico City Nairobi New Delhi Shanghai Taipei Toronto With offi ces in Argentina Austria Brazil Chile Czech Republic France Greece Guatemala Hungary Italy Japan Poland Portugal Singapore South Korea Switzerland Thailand Turkey Ukraine Vietnam Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries Published in the United States by Oxford University Press Inc., New York © Gordon Fraser 2008 The moral rights of the author have been asserted Database right Oxford University Press (maker) First published 2008 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above You must not circulate this book in any other binding or cover and you must impose the same condition on any acquirer British Library Cataloguing in Publication Data Data available Library of Congress Cataloging in Publication Data Data available Typeset by Newgen Imaging Systems (P) Ltd., Chennai, India Printed in Great Britain on acid-free paper by Biddles Ltd., www.biddles.co.uk ISBN 978–0–19–920846–3 (Hbk.) 1 3 5 7 9 10 8 6 4 2 Contents List of illustrations vi Introduction vii Acknowledgements and sources ix Author’s note xii 1.
    [Show full text]