DOCSLIB.ORG

3. Cross Product Definition 3.1. Let V and W Be Two Vectors in R 3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
3. Cross Product Definition 3.1. Let V and W Be Two Vectors in R 3 3. Cross product Definition 3.1. Let ~v and ~w be two vectors in R3. The cross product of ~v and ~w, denoted ~v × ~w, is the vector defined as follows: • the length of ~v × ~w is the area of the parallelogram with sides ~v and ~w, that is, k~vkk~wk sin θ. • ~v × ~w is orthogonal to both ~v and ~w. • the three vectors ~v, ~w and ~v × ~w form a right-handed set of vectors. Remark 3.2. The cross product only makes sense in R3. Example 3.3. We have ^{ × |^ = k;^ |^× k^ = ^{ and k^ × ^{ =|: ^ By contrast |^× ^{ = −k;^ k^ × |^ = −^{ and ^{ × k^ = −|:^ Theorem 3.4. Let ~u, ~v and ~w be three vectors in R3 and let λ be a scalar. (1) ~v × ~w = −~w × ~v. (2) ~u × (~v + ~w) = ~u × ~v + ~u × ~w. (3) (~u + ~v) × ~w = ~u × ~w + ~v × ~w. (4) λ(~v × ~w) = (λ~v) × ~w = ~v × (λ~w). Before we prove (3.4), let's draw some conclusions from these prop- erties. Remark 3.5. Note that (1) of (3.4) is what really distinguishes the cross product (the cross product is skew commutative). Consider computing the cross product of ^{, ^{ and| ^. On the one hand, (^{ × ^{) × |^ = ~0 × ~j = ~0: On the other hand, ^{ × (^{ × |^) = ^{ × k^ = −|:^ In other words, the order in which we compute the cross product is important (the cross product is not associative). Note that if ~v and ~w are parallel, then the cross product is the zero vector. One can see this directly from the formula; the area of the parallelogram is zero and the only vector of zero length is the zero 1 vector. On the other hand, we know that ~w = λ~v. In this case, ~v × ~w = ~v × (λ~v) = λ~v × ~v = −λ~v × ~v: To get from the second to the third line, we just switched the factors. But the only vector which is equal to its inverse is the zero vector. Let's try to compute the cross product using (3.4). If ~v = (v1; v2; v3) and ~w = (w1; w2; w3), then ^ ^ ~v × ~w = (v1^{ + v2|^+ v3k) × (w1^{ + w2|^+ w3k) ^ = v1w1(^{ × ^{) + v1w2(^{ × |^) + v1w3(^{ × k) ^ + v2w1(^| × ^{) + v2w2(^| × |^) + v2w3(^| × k) ^ ^ ^ ^ + v3w1(k × ^{) + v3w2(k × |^) + v3w3(k × k) ^ = (v2w3 − v3w2)^{ + (v3w1 − v1w3)^| + (v1w2 − v2w1)k: Definition 3.6. A matrix A = (aij) is a rectangular array of numbers, where aij is in the i row and jth column. If A has m rows and n columns, then we say that A is a m × n matrix. Example 3.7. −2 1 −7 a a a A = = 11 12 13 ; 0 2 −4 a21 a22 a23 is a 2 × 3 matrix. a23 = −4. Definition 3.8. If a b A = c d is a 2 × 2 matrix, then the determinant of A is the scalar a b = ad − bc: c d If 0a b c1 A = @d e fA g h i is a 3 × 3 matrix, then the determinant of A is the scalar a b c e f d f d e d e f = a − b + c : h i g i g h g h i 2 Note that the cross product of ~v and ~w is the (formal) determinant ^{ |^ k^ v1 v2 v3 : w1 w2 w3 Let's now turn to the proof of (3.4). Definition 3.9. Let ~u, ~v and ~w be three vectors in R3. The triple scalar product is (~u × ~v) · ~w. The triple scalar product is the signed volume of the parallelepiped formed using the three vectors, ~u, ~v and ~w. Indeed, the volume of the parallelepiped is the area of the base times the height. For the base, we take the parallelogram with sides ~u and ~v. The magnitude of ~u × ~v is the area of this parallelogram. The height of the parallelepiped, up to sign, is the length of ~w times the cosine of the angle, let's call this φ, between ~u × ~v and ~w. The sign is positive, if ~u, ~v and ~w form a right-handed set and negative if they form a left-handed set. Lemma 3.10. If ~u = (u1; u2; u3), ~v = (v1; v2; v3) and ~w = (w1; w2; w3) are three vectors in R3, then u1 u2 u3 (~u × ~v) · ~w = v1 v2 v3 : w1 w2 w3 Proof. We have already seen that ^{ |^ k^ ~u × ~v = u1 u2 u3 : v1 v2 v3 If one expands this determinant and dots with ~w, this is the same as replacing the top row by (w1; w2; w3), w1 w2 w3 (~u × ~v) · ~w = u1 u2 u3 : v1 v2 v3 Finally, if we switch the first row and the second row, and then the second row and the third row, the sign changes twice (which makes no change at all): u1 u2 u3 (~u × ~v) · ~w = v1 v2 v3 : w1 w2 w3 3 Example 3.11. The scalar triple product of ^{, |^ and k^ is one. One way to see this is geometrically; the parallelepiped determined by these three vectors is the unit cube, which has volume 1, and these vectors form a right-handed set, so that the sign is positive. Another way to see this is to compute directly (^{ × |^) · k^ = k^ · k^ = 1: Finally one can use determinants, 1 0 0 (^{ × |^) · k^ = 0 1 0 = 1: 0 0 1 Lemma 3.12. Let ~u, ~v and ~w be three vectors in R3. Then (~u × ~v) · ~w = (~v × ~w) · ~u = (~w × ~u) · ~v: Proof. In fact all three numbers have the same absolute value, namely the volume of the parallelepiped with sides ~u, ~v and ~w. On the other hand, if ~u, ~v, and ~w is a right-handed set, then so is ~v, ~w and ~u and vice-versa, so all three numbers have the same sign as well. Lemma 3.13. Let ~v and ~w be two vectors in R3. Then ~v = ~w if and only if ~v · ~x = ~w · ~x, for every vector ~x in R3. Proof. One direction is clear; if ~v = ~w, then ~v · ~x = ~w · ~x for any vector ~x. So, suppose that we know that ~v · ~x = ~w · ~x, for every vector ~x. Suppose that ~v = (v1; v2; v3) and ~w = (w1; w2; w3). If we take ~x = ^{, then we see that v1 = ~v · ^{ = ~w · ^{ = w1: Similarly, if we take ~x =| ^ and ~x = k^, then we also get v2 = ~v · |^ = ~w · |^ = w2; and ^ ^ v3 = ~v · k = ~w · k = w3: But then ~v = ~w as they have the same components. Proof of (3.4). We first prove (1). Both sides have the same magni- tude, namely the area of the parallelogram with sides ~v and ~w. Further both sides are orthogonal to ~v and ~w, so the only thing to check is the change in sign. 4 As ~v, ~w and ~v × ~w form a right-handed triple, it follows that ~w, ~v and ~v × ~w form a left-handed triple. But then ~w, ~v and −~v × ~w form a right-handed triple. It follows that ~w × ~v = −~v × ~w: This is (1). To check (2), we check that (~u × (~v + ~w)) · ~x = (~u × ~v + ~u × ~w) · ~x; for an arbitrary vector ~x. We first attack the LHS. By (3.12), we have (~u × (~v + ~w)) · ~x = (~x × ~u) · (~v + ~w) = (~x × ~u) · ~v + (~x × ~u) · ~w = (~u × ~v) · ~x + (~u × ~w) · ~x: We now attack the RHS. (~u × ~v + ~u × ~w) · ~x = (~u × ~v) · ~x + (~u × ~v) · ~x: It follows that both sides are equal. This is (2). We could check (3) by a similar argument. Here is another way. (~u + ~v) × ~w = −~w × (~u + ~v) = −~w × ~u − ~w × ~v = ~u × ~w + ~v × ~w: This is (3). To prove (4), it suffices to prove the first equality, since the fact that the first term is equal to the third term follows by a similar derivation. If λ = 0, then both sides are the zero vector, and there is nothing to prove. So we may assume that λ 6= 0. Note first that the magnitude of both sides is the area of the parallelogram with sides λ~v and ~w. If λ > 0, then ~v and λ~v point in the same direction. Similarly ~v × ~w and λ(~v × ~w) point in the same direction. As ~v, ~w and ~v × ~w for a right-handed set, then so do λ~v, ~w and λ(~v × ~w). But then λ(~v × ~w) is the cross product of λ~v and ~w, that is, (λ~v) × ~w = λ(~v × ~w): If λ < 0, then ~v and λ~v point in the opposite direction. Similarly ~v × ~w and λ(~v × ~w) point in the opposite direction. But then λ~v, ~w and λ(~v × ~w) still form a right-handed set. This is (4). 5.
Load more

Recommended publications
  • Research Brief March 2017 Publication #2017-16
    Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing
    [Show full text]
  • DERIVATIONS and PROJECTIONS on JORDAN TRIPLES an Introduction to Nonassociative Algebra, Continuous Cohomology, and Quantum Functional Analysis
    DERIVATIONS AND PROJECTIONS ON JORDAN TRIPLES An introduction to nonassociative algebra, continuous cohomology, and quantum functional analysis Bernard Russo July 29, 2014 This paper is an elaborated version of the material presented by the author in a three hour minicourse at V International Course of Mathematical Analysis in Andalusia, at Almeria, Spain September 12-16, 2011. The author wishes to thank the scientific committee for the opportunity to present the course and to the organizing committee for their hospitality. The author also personally thanks Antonio Peralta for his collegiality and encouragement. The minicourse on which this paper is based had its genesis in a series of talks the author had given to undergraduates at Fullerton College in California. I thank my former student Dana Clahane for his initiative in running the remarkable undergraduate research program at Fullerton College of which the seminar series is a part. With their knowledge only of the product rule for differentiation as a starting point, these enthusiastic students were introduced to some aspects of the esoteric subject of non associative algebra, including triple systems as well as algebras. Slides of these talks and of the minicourse lectures, as well as other related material, can be found at the author's website (www.math.uci.edu/∼brusso). Conversely, these undergraduate talks were motivated by the author's past and recent joint works on derivations of Jordan triples ([116],[117],[200]), which are among the many results discussed here. Part I (Derivations) is devoted to an exposition of the properties of derivations on various algebras and triple systems in finite and infinite dimensions, the primary questions addressed being whether the derivation is automatically continuous and to what extent it is an inner derivation.
    [Show full text]
  • Triple Product Formula and the Subconvexity Bound of Triple Product L-Function in Level Aspect
    TRIPLE PRODUCT FORMULA AND THE SUBCONVEXITY BOUND OF TRIPLE PRODUCT L-FUNCTION IN LEVEL ASPECT YUEKE HU Abstract. In this paper we derived a nice general formula for the local integrals of triple product formula whenever one of the representations has sufficiently higher level than the other two. As an application we generalized Venkatesh and Woodbury’s work on the subconvexity bound of triple product L-function in level aspect, allowing joint ramifications, higher ramifications, general unitary central characters and general special values of local epsilon factors. 1. introduction 1.1. Triple product formula. Let F be a number field. Let ⇡i, i = 1, 2, 3 be three irreducible unitary cuspidal automorphic representations, such that the product of their central characters is trivial: (1.1) w⇡i = 1. Yi Let ⇧=⇡ ⇡ ⇡ . Then one can define the triple product L-function L(⇧, s) associated to them. 1 ⌦ 2 ⌦ 3 It was first studied in [6] by Garrett in classical languages, where explicit integral representation was given. In particular the triple product L-function has analytic continuation and functional equation. Later on Shapiro and Rallis in [19] reformulated his work in adelic languages. In this paper we shall study the following integral representing the special value of triple product L function (see Section 2.2 for more details): − ⇣2(2)L(⇧, 1/2) (1.2) f (g) f (g) f (g)dg 2 = F I0( f , f , f ), | 1 2 3 | ⇧, , v 1,v 2,v 3,v 8L( Ad 1) v ZAD (FZ) D (A) ⇤ \ ⇤ Y D D Here fi ⇡i for a specific quaternion algebra D, and ⇡i is the image of ⇡i under Jacquet-Langlands 2 0 correspondence.
    [Show full text]
  • Vectors, Matrices and Coordinate Transformations
    S. Widnall 16.07 Dynamics Fall 2009 Lecture notes based on J. Peraire Version 2.0 Lecture L3 - Vectors, Matrices and Coordinate Transformations By using vectors and defining appropriate operations between them, physical laws can often be written in a simple form. Since we will making extensive use of vectors in Dynamics, we will summarize some of their important properties. Vectors For our purposes we will think of a vector as a mathematical representation of a physical entity which has both magnitude and direction in a 3D space. Examples of physical vectors are forces, moments, and velocities. Geometrically, a vector can be represented as arrows. The length of the arrow represents its magnitude. Unless indicated otherwise, we shall assume that parallel translation does not change a vector, and we shall call the vectors satisfying this property, free vectors. Thus, two vectors are equal if and only if they are parallel, point in the same direction, and have equal length. Vectors are usually typed in boldface and scalar quantities appear in lightface italic type, e.g. the vector quantity A has magnitude, or modulus, A = |A|. In handwritten text, vectors are often expressed using the −→ arrow, or underbar notation, e.g. A , A. Vector Algebra Here, we introduce a few useful operations which are defined for free vectors. Multiplication by a scalar If we multiply a vector A by a scalar α, the result is a vector B = αA, which has magnitude B = |α|A. The vector B, is parallel to A and points in the same direction if α > 0.
    [Show full text]
  • Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim, Jin Hyung Kim
    Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim, Jin Hyung Kim To cite this version: Dae Hwan Kim, Jin Hyung Kim. Ligature Modeling for Recognition of Characters Written in 3D Space. Tenth International Workshop on Frontiers in Handwriting Recognition, Université de Rennes 1, Oct 2006, La Baule (France). inria-00105116 HAL Id: inria-00105116 https://hal.inria.fr/inria-00105116 Submitted on 10 Oct 2006 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Ligature Modeling for Recognition of Characters Written in 3D Space Dae Hwan Kim Jin Hyung Kim Artificial Intelligence and Artificial Intelligence and Pattern Recognition Lab. Pattern Recognition Lab. KAIST, Daejeon, KAIST, Daejeon, South Korea South Korea [email protected] [email protected] Abstract defined shape of character while it showed high recognition performance. Moreover when a user writes In this work, we propose a 3D space handwriting multiple stroke character such as ‘4’, the user has to recognition system by combining 2D space handwriting write a new shape which is predefined in a uni-stroke models and 3D space ligature models based on that the and which he/she has never seen.
    [Show full text]
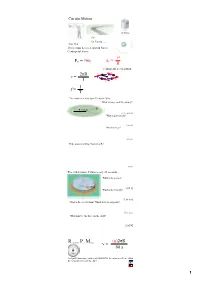
  • FC = Mac V2 R V = 2Πr T F = T 1
    Circular Motion Gravitron Cars Car Turning (has a curse) Rope Skip There must be a net inward force: Centripetal Force v2 F = maC a = C C R Centripetal acceleration 2πR v v v = R v T v 1 f = T The motorcycle rider does 13 laps in 150 s. What is his period? Frequency? R = 30 m [11.5 s, 0.087 Hz] What is his velocity? [16.3 m/s] What is his aC? [8.9 m/s2] If the mass is 180 kg, what is his FC? [1600 N] The child rotates 5 times every 22 seconds... What is the period? 60 kg [4.4 s] What is the velocity? [2.86 m/s] What is the acceleration? Which way does it point? [4.1 m/s2] What must be the force on the child? [245 N] Revolutions Per Minute (n)2πR v = 60 s An Ipod's hard drive rotates at 4200 RPM. Its radius is 0.03 m. What is the velocity in m/s of its edge? 1 Airplane Turning v = 232 m/s (520 mph) aC = 7 g's What is the turn radius? [785 m = 2757 ft] 2 FC Solving Circular Motion Problems 1. Determine FC (FBD) 2 2. Set FC = m v R 3. Solve for unknowns The book's mass is 2 kg it is spun so that the tension is 45 N. What is the velocity of the book in m/s? In RPM? R = 0.75 m [4.11 m/s] [52 RPM] What is the period (T) of the book? [1.15 s] The car is traveling at 25 m/s and the turn's radius is 63 m.
    [Show full text]
  • ISO Basic Latin Alphabet
    ISO basic Latin alphabet The ISO basic Latin alphabet is a Latin-script alphabet and consists of two sets of 26 letters, codified in[1] various national and international standards and used widely in international communication. The two sets contain the following 26 letters each:[1][2] ISO basic Latin alphabet Uppercase Latin A B C D E F G H I J K L M N O P Q R S T U V W X Y Z alphabet Lowercase Latin a b c d e f g h i j k l m n o p q r s t u v w x y z alphabet Contents History Terminology Name for Unicode block that contains all letters Names for the two subsets Names for the letters Timeline for encoding standards Timeline for widely used computer codes supporting the alphabet Representation Usage Alphabets containing the same set of letters Column numbering See also References History By the 1960s it became apparent to thecomputer and telecommunications industries in the First World that a non-proprietary method of encoding characters was needed. The International Organization for Standardization (ISO) encapsulated the Latin script in their (ISO/IEC 646) 7-bit character-encoding standard. To achieve widespread acceptance, this encapsulation was based on popular usage. The standard was based on the already published American Standard Code for Information Interchange, better known as ASCII, which included in the character set the 26 × 2 letters of the English alphabet. Later standards issued by the ISO, for example ISO/IEC 8859 (8-bit character encoding) and ISO/IEC 10646 (Unicode Latin), have continued to define the 26 × 2 letters of the English alphabet as the basic Latin script with extensions to handle other letters in other languages.[1] Terminology Name for Unicode block that contains all letters The Unicode block that contains the alphabet is called "C0 Controls and Basic Latin".
    [Show full text]
  • Form W-4, Employee's Withholding Certificate
    Employee’s Withholding Certificate OMB No. 1545-0074 Form W-4 ▶ (Rev. December 2020) Complete Form W-4 so that your employer can withhold the correct federal income tax from your pay. ▶ Department of the Treasury Give Form W-4 to your employer. 2021 Internal Revenue Service ▶ Your withholding is subject to review by the IRS. Step 1: (a) First name and middle initial Last name (b) Social security number Enter Address ▶ Does your name match the Personal name on your social security card? If not, to ensure you get Information City or town, state, and ZIP code credit for your earnings, contact SSA at 800-772-1213 or go to www.ssa.gov. (c) Single or Married filing separately Married filing jointly or Qualifying widow(er) Head of household (Check only if you’re unmarried and pay more than half the costs of keeping up a home for yourself and a qualifying individual.) Complete Steps 2–4 ONLY if they apply to you; otherwise, skip to Step 5. See page 2 for more information on each step, who can claim exemption from withholding, when to use the estimator at www.irs.gov/W4App, and privacy. Step 2: Complete this step if you (1) hold more than one job at a time, or (2) are married filing jointly and your spouse Multiple Jobs also works. The correct amount of withholding depends on income earned from all of these jobs. or Spouse Do only one of the following. Works (a) Use the estimator at www.irs.gov/W4App for most accurate withholding for this step (and Steps 3–4); or (b) Use the Multiple Jobs Worksheet on page 3 and enter the result in Step 4(c) below for roughly accurate withholding; or (c) If there are only two jobs total, you may check this box.
    [Show full text]
  • Vector Analysis
    DOING PHYSICS WITH MATLAB VECTOR ANANYSIS Ian Cooper School of Physics, University of Sydney [email protected] DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS cemVectorsA.m Inputs: Cartesian components of the vector V Outputs: cylindrical and spherical components and [3D] plot of vector cemVectorsB.m Inputs: Cartesian components of the vectors A B C Outputs: dot products, cross products and triple products cemVectorsC.m Rotation of XY axes around Z axis to give new of reference X’Y’Z’. Inputs: rotation angle and vector (Cartesian components) in XYZ frame Outputs: Cartesian components of vector in X’Y’Z’ frame mscript can be modified to calculate the rotation matrix for a [3D] rotation and give the Cartesian components of the vector in the X’Y’Z’ frame of reference. Doing Physics with Matlab 1 SPECIFYING a [3D] VECTOR A scalar is completely characterised by its magnitude, and has no associated direction (mass, time, direction, work). A scalar is given by a simple number. A vector has both a magnitude and direction (force, electric field, magnetic field). A vector can be specified in terms of its Cartesian or cylindrical (polar in [2D]) or spherical coordinates. Cartesian coordinate system (XYZ right-handed rectangular: if we curl our fingers on the right hand so they rotate from the X axis to the Y axis then the Z axis is in the direction of the thumb). A vector V in specified in terms of its X, Y and Z Cartesian components ˆˆˆ VVVV x,, y z VViVjVk x y z where iˆˆ,, j kˆ are unit vectors parallel to the X, Y and Z axes respectively.
    [Show full text]
  • Matrices and Tensors
    APPENDIX MATRICES AND TENSORS A.1. INTRODUCTION AND RATIONALE The purpose of this appendix is to present the notation and most of the mathematical tech- niques that are used in the body of the text. The audience is assumed to have been through sev- eral years of college-level mathematics, which included the differential and integral calculus, differential equations, functions of several variables, partial derivatives, and an introduction to linear algebra. Matrices are reviewed briefly, and determinants, vectors, and tensors of order two are described. The application of this linear algebra to material that appears in under- graduate engineering courses on mechanics is illustrated by discussions of concepts like the area and mass moments of inertia, Mohr’s circles, and the vector cross and triple scalar prod- ucts. The notation, as far as possible, will be a matrix notation that is easily entered into exist- ing symbolic computational programs like Maple, Mathematica, Matlab, and Mathcad. The desire to represent the components of three-dimensional fourth-order tensors that appear in anisotropic elasticity as the components of six-dimensional second-order tensors and thus rep- resent these components in matrices of tensor components in six dimensions leads to the non- traditional part of this appendix. This is also one of the nontraditional aspects in the text of the book, but a minor one. This is described in §A.11, along with the rationale for this approach. A.2. DEFINITION OF SQUARE, COLUMN, AND ROW MATRICES An r-by-c matrix, M, is a rectangular array of numbers consisting of r rows and c columns: ¯MM..
    [Show full text]
  • Teresa Blackford V. Welborn Clinic
    IN THE Indiana Supreme Court Supreme Court Case No. 21S-CT-85 Teresa Blackford Appellant (Plaintiff below) –v– Welborn Clinic Appellee (Defendant below) Argued: April 22, 2021 | Decided: August 31, 2021 Appeal from the Vanderburgh Circuit Court No. 82C01-1804-CT-2434 The Honorable David D. Kiely, Judge On Petition to Transfer from the Indiana Court of Appeals No. 19A-CT-2054 Opinion by Justice Goff Chief Justice Rush and Justices David, Massa, and Slaughter concur. Goff, Justice. Statutory limitations of action are “fundamental to a well-ordered judicial system.” See Bd. of Regents of Univ. of State of N. Y. v. Tomanio, 446 U.S. 478, 487 (1980). The process of discovery and trial, revealing ultimate facts that either help or harm the plaintiff, are “obviously more reliable if the witness or testimony in question is relatively fresh.” Id. And potential defendants, of course, seek to avoid indefinite liability for past conduct. C. Corman, 1 Limitation of Actions § 1.1, at 5 (1991). Naturally, then, “there comes a point at which the delay of a plaintiff in asserting a claim is sufficiently likely either to impair the accuracy of the fact-finding process or to upset settled expectations that a substantive claim will be barred” regardless of its merit. Tomanio, 446 U.S. at 487. At the same time, most courts recognize that certain circumstances may “justify an exception to these strong policies of repose,” extending the time in which a plaintiff may file a claim—a process known as “tolling.” Id. at 487–88. The circumstances here present us with these competing interests: the plaintiff, having been misinformed of a medical diagnosis by her provider, which dissolved its business more than five years prior to the plaintiff filing her complaint, seeks relief for her injuries on grounds of fraudulent concealment, despite expiration of the applicable limitation period.
    [Show full text]
  • Chapter 3 Motion in Two and Three Dimensions
    Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a.
    [Show full text]