A Normative Sugarcane Supply Function and Optimum
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Sugar, Steam and Steel: the Industrial Project in Colonial Java, 1830-1850
Welcome to the electronic edition of Sugar, Steam and Steel: The Industrial Project in Colonial Java, 1830-1885. The book opens with the bookmark panel and you will see the contents page. Click on this anytime to return to the contents. You can also add your own bookmarks. Each chapter heading in the contents table is clickable and will take you direct to the chapter. Return using the contents link in the bookmarks. The whole document is fully searchable. Enjoy. G Roger Knight Born in deeply rural Shropshire (UK), G Roger Knight has been living and teaching in Adelaide since the late 1960s. He gained his PhD from London University's School of Oriental and African Studies, where his mentors included John Bastin and CD Cowan. He is an internationally recognised authority on the sugar industry of colonial Indonesia, with many publications to his name. Among the latest is Commodities and Colonialism: The Story of Big Sugar in Indonesia, 1880-1940, published by Brill in Leiden and Boston in 2013. He is currently working on a 'business biography' — based on scores of his newly discovered letters back home — of Gillian Maclaine, a young Scot who was active as a planter and merchant in colonial Java during the 1820s and 1830s. For a change, it has almost nothing to do with sugar. The high-quality paperback edition of this book is available for purchase online: https://shop.adelaide.edu.au/ Sugar, Steam and Steel: The Industrial Project in Colonial Java, 1830-18 by G Roger Knight School of History and Politics The University of Adelaide Published in Adelaide by University of Adelaide Press The University of Adelaide Level 14, 115 Grenfell Street South Australia 5005 [email protected] www.adelaide.edu.au/press The University of Adelaide Press publishes externally refereed scholarly books by staff of the University of Adelaide. -

Perancangan Bangunan Tempat Pemrosesan Akhir Sampah Berdasarkan Peraturan Menteri Pekerjaan Umum Republik Indonesia Di Desa Samp
PERANCANGAN BANGUNAN TEMPAT PEMROSESAN AKHIR SAMPAH BERDASARKAN PERATURAN MENTERI PEKERJAAN UMUM REPUBLIK INDONESIA DI DESA SAMPIH, KECAMATAN WONOPRINGGO, KABUPATEN PEKALONGAN, PROVINSI JAWA TENGAH Oleh : Maria Della Strada D. O 114.130.149 INTISARI TPA Bojonglarang yang berada di Desa Linggoasri, Kecamatan Kajen, Kabupaten Pekalongan merupakan suatu TPA yang secara fisik sudah tidak layak lagi untuk digunakan dan harus segera dipindahkan. Berdasarkan hasil keputusan Badan Lingkungan Hidup (BLH) kabupaten Pekalongan rencana pembangunan TPA Sampah modern akan dilaksanakan di Desa Sampih, Kecamatan Wonopringgo, Kabupaten Pekalongan. Penelitian ini bertujuan untuk mengetahui kelayakan lahan yang akan dijadikan sebagai TPA tersebut dan melakukan perancangan TPA berdasarkan kondisi di lapangan. Metode yang digunakan dalam penelitian ini adalah metode pemetaan, survei, pengukuran, pengambilan sampel, pengukuran permeabilitas, penilaian, dan pembobotan sesuai SNI 03-3241-1994. Parameter yang dinilai untuk mengetahui kelayakan lahan TPA sampah adalah kriteria regional (kemiringan lereng, kondisi geologi, jarak terhadap sumber air minum, kedalaman muka air dan kawasan hutan lindung) dan kriteria penyisih (permeabilitas tanah, sistem aliran air tanah, bahaya banjir, pertanian, biologis, jalan menuju lokasi, transportasi sampah, jalan masuk, lalu lintas, kebisingan dan bau, curah hujan, tanah penutup, demografi dan estetika). Hasil yang telah dicapai dalam penelitian ini bahwa lokasi TPA di Desa Sampih masuk tingkat II (tidak layak) untuk kriteria regional dan perlu adanya masukan teknologi sehingga bisa dilanjutkan untuk tingkat kriteria penyisih. Tingkat kriteria penyisih lokasi ini termasuk tingkat II (sesuai). Perancangan TPA ini dilakukan di lahan seluas 20 Ha. Luas masing-masing zona antara lain; zona 1 dan zona 2 masing-masing seluas 3 Ha sedangkan zona 3, 4, 5 dan 6 masing – masing seluas 2 Ha. -

Sugar, Steam and Steel: the Industrial Project in Colonial Java, 1830-1885
Welcome to the electronic edition of Sugar, Steam and Steel: The Industrial Project in Colonial Java, 1830-1885. The book opens with the bookmark panel and you will see the contents page. Click on this anytime to return to the contents. You can also add your own bookmarks. Each chapter heading in the contents table is clickable and will take you direct to the chapter. Return using the contents link in the bookmarks. The whole document is fully searchable. Enjoy. G Roger Knight Born in deeply rural Shropshire (UK), G Roger Knight has been living and teaching in Adelaide since the late 1960s. He gained his PhD from London University's School of Oriental and African Studies, where his mentors included John Bastin and CD Cowan. He is an internationally recognised authority on the sugar industry of colonial Indonesia, with many publications to his name. Among the latest is Commodities and Colonialism: The Story of Big Sugar in Indonesia, 1880-1940, published by Brill in Leiden and Boston in 2013. He is currently working on a 'business biography' — based on scores of his newly discovered letters back home — of Gillian Maclaine, a young Scot who was active as a planter and merchant in colonial Java during the 1820s and 1830s. For a change, it has almost nothing to do with sugar. The high-quality paperback edition of this book is available for purchase online: https://shop.adelaide.edu.au/ Sugar, Steam and Steel: The Industrial Project in Colonial Java, 1830-18 Published in Adelaide by University of Adelaide Press The University of Adelaide Level 14, 115 Grenfell Street South Australia 5005 [email protected] www.adelaide.edu.au/press The University of Adelaide Press publishes externally refereed scholarly books by staff of the University of Adelaide. -

Kepala Bps Kabupaten Pekalongan Chief of Statistics of Pekalongan Regency
http://pekalongankab.bps.go.id 1 / 344 http://pekalongankab.bps.go.id 2 / 344 3 / 344 http://pekalongankab.bps.go.id KABUPATEN PEKALONGAN DALAM ANGKA 2017 Pekalongan Regency in Figures 2017 Nomor Katalog/Catalog Number : 1102001.3326 Nomor Publikasi/Publication Number : 33260.1602 Ukuran Buku/Book Size : 15 cm x 21 cm Jumlah Halaman/Total Pages : 354 Halaman Naskah/Manuscript : Badan Pusat Statistik Kabupaten Pekalongan BPS-Statistics of Pekalongan Regency Penyunting/Editor : Badan Pusat Statistik Kabupaten Pekalongan BPS-Statistics of Pekalongan Regency Gambar Kulit/Cover Design : Badan Pusat Statistik Kabupaten Pekalongan BPS-Statistics of Pekalongan Regency Diterbitkan oleh/Published by : Badan Pusat Statistik Kabupaten Pekalongan BPS-Statistics of Pekalongan Regency 4 / 344 http://pekalongankab.bps.go.id Boleh dikutip dengan menyebutkan sumbernya May be cited with reference to the source 5 / 344 http://pekalongankab.bps.go.id 6 / 344 http://pekalongankab.bps.go.id 7 / 344 http://pekalongankab.bps.go.id 8 / 344 http://pekalongankab.bps.go.id LAMBANG DAERAH KABUPATEN PEKALONGAN Lambang Daerah Kabupaten Pekalongan yang berupa perisai bersayap dalam ukuran bujur sangkar dengan perbandingan panjang dan lebar 1 : 1 ini, didasarkan pada SK DPRGR Kabupaten Pekalongan No. 4/PD/DPRGR Kabupaten Pekalongan No. 17/PD/DPRGR/11/71 tanggal 16 Pebruari 1971 tentang Penggunaan Lambang Daerah. Makna dan Isi Lambang A. Bintang, melambangkan Ketuhanan Yang Maha Esa mencerminkan bahwa warga penduduk Kabupaten Pekalongan umumnya menyakini dan berbhakti kepada Tuhan Yang Maha Esa. B. Sudut Lima pada Bintang, melambangkan Pancasila, Masyarakat di Kabupaten Pekalongan menyakini bahwa Pancasila merupakan sumber segala sumber hukum dalam mengurus, mengatur dan membina daerah. C. -

User's Guide for the Indonesia Family Life Survey, Wave 4
User's Guide for the Indonesia Family Life Survey, Wave 4 AND ANNA MARIE WATTIE We recommend the following citations for the IFLS data: For papers using IFLS1 (1993): Frankenberg, E. and L. Karoly. "The 1993 Indonesian Family Life Survey: Overview and Field Report." November, 1995. RAND. DRU-1195/1-NICHD/AID For papers using IFLS2 (1997): Frankenberg, E. and D. Thomas. ―The Indonesia Family Life Survey (IFLS): Study Design and Results from Waves 1 and 2‖. March, 2000. DRU-2238/1-NIA/NICHD. For papers using IFLS3 (2000): Strauss, J., K. Beegle, B. Sikoki, A. Dwiyanto, Y. Herawati and F. Witoelar. ―The Third Wave of the Indonesia Family Life Survey (IFLS3): Overview and Field Report‖. March 2004. WR-144/1- NIA/NICHD. For papers using IFLS4 (2007): Strauss, J., F. Witoelar, B. Sikoki and AM Wattie. ―The Fourth Wave of the Indonesia Family Life Survey (IFLS4): Overview and Field Report‖. March 2009. WR-675/1-NIA/NICHD. ii Preface This document describes some issues related to use of the fourth wave of the Indonesia Family Life Survey (IFLS4), alone and together with earlier waves of IFLS: IFLS1, 2 and 3. It is the second of six volumes documenting IFLS4. The first volume describes the basic survey design and implementation. The Indonesia Family Life Survey is a continuing longitudinal socioeconomic and health survey. It is based on a sample of households representing about 83% of the Indonesian population living in 13 of the nation’s 26 provinces in 1993. The survey collects data on individual respondents, their families, their households, the communities in which they live, and the health and education facilities they use. -

Jurnal Geografi Volume 13 No 2 (179 Dari 224)
Jurnal Geografi Volume 13 No 2 (179 dari 224) Jurnal Geografi Media Infromasi Pengembangan Ilmu dan Profesi Kegeografian RISIKO BENCANA DI KABUPATEN PEKALONGAN (DISASTER RISK IN PEKALONGAN REGENCY) Ananto Aji1, Wahid Akhsin Budi Nur Sidiq1, Satya Budi Nugraha1, Dewi Liesnoor Setyowati1, Nana Kariada Tri Martuti2 Lecturer of Geography Department of the Faculty of Social Sciences, UNNES1 and Lecturer of Biology of the Faculty of Mathematics and Sciences, UNNES2 Email: [email protected] Sejarah Artikel Diterima: Maret 2016 Disetujui: April 2016 Dipublikasikan: Juli 2016 Abstract Pekalongan Regency of Central Java is a region with high risk of disaster. Various kinds of disaster such as landslide, flood, drought, and tidal flood have somehow become “seasonal customer” for occurring in Pekalongan Regency. This research aimed to prepare the mapping of disaster risk in order to strengthen the efforts in reducing disaster risk in Pekalongan Regency. The research method applied in this research refers to the Head’s Regulation of National Risk Management Agency Number 2/2012. Since the risks of tidal flood were not yet included in the regulation, the field observation approach was used in this research. The analysis of disaster risk also considered the collecting method of disaster history by organizing focus group discussion (FGD) with the related parties. The research result showed that there were high risks of flood disaster covered some sub-districts such as Kajen, Kesesi, Wonopringgo, Karangdadap, Tirto, Wiradesa and Wonokerto; there were twenty six villages in total. High risk of landslide potentially occurred in large part of villages on the south area of Pekalongan Regency. High risk of drought was relatively evenly spread in the center area. -

Public Participation in Branding Road Corridor As Shopping Window Or Batik Industry at Pekalongan
Available online at www.sciencedirect.com ScienceDirect Procedia - Social and Behavioral Sciences 168 ( 2015 ) 76 – 86 AicE-Bs2014Berlin (formerly AicE-Bs2014Magdeburg) Asia Pacific International Conference on Environment-Behaviour Studies Sirius Business Park Berlin-yard field, Berlin, 24-26 February 2014 “Public Participation: Shaping a sustainable future” Public Participation in Branding Road Corridor as Shopping Window or Batik Industry at Pekalongan R. Siti Rukayah*a, Ardiyan Adhi Wibowob, Sri Hartuti Wahyuningruma aArchitecture Department, Engineering Faculty, Diponegoro University bArchitecture Department,Qur’anic Science University, Wonosobo, Central Java, Indonesia Abstract There are many cities in Indonesia that can be categorized as batik-industrial cities. Postal road that connects cities along the northern coast of Java Island passes right through Pekalongan. Through historical and naturalistic approach, this road is the promotional media for local citizens to display their industrial products, making it a shopping window. The image of Pekalongan as an industrial city is obtained naturally from the participation of its people. Pekalongan is a globally professional city that has sustained its image since 1800s. The continuation of the research is to compare Pekalongan to another city that has successfully implemented the concept and become an advanced industrial city. © 2015 Published by Elsevier Ltd. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/3.0/© 2014 Published by Elsevier Ltd. Selection). and peer-review under responsibility of the Centre for Environment- PeerBehaviour-review under Studies responsibility (cE-Bs), ofFaculty Centre forof Architecture,Environment-Behaviour Planning Studies & Surv (cE-Bs),eying, Faculty UniversitiTeknologi of Architecture, Planning MARA, & Malaysia.Surveying, Universiti Teknologi MARA, Malaysia. -

List Agen 201610.Xlsx
REGION KABUPATEN KECAMATAN KELURAHAN ALAMAT AGEN AGEN ID NAMA AGEN PIC AGEN JARINGAN KANTOR CENTRAL JAVA BANTUL BAMBANGLIPURO MULYODADI PAKER RT 004 213ED0107P000058 MAYLA CELL MARYADI BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO MULYODADI GAYAMAN KRATON RT 006 213ED0107P000026 MINIMIZE TRI MINTARJO BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SIDOMULYO NGAMPELAN 213ED0107P000049 HT CELL SUTRININGSIH BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SIDOMULYO JL. PAKER DAWETAN SIDOMULYO 213ED0106P000054 SUN STAR SUNU BADI BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SIDOMULYO KARANGASEM DK VIII SELO RT 004 SIDOMULYO 213ED0107P000059 KIOS TANI MUDA RIZKY CAHYA PRATAMA BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SIDOMULYO JALAN PARANGTRITIS SIDOMULYO 213ED0107P000022 FITRIA CELL HUSEIN ALKAF BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SIDOMULYO TURI RT 004 213ED0107P000031 MOSA CELL TIWUK NURSANTI BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SUMBERMULYO GANJURAN INDAH NO 25 RT 08 213ED0107P000018 LOJI CELL AGUS SANTOSO BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIPURO SUMBERMULYO DERMAN GERSIK RT 006 213ED0107P000052 PASAR PULSA SRI UTAMI BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIUPURO SIDOMULYO CUNGKUP RT1 213ED0106P000004 TOKO BU ETI ETI SUSANTI BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BAMBANGLIUPURO SIDOMULYO JL. SAMAS KM18 213ED0106P000007 WHYAND CELL WINI SUNARNININGSIH BTPN PURNABAKTI BANTUL CENTRAL JAVA BANTUL BANGUNTAPAN BANGUNTAPAN -

Download (4MB)
PENGARUH PELAYANAN, REPUTASI DAN PROSEDUR TERHADAP MINAT NASABAH DALAM PENGAJUAN PEMBIAYAAN MURABAHAH PADA LEMBAGA KEUANGAN SYARIAH (Studi Kasus KSPPS BTM Pekalongan Cabang Wonopringgo Kabupaten Pekalongan) SKRIPSI Diajukan Untuk Memenuhi Sebagaian Syarat Memperoleh Gelar Sarjana Ekonomi Syariah (S.E) Oleh: LIZA TRI SEPTIANI NIM. 2013114220 JURUSAN EKONOMI SYARIAH FAKULTAS EKONOMI DAN BISNIS ISLAM INSTITUT AGAMA ISLAM NEGERI PEKALONGAN 2018 Perpustakaan IAIN Pekalongan PENGARUH PELAYANAN, REPUTASI DAN PROSEDUR TERHADAP MINAT NASABAH DALAM PENGAJUAN PEMBIAYAAN MURABAHAH PADA LEMBAGA KEUANGAN SYARIAH (Studi Kasus KSPPS BTM Pekalongan Cabang Wonopringgo Kabupaten Pekalongan) SKRIPSI Diajukan Untuk Memenuhi Sebagaian Syarat Memperoleh Gelar Sarjana Ekonomi Syariah (S.E) Oleh: LIZA TRI SEPTIANI NIM. 2013114220 JURUSAN EKONOMI SYARIAH FAKULTAS EKONOMI DAN BISNIS ISLAM INSTITUT AGAMA ISLAM NEGERI PEKALONGAN 2018 Perpustakaan IAIN Pekalongan i PENGARUH PELAYANAN, REPUTASI DAN PROSEDUR TERHADAP MINAT NASABAH DALAM PENGAJUAN PEMBIAYAAN MURABAHAH PADA LEMBAGA KEUANGAN SYARIAH (Studi Kasus KSPPS BTM Pekalongan Cabang Wonopringgo Kabupaten Pekalongan) SKRIPSI Diajukan Untuk Memenuhi Sebagaian Syarat Memperoleh Gelar Sarjana Ekonomi Syariah (S.E) Oleh: LIZA TRI SEPTIANI NIM. 2013114220 JURUSAN EKONOMI SYARIAH FAKULTAS EKONOMI DAN BISNIS ISLAM INSTITUT AGAMA ISLAM NEGERI PEKALONGAN 2018 Perpustakaan IAIN Pekalongan i i Perpustakaan IAIN Pekalongan Perpustakaan IAIN Pekalongan Perpustakaan IAIN Pekalongan PEDOMAN TRANSLITERASI ARAB-LATIN Pedoman transliterasi yang digunakan dalam penulisan skripsi ini adalah hasil Putusan Bersama Menteri Agama Republik Indonesia No. 158 tahun 1987 dan Menteri Pendidikan dan Kebudayaan Republik Indonesia No. 0543b/U/1987. Transliterasi tersebut digunakan untuk menulis kata-kata Arab yang dipandang belum diserap ke dalam bahasa Indonesia. Kata-kata Arab yang sudah diserap ke dalam bahasa Indonesia sebagaimana terlihat dalam Kamus Linguistik atau Kamus Besar Bahasa Indonesia (KBBI). -

Hubungan Mekanisme Koping Dengan Tingkat Hipertensi Di Wilayah Kerja Puskesmas Wonopringgo Kabupaten
HUBUNGAN MEKANISME KOPING DENGAN TINGKAT HIPERTENSI DI WILAYAH KERJA PUSKESMAS WONOPRINGGO KABUPATEN PEKALONGAN THE CORRELATION OF COPING MECHANISM WITH HYPERTENSION LEVEL OF HYPERTENSIVE PATIENTS AT THE WORKING AREA PUBLIC HEALTH CENTER OF WONOPRINGGO, PEKALONGAN REGENCY Afif Eka Adhietya Program Studi Sarjana Keperawatan Universitas Muhammadiyah Pekajangan Pekalongan Rita Dwi Hartanti Staf Pengajar Program Studi Sarjana Keperawatan Universitas Muhammadiyah Pekajangan Pekalongan ABSTRAK Kasus hipertensi menurut para pakar penyebab utamanya adalah stres. Penanganan stres perlu mekanisme koping agar tidak terjadi dampak yang lebih buruk lagi. Semakin adaptif mekanisme koping seseorang maka semakin ringan tingkat stres yang dimilikinya, begitu juga sebaliknya. Penelitian ini bertujuan untuk mengetahui hubungan mekanisme koping dengan tingkat hipertensi pasien hipertensi. Desain penelitian deskriptif korelatif melalui pendekatan cross sectional. Teknik pengambilan sampel dalam penelitian ini adalah cluster sampling dengan jumlah 71 responden. Alat pengumpulan data menggunakan kuesioner. Uji statistik menggunakan uji Kolmogorov-Smirnov. Hasil penelitian didapatkan lebih dari separuh (52,1%) responden memiliki mekanisme koping adaptif, hampir separuh (49,3%) responden memiliki tingkat hipertensi dalam kategori hipertensi ringan. Hasil uji statistik didapatkan ρ value sebesar 0,001 (<0,05) menunjukkan ada hubungan yang signifikan mekanisme koping dengan tingkat hipertensi pasien hipertensi di wilayah kerja Puskesmas Wonopringgo Kabupaten Pekalongan. Hasil penelitian ini merekomendasikan tenaga kesehatan dalam menangani pasien hipertensi perlu mengarahkan mekanisme koping pasien yang adaptif guna mengurangi stres sehingga menurunkan tekanan darah. Kata kunci : mekanisme koping, tingkat hipertensi ABSTRACT The case of hypertension according to experts the main cause is stress. Handling stress needs a coping mechanism so that no worse impact occurs. The more adaptive a person's coping mechanism, the lighter the level of stress it has, and vice versa. -

East Java Traditional Batik Marketing Model for the Development of Management Information System As Efforts to Preserve the Nation's Cultural
International Journal of Business and Management Invention ISSN (Online): 2319 – 8028, ISSN (Print): 2319 – 801X www.ijbmi.org || Volume 5 Issue 11 || November. 2016 || PP—01-16 East Java Traditional Batik Marketing Model for the Development of Management Information System as Efforts to Preserve the Nation's Cultural Januar Wibowo1, Haryanto Tanuwijaya1, Achmad Yanu Alif Fianto1. 1(Management Program – Institut Bisnis dan Informatika Stikom Surabaya) ABSTRACT: Batik is one of Indonesian cultural heritage, which has been transformed as a legacy honored and admired by the world. Batik is not just a tool to decorate themselves, but batik is a cultural symbol that is closely related to the philosophy of the motif is concerned. East Java can be considered as having diversity motif that has a high historical value. These advantages in addition to foster pride as a civilized nation, but the risk may be claimed as the cultural heritage of other countries in the world. Therefore, the ultimate goal of this research is to plan, design and produce a management information system application of traditional batik East Java which uses multiplatform capabilities with the use of appropriate technology. These applications are planned, designed and produced from their grand strategy that is arrayed in models of marketing management to popularize various kinds of traditional batik in East Java, which is not only of patterns and motifs, but also includes elements of the philosophy contained in batik. Keywords: Batik, East Java, Marketing Model, Management Information System I. INTRODUCTION Batik is one of Indonesian cultural heritage, which has been transformed into a culture that revered and admired by the world. -
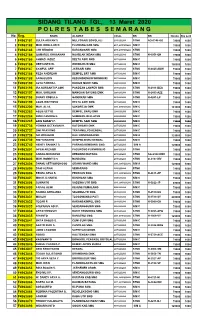
SIDANG TILANG TGL, 13 Maret 2020 P O L R E S T a B E S S E M a R a N G No
SIDANG TILANG TGL, 13 Maret 2020 P O L R E S T A B E S S E M A R A N G No. Reg. NAMA ALAMAT PASAL BB BB Denda Bia perk 1 F4963181 ZULFA ARIYANTI MULYOSARI BOYOLALI 291 UULAJ STNK AD-6745-GD 79000 1000 2 F4963182 MUH. KHOLILUR R. PLUWANG KAB.SMG 287, 288 UULAJ SIM C 79000 1000 3 F4963183 JAN WIDODO KARANGSARI SMG 281, 291 UULAJ STNK 79000 1000 4 F4963184 QOMARUL KHASANAH NGABLAK INDAH SMG 281 UULAJ STNK H-6051-QH 79000 1000 5 F4963185 AHMAD JAZUZ DELTA ASRI SMG 287 UULAJ SIM C 79000 1000 6 F4963186 HERYANTO W. WIDOHARJO SMG 287 UULAJ SIM C 100000 1000 7 F4963187 SYAIFUL AFIF JATISARI SMG 287 UULAJ STNK H-4425-ADW 79000 1000 8 F4963188 REZA ANDREAN DEMPEL BRT SMG 287 UULAJ SIM C 79000 1000 9 F4963189 SAWALUDIN KEDUNGRINGIN WONOGIRI 287 UULAJ SIM C 79000 1000 10 F4963190 ALYA FARIHA I. KUKILO MUKTI SMG 288 UULAJ SIM C 79000 1000 11 F4963196 IRA NURSANTI P.AMK PANDEAN LAMPER SMG 281 UULAJ STNK H-2101-BEG 79000 1000 12 F4963197 MUH. SHOLIKIN MANGIAN SAYUNG DMK 288 UULAJ STNK H-2495-AZE 79000 1000 13 F4963198 DHANY ROBI A.S GANDIKAN SMG 281 UULAJ STNK H-4261-LP 79000 1000 14 F4963199 AGUS WAHYONO DELTA ASRI SMG 287 UULAJ SIM C 79000 1000 15 F4963200 MUH. ALI A. SUKOREJO DMK 285, 280 UULAJ SIM C 161000 1000 16 F4963282 AGUS SETYO DEMPEL BARU DMK 288 UULAJ SIM C 79000 1000 17 F4963284 RIZKI CANDRA K.