Superheavy Elements*
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
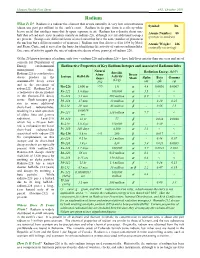
Radium What Is It? Radium Is a Radioactive Element That Occurs Naturally in Very Low Concentrations Symbol: Ra (About One Part Per Trillion) in the Earth’S Crust
Human Health Fact Sheet ANL, October 2001 Radium What Is It? Radium is a radioactive element that occurs naturally in very low concentrations Symbol: Ra (about one part per trillion) in the earth’s crust. Radium in its pure form is a silvery-white heavy metal that oxidizes immediately upon exposure to air. Radium has a density about one- Atomic Number: 88 half that of lead and exists in nature mainly as radium-226, although several additional isotopes (protons in nucleus) are present. (Isotopes are different forms of an element that have the same number of protons in the nucleus but a different number of neutrons.) Radium was first discovered in 1898 by Marie Atomic Weight: 226 and Pierre Curie, and it served as the basis for identifying the activity of various radionuclides. (naturally occurring) One curie of activity equals the rate of radioactive decay of one gram (g) of radium-226. Of the 25 known isotopes of radium, only two – radium-226 and radium-228 – have half-lives greater than one year and are of concern for Department of Energy environmental Radioactive Properties of Key Radium Isotopes and Associated Radionuclides management sites. Natural Specific Radiation Energy (MeV) Radium-226 is a radioactive Abun- Decay Isotope Half-Life Activity decay product in the dance Mode Alpha Beta Gamma (Ci/g) uranium-238 decay series (%) (α) (β) (γ) and is the precursor of Ra-226 1,600 yr >99 1.0 α 4.8 0.0036 0.0067 radon-222. Radium-228 is a radioactive decay product Rn-222 3.8 days 160,000 α 5.5 < < in the thorium-232 decay Po-218 3.1 min 290 million α 6.0 < < series. -

Song Artist Or Soundtrack Language Tightrope Janelle Monae English
Song Artist or Soundtrack Language Tightrope Janelle Monae English Come Alive [War of the Roses] Janelle Monae English Why this kolaveri di Dhanush Urdu Ghoom tana Janoon Urdu Count your blessings Nas & Damian Jr English America K'naan Somali/ English Mahli Souad Massi Arabic (Tunisian) Helwa ya baladi Dalida Arabic (Egyptian) Stop for a Minute K'naan English Miracle Worker SuperHeavy English Crazy Gnarls Barkley English 1977 Ana Tijoux Spanish (Chilean) Nos Hala Asalah Arabic Don't Let Me Be Misunderstood Santa Esmeralda / Kill Bill Vol. 1 Original Soundtrack Never Can Say Goodbye Jackson Five English My Doorbell The White Stripes English Peepli Live Various Artists, Indian Ocean Hindi or Urdu Forget You Camilla and the Chickens, The Muppets Soundtrack Chicken?? Ring of Fire Johnny Cash English I Was Born on the Day Before Yesterday The Wiz English Y'All Got It The Wiz English Everything Michael Buble English I'm Yours Jason Mraz English Something's Gotta Hold on Me Etta James English Somebody to Love Queen English Al Bosta Fairouz Arabic (Lebanese) Kifak Inta Fairouz Arabic (Lebanese) Etfarag ala najsak Asala Nasri Arabic (Egyptian) Make it bun dem Skrillex, Damian English Statesboro Blues Taj Mahal English Albaniz: Zambra-Capricho, Cordoba, Zor David Russell Spanish classical Volver Estrella Morente from Volver: Musica de la Pelicula Spanish Solo le pido a Dios Leon Gieco Spanish Mambo Italiano Rosemary Clooney English / Italian Botch-A-Me (Baciani Piccina) Rosemary Clooney English / Italian Satyameva Jayathe SuperHeavy English / ? -

The Use of Cosmic-Rays in Detecting Illicit Nuclear Materials
The use of Cosmic-Rays in Detecting Illicit Nuclear Materials Timothy Benjamin Blackwell Department of Physics and Astronomy University of Sheffield This dissertation is submitted for the degree of Doctor of Philosophy 05/05/2015 Declaration I hereby declare that except where specific reference is made to the work of others, the contents of this dissertation are original and have not been submitted in whole or in part for consideration for any other degree or qualification in this, or any other Univer- sity. This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration, except where specifically indicated in the text. Timothy Benjamin Blackwell 05/05/2015 Acknowledgements This thesis could not have been completed without the tremendous support of many people. Firstly I would like to express special appreciation and thanks to my academic supervisor, Dr Vitaly A. Kudryavtsev for his expertise, understanding and encourage- ment. I have enjoyed our many discussions concerning my research topic throughout the PhD journey. I would also like to thank my viva examiners, Professor Lee Thomp- son and Dr Chris Steer, for the time you have taken out of your schedules, so that I may take this next step in my career. Thanks must also be given to Professor Francis Liven, Professor Neil Hyatt and the rest of the Nuclear FiRST DTC team, for the initial oppor- tunity to pursue postgraduate research. Appreciation is also given to the University of Sheffield, the HEP group and EPRSC for providing me with the facilities and funding, during this work. -

Yearly Academic Journal Issn
Peer-Reviewed YEARLY ACADEMIC JOURNAL 2020-21 Volume: XX ISSN : 2348-9014 Kalindi College (University of Delhi) NAAC Accredited ‘A’ Grade College East Patel Nagar, New Delhi - 110008 Peer Reviewed YEARLY ACADEMIC JOURNAL Kalindi College Volume: XX 2020-21 ISSN: 2348-9014 (UNIVERSITY OF DELHI) East Patel Nagar, New Delhi – 110008 English Section: Editor: Dr. Anjali Bansal Co-editor: Dr. Chaity Das Hindi Section: Editor: Dr. Nisha Goyal Co-editor: Dr. Raksha Geeta Editorial Board: Ms. Shipra Gupta Dr. Triranjita Srivastava Dr. Reena Jain Ms. Tanu Sharma Mr. Suresh Kumar Principal’s Message The Academic Journal of any college reflects the academic standard of that institution. The articles contained in the journal prove the credibility of the writers. In this time of pandemic where many of the publishing houses have deferred their issues of various journals, we at Kalindi decided to go ahead with its annual publication and release. The journal consists of articles from multi-disciplinary fields in three different languages. This shows the integration in diversity. Today, I am so happy to announce the release of the present issue of our annual journal. I wish to congratulate all the writers of various academic disciplines for their valuable contributions. I am also grateful to the Editorial team who have worked so hard to bring out this issue. I wish all the best to the team and great success ahead. Dr. Naina Hasija Principal Editorial Nearly two decades ago, then principal, Dr. Malti, with an academic bent of mind conceived the idea of giving life to the academic activities of the intellectual minds of national and international fame and this Academic Journal was the first manifestation of the same. -

Two-Proton Radioactivity 2
Two-proton radioactivity Bertram Blank ‡ and Marek P loszajczak † ‡ Centre d’Etudes Nucl´eaires de Bordeaux-Gradignan - Universit´eBordeaux I - CNRS/IN2P3, Chemin du Solarium, B.P. 120, 33175 Gradignan Cedex, France † Grand Acc´el´erateur National d’Ions Lourds (GANIL), CEA/DSM-CNRS/IN2P3, BP 55027, 14076 Caen Cedex 05, France Abstract. In the first part of this review, experimental results which lead to the discovery of two-proton radioactivity are examined. Beyond two-proton emission from nuclear ground states, we also discuss experimental studies of two-proton emission from excited states populated either by nuclear β decay or by inelastic reactions. In the second part, we review the modern theory of two-proton radioactivity. An outlook to future experimental studies and theoretical developments will conclude this review. PACS numbers: 23.50.+z, 21.10.Tg, 21.60.-n, 24.10.-i Submitted to: Rep. Prog. Phys. Version: 17 December 2013 arXiv:0709.3797v2 [nucl-ex] 23 Apr 2008 Two-proton radioactivity 2 1. Introduction Atomic nuclei are made of two distinct particles, the protons and the neutrons. These nucleons constitute more than 99.95% of the mass of an atom. In order to form a stable atomic nucleus, a subtle equilibrium between the number of protons and neutrons has to be respected. This condition is fulfilled for 259 different combinations of protons and neutrons. These nuclei can be found on Earth. In addition, 26 nuclei form a quasi stable configuration, i.e. they decay with a half-life comparable or longer than the age of the Earth and are therefore still present on Earth. -

68 Th ACCELERATOR USERS WORKSHOP JULY 05, 2020 (SUNDAY) 09:00 – 09:15 WELCOME ADDRESS by DIRECTOR, IUAC FOLLOWED by REMARKS by CHAIRMAN, AUC
TENTATIVE PRESENTATION SCHEDULE 68 th ACCELERATOR USERS WORKSHOP JULY 05, 2020 (SUNDAY) 09:00 ± 09:15 WELCOME ADDRESS BY DIRECTOR, IUAC FOLLOWED BY REMARKS BY CHAIRMAN, AUC Session Chairperson: 09:15 ± 11:00 Session I: BTR- 1, 3, 5 (10+2 Minutes)/ BTR- 5 & 1, 2, 3 (15+3 Minutes)/ BTR- 2 (12+3 Minutes) 68139 10Be and 26Al cosmogenic radionuclides application to estimate the erosion rate of Aravalli mountain range: Impact (10+2) on Landscape evolution.: Dr. Madhav Krishna Murari, Inter University Accelerator Center, New Delhi. Min. 68140 36Cl measurement using Accelerator Mass Spectrometry (AMS).: Dr. Pavitra, Inter University Accelerator Center, (10+2) New Delhi. Min. 68107 10Be and 26Al measurement work: Mr. Bilal Ahmad Sonu, C/o. Dr. Meenal Mishra, School Of Sciences, IGNOU, (10+2) New Delhi. Min. 68120 Examining long-term social and environmental histories at Tekkalakota, Ballari District, Karnataka.: Dr. Vinayak, (10+2) Indraprastha College for Women, University of Delhi, Civil Lines, Delhi. Min. 68329 Chronostratigraphic Reconstruction of Cultural Sequences of Early, Mature and Late Harappan Civilisation: Tigrana.: (10+2) Mr. Pawan Kumar, Faculty of Earth, Environment and Space Sciences, Bhiwani, Haryana. Min. 68208 Mapping glacial dynamics in the Jankar Chhu Watershed, Lahaul Himalaya.: Mr. Suresh Das, Ph.D. Research Scholar, (12+3) Jawaharlal Nehru University, New Delhi. Min. 68203 Reconstructing Glacial Phases and Palaeo-environment in a part of the Upper Beas Basin, Himachal Pradesh.: (12+3) Ms. Ishita Manna, Ph.D Scholar, Jawaharlal Nehru University, New Delhi. Min. 68213 Glacier dynamics and palaeo reconstruction in Milang Watershed, Lahaul Himalaya, Himachal Pradesh.: (12+3) Mr. -

Grammy® and Academy Award® Winner A.R. Rahman's The
For Immediate Release: October 6, 2017 GRAMMY® AND ACADEMY AWARD® WINNER A.R. RAHMAN’S THE FLYING LOTUS RELEASED TODAY ON KM MUSIQ RECORD LABEL Photo credit: Brandon Patoc and James Holt Conductor Ricardo Averbach led the Seattle Symphony, Seattle Symphony Chorale and Seattle Girls’ Choir Prime Voci ensemble in the world premiere of The Flying Lotus commissioned by the Seattle Symphony Seattle Symphony Assistant Concertmaster Simon James featured as soloist Worldwide Release: October 6, 2017 Seattle, WA – Grammy® and Academy Award®-winning composer A.R. Rahman releases a recording of the world premiere of The Flying Lotus on October 6, 2017. Commissioned by the Seattle Symphony and recorded live in concert, The Flying Lotus is Rahman’s first composition solely for orchestra and features Seattle Symphony’s Second Assistant Concertmaster Simon James as the violin soloist. “The Flying Lotus is a musical impression of where India was and where it’s going,” says Rahman in an interview with The Seattle Times. “India is very progressive now. People are in such a very strong kind of mood. I thought I should capture musically those feelings of elation and also helplessness in a way. How can you say that musically, and also with a sense of pride in it? It’s hard to explain in words, but I thought music could communicate those emotions.” The Flying Lotus was commissioned for the Seattle Symphony’s ninth annual Celebrate Asia concert, held on May 12, 2017. This cultural celebration is now a signature event in Seattle, presented in partnership with local Asian leaders from the region’s Chinese, Filipino, Indian, Indonesian, Japanese, Korean, Thai and Vietnamese communities. -

"Indoor Radon and Radon Decay Product Measurement Device Protocols"
"Indoor Radon and Radon Decay Product Measurement Device Protocols" U.S. Environmental Protection Agency Office of Air and Radiation (6604J) EPA 402-R-92-004, July 1992 (revised) Table of Contents Disclaimer Acknowledgements Significant Changes in This Revision Radon and Radon Decay Product Measurement Methods Section 1: General Considerations 1.1 Introduction and Background 1.2 General Guidance on Measurement Strategy, Measurement Conditions, Device Location Selection, and Documentation 1.3 Quality Assurance Section 2: Indoor Radon Measurement Device Protocols 2.1 Protocol for Using Continuous Radon Monitors (CR) to Measure Indoor Radon Concentrations 2.2 Protocol for Using Alpha Track Detectors (AT or ATD) to Measure Indoor Radon Concentrations 2.4 Protocol for Using Activated Charcoal Adsorption Devices (AC) to Measure Indoor Radon Concentrations 2.5 Protocol for Using Charcoal Liquid Scintillation (LS) Devices to Measure Indoor Radon Concentrations 2.6 Protocol for Using Grab Radon Sampling (GB, GC, GS), Pump/Collapsible Bag Devices (PB), and Three-Day Integrating Evacuated Scintillation Cells (SC) to Measure Indoor Radon Concentrations 2.7 Interim Protocol for Using Unfiltered Track Detectors (UT) to Measure Indoor Radon Concentrations Section 3: Indoor Radon Decay Product Measurement Device Protocols 3.1 Protocol for Using Continuous Working Level Monitors (CW) to Measure Indoor Radon Decay Product Concentrations 3.2 Protocol for Using Radon Progeny Integrating Sampling Units (RPISU or RP) to Measure Indoor Radon Decay Product Concentrations 3.3 Protocol for Using Grab Sampling-Working Level (GW) to Measure Indoor Radon Decay Product Concentrations Glossary References Please Note: EPA closed its National Radon Proficiency Program (RPP) in 1998. -

Energy What Is a Nuclear Reaction?
4/16/2016 Option C: Energy C.3 : Nuclear Fusion and Fission What is a nuclear reaction? • A nuclear reaction is any reaction that involves the nucleus. • These reactions change the identity of an atom, as opposed to chemical reactions which only involve valence electrons. 1 4/16/2016 The nucleus • The nucleus is made up of protons and neutrons. • We know what the protons do – they provide an electrostatic attraction to the electrons close… but what about the neutrons? The Neutrons • The major function of the neutrons is to hold the nucleus together. • The neutrons provide a strong nuclear force of attraction within the nucleus, counteracting the repulsion between the positively charged protons. 2 4/16/2016 How is the nucleus held together? • In the 1930’s it was first observed that the mass of an atoms nucleus is less than the sum of the masses of the protons + neutrons…? • Some of the mass of the nucleus is converted into energy to hold the nucleus together. 3 4/16/2016 Mass Defect • The difference in mass of the nucleus and it’s parts is referred to as the mass defect, and the energy (e=mc 2) it provided is called the nuclear binding energy. 4 4/16/2016 Nuclear vs. Chemical Reactions • This nuclear binding energy is released during nuclear reactions (fission & fusion), and is ~1,000,000X greater than the chemical bond energy released during chemical reactions. What makes an isotope radioactive? • Elements are radioactive when their nucleus is unstable. • The stabilizing force of the neutrons is effective for smaller elements, though all elements above lead are radioactive. -

Nuclear Data As the Alternative Information of Decay and Analyzer
Usman Kadir, NuCLEAR Data as The alternative Information of decay and Analyzer NuCLEAR Data as The Alternative Information of Decay and Analyzer Usman Kadir Pusat Pendidikan dan Pelatihan BA TAN Abstract NuCLEAR Data is the name of visual, color-coded computer program of "Chart of Nuclides" or "Segre Chart". The program gives you comprehensive nuclear decay data that include data on alpha, beta, gamma, x-ray decay etc., and comprehensive search by energy, intensity, half life, radiation type or name of nuclide. NuCLEAR Data is able to show visual decay product and couldfunction as Multi Nuclides Identification and Multi Elements Identification Analysis. It is constructed using Visual Basic Compiler. Abstak NuCLEAR Data adalah nama program komputer untuk peta nuklida atau Segre Chart; data tervisual dan dikodekan warna. Program ini memberikan anda data peluruhan nuklir secara komprehensif, yang meliputi peluruhan alpha, beta, gamma, sinar-x dan dapat mencari energi, intensitas, waktu paro, jenis radiasi dan nama nuklida. NuCLEAR Data dapat menampilkan produk peluruhan secara visual dan dapat berfungsi sebagai analisis untuk Identifikasi multi nuklida dan identifikasi unsur-unsur. Program ini dibuat dengan Visual Basic. Chart of the Nuclides The "Chart of the Nuclides" or Segre Chart is shown in a colored mode, including details Chart of the Nuclides is a plot of all known for each nuclide's meta-stable states. nuclides as a function of Z (Atomic number), in the y-axis, and N (number of neutrons), in NuCLEAR for Windows 95/98/2000IXP is a the x-axis. visual Nuclear Data Library. It can be used as a standalone information system. -

Binding Blocks: Building the Universe One Nucleus at the Time
Binding Blocks: building the Universe one nucleus at the time C. Aa. Diget, A. Pastore, K. Leech, T. Haylett , S. Lock, T. Sanders, M. Shelley, H. V. Willett, Department of Physics, University of York, Heslington, York, Y010 5DD, United Kingdom J. Keegans, E.A. Milne Centre for Astrophysics School of Mathematics and Physical Sciences, University of Hull, Hull, HU6 7RX, United Kingdom L. Sinclair, Castle Hill Hospital, Cottingham, HU16 5JQ, United Kingdom E. C. Simpson, Department of Nuclear Physics, Research School of Physics and Engineering, The Australian National University, Canberra ACT 2601, Australia and the Binding Blocks collaboration #JOEJOH #JOEJOH #JOEJOH #MPDLT #MPDLT #MPDLT #VJMEJOHUIF6OJWFSTF #VJMEJOHUIF6OJWFSTF #VJMEJOHUIF6OJWFSTF E-mail: [email protected] POFOVDMFVTBUBUJNF POFOVDMFVTBUBUJNF POFOVDMFVTBUBUJNF Abstract. We present a new teaching and outreach activity based around the construction of a three-dimensional chart of isotopes using LEGOr bricksz. The activity, Binding Blocks, demonstrates nuclear and astrophysical processes through a seven-meter chart of all nuclear isotopes, built from over 26,000 LEGOr bricks. It integrates A-level and GCSE curricula across areas of nuclear physics, astrophysics, arXiv:1610.02296v2 [physics.ed-ph] 18 Oct 2016 and chemistry, including: nuclear decays (through the colours in the chart); nuclear binding energy (through tower heights); production of chemical elements in the cosmos; fusion processes in stars and fusion energy on Earth; as well as links to medical physics, particularly diagnostics and radiotherapy. z LEGOr is a trademark of the LEGO Group of companies which does not sponsor, authorise or endorse the present work. Binding Blocks: building the Universe one nucleus at the time 2 1. -

IUPAC/IUPAP Provisional Report)
Pure Appl. Chem. 2018; 90(11): 1773–1832 Provisional Report Sigurd Hofmanna,*, Sergey N. Dmitrieva, Claes Fahlanderb, Jacklyn M. Gatesb, James B. Robertoa and Hideyuki Sakaib On the discovery of new elements (IUPAC/IUPAP Provisional Report) Provisional Report of the 2017 Joint Working Group of IUPAC and IUPAP https://doi.org/10.1515/pac-2018-0918 Received August 24, 2018; accepted September 24, 2018 Abstract: Almost thirty years ago the criteria that are currently used to verify claims for the discovery of a new element were set down by the comprehensive work of a Transfermium Working Group, TWG, jointly established by IUPAC and IUPAP. The recent completion of the naming of the 118 elements in the first seven periods of the Periodic Table of the Elements was considered as an opportunity for a review of these criteria in the light of the experimental and theoretical advances in the field. In late 2016 the Unions decided to estab- lish a new Joint Working Group, JWG, consisting of six members determined by the Unions. A first meeting of the JWG was in May 2017. One year later this report was finished. In a first part the works and conclusions of the TWG and the Joint Working Parties, JWP, deciding on the discovery of the now named elements are summarized. Possible experimental developments for production and identification of new elements beyond the presently known ones are estimated. Criteria and guidelines for establishing priority of discovery of these potential new elements are presented. Special emphasis is given to a description for the application of the criteria and the limits for their applicability.