DOCSLIB.ORG

Modern Physics to Which He Did This Observation, Usually to Within About 0.1%

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modern Physics to Which He Did This Observation, Usually to Within About 0.1% Chapter 12 NUCLEAR STRUCTURE AND RADIOACTIVITY Radioactive isotopes have proven to be valuable tools for medical diagnosis. The photo shows gamma-ray emission from a man who has been treated with a radioactive element. The radioactivity concentrates in locations where there are active cancer tumors, which show as bright areas in the gamma-ray scan. This patient’s cancer has spread from his prostate gland to several other locations in his body. 370 Chapter 12 | Nuclear Structure and Radioactivity The nucleus lies at the center of the atom, occupying only 10−15 of its volume but providing the electrical force that holds the atom together. Within the nucleus there are Z positive charges. To keep these charges from flying apart, the nuclear force must supply an attraction that overcomes their electrical repulsion. This nuclear force is the strongest of the known forces; it provides nuclear binding energies that are millions of times stronger than atomic binding energies. There are many similarities between atomic structure and nuclear structure, which will make our study of the properties of the nucleus somewhat easier. Nuclei are subject to the laws of quantum physics. They have ground and excited states and emit photons in transitions between the excited states. Just like atomic states, nuclear states can be labeled by their angular momentum. There are, however, two major differences between the study of atomic and nuclear properties. In atomic physics, the electrons experience the force provided by an external agent, the nucleus; in nuclear physics, there is no such external agent. In contrast to atomic physics, in which we can often consider the interactions among the electrons as a perturbation to the primary interaction between electrons and nucleus, in nuclear physics the mutual interaction of the nuclear constituents is just what provides the nuclear force, so we cannot treat this complicated many- body problem as a correction to a single-body problem. We therefore cannot avoid the mathematical difficulties in the nuclear case, as we did in the atomic case. The second difference between atomic and nuclear physics is that we cannot write the nuclear force in a simple form like the Coulomb force. There is no closed-form analytical expression that can be written to describe the mutual forces of the nuclear constituents. In spite of these difficulties, we can learn a great deal about the properties of the nucleus by studying the interactions between different nuclei, the radioactive decay of nuclei, and the properties of some nuclear constituents. In this chapter and the next we describe these studies and how we learn about the nucleus from them. 12.1 NUCLEAR CONSTITUENTS The work of Rutherford, Bohr, and their contemporaries in the years between 1911 and 1920 showed that the positive charge of the atom is confined in a very small nuclear region at the center of the atom, that the nucleus in an atom of atomic number Z has a charge of +Ze, and that the nucleus provides most (99.9%) Enrico Fermi (1901–1954, Italy- of the atomic mass. It was also known that the masses of the atoms (measured in United States). There is hardly a field atomic mass units) were very nearly integers; a glance at Appendix D confirms of modern physics to which he did this observation, usually to within about 0.1%. We call this integer A the mass not make contributions in theory or number. It was therefore reasonable to suppose that nuclei are composed of a experiment. He developed the statis- number A of more fundamental units whose mass is very close to 1 u. Because tical laws for spin- 1/2 particles, and the only particle known at that time with a mass close to1uwastheproton in the 1930s he proposed a theory (the nucleus of hydrogen, with a mass of 1.0073 u and a charge of +e), it was of beta decay that is still used today. postulated (incorrectly, as we shall see) that the nucleus of an atom of mass He was the first to demonstrate the number A contained A protons. transmutation of elements by neutron Such a nucleus would have a nuclear charge of Ae rather than Ze; because bombardment (for which he received A > Z for all atoms heavier than hydrogen, this model gives too much positive the 1938 Nobel Prize), and he directed charge to the nucleus. This difficulty was removed by the proton-electron model, the construction of the first nuclear in which it was postulated (again incorrectly) that the nucleus also contained reactor. (A − Z) electrons. Under these assumptions, the nuclear mass would be about 12.1 | Nuclear Constituents 371 A times the mass of the proton (because the mass of the electrons is negligible) and the nuclear electric charge would be A(+e) + (A − Z)(−e) = Ze,in agreement with experiment. However, this model leads to several difficulties. First, as we discovered in Chapter 4 (see Example 4.7), the presence of electrons in the nucleus is not consistent with the uncertainty principle, which would require those electrons to have unreasonably large (∼ 19 MeV) kinetic energies. A more serious problem concerns the total intrinsic spin of the nucleus. From measurements of the very small effect of the nuclear magnetic moment on the atomic transitions (called the hyperfine splitting), we know that the proton has an intrinsic spin of 1/2, just like the electron. Consider an atom of deuterium, sometimes known as “heavy hydrogen.” It has a nuclear charge of +e, just like ordinary hydrogen, but a mass of two units, twice that of ordinary hydrogen. The proton-electron nuclear model would then require that the deuterium nucleus contain two protons and one electron, giving a net mass of two units and a net charge of one. Each of these three particles has a spin of 1/2, and the rules for adding angular momenta in quantum mechanics would lead to a spin of deuterium of either 1/2 or 3/2. However, the measured total spin of deuterium is 1. For these and other reasons, the hypothesis that electrons are a nuclear constituent must be discarded. The resolution of this dilemma came in 1932 with the discovery of the neutron, a particle of roughly the same mass as the proton (actually about 0.1% more massive) but having no electric charge. According to the proton-neutron model, a nucleus consists of Z protons and (A − Z) neutrons, giving a total charge of Ze and a total mass of roughly A times the mass of the proton, because the proton and neutron masses are roughly the same. The proton and neutron are, except for their electric charges, very similar to one another, and so they are classified together as nucleons. Some properties of the two nucleons are listed in Table 12.1. The chemical properties of any element depend on its atomic number Z, but not on its mass number A. It is possible to have two different nuclei with the same Z but with different A (that is, with the same number of protons but different numbers of neutrons). Atoms of these nuclei are identical in all their chemical properties, differing only in mass and in those properties that depend on mass. Nuclei with the same Z but different A are called isotopes. Hydrogen, for example, has three isotopes: ordinary hydrogen (Z = 1, A = 1), deuterium (Z = 1, A = 2), and tritium (Z = 1, A = 3). All of these are indicated by the chemical symbol H. When we discuss nuclear properties it is important to distinguish among the different isotopes. We do this by indicating, along with the chemical symbol, the atomic number Z, the mass number A, and the neutron number N = A − Z in the following format: A ZXN where X is any chemical symbol. The chemical symbol and the atomic number Z give the same information, so it is not necessary to include both of them in the isotope label. Also, if we specify Z then we don’t need to specify both N and TABLE 12.1 Properties of the Nucleons Name Symbol Charge Mass Rest Energy Spin + 1 Proton p e 1.007276 u 938.28 MeV /2 1 Neutron n 0 1.008665 u 939.57 MeV /2 372 Chapter 12 | Nuclear Structure and Radioactivity A. It is sufficient to give only the chemical symbol and A. The three isotopes of 1 2 3 1 hydrogen would be indicated as 1H0, 1H1, and 1H2, or more compactly as H, 2H, and 3H. In Appendix D you will find a list of isotopes and some of their properties. Example 12.1 Give the symbol for the following: (a) the isotope of helium (b) Again from the periodic table, we know that for tin with mass number 4; (b) the isotope of tin with 66 neu- (Sn), Z = 50. We are given N = 66, so A = Z + N = 116. 116 116 trons; (c) an isotope with mass number 235 that contains The symbol is 50Sn66 or Sn. 143 neutrons. (c) Given that A = 235 and N = 143, we know that = − = Solution Z A N 92. From the periodic table, we find that (a) From the periodic table, we find that helium has Z = 2. this element is uranium, and so the proper symbol for this 235 235 With A = 4, we have N = A − Z = 2. Thus the symbol isotope is 92U143 or U. 4 4 would be 2He2 or He. 12.2 NUCLEAR SIZES AND SHAPES Like atoms, nuclei lack a hard surface or an easily definable radius. In fact, different types of experiments can often reveal different values of the radius for the same nucleus.
Load more

Recommended publications
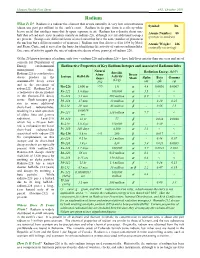
  • Radium What Is It? Radium Is a Radioactive Element That Occurs Naturally in Very Low Concentrations Symbol: Ra (About One Part Per Trillion) in the Earth’S Crust
    Human Health Fact Sheet ANL, October 2001 Radium What Is It? Radium is a radioactive element that occurs naturally in very low concentrations Symbol: Ra (about one part per trillion) in the earth’s crust. Radium in its pure form is a silvery-white heavy metal that oxidizes immediately upon exposure to air. Radium has a density about one- Atomic Number: 88 half that of lead and exists in nature mainly as radium-226, although several additional isotopes (protons in nucleus) are present. (Isotopes are different forms of an element that have the same number of protons in the nucleus but a different number of neutrons.) Radium was first discovered in 1898 by Marie Atomic Weight: 226 and Pierre Curie, and it served as the basis for identifying the activity of various radionuclides. (naturally occurring) One curie of activity equals the rate of radioactive decay of one gram (g) of radium-226. Of the 25 known isotopes of radium, only two – radium-226 and radium-228 – have half-lives greater than one year and are of concern for Department of Energy environmental Radioactive Properties of Key Radium Isotopes and Associated Radionuclides management sites. Natural Specific Radiation Energy (MeV) Radium-226 is a radioactive Abun- Decay Isotope Half-Life Activity decay product in the dance Mode Alpha Beta Gamma (Ci/g) uranium-238 decay series (%) (α) (β) (γ) and is the precursor of Ra-226 1,600 yr >99 1.0 α 4.8 0.0036 0.0067 radon-222. Radium-228 is a radioactive decay product Rn-222 3.8 days 160,000 α 5.5 < < in the thorium-232 decay Po-218 3.1 min 290 million α 6.0 < < series.
    [Show full text]
  • The Use of Cosmic-Rays in Detecting Illicit Nuclear Materials
    The use of Cosmic-Rays in Detecting Illicit Nuclear Materials Timothy Benjamin Blackwell Department of Physics and Astronomy University of Sheffield This dissertation is submitted for the degree of Doctor of Philosophy 05/05/2015 Declaration I hereby declare that except where specific reference is made to the work of others, the contents of this dissertation are original and have not been submitted in whole or in part for consideration for any other degree or qualification in this, or any other Univer- sity. This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration, except where specifically indicated in the text. Timothy Benjamin Blackwell 05/05/2015 Acknowledgements This thesis could not have been completed without the tremendous support of many people. Firstly I would like to express special appreciation and thanks to my academic supervisor, Dr Vitaly A. Kudryavtsev for his expertise, understanding and encourage- ment. I have enjoyed our many discussions concerning my research topic throughout the PhD journey. I would also like to thank my viva examiners, Professor Lee Thomp- son and Dr Chris Steer, for the time you have taken out of your schedules, so that I may take this next step in my career. Thanks must also be given to Professor Francis Liven, Professor Neil Hyatt and the rest of the Nuclear FiRST DTC team, for the initial oppor- tunity to pursue postgraduate research. Appreciation is also given to the University of Sheffield, the HEP group and EPRSC for providing me with the facilities and funding, during this work.
    [Show full text]
  • Arxiv:1904.10318V1 [Nucl-Th] 20 Apr 2019 Ucinltheory
    Nuclear structure investigation of even-even Sn isotopes within the covariant density functional theory Y. EL BASSEM1, M. OULNE2 High Energy Physics and Astrophysics Laboratory, Department of Physics, Faculty of Sciences SEMLALIA, Cadi Ayyad University, P.O.B. 2390, Marrakesh, Morocco. Abstract The current investigation aims to study the ground-state properties of one of the most interesting isotopic chains in the periodic table, 94−168Sn, from the proton drip line to the neutron drip line by using the covariant density functional theory, which is a modern theoretical tool for the description of nuclear structure phenomena. The physical observables of interest include the binding energy, separation energy, two-neutron shell gap, rms-radii for protons and neutrons, pairing energy and quadrupole deformation. The calculations are performed for a wide range of neutron numbers, starting from the proton-rich side up to the neutron-rich one, by using the density- dependent meson-exchange and the density dependent point-coupling effec- tive interactions. The obtained results are discussed and compared with available experimental data and with the already existing results of rela- tivistic Mean Field (RMF) model with NL3 functional. The shape phase transition for Sn isotopic chain is also investigated. A reasonable agreement is found between our calculated results and the available experimental data. Keywords: Ground-state properties, Sn isotopes, covariant density functional theory. arXiv:1904.10318v1 [nucl-th] 20 Apr 2019 1. INTRODUCTION In nuclear
    [Show full text]
  • Arxiv:1901.01410V3 [Astro-Ph.HE] 1 Feb 2021 Mental Information Is Available, and One Has to Rely Strongly on Theoretical Predictions for Nuclear Properties
    Origin of the heaviest elements: The rapid neutron-capture process John J. Cowan∗ HLD Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks St., Norman, OK 73019, USA Christopher Snedeny Department of Astronomy, University of Texas, 2515 Speedway, Austin, TX 78712-1205, USA James E. Lawlerz Physics Department, University of Wisconsin-Madison, 1150 University Avenue, Madison, WI 53706-1390, USA Ani Aprahamianx and Michael Wiescher{ Department of Physics and Joint Institute for Nuclear Astrophysics, University of Notre Dame, 225 Nieuwland Science Hall, Notre Dame, IN 46556, USA Karlheinz Langanke∗∗ GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany and Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany Gabriel Mart´ınez-Pinedoyy GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany; Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany; and Helmholtz Forschungsakademie Hessen f¨urFAIR, GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany Friedrich-Karl Thielemannzz Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland and GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany (Dated: February 2, 2021) The production of about half of the heavy elements found in nature is assigned to a spe- cific astrophysical nucleosynthesis process: the rapid neutron capture process (r-process). Although this idea has been postulated more than six decades ago, the full understand- ing faces two types of uncertainties/open questions: (a) The nucleosynthesis path in the nuclear chart runs close to the neutron-drip line, where presently only limited experi- arXiv:1901.01410v3 [astro-ph.HE] 1 Feb 2021 mental information is available, and one has to rely strongly on theoretical predictions for nuclear properties.
    [Show full text]
  • Two-Proton Radioactivity 2
    Two-proton radioactivity Bertram Blank ‡ and Marek P loszajczak † ‡ Centre d’Etudes Nucl´eaires de Bordeaux-Gradignan - Universit´eBordeaux I - CNRS/IN2P3, Chemin du Solarium, B.P. 120, 33175 Gradignan Cedex, France † Grand Acc´el´erateur National d’Ions Lourds (GANIL), CEA/DSM-CNRS/IN2P3, BP 55027, 14076 Caen Cedex 05, France Abstract. In the first part of this review, experimental results which lead to the discovery of two-proton radioactivity are examined. Beyond two-proton emission from nuclear ground states, we also discuss experimental studies of two-proton emission from excited states populated either by nuclear β decay or by inelastic reactions. In the second part, we review the modern theory of two-proton radioactivity. An outlook to future experimental studies and theoretical developments will conclude this review. PACS numbers: 23.50.+z, 21.10.Tg, 21.60.-n, 24.10.-i Submitted to: Rep. Prog. Phys. Version: 17 December 2013 arXiv:0709.3797v2 [nucl-ex] 23 Apr 2008 Two-proton radioactivity 2 1. Introduction Atomic nuclei are made of two distinct particles, the protons and the neutrons. These nucleons constitute more than 99.95% of the mass of an atom. In order to form a stable atomic nucleus, a subtle equilibrium between the number of protons and neutrons has to be respected. This condition is fulfilled for 259 different combinations of protons and neutrons. These nuclei can be found on Earth. In addition, 26 nuclei form a quasi stable configuration, i.e. they decay with a half-life comparable or longer than the age of the Earth and are therefore still present on Earth.
    [Show full text]
  • 2.3 Neutrino-Less Double Electron Capture - Potential Tool to Determine the Majorana Neutrino Mass by Z.Sujkowski, S Wycech
    DEPARTMENT OF NUCLEAR SPECTROSCOPY AND TECHNIQUE 39 The above conservatively large systematic hypothesis. TIle quoted uncertainties will be soon uncertainty reflects the fact that we did not finish reduced as our analysis progresses. evaluating the corrections fully in the current analysis We are simultaneously recording a large set of at the time of this writing, a situation that will soon radiative decay events for the processes t e'v y change. This result is to be compared with 1he and pi-+eN v y. The former will be used to extract previous most accurate measurement of McFarlane the ratio FA/Fv of the axial and vector form factors, a et al. (Phys. Rev. D 1984): quantity of great and longstanding interest to low BR = (1.026 ± 0.039)'1 I 0 energy effective QCD theory. Both processes are as well as with the Standard Model (SM) furthermore very sensitive to non- (V-A) admixtures in prediction (Particle Data Group - PDG 2000): the electroweak lagLangian, and thus can reveal BR = (I 038 - 1.041 )*1 0-s (90%C.L.) information on physics beyond the SM. We are currently analyzing these data and expect results soon. (1.005 - 1.008)* 1W') - excl. rad. corr. Tale 1 We see that even working result strongly confirms Current P1IBETA event sxpelilnentstatistics, compared with the the validity of the radiative corrections. Another world data set. interesting comparison is with the prediction based on Decay PIBETA World data set the most accurate evaluation of the CKM matrix n >60k 1.77k element V d based on the CVC hypothesis and ihce >60 1.77_ _ _ results
    [Show full text]
  • Problem Set 3 Solutions
    22.01 Fall 2016, Problem Set 3 Solutions October 9, 2016 Complete all the assigned problems, and do make sure to show your intermediate work. 1 Activity and Half Lives 1. Given the half lives and modern-day abundances of the three natural isotopes of uranium, calculate the isotopic fractions of uranium when the Earth first formed 4.5 billion years ago. Today, uranium consists of 0.72% 235U, 99.2745% 238U, and 0.0055% 234U. However, it is clear that the half life of 234U (245,500 years) is so short compared to the lifetime of the Earth (4,500,000,000 years) that it would have all decayed away had there been some during the birth of the Earth. Therefore, we look a little closer, and find that 234U is an indirect decay product of 238U, by tracing it back from its parent nuclides on the KAERI table: α β− β− 238U −! 234T h −! 234P a −! 234U (1) Therefore we won’t consider there being any more 234U than would normally be in equi­ librium with the 238U around at the time. We set up the two remaining equations as follows: −t t ;235 −t t ;238 = 1=2 = 1=2 N235 = N0235 e N238 = N0238 e (2) Using the current isotopic abundances from above as N235 and N238 , the half lives from n 9 t 1 1 the KAERI Table of Nuclides t =2;235 = 703800000 y; t =2;238 = 4:468 · 10 y , and the lifetime of the earth in years (keeping everything in the same units), we arrive at the following expressions for N0235 and N0238 : N235 0:0072 N238 0:992745 N0235 =−t = 9 = 4:307N0238 =−t = 9 = 2:718 (3) =t1 ;235 −4:5·10 =7:038·108 =t1 ;238 −4:5·10 =4:468·109 e =2 e e =2 e Finally, taking the ratios of these two relative abundances gives us absolute abundances: 4:307 2:718 f235 = = 0:613 f238 = = 0:387 (4) 4:307 + 2:718 4:307 + 2:718 235U was 61.3% abundant, and 238U was 38.7% abundant.
    [Show full text]
  • Abundance and Radioactivity of Unstable Isotopes
    5 RADIONUCLIDE DECAY AND PRODUCTION This section contains a brief review of relevant facts about radioactivity, i.e. the phenomenon of nuclear decay, and about nuclear reactions, the production of nuclides. For full details the reader is referred to textbooks on nuclear physics and radiochemistry, and on the application of radioactivity in the earth sciences (cited in the list of references). 5.1 NUCLEAR INSTABILITY If a nucleus contains too great an excess of neutrons or protons, it will sooner or later disintegrate to form a stable nucleus. The different modes of radioactive decay will be discussed briefly. The various changes that can take place in the nucleus are shown in Fig.5.1 In transforming into a more stable nucleus, the unstable nucleus looses potential energy, part of its binding energy. This energy Q is emitted as kinetic energy and is shared by the particles formed according to the laws of conservation of energy and momentum (see Sect.5.3). The energy released during nuclear decay can be calculated from the mass budget of the decay reaction, using the equivalence of mass and energy, discussed in Sect.2.4. The atomic mass determinations have been made very accurately and precisely by mass spectrometric measurement: 2 E = [Mparent Mdaughter] P mc (5.1) with 1 amu V 931.5 MeV (5.2) Disintegration of a parent nucleus produces a daughter nucleus which generally is in an excited state. After an extremely short time the daughter nucleus looses the excitation energy through the emittance of one or more (gamma) rays, electromagnetic radiation with a very short wavelength, similar to the emission of light (also electromagnetic radiation , but with a longer wavelength) by atoms which have been brought into an excited state.
    [Show full text]
  • Two-Proton Decay Energy and Width of 19Mg(G.S.)
    University of Pennsylvania ScholarlyCommons Department of Physics Papers Department of Physics 7-30-2007 Two-Proton Decay Energy and Width of 19Mg(g.s.) H. Terry Fortune University of Pennsylvania, [email protected] Rubby Sherr Princeton University Follow this and additional works at: https://repository.upenn.edu/physics_papers Part of the Physics Commons Recommended Citation Fortune, H. T., & Sherr, R. (2007). Two-Proton Decay Energy and Width of 19Mg(g.s.). Retrieved from https://repository.upenn.edu/physics_papers/171 Suggested Citation: H.T. Fortune and R. Sherr. (2007). Two-proton decay energy and width of 19Mg(g.s.). Physical Review C 76, 014313. © 2007 The American Physical Society http://dx.doi.org/10.1103/PhysRevC.76.014313 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/physics_papers/171 For more information, please contact [email protected]. Two-Proton Decay Energy and Width of 19Mg(g.s.) Abstract We use a weak-coupling procedure and results of a shell-model calculation to compute the two-proton separation energy of 19Mg. Our result is at the upper end of the previous range, but 19Mg is still bound for single proton decay to 18Na. We also calculate the 2p decay width. Disciplines Physical Sciences and Mathematics | Physics Comments Suggested Citation: H.T. Fortune and R. Sherr. (2007). Two-proton decay energy and width of 19Mg(g.s.). Physical Review C 76, 014313. © 2007 The American Physical Society http://dx.doi.org/10.1103/PhysRevC.76.014313 This journal article is available at ScholarlyCommons: https://repository.upenn.edu/physics_papers/171 PHYSICAL REVIEW C 76, 014313 (2007) Two-proton decay energy and width of 19Mg(g.s.) H.
    [Show full text]
  • Range of Usefulness of Bethe's Semiempirical Nuclear Mass Formula
    RANGE OF ..USEFULNESS OF BETHE' S SEMIEMPIRIC~L NUCLEAR MASS FORMULA by SEKYU OBH A THESIS submitted to OREGON STATE COLLEGE in partial fulfillment or the requirements tor the degree of MASTER OF SCIENCE June 1956 TTPBOTTDI Redacted for Privacy lrrt rtllrt ?rsfirror of finrrtor Ia Ohrr;r ef lrJer Redacted for Privacy Redacted for Privacy 0hrtrurn of tohoot Om0qat OEt ttm Redacted for Privacy Dru of 0rrdnrtr Sohdbl Drta thrrlr tr prrrEtrl %.ifh , 1,,r, ," r*(,-. ttpo{ by Brtty Drvlr ACKNOWLEDGMENT The author wishes to express his sincere appreciation to Dr. G. L. Trigg for his assistance and encouragement, without which this study would not have been concluded. The author also wishes to thank Dr. E. A. Yunker for making facilities available for these calculations• • TABLE OF CONTENTS Page INTRODUCTION 1 NUCLEAR BINDING ENERGIES AND 5 SEMIEMPIRICAL MASS FORMULA RESEARCH PROCEDURE 11 RESULTS 17 CONCLUSION 21 DATA 29 f BIBLIOGRAPHY 37 RANGE OF USEFULNESS OF BETHE'S SEMIEMPIRICAL NUCLEAR MASS FORMULA INTRODUCTION The complicated experimental results on atomic nuclei haYe been defying definite interpretation of the structure of atomic nuclei for a long tfme. Even though Yarious theoretical methods have been suggested, based upon the particular aspects of experimental results, it has been impossible to find a successful theory which suffices to explain the whole observed properties of atomic nuclei. In 1936, Bohr (J, P• 344) proposed the liquid drop model of atomic nuclei to explain the resonance capture process or nuclear reactions. The experimental evidences which support the liquid drop model are as follows: 1. Substantially constant density of nuclei with radius R - R Al/3 - 0 (1) where A is the mass number of the nucleus and R is the constant of proportionality 0 with the value of (1.5! 0.1) x 10-lJcm~ 2.
    [Show full text]
  • "Indoor Radon and Radon Decay Product Measurement Device Protocols"
    "Indoor Radon and Radon Decay Product Measurement Device Protocols" U.S. Environmental Protection Agency Office of Air and Radiation (6604J) EPA 402-R-92-004, July 1992 (revised) Table of Contents Disclaimer Acknowledgements Significant Changes in This Revision Radon and Radon Decay Product Measurement Methods Section 1: General Considerations 1.1 Introduction and Background 1.2 General Guidance on Measurement Strategy, Measurement Conditions, Device Location Selection, and Documentation 1.3 Quality Assurance Section 2: Indoor Radon Measurement Device Protocols 2.1 Protocol for Using Continuous Radon Monitors (CR) to Measure Indoor Radon Concentrations 2.2 Protocol for Using Alpha Track Detectors (AT or ATD) to Measure Indoor Radon Concentrations 2.4 Protocol for Using Activated Charcoal Adsorption Devices (AC) to Measure Indoor Radon Concentrations 2.5 Protocol for Using Charcoal Liquid Scintillation (LS) Devices to Measure Indoor Radon Concentrations 2.6 Protocol for Using Grab Radon Sampling (GB, GC, GS), Pump/Collapsible Bag Devices (PB), and Three-Day Integrating Evacuated Scintillation Cells (SC) to Measure Indoor Radon Concentrations 2.7 Interim Protocol for Using Unfiltered Track Detectors (UT) to Measure Indoor Radon Concentrations Section 3: Indoor Radon Decay Product Measurement Device Protocols 3.1 Protocol for Using Continuous Working Level Monitors (CW) to Measure Indoor Radon Decay Product Concentrations 3.2 Protocol for Using Radon Progeny Integrating Sampling Units (RPISU or RP) to Measure Indoor Radon Decay Product Concentrations 3.3 Protocol for Using Grab Sampling-Working Level (GW) to Measure Indoor Radon Decay Product Concentrations Glossary References Please Note: EPA closed its National Radon Proficiency Program (RPP) in 1998.
    [Show full text]
  • Energy What Is a Nuclear Reaction?
    4/16/2016 Option C: Energy C.3 : Nuclear Fusion and Fission What is a nuclear reaction? • A nuclear reaction is any reaction that involves the nucleus. • These reactions change the identity of an atom, as opposed to chemical reactions which only involve valence electrons. 1 4/16/2016 The nucleus • The nucleus is made up of protons and neutrons. • We know what the protons do – they provide an electrostatic attraction to the electrons close… but what about the neutrons? The Neutrons • The major function of the neutrons is to hold the nucleus together. • The neutrons provide a strong nuclear force of attraction within the nucleus, counteracting the repulsion between the positively charged protons. 2 4/16/2016 How is the nucleus held together? • In the 1930’s it was first observed that the mass of an atoms nucleus is less than the sum of the masses of the protons + neutrons…? • Some of the mass of the nucleus is converted into energy to hold the nucleus together. 3 4/16/2016 Mass Defect • The difference in mass of the nucleus and it’s parts is referred to as the mass defect, and the energy (e=mc 2) it provided is called the nuclear binding energy. 4 4/16/2016 Nuclear vs. Chemical Reactions • This nuclear binding energy is released during nuclear reactions (fission & fusion), and is ~1,000,000X greater than the chemical bond energy released during chemical reactions. What makes an isotope radioactive? • Elements are radioactive when their nucleus is unstable. • The stabilizing force of the neutrons is effective for smaller elements, though all elements above lead are radioactive.
    [Show full text]