DOCSLIB.ORG

Calculating Beta Decay for the R Process

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Calculating Beta Decay for the R Process Calculating β Decay for the r Process J. Engel with M. Mustonen, T. Shafer C. Fröhlich, G. McLaughlin, M. Mumpower, R. Surman D. Gambacurta, M. Grasso January 18, 2017 R-Process Abundances β decay is particularly important. Responsible for increasing Z throughout r process, and its competition with neutron capture during freeze-out can have large effect on abundances. Nuclear Landscape 126 Limits of nuclear existence To convincingly locate the 82 site(s) of the r process, we r-process need to know reaction 50 rates and properties in protons 82 28 rp-process very neutron-rich nuclei. 20 50 8 28 neutrons Density Functional Theory 2 20 Selfconsistent Mean Field 2 8 A=10 A~60 A=12 0Ñω Shell Towards a unified Ab initio Model description of the nucleus few-body calculations No-Core Shell Model G-matrix Nuclear Landscape 126 Limits of nuclear existence To convincingly locate the 82 site(s) of the r process, we r-process need to know reaction 50 rates and properties in protons 82 28 rp-process very neutron-rich nuclei. 20 50 8 28 neutrons Density Functional Theory 2 20 Selfconsistent Mean Field 2 8 A=10 A~60 A=12 β decay is particularly important. Responsible0Ñω Shell for increasingTowards aZ unified Ab initio Model description of the nucleus throughout r process, and its competitionfew-body with neutron capture calculations No-Core Shell Model during freeze-out can have large effectG-matrix on abundances. So nuclear structure model must do good job with masses, spectra, and wave functions, in many isotopes. Calculating β Decay is Hard Though, As We’ll See, It Gets a Bit Easier in Neutron-Rich Nuclei To calculate β decay between two states, you need: an accurate value for the decay energy ∆E (since contribution to rate ∆E5 for “allowed” decay). / matrix elements of the decay operator στ- and “forbidden" operators rτ-; rστ- between the two states. The operator τ- turns a neutron into a proton; the allowed decay operator does that while flipping spin. Most of the time the decay operator leaves you above threshold, by the way. Calculating β Decay is Hard Though, As We’ll See, It Gets a Bit Easier in Neutron-Rich Nuclei To calculate β decay between two states, you need: an accurate value for the decay energy ∆E (since contribution to rate ∆E5 for “allowed” decay). / matrix elements of the decay operator στ- and “forbidden" operators rτ-; rστ- between the two states. The operator τ- turns a neutron into a proton; the allowed decay operator does that while flipping spin. Most of the time the decay operator leaves you above threshold, by the way. So nuclear structure model must do good job with masses, spectra, and wave functions, in many isotopes. What’s Usually Been Used for β-Decay in Simulations Ⱥ ÅÓÐ ÐÖ¸ º È«Ö¸ ú¹Äº ÃÖØÞ »ËÔÒ ÙÔ Ø Ð Ö¹ÔÖÓ ×× º º º ½½ Möller, Pfeiffer, Kratz (2003) 104 β− Ancient but Still in Some Ways 103 decay (Theory: GT) Unsurpassed Technology 102 101 Masses through “finite-range 100 − droplet model with shell 10 1 − 2 10 Total Error = 3.73 for 184 nuclei, Tβ,exp < 1 s ,exp corrections.” β Total Error = 21.16 for 546 nuclei (13 clipped), Tβ < 1000 s − 3 ,exp T / 10 4 10 “QRPA” with simple ,calc − β 3 β decay (Theory: GT + ff) space-independent interaction. T 10 102 First forbidden decay 101 (correction due to finite nuclear 100 − size) added very crude way in 10 1 − 2 2003. Shortens half lives. 10 Total Error = 3.08 for 184 nuclei, Tβ,exp < 1 s Total Error = 4.82 for 546 nuclei, Tβ,exp < 1000 s − 10 3 − − − 10 3 10 2 10 1 100 101 102 103 Experimental β-Decay Half-life Tβ,exp (s) ½6 ÙÖ ÊØÓ Ó ØÓ ÜÔ ÖÑÒØÐ ¬ Ý Ð¹ÐÚ× ÓÖ ÖÓÑ Ç ØÓ Ø Ú×Ø ÒÓÛÒ Ò ÓÙÖ ÔÖÚÓÙ× Ò ÑÓ Ð׺ ÖÖÓÖ× ØÖ Ö ÑÒÝ ÑÓÖ Ô ÓÒØ× ØÒ ÓÖ ÐÖ ÖÖÓÖ׺ Ì× × ÒÓØ ×Ò Ò Ø ¬ÙÖ׸ ÓÖ ×ÑÐÐ ÖÖÓÖ× ÑÒÝ Ô ÓÒØ× Ö ×ÙÔ ÖÑÔ Ó× ÓÒ ÓÒ ÒÓØÖº ÌÓ ÓØÒ ÑÓÖ ÙÒÖ×ØÒÒ Ó Ø ÖÖÓÖ Ò Ø Û ØÖÓÖ Ô ÖÓÖÑ ÑÓÖ ØÐ ÒÐÝ×׺ ÇÒ ÓØÒ ÒÐÝÞ× Ø ÖÖÓÖ Ò Ý ×ØÙÝÒ ÖÓ ÓعÑÒ¹×ÕÙÖ ´ÖÑ×µ ÚØÓÒ¸ Ò Ø× ÛÓÙÐ Ò X ½ ¾ ¾ ´Ì Ì µ ´½¿µ ÖÑ× ¬ ;ÜÔ ¬ ; Ò i½ ÀÓÛÚÖ¸ Ò ÖÖÓÖ ÒÐÝ×× × ÙÒ×ÙØÐ Ö¸ ÓÖ ØÛÓ Ö×ÓÒ׺ Ö×ظ Ø ÕÙÒØØ× ×ØÙ Modern Alternative: Skyrme Dens.-Func. Theory Started as zero-range effective potential, treated in mean-field theory: VSkyrme = t0 (1 + x0Pσ) δ(r1 - r2) 1 h 2 i + t (1 + x Pσ) (r - r ) δ(r - r ) + h:c: 2 1 1 1 2 1 2 + t (1 + x Pσ)(r - r ) δ(r - r )(r - r ) 2 2 1 2 · 1 2 1 2 1 α + t (1 + x Pσ) δ(r - r )ρ ([r + r ]=2) 6 3 3 1 2 1 2 + iW (σ + σ ) (r - r ) δ(r - r )(r - r ) 0 1 2 · 1 2 × 1 2 1 2 1+σ1 σ2 where Pσ · . ≡ 2 Re-framed as density functional, which can then be extended: 3 E = d r Heven + Hodd +Hkin. + Hem Z HSkyrme Hodd has no effect in mean-field| {z description} of time-reversal even states (e.g. ground states), but large effect in β decay. Time-Even and Time-Odd Parts of Functional Not including pairing: 1 t ρ 2 ∆ρ 2 τ Heven = C ρ + C ρtt ρtt + C ρtt τtt t tt3 t 3 r 3 t 3 3 = t =-t Xt 0 3X J J 2 + Cr ρtt r Jtt + C J t 3 · 3 t tt3 1 t s 2 ∆s 2 T j 2 H = C s + C stt stt + C stt Ttt + C j odd t tt3 t 3 · r 3 t 3 · 3 t tt3 = t =-t Xt 0 3X j F s 2 + Cr s r j + C s F + Cr (r s ) t tt3 · × tt3 t tt3 · tt3 t · tt3 Time-even densities: ρ = usual density τ = kinetic density J = spin-orbit current Time-odd densities: s = spin current T = kinetic spin current j = usual current Couplings are connected by “Skyrme interaction,” but can be set independently if working directly with density-functional. Starting Point: Mean-Field-Like Calculation (HFB) Gives you ground state density, etc. This is where Skyrme functionals have made their living. Zr-102: normal density and pairing density HFB, 2-D lattice, SLy4 + volume pairing Ref: Artur Blazkiewicz, Vanderbilt, Ph.D. thesis (2005) G3H G3H G=HD !βT bREVU! #@3D !βT bREVTGWH!C! PEE!G91%!#6!)EC!&A5E!#8E!U!GTRRXH! TFTXFSR! 2)(#4! #4!(#4C!1"#4 ')6! `! QRPA QRPA done properly is time-dependent HFB with small harmonic perturbation. Perturbing operator is β-decay transition operator. Decay matrix elements obtained from response of nucleus to perturbation. Schematic QRPA of Möller et al. is very simplified version of this. No fully self-consistent mean-field calculation to start. Nucleon-nucleon interaction is schematic. Initial Skyrme Application: Spherical QRPA 126 Limits of nuclear existence 82 r-process 50 protons 82 28 rp-process 20 50 8 28 neutrons Density Functional Theory 2 20 Selfconsistent Mean Field 2 8 A=10 A~60 A=12 0Ñω Shell Towards a unified Ab initio Model description of the nucleus few-body calculations No-Core Shell Model G-matrix Closed shell nuclei are spherical. One free parameter: strength of proton-neutron spin-1 pairing (it’s zero in 102 schematic QRPA.) Adjusted in each of the 101 t 2 p / x 1 three peak regions to reproduce measured e T / c 0 2 l / a 10 1 lifetimes. c T 10-1 80Zn 78Zn 76Zn -2 10 82Ge 0 50 100 150 200 250 300 350 V0 [MeV] Initial Skyrme Application: Spherical QRPA 25 90 In nuclei near “waiting points,” with no Zr forbidden decay. 20 ) 15 T G ( Chose functional corresponding to B 10 Skyrme interaction SkO0 because did best with GT distributions. 5 SkO' SLy5 SkP Expt 0 0 2 4 6 8 10 12 14 16 18 20 excitation energy [MeV] 102 101 t 2 p / x 1 e T / c 0 2 l / a 10 1 c T 10-1 80Zn 78Zn 76Zn -2 10 82Ge 0 50 100 150 200 250 300 350 V0 [MeV] Initial Skyrme Application: Spherical QRPA 25 90 In nuclei near “waiting points,” with no Zr forbidden decay. 20 ) 15 T G ( Chose functional corresponding to B 10 Skyrme interaction SkO0 because did best with GT distributions. 5 SkO' SLy5 SkP Expt 0 0 2 4 6 8 10 12 14 16 18 20 excitation energy [MeV] One free parameter: strength of proton-neutron spin-1 pairing (it’s zero in schematic QRPA.) Adjusted in each of the three peak regions to reproduce measured lifetimes. Re [S(ω)f(ω)] Im [S(ω)f(ω)] Im ω Im ω Beta-decay rates obtained C C by integrating strength with phase-space Re ω Re ω weighting function in contour around excited states below threshold. New: Fast Skyrme QRPA in Deformed Nuclei Finite-Amplitude Method 7 12 128 208 ] K , Cd =0 1 ] Pb K =0, 1 1 ± 1 ± − 6 − 9 5 4 6 3 Strength functions 2 3 GT strength [MeV 1 GT strength [MeV 0 0 computed directly, in 7 146 7 166 K K ] Ba =0 ] Gd =0 1 1 − 6 − 6 orders of magnitude less 5 5 4 4 3 3 time than with matrix 2 2 GT strength [MeV 1 GT strength [MeV 1 0 0 ] 7 146 ] 7 166 QRPA.
Load more

Recommended publications
  • Arxiv:1901.01410V3 [Astro-Ph.HE] 1 Feb 2021 Mental Information Is Available, and One Has to Rely Strongly on Theoretical Predictions for Nuclear Properties
    Origin of the heaviest elements: The rapid neutron-capture process John J. Cowan∗ HLD Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks St., Norman, OK 73019, USA Christopher Snedeny Department of Astronomy, University of Texas, 2515 Speedway, Austin, TX 78712-1205, USA James E. Lawlerz Physics Department, University of Wisconsin-Madison, 1150 University Avenue, Madison, WI 53706-1390, USA Ani Aprahamianx and Michael Wiescher{ Department of Physics and Joint Institute for Nuclear Astrophysics, University of Notre Dame, 225 Nieuwland Science Hall, Notre Dame, IN 46556, USA Karlheinz Langanke∗∗ GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany and Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany Gabriel Mart´ınez-Pinedoyy GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany; Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany; and Helmholtz Forschungsakademie Hessen f¨urFAIR, GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany Friedrich-Karl Thielemannzz Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland and GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany (Dated: February 2, 2021) The production of about half of the heavy elements found in nature is assigned to a spe- cific astrophysical nucleosynthesis process: the rapid neutron capture process (r-process). Although this idea has been postulated more than six decades ago, the full understand- ing faces two types of uncertainties/open questions: (a) The nucleosynthesis path in the nuclear chart runs close to the neutron-drip line, where presently only limited experi- arXiv:1901.01410v3 [astro-ph.HE] 1 Feb 2021 mental information is available, and one has to rely strongly on theoretical predictions for nuclear properties.
    [Show full text]
  • Two-Proton Radioactivity 2
    Two-proton radioactivity Bertram Blank ‡ and Marek P loszajczak † ‡ Centre d’Etudes Nucl´eaires de Bordeaux-Gradignan - Universit´eBordeaux I - CNRS/IN2P3, Chemin du Solarium, B.P. 120, 33175 Gradignan Cedex, France † Grand Acc´el´erateur National d’Ions Lourds (GANIL), CEA/DSM-CNRS/IN2P3, BP 55027, 14076 Caen Cedex 05, France Abstract. In the first part of this review, experimental results which lead to the discovery of two-proton radioactivity are examined. Beyond two-proton emission from nuclear ground states, we also discuss experimental studies of two-proton emission from excited states populated either by nuclear β decay or by inelastic reactions. In the second part, we review the modern theory of two-proton radioactivity. An outlook to future experimental studies and theoretical developments will conclude this review. PACS numbers: 23.50.+z, 21.10.Tg, 21.60.-n, 24.10.-i Submitted to: Rep. Prog. Phys. Version: 17 December 2013 arXiv:0709.3797v2 [nucl-ex] 23 Apr 2008 Two-proton radioactivity 2 1. Introduction Atomic nuclei are made of two distinct particles, the protons and the neutrons. These nucleons constitute more than 99.95% of the mass of an atom. In order to form a stable atomic nucleus, a subtle equilibrium between the number of protons and neutrons has to be respected. This condition is fulfilled for 259 different combinations of protons and neutrons. These nuclei can be found on Earth. In addition, 26 nuclei form a quasi stable configuration, i.e. they decay with a half-life comparable or longer than the age of the Earth and are therefore still present on Earth.
    [Show full text]
  • 2.3 Neutrino-Less Double Electron Capture - Potential Tool to Determine the Majorana Neutrino Mass by Z.Sujkowski, S Wycech
    DEPARTMENT OF NUCLEAR SPECTROSCOPY AND TECHNIQUE 39 The above conservatively large systematic hypothesis. TIle quoted uncertainties will be soon uncertainty reflects the fact that we did not finish reduced as our analysis progresses. evaluating the corrections fully in the current analysis We are simultaneously recording a large set of at the time of this writing, a situation that will soon radiative decay events for the processes t e'v y change. This result is to be compared with 1he and pi-+eN v y. The former will be used to extract previous most accurate measurement of McFarlane the ratio FA/Fv of the axial and vector form factors, a et al. (Phys. Rev. D 1984): quantity of great and longstanding interest to low BR = (1.026 ± 0.039)'1 I 0 energy effective QCD theory. Both processes are as well as with the Standard Model (SM) furthermore very sensitive to non- (V-A) admixtures in prediction (Particle Data Group - PDG 2000): the electroweak lagLangian, and thus can reveal BR = (I 038 - 1.041 )*1 0-s (90%C.L.) information on physics beyond the SM. We are currently analyzing these data and expect results soon. (1.005 - 1.008)* 1W') - excl. rad. corr. Tale 1 We see that even working result strongly confirms Current P1IBETA event sxpelilnentstatistics, compared with the the validity of the radiative corrections. Another world data set. interesting comparison is with the prediction based on Decay PIBETA World data set the most accurate evaluation of the CKM matrix n >60k 1.77k element V d based on the CVC hypothesis and ihce >60 1.77_ _ _ results
    [Show full text]
  • Problem Set 3 Solutions
    22.01 Fall 2016, Problem Set 3 Solutions October 9, 2016 Complete all the assigned problems, and do make sure to show your intermediate work. 1 Activity and Half Lives 1. Given the half lives and modern-day abundances of the three natural isotopes of uranium, calculate the isotopic fractions of uranium when the Earth first formed 4.5 billion years ago. Today, uranium consists of 0.72% 235U, 99.2745% 238U, and 0.0055% 234U. However, it is clear that the half life of 234U (245,500 years) is so short compared to the lifetime of the Earth (4,500,000,000 years) that it would have all decayed away had there been some during the birth of the Earth. Therefore, we look a little closer, and find that 234U is an indirect decay product of 238U, by tracing it back from its parent nuclides on the KAERI table: α β− β− 238U −! 234T h −! 234P a −! 234U (1) Therefore we won’t consider there being any more 234U than would normally be in equi­ librium with the 238U around at the time. We set up the two remaining equations as follows: −t t ;235 −t t ;238 = 1=2 = 1=2 N235 = N0235 e N238 = N0238 e (2) Using the current isotopic abundances from above as N235 and N238 , the half lives from n 9 t 1 1 the KAERI Table of Nuclides t =2;235 = 703800000 y; t =2;238 = 4:468 · 10 y , and the lifetime of the earth in years (keeping everything in the same units), we arrive at the following expressions for N0235 and N0238 : N235 0:0072 N238 0:992745 N0235 =−t = 9 = 4:307N0238 =−t = 9 = 2:718 (3) =t1 ;235 −4:5·10 =7:038·108 =t1 ;238 −4:5·10 =4:468·109 e =2 e e =2 e Finally, taking the ratios of these two relative abundances gives us absolute abundances: 4:307 2:718 f235 = = 0:613 f238 = = 0:387 (4) 4:307 + 2:718 4:307 + 2:718 235U was 61.3% abundant, and 238U was 38.7% abundant.
    [Show full text]
  • Abundance and Radioactivity of Unstable Isotopes
    5 RADIONUCLIDE DECAY AND PRODUCTION This section contains a brief review of relevant facts about radioactivity, i.e. the phenomenon of nuclear decay, and about nuclear reactions, the production of nuclides. For full details the reader is referred to textbooks on nuclear physics and radiochemistry, and on the application of radioactivity in the earth sciences (cited in the list of references). 5.1 NUCLEAR INSTABILITY If a nucleus contains too great an excess of neutrons or protons, it will sooner or later disintegrate to form a stable nucleus. The different modes of radioactive decay will be discussed briefly. The various changes that can take place in the nucleus are shown in Fig.5.1 In transforming into a more stable nucleus, the unstable nucleus looses potential energy, part of its binding energy. This energy Q is emitted as kinetic energy and is shared by the particles formed according to the laws of conservation of energy and momentum (see Sect.5.3). The energy released during nuclear decay can be calculated from the mass budget of the decay reaction, using the equivalence of mass and energy, discussed in Sect.2.4. The atomic mass determinations have been made very accurately and precisely by mass spectrometric measurement: 2 E = [Mparent Mdaughter] P mc (5.1) with 1 amu V 931.5 MeV (5.2) Disintegration of a parent nucleus produces a daughter nucleus which generally is in an excited state. After an extremely short time the daughter nucleus looses the excitation energy through the emittance of one or more (gamma) rays, electromagnetic radiation with a very short wavelength, similar to the emission of light (also electromagnetic radiation , but with a longer wavelength) by atoms which have been brought into an excited state.
    [Show full text]
  • Two-Proton Decay Energy and Width of 19Mg(G.S.)
    University of Pennsylvania ScholarlyCommons Department of Physics Papers Department of Physics 7-30-2007 Two-Proton Decay Energy and Width of 19Mg(g.s.) H. Terry Fortune University of Pennsylvania, [email protected] Rubby Sherr Princeton University Follow this and additional works at: https://repository.upenn.edu/physics_papers Part of the Physics Commons Recommended Citation Fortune, H. T., & Sherr, R. (2007). Two-Proton Decay Energy and Width of 19Mg(g.s.). Retrieved from https://repository.upenn.edu/physics_papers/171 Suggested Citation: H.T. Fortune and R. Sherr. (2007). Two-proton decay energy and width of 19Mg(g.s.). Physical Review C 76, 014313. © 2007 The American Physical Society http://dx.doi.org/10.1103/PhysRevC.76.014313 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/physics_papers/171 For more information, please contact [email protected]. Two-Proton Decay Energy and Width of 19Mg(g.s.) Abstract We use a weak-coupling procedure and results of a shell-model calculation to compute the two-proton separation energy of 19Mg. Our result is at the upper end of the previous range, but 19Mg is still bound for single proton decay to 18Na. We also calculate the 2p decay width. Disciplines Physical Sciences and Mathematics | Physics Comments Suggested Citation: H.T. Fortune and R. Sherr. (2007). Two-proton decay energy and width of 19Mg(g.s.). Physical Review C 76, 014313. © 2007 The American Physical Society http://dx.doi.org/10.1103/PhysRevC.76.014313 This journal article is available at ScholarlyCommons: https://repository.upenn.edu/physics_papers/171 PHYSICAL REVIEW C 76, 014313 (2007) Two-proton decay energy and width of 19Mg(g.s.) H.
    [Show full text]
  • CHAPTER 2 the Nucleus and Radioactive Decay
    1 CHEMISTRY OF THE EARTH CHAPTER 2 The nucleus and radioactive decay 2.1 The atom and its nucleus An atom is characterized by the total positive charge in its nucleus and the atom’s mass. The positive charge in the nucleus is Ze , where Z is the total number of protons in the nucleus and e is the charge of one proton. The number of protons in an atom, Z, is known as the atomic number and dictates which element an atom represents. The nucleus is also made up of N number of neutrally charged particles of similar mass as the protons. These are called neutrons . The combined number of protons and neutrons, Z+N , is called the atomic mass number A. A specific nuclear species, or nuclide , is denoted by A Z Γ 2.1 where Γ represents the element’s symbol. The subscript Z is often dropped because it is redundant if the element’s symbol is also used. We will soon learn that a mole of protons and a mole of neutrons each have a mass of approximately 1 g, and therefore, the mass of a mole of Z+N should be very close to an integer 1. However, if we look at a periodic table, we will notice that an element’s atomic weight, which is the mass of one mole of its atoms, is rarely close to an integer. For example, Iridium’s atomic weight is 192.22 g/mole. The reason for this discrepancy is that an element’s neutron number N can vary.
    [Show full text]
  • RIA, Beta Decay and the R-Process
    Preliminaries So Far Future Beta Decay, the R Process, RIA J. Engel April 4, 2006 Preliminaries So Far Future 1 Beta Decay is Important, Hard 2 What’s Been Done So Far 3 Future Work Preliminaries So Far Future Beta-Decay Far From Stability is Important 126 Limits of nuclear existence Half-lives are particularly 82 important at the r-process r-process “ladders” (N=50, 82, 126) 50 protons 82 ry where abundances peak. These d 28 rp-process 20 ctional Theo half-lives determine the 50 t Mean Fiel 8 28 neutrons Density Fun r-process time scale. 2 20 Selfconsisten 2 8 A=10 A~60 A=12 But others are also important; 0Ñω Shell Towards a unified affect abundances between Ab initio Model description of the nucleus few-body peaks. calculations No-Core Shell Model G-matrix Yes, uncertainties in astrophysics dwarf those in nuclear physics, but we won’t really understand the nucleosynthesis until both are reduced. 5 Preliminaries So Far Future Calculating Beta Decay is Hard. (though it gets easier in neutron-rich nuclei). To calculate beta decay between two states, you need: an accurate value for the decay energy ∆E (since −5 T1/2 ∝ ∆E ) matrix elements of the GT operator ~στ− and (sometimes) “forbidden” operators ~r~στ− between the two states .[Most of the strength of is above threshold, btw]. So your nuclear structure model must do a good job with nuclear masses, spectra, and wave functions, and to simulate the r process it must do the job in almost all isotopes.
    [Show full text]
  • Enhancement Mechanisms of Low Energy Nuclear Reactions
    Enhancement Mechanisms of Low Energy Nuclear Reactions Gareev F.A., Zhidkova I.E. Joint Institute for Nuclear Research, 141980, Dubna, Russia [email protected] [email protected] 1 Introduction One of the fundamental presentations of nuclear physics since the very early days of its study has been the common assumption that the radioactive process (the half-life or decay constant) is independent of external conditions. Rutherford, Chadwick and Ellis [1] came to the conclusion that: • ≪the value of λ (the decay constant) for any substance is a characteristic constant inde- pendent of all physical and chemical conditions≫. This very important conclusion (still playing a negative role in cold fusion phenomenon) is based on the common expectation (P. Curie suggested that the decay constant is the etalon of time) and observation that the radioactivity is a nuclear phenomenon since all our actions affect only states of the atom but do not change the nucleus states. We cannot hope to mention even a small part of the work done to establish the constancy of nuclear decay rates. For example, Emery G.T. stated [2]: • ≪Early workers tried to change the decay constants of various members of the natural radioactive series by varying the temperature between 24◦K and 1280◦K, by applying pressure of up to 2000 atm, by taking sources down into mines and up to the Jungfraujoch, by applying magnetic fields of up to 83,000 Gauss, by whirling sources in centrifuges, and by many other ingenious techniques. Occasional positive results were usually understood, arXiv:nucl-th/0505021v1 8 May 2005 in time, as result of changes in the counting geometry, or of the loss of volatile members of the natural decay chains.
    [Show full text]
  • Modern Physics to Which He Did This Observation, Usually to Within About 0.1%
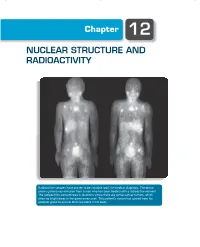
    Chapter 12 NUCLEAR STRUCTURE AND RADIOACTIVITY Radioactive isotopes have proven to be valuable tools for medical diagnosis. The photo shows gamma-ray emission from a man who has been treated with a radioactive element. The radioactivity concentrates in locations where there are active cancer tumors, which show as bright areas in the gamma-ray scan. This patient’s cancer has spread from his prostate gland to several other locations in his body. 370 Chapter 12 | Nuclear Structure and Radioactivity The nucleus lies at the center of the atom, occupying only 10−15 of its volume but providing the electrical force that holds the atom together. Within the nucleus there are Z positive charges. To keep these charges from flying apart, the nuclear force must supply an attraction that overcomes their electrical repulsion. This nuclear force is the strongest of the known forces; it provides nuclear binding energies that are millions of times stronger than atomic binding energies. There are many similarities between atomic structure and nuclear structure, which will make our study of the properties of the nucleus somewhat easier. Nuclei are subject to the laws of quantum physics. They have ground and excited states and emit photons in transitions between the excited states. Just like atomic states, nuclear states can be labeled by their angular momentum. There are, however, two major differences between the study of atomic and nuclear properties. In atomic physics, the electrons experience the force provided by an external agent, the nucleus; in nuclear physics, there is no such external agent. In contrast to atomic physics, in which we can often consider the interactions among the electrons as a perturbation to the primary interaction between electrons and nucleus, in nuclear physics the mutual interaction of the nuclear constituents is just what provides the nuclear force, so we cannot treat this complicated many- body problem as a correction to a single-body problem.
    [Show full text]
  • Β-Particle Energy-Summing Correction for Β-Delayed Proton Emission Measurements
    β-particle energy-summing correction for β-delayed proton emission measurements Z. Meisela,b,∗, M. del Santob,c, H.L. Crawfordd, R.H. Cyburtb,c, G.F. Grinyere, C. Langerb,f, F. Montesb,c, H. Schatzb,c,g, K. Smithb,h aInstitute of Nuclear and Particle Physics, Department of Physics and Astronomy, Ohio University, Athens, OH 45701, USA bJoint Institute for Nuclear Astrophysics { Center for the Evolution of the Elements, www.jinaweb.org cNational Superconducting Cyclotron Laboratory, Michigan State University, East Lansing, MI 48824, USA dNuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA eGrand Acc´el´erateur National d'Ions Lourds, CEA/DSM-CNRS/IN2P3, Caen 14076, France fInstitute for Applied Physics, Goethe University Frankfurt am Main, 60438 Frankfurt am Main, Germany gDepartment of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA hDepartment of Physics and Astronomy, University of Tennessee, Knoxville, TN 37996, USA Abstract A common approach to studying β-delayed proton emission is to measure the energy of the emitted proton and corresponding nuclear recoil in a double-sided silicon-strip detector (DSSD) after implanting the β-delayed proton- emitting (βp) nucleus. However, in order to extract the proton-decay energy from the total decay energy which is measured, the decay (proton + recoil) energy must be corrected for the additional energy implanted in the DSSD by the β-particle emitted from the βp nucleus, an effect referred to here as β-summing. We present an approach to determine an accurate correction for β-summing. Our method relies on the determination of the mean implantation depth of the βp nucleus within the DSSD by analyzing the shape of the total (proton + recoil + β) decay energy distribution shape.
    [Show full text]
  • R-Process Nucleosynthesis: on the Astrophysical Conditions
    r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalischer Modelle Zur Erlangung des Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim Tag der Einreichung: 07.02.2017, Tag der Prüfung: 29.05.2017 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Fachbereich Physik Institut für Kernphysik Theoretische Astrophysik r-process nucleosynthesis: on the astrophysical conditions and the impact of nuclear physics input r-Prozess Nukleosynthese: Über die astrophysikalischen Bedingungen und den Einfluss kernphysikalis- cher Modelle Genehmigte Dissertation von M.Sc. Dirk Martin, geb. in Rüsselsheim 1. Gutachten: Prof. Dr. Almudena Arcones Segovia 2. Gutachten: Prof. Dr. Jochen Wambach Tag der Einreichung: 07.02.2017 Tag der Prüfung: 29.05.2017 Darmstadt 2017 — D 17 Bitte zitieren Sie dieses Dokument als: URN: urn:nbn:de:tuda-tuprints-63017 URL: http://tuprints.ulb.tu-darmstadt.de/6301 Dieses Dokument wird bereitgestellt von tuprints, E-Publishing-Service der TU Darmstadt http://tuprints.ulb.tu-darmstadt.de [email protected] Die Veröffentlichung steht unter folgender Creative Commons Lizenz: Namensnennung – Keine kommerzielle Nutzung – Keine Bearbeitung 4.0 International https://creativecommons.org/licenses/by-nc-nd/4.0/ Für meine Uroma Helene. Abstract The origin of the heaviest elements in our Universe is an unresolved mystery. We know that half of the elements heavier than iron are created by the rapid neutron capture process (r-process). The r-process requires an ex- tremely neutron-rich environment as well as an explosive scenario.
    [Show full text]