Lecture20-Nov30
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
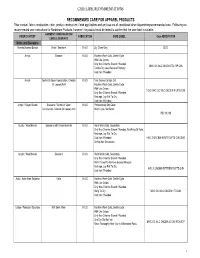
Care Label Recommendations
CARE LABEL RECOMMENDATIONS RECOMMENDED CARE FOR APPAREL PRODUCTS Fiber content, fabric construction, color, product construction, finish applications and end use are all considered when determining recommended care. Following are recommended care instructions for Nordstrom Products, however; the product must be tested to confirm that the care label is suitable. GARMENT/ CONSTRUCTION/ FIBER CONTENT FABRICATION CARE LABEL Care ABREVIATION EMBELLISHMENTS Knits and Sweaters Acetate/Acetate Blends Knits / Sweaters K & S Dry Clean Only DCO Acrylic Sweater K & S Machine Wash Cold, Gentle Cycle With Like Colors Only Non-Chlorine Bleach If Needed MWC GC WLC ONCBIN TDL RP CIIN Tumble Dry Low, Remove Promptly Cool Iron If Needed Acrylic Gentle Or Open Construction, Chenille K & S Turn Garment Inside Out Or Loosely Knit Machine Wash Cold, Gentle Cycle With Like Colors TGIO MWC GC WLC ONCBIN R LFTD CIIN Only Non-Chlorine Bleach If Needed Reshape, Lay Flat To Dry Cool Iron If Needed Acrylic / Rayon Blends Sweaters / Gentle Or Open K & S Professionally Dry Clean Construction, Chenille Or Loosely Knit Short Cycle, No Steam PDC SC NS Acrylic / Wool Blends Sweaters with Embelishments K & S Hand Wash Cold, Separately Only Non-Chlorine Bleach If Needed, No Wring Or Twist Reshape, Lay Flat To Dry Cool Iron If Needed HWC S ONCBIN NWOT R LFTD CIIN DNID Do Not Iron Decoration Acrylic / Wool Blends Sweaters K & S Hand Wash Cold, Separately Only Non-Chlorine Bleach If Needed Roll In Towel To Remove Excess Moisture Reshape, Lay Flat To Dry HWC S ONCBIN RITTREM -

Choosing the Proper Short Cut Fiber for Your Nonwoven Web
Choosing The Proper Short Cut Fiber for Your Nonwoven Web ABSTRACT You have decided that your web needs a synthetic fiber. There are three important factors that have to be considered: generic type, diameter, and length. In order to make the right choice, it is important to know the chemical and physical characteristics of the numerous man-made fibers, and to understand what is meant by terms such as denier and denier per filament (dpf). PROPERTIES Denier Denier is a property that varies depending on the fiber type. It is defined as the weight in grams of 9,000 meters of fiber. The current standard of denier is 0.05 grams per 450 meters. Yarn is usually made up of numerous filaments. The denier of the yarn divided by its number of filaments is the denier per filament (dpf). Thus, denier per filament is a method of expressing the diameter of a fiber. Obviously, the smaller the denier per filament, the more filaments there are in the yarn. If a fairly closed, tight web is desired, then lower dpf fibers (1.5 or 3.0) are preferred. On the other hand, if high porosity is desired in the web, a larger dpf fiber - perhaps 6.0 or 12.0 - should be chosen. Here are the formulas for converting denier into microns, mils, or decitex: Diameter in microns = 11.89 x (denier / density in grams per milliliter)½ Diameter in mils = diameter in microns x .03937 Decitex = denier x 1.1 The following chart may be helpful. Our stock fibers are listed along with their density and the diameter in denier, micron, mils, and decitex for each: Diameter Generic Type -

Investigation of the Mechanical Properties of a Carbon Fibre-Reinforced Nylon Filament for 3D Printing
machines Article Investigation of the Mechanical Properties of a Carbon Fibre-Reinforced Nylon Filament for 3D Printing Flaviana Calignano 1,* , Massimo Lorusso 2 , Ignanio Roppolo 3 and Paolo Minetola 1 1 Department of Management and Production Engineering, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Turin, Italy; [email protected] 2 Istituto Italiano di Tecnologia, Center for Sustainable Future Technologies IIT@Polito, Corso Trento 21, 10129 Turin, Italy; [email protected] 3 Department of Applied Science and Technology, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Turin, Italy; [email protected] * Correspondence: fl[email protected]; Tel.: +39-011-090-7218 Received: 19 July 2020; Accepted: 2 September 2020; Published: 4 September 2020 Abstract: Additive manufacturing (i.e., 3D printing) has rapidly developed in recent years. In the recent past, many researchers have highlighted the development of in-house filaments for fused filament fabrication (FFF), which can extend the corresponding field of application. Due to the limited mechanical properties and deficient functionality of printed polymer parts, there is a need to develop printable polymer composites that exhibit high performance. This study analyses the actual mechanical characteristics of parts fabricated with a low-cost printer from a carbon fibre-reinforced nylon filament. The results show that the obtained values differ considerably from the values presented in the datasheets of various filament suppliers. Moreover, the hardness and tensile strength are influenced by the building direction, the infill percentage, and the thermal stresses, whereas the resilience is affected only by the building direction. Furthermore, the relationship between the mechanical properties and the filling factor is not linear. -

Analysis of the Polyester Clothing Value Chain to Identify Key Intervention Points for Sustainability Cristina Palacios‑Mateo* , Yvonne Van Der Meer and Gunnar Seide
Palacios‑Mateo et al. Environ Sci Eur (2021) 33:2 https://doi.org/10.1186/s12302‑020‑00447‑x REVIEW Open Access Analysis of the polyester clothing value chain to identify key intervention points for sustainability Cristina Palacios‑Mateo* , Yvonne van der Meer and Gunnar Seide Abstract Clothing is one of the primary human needs, and the demand is met by the global production of thousands of tons of textile fbers, fabrics and garments every day. Polyester clothing manufactured from oil‑based polyethylene tereph‑ thalate (PET) is the market leader. Conventional PET creates pollution along its entire value chain—during the produc‑ tion, use and end‑of‑life phases—and also contributes to the unsustainable depletion of resources. The consumption of PET garments thus compromises the quality of land, water and air, destroys ecosystems, and endangers human health. In this article, we discuss the diferent stages of the value chain for polyester clothing from the perspective of sustainability, describing current environmental challenges such as pollution from textile factory wastewater, and microfbers released from clothing during the laundry cycle. We also consider potential solutions such as enhanced reuse and recycling. Finally, we propose a series of recommendations that should be applied to polyester clothing at all stages along the value chain, ofering the potential for meaningful and efective change to improve the environ‑ mental sustainability of polyester textiles on a global scale. Keywords: PET, Textiles, Value chain, Environmental sustainability, Microfbers, Pollution, Recycling, Life cycle Introduction with 2019 estimates in Germany suggesting an average Te global volume of fber production for textile manu- lifetime of only 4.4 years [5]. -

DID YOU KNOW? PET (Polyethylene Terephthalate) Is Actually Polyester. When PET Is Used for Bottles, Containers and Other
355 Lexington Ave., Suite 1500 ▪ New York, NY 10017 ▪ www.PETresin.org DID YOU KNOW? Little-Known Facts about PET Plastic . PET (polyethylene terephthalate) is actually polyester. When PET is used for bottles, containers and other applications, it is called PET or PET resin. When PET is used as a fiber, it is typically called polyester. The PET bottle was invented by Nathaniel C. Wyeth, a DuPont engineer and brother of American painter Andrew Wyeth. The patent was issued to Wyeth in 1973 and assigned to DuPont. According to the EPA, recycling one pound of PET bottles (that’s about 10 two-liter soda bottles) saves approximately 26,000 BTUs of energy. PET bottles and the sun are helping millions of people in developing countries obtain potable water. Using a system called SODIS (solar water disinfection), inhabitants set water-filled PET bottles in the sun for several hours or days – depending on how much sunlight is available – as a simple but effective means of destroying disease-causing bacteria and gaining safe drinking water. More than 1.5 billion pounds of used PET bottles and containers are collected in the U.S. each year for recycling. PET is the most recycled plastic in the U.S. and the world. A single-serve PET bottle (0.5 liter) is strong enough to hold 50 times its weight in water. Chemists keep finding new ways to make PET lighter without losing any strength. A 2-liter PET bottle that weighed 68 grams in 1980 now weighs as little as 42 grams. The average weight of single-serve 0.5 liter PET water bottle is now 9.9 grams, nearly half of what it weighed in 2000. -

Natural Fibers and Fiber-Based Materials in Biorefineries
Natural Fibers and Fiber-based Materials in Biorefineries Status Report 2018 This report was issued on behalf of IEA Bioenergy Task 42. It provides an overview of various fiber sources, their properties and their relevance in biorefineries. Their status in the scientific literature and market aspects are discussed. The report provides information for a broader audience about opportunities to sustainably add value to biorefineries by considerin g fiber applications as possible alternatives to other usage paths. IEA Bioenergy Task 42: December 2018 Natural Fibers and Fiber-based Materials in Biorefineries Status Report 2018 Report prepared by Julia Wenger, Tobias Stern, Josef-Peter Schöggl (University of Graz), René van Ree (Wageningen Food and Bio-based Research), Ugo De Corato, Isabella De Bari (ENEA), Geoff Bell (Microbiogen Australia Pty Ltd.), Heinz Stichnothe (Thünen Institute) With input from Jan van Dam, Martien van den Oever (Wageningen Food and Bio-based Research), Julia Graf (University of Graz), Henning Jørgensen (University of Copenhagen), Karin Fackler (Lenzing AG), Nicoletta Ravasio (CNR-ISTM), Michael Mandl (tbw research GesmbH), Borislava Kostova (formerly: U.S. Department of Energy) and many NTLs of IEA Bioenergy Task 42 in various discussions Disclaimer Whilst the information in this publication is derived from reliable sources, and reasonable care has been taken in its compilation, IEA Bioenergy, its Task42 Biorefinery and the authors of the publication cannot make any representation of warranty, expressed or implied, regarding the verity, accuracy, adequacy, or completeness of the information contained herein. IEA Bioenergy, its Task42 Biorefinery and the authors do not accept any liability towards the readers and users of the publication for any inaccuracy, error, or omission, regardless of the cause, or any damages resulting therefrom. -

Handle and Comfort Characteristics of Cotton Core Spun Lycra and Polyester/ Lycra Fabrics for Application As Blouse Nirmala Varghese and G
Volume 8, Issue 4, Spring2014 Handle and Comfort Characteristics of Cotton Core Spun Lycra and Polyester/ Lycra Fabrics for Application as Blouse Nirmala Varghese and G. Thilagavathi Department of Apparel & Fashion Technology PSG College of Technology Tamil Nadu, India ABSTRACT Stretchable plain woven fabrics are developed with 60s cotton core spun Lycra and polyester Lycra twisted yarn (91D) in weft with cotton, silk and polyester in warp. The influence of fabric specifications on thermal comfort, low stress mechanical properties, primary and total hand value is analyzed. The results indicated that cotton core spun Lycra woven with polyester warp provided higher value of thermal conductivity, air permeability and water vapor permeability. The woven stretch fabrics produced with polyester warp, cotton core spun Lycra and polyester Lycra in weft has excellent aesthetic and drape properties. These fabrics have higher tensile resilience, tensile strain, lower shear rigidity, superior primary hand and a higher total hand value of 4.08 and 3.93 respectively and are best suitable for women’s blouse. Keywords: Cotton core spun Lycra, polyester/Lycra, woven stretch, fabric handle, sari blouse Introduction Lycra and polyester/lycra twisted yarn. Several studies have been carried out Stretch is often the most important investigating the physical properties of core property of textiles that contribute to wearer spun yarn, cotton/lycra and properties of the comfort. The stretch yarn and fabrics are fabrics containing different rates of spandex widely used and preferred by the people in yarns. Core spun cotton/spandex shows high the last few years all over the world because resiliency property than 100% cotton yarns, of their stretch ability and shape retention due to its soft and rubbery isocyanate properties. -
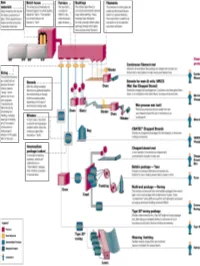
All About Fibers
RawRaw MaterialsMaterials ¾ More than half the mix is silica sand, the basic building block of any glass. ¾ Other ingredients are borates and trace amounts of specialty chemicals. Return © 2003, P. Joyce BatchBatch HouseHouse && FurnaceFurnace ¾ The materials are blended together in a bulk quantity, called the "batch." ¾ The blended mix is then fed into the furnace or "tank." ¾ The temperature is so high that the sand and other ingredients dissolve into molten glass. Return © 2003, P. Joyce BushingsBushings ¾The molten glass flows to numerous high heat-resistant platinum trays which have thousands of small, precisely drilled tubular openings, called "bushings." Return © 2003, P. Joyce FilamentsFilaments ¾This thin stream of molten glass is pulled and attenuated (drawn down) to a precise diameter, then quenched or cooled by air and water to fix this diameter and create a filament. Return © 2003, P. Joyce SizingSizing ¾The hair-like filaments are coated with an aqueous chemical mixture called a "sizing," which serves two main purposes: 1) protecting the filaments from each other during processing and handling, and 2) ensuring good adhesion of the glass fiber to the resin. Return © 2003, P. Joyce WindersWinders ¾ In most cases, the strand is wound onto high-speed winders which collect the continuous fiber glass into balls or "doffs.“ Single end roving ¾ Most of these packages are shipped directly to customers for such processes as pultrusion and filament winding. ¾ Doffs are heated in an oven to dry the chemical sizing. Return © 2003, P. Joyce IntermediateIntermediate PackagePackage ¾ In one type of winding operation, strands are collected into an "intermediate" package that is further processed in one of several ways. -

Carbon Fiber Supply and Demand
Carbon Fiber Supply and Demand Supply of PAN based carbon fiber New players could make all the difference San Diego, California, USA October 23 2007 The ongoing shortage of PAN based carbon fibers has seen the planning, development and realization of new carbon fiber manufacturing capacity in new countries. The start up of new plant faces many hurdles, especially in the face of competition that has been in the business for many decades. However these hurdles have been overcome and this process will enable carbon fiber to become truly a commodity product, available to the vast range of current and new composite applications. Latest News (Press releases in the last 4 weeks) Supply October 11, 2007 Capacity Expansion of Carbon Fiber “TENAX®” Toho Tenax Co., Ltd. (Head Office: Bunkyo-ku, Tokyo, President: Yoshikuni Utsunomiya), which is engaged in the business of carbon fibers within the Teijin Group, has decided to add a new carbon fiber production line at Toho Tenax Europe GmbH (located at Wuppertal, Germany. October 05, 2007 SGL Group plans to triple carbon fiber capacities SGL Group plans to triple carbon fiber capacities Capacity increase up to 12,000 metric tons by 2012 Demand September 27, 2007 British Airways Green light for aircraft orders British Airways has today placed an order for 12 Airbus A380 and 24 Boeing 787 aircraft with options for a further seven Airbus A380s and18 Boeing 787s. The British Airways Order The new aircraft will replace 34 of the airline's long haul fleet and will be delivered between 2010 and 2014. The order, including options, will give the airline the ability to grow its capacity by up to four per cent per year and the flexibility to tailor its future capacity growth in line with market conditions. -
Natural Fiber Composites for Space Applications
Natural fiber composites for space applications Clean Space industrial days, 25.10.2017 Julien Rion, CTO Bcomp Ltd 1700 Fribourg Switzerland ABOUT BCOMP . Founded 2011, 12 Employees . Several innovation- and start-up awards, including Swiss Economic Award 2016 . Broad customer basis in Sports & Leisure and Luxury industries (e.g. K2, Black Diamond, Nordica, Stöckli, Starboard) . Lightweighting development projects with leading Automotive OEMs . International academic/research network 07.11.2017 2 OUR VALUE PROPOSITION We deliver lightweight, high-performance materials in a renewable package . Weight reduction of up to 40% . Material cost reduction of up to 30% Flax fibres Structural part Bcomp reinforcement 07.11.2017 3 BCOMP PRODUCT PORTFOLIO bCores® ampliTex® powerRibs Services 07.11.2017 4 Why using natural fibers? . High specific stiffness . Good vibration damping properties . Probably demisable . Radio-transparent . Sustainable fibers State of the art for space applications Are natural fibers applicable for space? . Tensiles tests between -50 and 150°C . DMA tests from -150°C to 150°C . TMA tests . Outgasing tests . Moisture tests Tensile tests . High specific stiffness at low temperature . Bilinear behaviour . Loss of stiffness with temperature increase Stiffness 48 12 E1 44 11 E2 40 ET 10 36 9 32 8 28 7 24 6 20 5 16 4 [GPa] ET E1 , E2 [GPa] E1 , 12 3 8 2 4 1 0 0 -100 -50 0 50 100 150 200 T [°C] DMA tests Test on L specimens: . Constant decrease of E with T increase . Damping quite constant DMA tests 80 E-modulus: 70 . Constant decrease of E 60 with T increase 50 40 . -

Basic of Textiles
BASIC OF TEXTILES BFA(F) 202 CC 5 Directorate of Distance Education SWAMI VIVEKANAND SUBHARTI UNIVERSITY MEERUT 250005 UTTAR PRADESH SIM MOUDLE DEVELOPED BY: Reviewed by the study Material Assessment Committed Comprising: 1. Dr. N.K.Ahuja, Vice Chancellor Copyright © Publishers Grid No part of this publication which is material protected by this copyright notice may be reproduce or transmitted or utilized or store in any form or by any means now know or here in after invented, electronic, digital or mechanical. Including, photocopying, scanning, recording or by any informa- tion storage or retrieval system, without prior permission from the publisher. Information contained in this book has been published by Publishers Grid and Publishers. and has been obtained by its author from sources believed to be reliable and are correct to the best of their knowledge. However, the publisher and author shall in no event be liable for any errors, omission or damages arising out of this information and specially disclaim and implied warranties or merchantability or fitness for any particular use. Published by: Publishers Grid 4857/24, Ansari Road, Darya ganj, New Delhi-110002. Tel: 9899459633, 7982859204 E-mail: [email protected], [email protected] Printed by: A3 Digital Press Edition : 2021 CONTENTS 1. Fiber Study 5-64 2. Fiber and its Classification 65-175 3. Yarn and its Types 176-213 4. Fabric Manufacturing Techniques 214-260 5. Knitted 261-302 UNIT Fiber Study 1 NOTES FIBER STUDY STRUCTURE 1.1 Learning Objective 1.2 Introduction 1.3 Monomer, Polymer, Degree of polymerization 1.4 Student Activity 1.5 Properties of Fiber: Primary & Secondary 1.6 Summary 1.7 Glossary 1.8 Review Questions 1.1 LEARNING OBJECTIVE After studying this unit you should be able to: ● Describe the Natural Fiber. -

Blending Cotton and Polyester Fibers
BLENDING COTTON AND POLYESTER FIBERS-- EFFECTS OF PROCESSING METHODS ON FIBER DISTRIBUTION AND YARN PROPERTIES A THESIS Presented to The Faculty of the Graduate Division by Nelson Ping Ching Chao In Partial Fulfillment of the Requirements for the Degree Master of Science in Textiles Georgia Institute of Technology September, 1963 3^ 12,^ ^ BLENDING COTTON AND POLYESTER FIBERS- EFFECTS OF PROCESSING METHODS ON FIBER DISTRIBUTION AND YARN PROPERTIES Approved! "—xy '—17 Date Approved by Chairman: ^^ysu^.^1^ ^h^ R^^ li ACKNOWLEDGMENTS The author wishes to express his sincere gratitude and apprecia tion to Dr. James L. Taylor, Director of the A. French Textile School, £or granting him a graduate assistantship and a Celanese fellowship which made this study possible; to Professor R. K. Flege, his thesis advisor, and to Professor R. L. Hill, both of the A. French Textile School, for their advice and recommendations; and to Dr. Joseph J. Moder of the School of Industrial Engineering for his assistance with the statistical aspects of the experiment. He also extends his thanks to Mr. R. C. Freeman, technician of the A. French Textile School, for his kind assistance. iii TABLE OF CONTENTS Page ACKNOWLEDGMENTS ii LIST OF TABLES iv LIST OF ILLUSTRATIONS vii SUMMARY vill Chapter I. INTRODUCTION I Some Aspects of Blending Fibers Stateioent of the Problem II. INSTRUMENTATION AND EQUIPMENT 11 Raw Materials Used Processing Equipment Testing Equipment III. PROCEDURE 13 Processing Blended Yarn Physical Tests Tests for Uniformity Tests for Breaking Strength and Elongation of Yarn Examination of Fiber Distribution Analyses of Data IV. DISCUSSION OF RESULTS 24 V.