DOCSLIB.ORG

Lunar Orbiter State Estimation Using Neural Network-Based Crater

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lunar Orbiter State Estimation Using Neural Network-Based Crater Lunar Orbiter State Estimation Using Neural Network-based Crater Detection by Lena Downes B.S., University of New Hampshire (2018) Submitted to the Department of Aeronautics and Astronautics in partial fulfillment of the requirements for the degree of Master of Science in Aeronautics and Astronautics at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY May 2020 ○c Massachusetts Institute of Technology 2020. All rights reserved. Author................................................................ Department of Aeronautics and Astronautics May 19, 2020 Certified by. Jonathan P. How Richard C. Maclaurin Professor of Aeronautics and Astronautics, MIT Thesis Supervisor Certified by. Theodore J. Steiner Senior Member of the Technical Staff, Draper Thesis Supervisor Accepted by . Sertac Karaman Associate Professor of Aeronautics and Astronautics, MIT Chair, Graduate Program Committee 2 Lunar Orbiter State Estimation Using Neural Network-based Crater Detection by Lena Downes Submitted to the Department of Aeronautics and Astronautics on May 19, 2020, in partial fulfillment of the requirements for the degree of Master of Science in Aeronautics and Astronautics Abstract Terrain relative navigation can improve the precision of a spacecraft’s state estimate by providing supplementary measurements to correct for drift in the inertial naviga- tion system. This thesis presents a crater detector, LunaNet, that uses a convolutional neural network and image processing methods to detect craters from imagery taken by a spacecraft’s on-board camera. These detections are matched with known lu- nar craters, and these matches can be used as features that are input to a extended Kalman filter. Our results show that, on average, LunaNet detects approximately twice the number of craters in an intensity image as two other successful intensity image-based crater detectors, and detects more accurate crater centers and diameters than the other two detectors as well. One of the challenges of using cameras for this task is that they can generate imagery with differences in image qualities and noise levels. These differences can occur for reasons such as changes in irradiance ofthe lunar surface, heating of camera electronic elements, or the inherent fluctuation of discrete photons. These image noise effects are difficult to compensate for, makingit important for a crater detector to be robust to noise. When trained on diverse data, convolutional neural networks are able to generalize over varied imagery. Similarly, LunaNet is shown to be robust to four types of image manipulation that result in changes to image qualities and noise levels of the input imagery. LunaNet also pro- duces more repeatable crater detections from frame to frame throughout a trajectory, and that enables more reliable state estimation over a trajectory. A LunaNet-based EKF experiences fewer spikes in estimation error and has lower average estimation error than EKFs using other successful crater detectors. Thesis Supervisor: Jonathan P. How Title: Richard C. Maclaurin Professor of Aeronautics and Astronautics, MIT Thesis Supervisor: Theodore J. Steiner Title: Senior Member of the Technical Staff, Draper 3 4 Acknowledgments I would like to thank my advisors, Professor Jonathan How of MIT and Ted Steiner of Draper. I have learned immensely from all of the careful guidance and instruction that I have received from you both. Ted, your generosity with your time both to help me work through technical problems and to be a welcoming ear when I needed more general support has been truly appreciated. Your advice, from which classes to take to what direction to develop my career towards, has given me structure and clarity and has helped me to grow into the researcher that I am becoming. Jon, your sharp eye and deep knowledge of the field have molded my technical capabilities and honed my ability to focus on the important questions. You have pushed me harder than I have ever been pushed, and as a result I have achieved more than I ever thought that I could within these two years. I am extremely grateful to Draper in their support of my work. Four years ago I heard about Draper and the Draper Fellowship program, and I set my sights on it. Draper gave me a chance by offering me a software engineering internship when I was an undergraduate mechanical engineering student who did not want to be a mechanical engineer. In that internship I found my passion in visual navigation. I do not believe that I would be where I am today without that internship and the subsequent guidance and support of Draper, and for that I cannot thank Draper enough. Thank you to my family and friends, many of whom could not verbalize what I research beyond “landing on the Moon,” but who have been so incredibly supportive and have endured far too many impromptu technical talks on my part. To my parents and siblings, who have never questioned my decision or my ability to pursue an advanced degree, I am so grateful. Thinking deeply, questioning things, and reading have always been encouraged in our home, and a childhood surrounded by books has prepared me for a life of learning. To my friends, for commiserating, sharing in the struggles, and lifting each other up, thank you. You have kept me mentally afloat and given my life balance. To Carl, who has listened to one million complaints and who 5 always strikes the perfect balance of listening, offering advice, and consoling, thank you. You have made these challenging years so much sweeter. I would like to acknowledge the support of Amazon Web Services, which enabled much of this research. Thank you for your generous donation of computational re- sources. 6 Contents 1 Introduction 13 1.1 Precise State Estimation . 13 1.2 Terrain Relative Navigation . 15 1.3 Crater Detection . 16 1.4 LunaNet . 17 2 Background and Related Work 21 2.1 Terrain Relative Navigation . 21 2.2 Crater Detection and Matching . 26 2.2.1 Crater Detection . 26 2.2.2 Machine Learning . 28 2.2.3 Deep Learning Crater Detection . 30 2.2.4 Crater Identification . 33 2.3 Summary . 34 3 Methods 37 3.1 Crater Detection with LunaNet . 38 3.1.1 LunaNet’s Neural Network Subsystem . 38 3.1.2 LunaNet’s Image Processing Subsystem . 44 3.2 Crater Identification . 47 3.3 Extended Kalman Filter . 51 3.3.1 State Space . 51 3.3.2 State Propagation . 52 7 3.3.3 Measurement Update . 54 3.3.4 Kalman Update . 55 3.4 Summary . 55 4 Results 57 4.1 Crater Detection . 58 4.2 Extended Kalman Filter . 70 4.2.1 LunaNet Precision and Accuracy Analysis . 70 4.2.2 LunaNet Detection over a Trajectory . 73 4.2.3 EKF Monte Carlo Simulations . 78 4.3 Summary . 86 5 Conclusion 87 8 List of Figures 3-1 LunaNet system overview. 38 3-2 DeepMoon training image sets. 40 3-3 Crater database overlaid on Moon. 41 3-4 LunaNet training image sets. 43 3-5 LunaNet prediction image processing. 46 3-6 Convex hull example. 48 3-7 RANSAC crater matching example. 49 3-8 Crater matching process. 50 4-1 Example comparison of crater detectors. 60 4-2 Comparison of LRO image with and without different kinds of noise. 62 4-3 Comparison of number of matched craters from different crater detectors. 65 4-4 Example comparison of crater detectors on bright images. 66 4-5 Comparison of accuracy of different crater detectors. 68 4-6 Comparison of detection speed of different crater detectors. 68 4-7 Normalized comparison of detection speed of different crater detectors. 69 4-8 LunaNet detection accuracy and precision. 71 4-9 Close-up of Fig. 4-8 . 71 4-10 Histogram of LunaNet detection accuracy and precision. 72 4-11 Close-up of Fig. 4-10 . 72 4-12 Example test trajectory. 74 4-13 Example test trajectory, overhead view. 74 4-14 Example image persistence of a crater detection. 76 9 4-15 Average image persistence over a trajectory. 77 4-16 Average number of craters detected over a trajectory. 78 4-17 EKF position error for different crater detectors. 79 4-18 EKF velocity error for different crater detectors. 80 4-19 Effect of crater matching on estimation error. 82 4-20 EKF state error for different crater detectors with noise. 83 4-21 Position plot of Fig. 4-20 separated by noise. 84 4-22 Close-up of position plot of Fig. 4-21. 85 10 List of Tables 3.1 Parameters Used to Train LunaNet with Intensity Images . 44 4.1 Crater Detector EKF Monte-Carlo Performance . 81 11 12 Chapter 1 Introduction 1.1 Precise State Estimation In the days of Apollo, the mission was challenging but straightforward: land a man on the Moon by the end of the 1960s. This meant that it was possible to fulfill the mission goals while landing in the safest, least hazardous location possible on the lunar surface. The future of lunar exploration and development expands upon these goals. The return to the Moon focuses not just on landing on its surface, but on finding ways to build infrastructure and extract resources from the Moon after wedo so. These new goals require higher precision navigation in order to enable safely and precisely landing on the Moon. Precision landing enables the mining of a resource, like water, on the Moon. The presence of frozen water was detected in craters around the lunar northern and south- ern poles by NASA’s Moon Mineralogy Mapper instrument, which flew aboard India’s Chandrayaan-1 spacecraft in 2018 [30]. Frozen water is a useful resource because it is possible to combine nano-scale aluminum with water and use it as rocket fuel [25]. This means that the Moon could serve as a refueling location for spacecraft to stop at on their way to deeper space destinations.
Load more

Recommended publications
  • No. 40. the System of Lunar Craters, Quadrant Ii Alice P
    NO. 40. THE SYSTEM OF LUNAR CRATERS, QUADRANT II by D. W. G. ARTHUR, ALICE P. AGNIERAY, RUTH A. HORVATH ,tl l C.A. WOOD AND C. R. CHAPMAN \_9 (_ /_) March 14, 1964 ABSTRACT The designation, diameter, position, central-peak information, and state of completeness arc listed for each discernible crater in the second lunar quadrant with a diameter exceeding 3.5 km. The catalog contains more than 2,000 items and is illustrated by a map in 11 sections. his Communication is the second part of The However, since we also have suppressed many Greek System of Lunar Craters, which is a catalog in letters used by these authorities, there was need for four parts of all craters recognizable with reasonable some care in the incorporation of new letters to certainty on photographs and having diameters avoid confusion. Accordingly, the Greek letters greater than 3.5 kilometers. Thus it is a continua- added by us are always different from those that tion of Comm. LPL No. 30 of September 1963. The have been suppressed. Observers who wish may use format is the same except for some minor changes the omitted symbols of Blagg and Miiller without to improve clarity and legibility. The information in fear of ambiguity. the text of Comm. LPL No. 30 therefore applies to The photographic coverage of the second quad- this Communication also. rant is by no means uniform in quality, and certain Some of the minor changes mentioned above phases are not well represented. Thus for small cra- have been introduced because of the particular ters in certain longitudes there are no good determi- nature of the second lunar quadrant, most of which nations of the diameters, and our values are little is covered by the dark areas Mare Imbrium and better than rough estimates.
    [Show full text]
  • Glossary Glossary
    Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts.
    [Show full text]
  • Planetary Surfaces
    Chapter 4 PLANETARY SURFACES 4.1 The Absence of Bedrock A striking and obvious observation is that at full Moon, the lunar surface is bright from limb to limb, with only limited darkening toward the edges. Since this effect is not consistent with the intensity of light reflected from a smooth sphere, pre-Apollo observers concluded that the upper surface was porous on a centimeter scale and had the properties of dust. The thickness of the dust layer was a critical question for landing on the surface. The general view was that a layer a few meters thick of rubble and dust from the meteorite bombardment covered the surface. Alternative views called for kilometer thicknesses of fine dust, filling the maria. The unmanned missions, notably Surveyor, resolved questions about the nature and bearing strength of the surface. However, a somewhat surprising feature of the lunar surface was the completeness of the mantle or blanket of debris. Bedrock exposures are extremely rare, the occurrence in the wall of Hadley Rille (Fig. 6.6) being the only one which was observed closely during the Apollo missions. Fragments of rock excavated during meteorite impact are, of course, common, and provided both samples and evidence of co,mpetent rock layers at shallow levels in the mare basins. Freshly exposed surface material (e.g., bright rays from craters such as Tycho) darken with time due mainly to the production of glass during micro- meteorite impacts. Since some magnetic anomalies correlate with unusually bright regions, the solar wind bombardment (which is strongly deflected by the magnetic anomalies) may also be responsible for darkening the surface [I].
    [Show full text]
  • March 21–25, 2016
    FORTY-SEVENTH LUNAR AND PLANETARY SCIENCE CONFERENCE PROGRAM OF TECHNICAL SESSIONS MARCH 21–25, 2016 The Woodlands Waterway Marriott Hotel and Convention Center The Woodlands, Texas INSTITUTIONAL SUPPORT Universities Space Research Association Lunar and Planetary Institute National Aeronautics and Space Administration CONFERENCE CO-CHAIRS Stephen Mackwell, Lunar and Planetary Institute Eileen Stansbery, NASA Johnson Space Center PROGRAM COMMITTEE CHAIRS David Draper, NASA Johnson Space Center Walter Kiefer, Lunar and Planetary Institute PROGRAM COMMITTEE P. Doug Archer, NASA Johnson Space Center Nicolas LeCorvec, Lunar and Planetary Institute Katherine Bermingham, University of Maryland Yo Matsubara, Smithsonian Institute Janice Bishop, SETI and NASA Ames Research Center Francis McCubbin, NASA Johnson Space Center Jeremy Boyce, University of California, Los Angeles Andrew Needham, Carnegie Institution of Washington Lisa Danielson, NASA Johnson Space Center Lan-Anh Nguyen, NASA Johnson Space Center Deepak Dhingra, University of Idaho Paul Niles, NASA Johnson Space Center Stephen Elardo, Carnegie Institution of Washington Dorothy Oehler, NASA Johnson Space Center Marc Fries, NASA Johnson Space Center D. Alex Patthoff, Jet Propulsion Laboratory Cyrena Goodrich, Lunar and Planetary Institute Elizabeth Rampe, Aerodyne Industries, Jacobs JETS at John Gruener, NASA Johnson Space Center NASA Johnson Space Center Justin Hagerty, U.S. Geological Survey Carol Raymond, Jet Propulsion Laboratory Lindsay Hays, Jet Propulsion Laboratory Paul Schenk,
    [Show full text]
  • Testing Hypotheses for the Origin of Steep Slope of Lunar Size-Frequency Distribution for Small Craters
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Springer - Publisher Connector Earth Planets Space, 55, 39–51, 2003 Testing hypotheses for the origin of steep slope of lunar size-frequency distribution for small craters Noriyuki Namiki1 and Chikatoshi Honda2 1Department of Earth and Planetary Sciences, Kyushu University, Hakozaki 6-10-1, Higashi-ku, Fukuoka 812-8581, Japan 2The Institute of Space and Astronautical Science, Yoshinodai 3-1-1, Sagamihara 229-8510, Japan (Received June 13, 2001; Revised June 24, 2002; Accepted January 6, 2003) The crater size-frequency distribution of lunar maria is characterized by the change in slope of the population between 0.3 and 4 km in crater diameter. The origin of the steep segment in the distribution is not well understood. Nonetheless, craters smaller than a few km in diameter are widely used to estimate the crater retention age for areas so small that the number of larger craters is statistically insufficient. Future missions to the moon, which will obtain high resolution images, will provide a new, large data set of small craters. Thus it is important to review current hypotheses for their distributions before future missions are launched. We examine previous and new arguments and data bearing on the admixture of endogenic and secondary craters, horizontal heterogeneity of the substratum, and the size-frequency distribution of the primary production function. The endogenic crater and heterogeneous substratum hypotheses are seen to have little evidence in their favor, and can be eliminated. The primary production hypothesis fails to explain a wide variation of the size-frequency distribution of Apollo panoramic photographs.
    [Show full text]
  • The British Astronomical Association Handbook 2017
    THE HANDBOOK OF THE BRITISH ASTRONOMICAL ASSOCIATION 2017 2016 October ISSN 0068–130–X CONTENTS PREFACE . 2 HIGHLIGHTS FOR 2017 . 3 CALENDAR 2017 . 4 SKY DIARY . .. 5-6 SUN . 7-9 ECLIPSES . 10-15 APPEARANCE OF PLANETS . 16 VISIBILITY OF PLANETS . 17 RISING AND SETTING OF THE PLANETS IN LATITUDES 52°N AND 35°S . 18-19 PLANETS – EXPLANATION OF TABLES . 20 ELEMENTS OF PLANETARY ORBITS . 21 MERCURY . 22-23 VENUS . 24 EARTH . 25 MOON . 25 LUNAR LIBRATION . 26 MOONRISE AND MOONSET . 27-31 SUN’S SELENOGRAPHIC COLONGITUDE . 32 LUNAR OCCULTATIONS . 33-39 GRAZING LUNAR OCCULTATIONS . 40-41 MARS . 42-43 ASTEROIDS . 44 ASTEROID EPHEMERIDES . 45-50 ASTEROID OCCULTATIONS .. ... 51-53 ASTEROIDS: FAVOURABLE OBSERVING OPPORTUNITIES . 54-56 NEO CLOSE APPROACHES TO EARTH . 57 JUPITER . .. 58-62 SATELLITES OF JUPITER . .. 62-66 JUPITER ECLIPSES, OCCULTATIONS AND TRANSITS . 67-76 SATURN . 77-80 SATELLITES OF SATURN . 81-84 URANUS . 85 NEPTUNE . 86 TRANS–NEPTUNIAN & SCATTERED-DISK OBJECTS . 87 DWARF PLANETS . 88-91 COMETS . 92-96 METEOR DIARY . 97-99 VARIABLE STARS (RZ Cassiopeiae; Algol; λ Tauri) . 100-101 MIRA STARS . 102 VARIABLE STAR OF THE YEAR (T Cassiopeiæ) . .. 103-105 EPHEMERIDES OF VISUAL BINARY STARS . 106-107 BRIGHT STARS . 108 ACTIVE GALAXIES . 109 TIME . 110-111 ASTRONOMICAL AND PHYSICAL CONSTANTS . 112-113 INTERNET RESOURCES . 114-115 GREEK ALPHABET . 115 ACKNOWLEDGEMENTS / ERRATA . 116 Front Cover: Northern Lights - taken from Mount Storsteinen, near Tromsø, on 2007 February 14. A great effort taking a 13 second exposure in a wind chill of -21C (Pete Lawrence) British Astronomical Association HANDBOOK FOR 2017 NINETY–SIXTH YEAR OF PUBLICATION BURLINGTON HOUSE, PICCADILLY, LONDON, W1J 0DU Telephone 020 7734 4145 PREFACE Welcome to the 96th Handbook of the British Astronomical Association.
    [Show full text]
  • Compositional and Mineralogical Characteristics of Archimedes Crater Region Using Chandrayaan – 1 M3 Data
    50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 1040.pdf COMPOSITIONAL AND MINERALOGICAL CHARACTERISTICS OF ARCHIMEDES CRATER REGION USING CHANDRAYAAN – 1 M3 DATA. P. R. Kumaresan1 and J. Saravanavel2, 1Research Scholar, 2Assistant Professor, Department of Remote Sensing, Bharathidasan University, Tiruchirappalli-23, Tamil Nadu, India, email: [email protected], [email protected] Introduction: The Earth’s natural satellite the tometry corrected reflectance data captured during the moon is nearest celestial body appears brightest object OP1B optical period. in our night sky. Moon surfaces are composed of dark and light areas. The dark areas are called Maria which is made up of basaltic terrain and light areas are high- lands mostly made up of Anorthositic rocks. The moon surface is littered with craters, which are formed when meteors hit its surface. To understand the evolution, geological process of the moon it is important to study the surface composition and minerals present in crustal surface. In this regard, in our study, we have attempted to map the minerals and surface composition of Archi- medes crater region. Study area: Archimedes crater is a large impact crater located on the eastern edges of the Mare Imbri- um of near side moon (29.7° N, 4.0° W). The diameter of the crater is 83 km with smooth floor flooded (1) with mare basalt and lack of a central peak. The rim (2) has a significant outer rampart brightened with ejecta (3) and the some portion of a terraced inner wall. Ar- chimedes Crater is named for the Greek mathematician Archimedes, who made many mathematical discoveries in the 200 B.C [1, 2].
    [Show full text]
  • The Moon After Apollo
    ICARUS 25, 495-537 (1975) The Moon after Apollo PAROUK EL-BAZ National Air and Space Museum, Smithsonian Institution, Washington, D.G- 20560 Received September 17, 1974 The Apollo missions have gradually increased our knowledge of the Moon's chemistry, age, and mode of formation of its surface features and materials. Apollo 11 and 12 landings proved that mare materials are volcanic rocks that were derived from deep-seated basaltic melts about 3.7 and 3.2 billion years ago, respec- tively. Later missions provided additional information on lunar mare basalts as well as the older, anorthositic, highland rocks. Data on the chemical make-up of returned samples were extended to larger areas of the Moon by orbiting geo- chemical experiments. These have also mapped inhomogeneities in lunar surface chemistry, including radioactive anomalies on both the near and far sides. Lunar samples and photographs indicate that the moon is a well-preserved museum of ancient impact scars. The crust of the Moon, which was formed about 4.6 billion years ago, was subjected to intensive metamorphism by large impacts. Although bombardment continues to the present day, the rate and size of impact- ing bodies were much greater in the first 0.7 billion years of the Moon's history. The last of the large, circular, multiringed basins occurred about 3.9 billion years ago. These basins, many of which show positive gravity anomalies (mascons), were flooded by volcanic basalts during a period of at least 600 million years. In addition to filling the circular basins, more so on the near side than on the far side, the basalts also covered lowlands and circum-basin troughs.
    [Show full text]
  • Water on the Moon, III. Volatiles & Activity
    Water on The Moon, III. Volatiles & Activity Arlin Crotts (Columbia University) For centuries some scientists have argued that there is activity on the Moon (or water, as recounted in Parts I & II), while others have thought the Moon is simply a dead, inactive world. [1] The question comes in several forms: is there a detectable atmosphere? Does the surface of the Moon change? What causes interior seismic activity? From a more modern viewpoint, we now know that as much carbon monoxide as water was excavated during the LCROSS impact, as detailed in Part I, and a comparable amount of other volatiles were found. At one time the Moon outgassed prodigious amounts of water and hydrogen in volcanic fire fountains, but released similar amounts of volatile sulfur (or SO2), and presumably large amounts of carbon dioxide or monoxide, if theory is to be believed. So water on the Moon is associated with other gases. Astronomers have agreed for centuries that there is no firm evidence for “weather” on the Moon visible from Earth, and little evidence of thick atmosphere. [2] How would one detect the Moon’s atmosphere from Earth? An obvious means is atmospheric refraction. As you watch the Sun set, its image is displaced by Earth’s atmospheric refraction at the horizon from the position it would have if there were no atmosphere, by roughly 0.6 degree (a bit more than the Sun’s angular diameter). On the Moon, any atmosphere would cause an analogous effect for a star passing behind the Moon during an occultation (multiplied by two since the light travels both into and out of the lunar atmosphere).
    [Show full text]
  • Appendix I Lunar and Martian Nomenclature
    APPENDIX I LUNAR AND MARTIAN NOMENCLATURE LUNAR AND MARTIAN NOMENCLATURE A large number of names of craters and other features on the Moon and Mars, were accepted by the IAU General Assemblies X (Moscow, 1958), XI (Berkeley, 1961), XII (Hamburg, 1964), XIV (Brighton, 1970), and XV (Sydney, 1973). The names were suggested by the appropriate IAU Commissions (16 and 17). In particular the Lunar names accepted at the XIVth and XVth General Assemblies were recommended by the 'Working Group on Lunar Nomenclature' under the Chairmanship of Dr D. H. Menzel. The Martian names were suggested by the 'Working Group on Martian Nomenclature' under the Chairmanship of Dr G. de Vaucouleurs. At the XVth General Assembly a new 'Working Group on Planetary System Nomenclature' was formed (Chairman: Dr P. M. Millman) comprising various Task Groups, one for each particular subject. For further references see: [AU Trans. X, 259-263, 1960; XIB, 236-238, 1962; Xlffi, 203-204, 1966; xnffi, 99-105, 1968; XIVB, 63, 129, 139, 1971; Space Sci. Rev. 12, 136-186, 1971. Because at the recent General Assemblies some small changes, or corrections, were made, the complete list of Lunar and Martian Topographic Features is published here. Table 1 Lunar Craters Abbe 58S,174E Balboa 19N,83W Abbot 6N,55E Baldet 54S, 151W Abel 34S,85E Balmer 20S,70E Abul Wafa 2N,ll7E Banachiewicz 5N,80E Adams 32S,69E Banting 26N,16E Aitken 17S,173E Barbier 248, 158E AI-Biruni 18N,93E Barnard 30S,86E Alden 24S, lllE Barringer 29S,151W Aldrin I.4N,22.1E Bartels 24N,90W Alekhin 68S,131W Becquerei
    [Show full text]
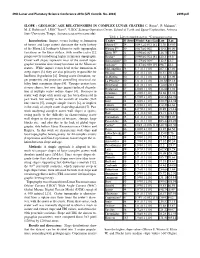
  • Slope - Geologic Age Relationships in Complex Lunar Craters C
    49th Lunar and Planetary Science Conference 2018 (LPI Contrib. No. 2083) 2399.pdf SLOPE - GEOLOGIC AGE RELATIONSHIPS IN COMPLEX LUNAR CRATERS C. Rojas1, P. Mahanti1, M. S. Robinson1, LROC Team1, 1LROC Science Operation Center, School of Earth and Space Exploration, Arizona State University, Tempe, Arizona ([email protected]) Table 1: List of complex craters. *Copernican craters Introduction: Impact events leading to formation Crater D (km) Model Age (Ga) Lon Lat of basins and large craters dominate the early history Moore F* 24 0.041∓0.012 [8] 37.30 185.0 of the Moon [1] leading to kilometer scale topographic Wiener F* 30 0.017∓0.002 149.9740.90 variations on the lunar surface, with smaller crater [2], Klute W* 31 0.090∓0.007 216.7037.98 progressively introducing higher frequency topography. Necho* 37 0.080∓0.024 [8] 123.3 –5.3 Crater wall slopes represent most of the overall topo- Aristarchus* 40 0.175∓0.0095 312.5 23.7 graphic variation since many locations on the Moon are Jackson* 71 0.147∓0.038 [9] 196.7 22.1 craters. While impact events lead to the formation of McLaughlin 75 3.7∓0.1 [10] 267.1747.01 steep slopes [3], they are also primarily responsible for Pitiscus 80 3.8∓0.1 [10] 30.57 -50.61 landform degradation [4]. During crater formation, tar- Al-Biruni 80 3.8∓0.1 [10] 92.62 18.09 get properties and processes controlling structural sta- La Pérouse 80 3.6∓0.1 [10] -10.66 76.18 bility limit maximum slopes [4].
    [Show full text]
  • Apollo 15 Index of 70Mm Photographs
    NATIONAL AERONAUTICS AND SPACE ADMINISTRATION APOLLO 15 INDEX OF 70 mm PHOTOGRAPHS JANUARY 12, 1972 MAPPING SCIENCES BRANCH EARTH OBSERVATIONS DIVISION SCIENCE AND APPLICATIONS DIRECTORATE MANNED SPACECRAFT CENTER HOUSTON,TEXAS APOLLO 15 INDEX OF 70mm PHOTOGRAPHS January 12, 1972 Prepared for: Mapping Sciences Branch Earth Observations Division National Aeronautics and Space Administration Manned Spacecraft Center Houston, Texas Scanned and converted to PDF format by Matthew Kay [email protected] May 2002 PREFACE This report was prepared by Lockheed Electronics Company, Inc., Houston Aerospace Systems Division, under Contract NAS 9-12200, Project Work Order 63-0117-5714, and issued at the Manned Spacecraft Center, Houston, Texas. The major contributors to this document were R. G. Cook, R. A. Pinter and F. W. Solomon of the Image Analysis Section with the support of personnel of the Mapping Science Department. APOLLO 15 INDEX OF 70 MM PHOTOGRAPHS Prepared By: Lockheed Electronics Company, Inc., HASD Mapping Sciences Department For Mapping Sciences Branch of the Earth Observations Division National Aeronautics and Space Administration Manned Spacecraft Center Houston, Texas Dr. M. C. McEwen Approved By: Head, Lunar Screening & Indexing Group Mapping Sciences Branch/EOD January 12, 1972 Issue Date Apollo 15 Index of 70mm Photographs TABLE OF CONTENTS Page Introduction . 1 Sources of Information . 3 Index by NASA Photo Numbers Magazine QQ, AS15-81-10869 to 11046 . 10 Magazine SS, AS15-82-11047 to 11217 . 22 Magazine MM, AS15-84-11235 to 11352 . 34 Magazine LL, AS15-85-11353 to 11529 . 42 Magazine NN, AS15-86-11530 to 11694 . 54 Magazine KK, AS15-87-11695 to 11860 .
    [Show full text]