DOCSLIB.ORG

Bi-Gaussian Stratified Wetting Model on Rough Surfaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bi-Gaussian Stratified Wetting Model on Rough Surfaces Subscriber access provided by Imperial College London | Library New Concepts at the Interface: Novel Viewpoints and Interpretations, Theory and Computations Bi-Gaussian Stratified Wetting Model on Rough Surfaces Songtao Hu, Tom Reddyhoff, Debashis Puhan, Sorin-Cristian Vladescu, Weifeng Huang, Xi Shi, Daniele Dini, and Zhike Peng Langmuir, Just Accepted Manuscript • DOI: 10.1021/acs.langmuir.9b00107 • Publication Date (Web): 04 Apr 2019 Downloaded from http://pubs.acs.org on April 9, 2019 Just Accepted “Just Accepted” manuscripts have been peer-reviewed and accepted for publication. They are posted online prior to technical editing, formatting for publication and author proofing. The American Chemical Society provides “Just Accepted” as a service to the research community to expedite the dissemination of scientific material as soon as possible after acceptance. “Just Accepted” manuscripts appear in full in PDF format accompanied by an HTML abstract. “Just Accepted” manuscripts have been fully peer reviewed, but should not be considered the official version of record. They are citable by the Digital Object Identifier (DOI®). “Just Accepted” is an optional service offered to authors. Therefore, the “Just Accepted” Web site may not include all articles that will be published in the journal. After a manuscript is technically edited and formatted, it will be removed from the “Just Accepted” Web site and published as an ASAP article. Note that technical editing may introduce minor changes to the manuscript text and/or graphics which could affect content, and all legal disclaimers and ethical guidelines that apply to the journal pertain. ACS cannot be held responsible for errors or consequences arising from the use of information contained in these “Just Accepted” manuscripts. is published by the American Chemical Society. 1155 Sixteenth Street N.W., Washington, DC 20036 Published by American Chemical Society. Copyright © American Chemical Society. However, no copyright claim is made to original U.S. Government works, or works produced by employees of any Commonwealth realm Crown government in the course of their duties. Page 1 of 25 Langmuir 1 2 3 4 Bi-Gaussian Stratified Wetting Model on Rough Surfaces 5 6 7 Songtao Hu,† Tom Reddyhoff,‡ Debashis Puhan,‡ Sorin-Cristian Vladescu,‡ Weifeng Huang,§ Xi Shi,*,† 8 Daniele Dini,‡ Zhike Peng† 9 10 11 †State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 12 200240, China 13 ‡ 14 Department of Mechanical Engineering, Imperial College London, London SW7 2AZ, UK 15 §State Key Laboratory of Tribology, Tsinghua University, Beijing 100084, China 16 17 18 ABSTRACT: Wetting mechanisms on rough surfaces were understood from either a monolayer or a 19 multiscale perspective. However, it has recently been shown that the bi-Gaussian stratified nature of real 20 surfaces should be accounted for when modelling mechanisms of lubrication, sealing, contact, friction, 21 acoustic emission, and manufacture. In this work, a model combining Wenzel and Cassie theories was 22 23 put forward to predict the static contact angle of a droplet on a bi-Gaussian stratified surface. The model 24 was initially applied to numerically simulated surfaces, and subsequently demonstrated on hydrophilic 25 steel and hydrophobic self-assembled monolayer specimens with preset bi-Gaussian stratified 26 27 topographies. In the Wenzel state, both the upper and the lower surface components are fully wetted. In 28 the Cassie state, the upper component is still completely wetted while the lower component serves as gas 29 traps and reservoirs. By this model, wetting evolution was assessed, and the existence of different wetting 30 31 states and potential state transitions was predicted. 32 33 ■ INTRODUCTION 34 Wetting behavior occurs when a solid-gas interface transfers into a solid-liquid interface on a solid, and 35 36 it indicates the ability of the solid surface to accommodate and maintain permanent contact with the 37 liquid. Controlling the wettability of a solid is a research area of intense focus, which has resulted in a 38 significant number of applications including self-cleaning1,2, anti-icing3,4, antifogging5,6, antireflection7,8, 39 40 friction reduction9,10, etc. It is therefore of utmost importance to understand the intrinsic wetting 41 mechanism that occurs. Since Young introduced the theoretical modelling of static contact angle (CA, 42 serving as a key wetting index) on an ideal smooth surface, it has become well known that the roughness 43 44 of a surface can induce a significant effect on its wettability. Two famous hypotheses have been proposed 45 to explain the wetting mechanism of a rough surface. In the Wenzel11 case (see Figure S3a), the liquid 46 completely fills the valleys of a rough surface. The roughness extends the solid area in comparison to the 47 projected one, enhancing the intrinsic wettability of the solid (a hydrophilic surface turns into a more 48 49 hydrophilic one, while a hydrophobic surface becomes more hydrophobic). In the Cassie12 case (see 50 Figure S3b), gas is trapped into the valleys underneath the liquid, transforming the surface from a 51 continuous solid-liquid interface into a composite one consisting of solid-liquid and gas-liquid interfaces. 52 53 To date, these two theoretical models have been widely used to capture CAs on rough surfaces, however 54 these studies have been limited to scenarios of either a monolayer13−18 or a multiscale (fractal, 55 hierarchical)1925 topography. 56 57 In fact, most researchers have focused exclusively on either a Gaussian or a non-Gaussian 58 distribution of topographical heights from the view of monolayer point, overlooking the real-life case of 59 a bi-Gaussian stratified property (see Figure 1a) long-termly covered by the non-Gaussian one. As 60 ACS Paragon Plus Environment Langmuir Page 2 of 25 1 2 3 schematically illustrated in Figure 1b, a bi-Gaussian stratified surface consists of a large roughness-scale 4 5 Gaussian surface (lower component) and another Gaussian surface at a small roughness scale (upper 6 component), where the lower height is maintained on each node when combining the two components. 7 In contrast with a multiscale property emphasizing the properties (e.g., self-similarity, self-affinity) 8 exhibited by a rough surface at different scales, the bi-Gaussian one displays its two components in a 9 10 stratified (following a selective superposition rather than a direct superposition as depicted in Figure 1b) 11 formation at the same scale. 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Figure 1. Topography of a bi-Gaussian stratified surface (a) and its schematic in a profile formation (b). 33 34 The bi-Gaussian stratified property of a rough surface was initially observed on automotive cylinder 35 36 liners through a two-stage manufacturing process (plateau honing),26 and was then extended to model 37 surfaces modified by a material wear.27 Notably, the bi-Gaussian stratified property should be 38 differentiated from the mother non-Gaussian property in three ways: (1) The bi-Gaussian stratified 39 40 surface can arise from a multi-stage subtractive manufacturing process,28 indicating its widespread 41 applicability. Moreover, an active service usually induces a material wear as similar to the multi-stage 42 subtractive manufacturing process,29 thus extending the applicability. (2) The mechanism of forming the 43 44 two components is clearly associated with specific actions. Namely, the lower component is produced 45 by the early manufacturing process or is the original unused surface, while the upper component is 46 generated by the following manufacturing stage or the material wear. (3) The functional performance of 47 the two components is clearly defined in comparison to a conventional monolayer surface. For instance, 48 49 in the tribological field, the upper component plays a predominant role in load bearing and wear 50 resistance, and the lower component acts as lubricant reservoirs and debris traps. 51 By reviewing the most relevant studies in the area of surface roughness, it becomes evident that the 52 53 bi-Gaussian stratified perspective has exhibited an excellent capability in revealing the mechanisms in 54 terms of lubrication, sealing, asperity contact, friction, acoustic emission, and manufacture.28−30 However, 55 to our knowledge, it has not yet been employed to analyze the wetting mechanism of rough surfaces. In 56 57 this paper, a model combining Wenzel and Cassie theories was established to predict the static CA of a 58 droplet on a bi-Gaussian stratified surface (see section “Theoretical Model”). In particular, the model 59 contains two special cases, i.e., Wenzel and Cassie states. In section “Model Demonstration”, the model 60 ACS Paragon Plus Environment Page 3 of 25 Langmuir 1 2 3 was initially investigated on numerically simulated bi-Gaussian stratified surfaces, and subsequently 4 5 demonstrated on hydrophilic steel specimens and hydrophobic self-assembled monolayer (SAM) coated 6 specimens with prescribed bi-Gaussian stratified topographies. Furthermore, the model was used to 7 explain and predict the existence of different wetting states and potential state transitions from a bi- 8 Gaussian stratified viewpoint (see section “Discussion”). 9 10 11 ■ MODEL 12 In the Wenzel model, the CA can be described as11 13 14 15 cos * r cos , (1a) 16 17 * 18 where is the apparent CA of a droplet on a rough surface, and is the intrinsic CA on an ideal smooth 19 surface modelled by the well-known Young equation. Herein, r is the ratio of the real area to the projected 20 one, acting as the roughness factor used to assess the area extension. As the value of r is always greater 21 than 1, the intrinsic wettability of a solid will be enhanced according to the Wenzel model. When the 22 23 liquid droplet is located on a heterogeneous solid surface, the reduced Cassie model can be applied12 24 25 * cos f cos f 1 , (1b) 26 27 28 where f is the fraction of the solid-liquid interface.
Load more

Recommended publications
  • WORK PROGRAMME of General Directorate of Standardization - ALBANIA (Period 1 July to 31 December 2018)
    WORK PROGRAMME of General Directorate of Standardization - ALBANIA (Period 1 July to 31 December 2018) Technical Committee No. 1 “Quality assurance and social responsibility”, 11 standards No. Standard number English title 1. EN ISO 22300:2018 Security and resilience - Vocabulary (ISO 22300:2018) 2. CEN/TS 17159:2018 Societal and citizen security - Guidance for the security of hazardous materials (CBRNE) in healthcare facilities 3. EN ISO 9004:2018 Quality management - Quality of an organization - Guidance to achieve sustained success (ISO 9004:2018) 4. CWA 17145-2:2017 Ethics assessment for research and innovation - Part 2: Ethical impact assessment framework 5. CWA 17145-1:2017 Ethics assessment for research and innovation - Part 1: Ethics committee 6. EN ISO 41011:2018 Facility management - Vocabulary (ISO 41011:2017) 7. EN ISO 41001:2018 Facility management - Management systems - Requirements with guidance for use (ISO 41001:2018) 8. IWA 18:2016 Framework for integrated community-based life-long health and care services in aged societies 9. IWA 16:2015 International harmonized method(s) for a coherent quantification of CO2e emissions of freight transport 10. ISO/IEC Guide 17:2016 ISO/IEC Guide 17:2016Guide for writing standards taking into account the needs of micro, small and medium-sized enterprises 11. ISO 37500:2014 Guidance on outsourcing Technical Committee No. 3 “Electrical and electronical materials”, 59 standards No. Standard number English title 1. EN 50288-12-1:2017 Multi-element metallic cables used in analogue and digital communications and control - Part 12-1: Sectional specification for screened cables characterised from 1 MHz up to 2 000 MHz - 1 Horizontal and building backbone cables 2.
    [Show full text]
  • New 3D Parameters and Filtration Techniques for Surface Metrology, François Blateyron, Quality Magazine White Paper
    New 3D Parameters and Filtration Techniques for Surface Metrology François Blateyron, Director of R&D, Digital Surf, France For a long time surface metrology has been based upon contact measurement using 2D profilometers. Over the past twenty years the appearance of 3D profilometers and non-contact gauges has created a need for the standardization and formalization of the analysis of 3D surface texture. This paper presents the current status of the standardization process and includes a short description of the tools and parameters that will become available to users when work on the definition of the new standards, which is being carried out by working groups WG15 and WG16 of ISO technical committee TC213, has been completed. 1. Introduction meeting, and officially transferred to the TC213, in order to Since the first roughness meters appeared at the beginning start the standardization process. of the 1930s, the measurement of surface texture has always been based on 2D profilometry and contact gauges. 3. Towards a complete rework of all We had to wait until the beginning of the 1980s to see the surface texture standards appearance of instruments for measuring 3D surfaces, such In June 2002, the TC213 voted the creation of a new as white light interferometers and 3D profilometers working group [N499] and assigned it the task of [WHI94]. The first tools for analysing measurements developing future international standards for 3D surface generated by these instruments were developed by each texture. This group met for the first time in January 2003, in manufacturer, often extrapolating from existing tools for Cancun.
    [Show full text]
  • Roughness Control and Surface Texturing in Lubrication 8H35 9H15 Keynote Speaker D
    1 Web site www.metprops2019.org #Met&PropsLYON 2 Local Organising Committee CHAIR: Prof. Hassan Zahouani (University of Lyon, France - Halmstad University, Sweden) Prof. Cyril-Pailler Mattéi (University of Lyon, France) Prof. Haris procopiou (Université Paris I, Panthéon-Sorbonne, France) Prof Philippe Kapsa (CNRS, France) Dr. Roberto Vargiolu (Univesity of Lyon, France) Dr. Coralie Thieulin (University of Lyon, France) International Program Committee Prof. Liam Blunt (University of Huddersfield, UK) Prof. Christopher Brown (WPI Worcester Polytech Institute, USA) Prof. Thomas Kaiser (University of Hamburg, Germany) Prof. Mohamed El Mansori (Ecole Nationale Supérieure d'Arts et Métiers (ENSAM), France) Prof. Richard Leach (University of Nottingham, UK) Prof. Bengt-Göran, BG, Rosén (Halmstad University, Sweden) Dr. Ellen Schulz-Kornas, (Max Planck Weizmann Center for Integrative Archaeology and Anthropology, Germany) Prof. Tom R Thomas (Halmstad University, Sweden) Prof. Michael Wieczorowski (University of Poznan, Poland) Prof. Hassan Zahouani (University of Lyon - ENISE - Ecole Centrale de Lyon, France) International Scientific Committee A. Archenti, Royal Institute of Technology, Sweden K. Adachi, Tohoku University, Japan F. Blateyron, Digital Surf, France L. Blunt, University of Huddersfield, UK D. Butler, Nanyang Tech. Uni. NTU, Singapore C. Boulocher , Veagro-sup , France C. Brown, Worcester Polytechic Institute, USA M. El-Mansori, Ecole Nationale Superieure d'Arts et Metiers , France C. Evans, University of North Carolina - Charlotte, USA C. Giusca, National Physical Laboratory, UK S. Gröger, Chemnitz University of Technology, Germany W. Hongjun, Beijing Information Science & Technology University, China T. Kaiser University of Hamburg, Germany M. Kalin, University of Lubljana, Slovenia P. Kapsa, CNRS, France P. Krajnik, Chalmers University of Technology, Sweden R.
    [Show full text]
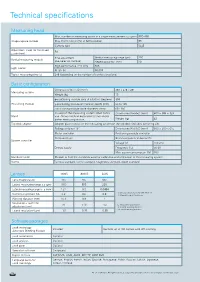
  • Technical Specifications
    Technical specifications Measuring head Max. number of measuring points in a single measurement x,y (µm2) 580x580 Image capture module Max. frame rate in (Hz) at full resolution 55 Camera type GigE Adjustment travel for motorized 50 z-axis (mm) Fine adjustment Vertical measuring range (µm) 250 Vertical measuring module (piezoelectric module) Repeat accuracy1 (nm) 10 High performance LED (nm) 505 Light source MTBF (h) 50,000 Typical measuring time (s) 2–8 (depending on the number of confocal sections) Basic configuration Dimensions W×H×D (mm3) 281 x 678 x 281 Measuring system Weight (kg) 15 φ-positioning module (axis of rotation) (degrees) 355 Positioning module y-positioning module (immersion depth) (mm) up to 165 z-positioning module (bore diameter) (mm) 68 - 150 To support the measuring system when not in Dimensions W×H×D (mm3) 600 × 384 × 324 Stand use. Allows modular expansion to liner and/or piston measuring station. Weight (kg) 62 Top deck adapter Adapter plate to position the measuring system on the top deck (includes centering aid) Rolling container 19“ Dimensions W×H×D (mm3) 600 × 600 × 615 Motor controller Positioning module controller Computer type Brand computer / industrial PC System controller Voltage (V) 100-240 Energy supply Frequency (Hz) 50-60 Max. power consumption (W) 700 Standard holder Module to hold the standards used for calibration and verification of the measuring system. Norms Flatness standard, lateral standard, roughness standard, depth standard Lenses 1600S 800XS 320S Lens magnification 10× 20× 50× Lateral measuring range x,y (µm) 110 0 550 220 Lateral measuring range x ∙ y (mm2) 1.21 0.3 0.0484 1) Measurement noise to VDI 2655-1.2 Numerical aperture NA 0.3 0.6 0.8 2) Measuring point distance Working distance (mm) 10.1 0.9 1 Resolution z1 with fine 20 <10 <2 L: long working distance adjustment (nm) S: normal working distance Lateral resolution2 (µm) 1.
    [Show full text]
  • NIST SURFACE ROUGHNESS and STEP HEIGHT CALIBRATIONS, Measurement Conditions and Sources of Uncertainty T.V
    NIST SURFACE ROUGHNESS AND STEP HEIGHT CALIBRATIONS, Measurement Conditions and Sources of Uncertainty T.V. Vorburger, T. Brian Renegar, A.X. Zheng, J-F. Song, J.A. Soons, and R.M. Silver Parameters of surface roughness and step height are currently measured at the National Institute of Standards and Technology (NIST) by means of a computerized/stylus instrument. For roughness height parameters, we use a calibration ball as a master to calibrate the instrument to be employed during a measurement. Profiles of the calibrating master and the roughness sample under test are stored in a computer. For roughness spacing parameters, we use an interferometrically calibrated Standard Reference Material (SRM) to check the calibration of the drive-axis encoder of the stylus instrument. In measurement of roughness, surface profiles are taken with a lateral sampling interval of 0.125 m, typically over an evaluation length of 4 mm. Three parameters of the instrumentation are important in the specification of roughness measurements. These are the roughness filter long wavelength cutoff (λc), the roughness filter short wavelength cutoff (λs), and the stylus radius. The nominal filter cutoff λc is 0.8 mm, and the nominal filter cutoff λs is 2.5 m. These filter transmission characteristics are in accordance with the phase-correct Gaussian filter described in ASME B46.1-2009.[1] The stylus has a radius of 1.52 µm ± 0.15 µm (with a coverage factor k = 2), calibrated by measuring a standard wire with a calibrated radius and by the razor blade trace method[1-6]. An iterative computer algorithm[5,6] is used to calculate the effective radius from the razor blade trace method.
    [Show full text]
  • Optical 3D Microscopy EN See More
    Optical 3D Microscopy EN see more Optical 3D surface metrology for industry and research Research & Process Production Development control control The μsurf platform – one technology, many benefits Maximum performance Combination of high measurement point density and measurements within seconds High precision with 16Bit HDR-technology Modern imaging sensors, high-performance optics and linear encoders for standard-compliant measurements Real 3D measurement data Physical data aquisition with patented confocal multi-pinhole technology Intuitive operation Well-thought out operating concept and ergonomic workplace solutions Easy automation User-independent serial measurements compliant with industry requirements Robust construction High level of repeatability due to practically conceived industrial design High level of flexibility Modular hardware component design, powerful software solutions and standardized interfaces 2 3 Quality and standard compliance f The innovative μsurf technology delivers high resolution 3D mea- surements of surfaces. It thus enables new insights into surface structures and treatment processes. f The confocal principle used in the surface measurement allows the data to be presented as true height coordinates (x, y, z). A precise evaluation is only possible with this quantitative information. f Numerous ISO-compliant profile and surface parameters ensure the comparability and usability of the results, both in R&D and in production. f NanoFocus always implements the latest standards in measuring systems and software. Hardness indentation SEC Speed and flexibility f The fast image acquisition of μsurf systems delivers high resolution 3D data sets in only a few seconds. f Additionally, the sample preparation required by other technologies can be dispensed with (e.g. anti-reflective coatings or sputtering).
    [Show full text]
  • Authentieke Versie
    Nr. 65440 16 november STAATSCOURANT 2017 Officiële uitgave van het Koninkrijk der Nederlanden sinds 1814. Nieuwe normen NEN Overzicht van nieuwe publicaties van het Nederlands Normalisatie-Instituut, inclusief de Europese normen, in de periode van 5 oktober 2017 tot en met 9 november 2017. De normbladen kunnen worden besteld bij NEN-Klantenservice, tel. 015-2690391, waar men ook met vragen terecht kan. Tevens kunnen de genoemde normen via internet besteld worden (www.nen.nl). Correspondentieadres: Postbus 5059, 2600 GB Delft. Document number Title AgroFood & Consument NEN-EN 1176-1:2017 en Speeltoestellen en bodemoppervlak van speelplaatsen – Deel 1: Algemene veiligheidseisen en beproevingsmethoden NEN-EN 1176-2:2017 en Speeltoestellen en bodemoppervlakken van speelplaatsen – Deel 2: Aanvul- lende bijzondere veiligheidseisen en beproevingsmethoden voor schommels NEN-EN 1176-3:2017 en Speeltoestellen en bodemoppervlakken van speelplaatsen – Deel 3: Aanvul- lende bijzondere veiligheidseisen en beproevingsmethoden voor glijbanen NEN-EN 1176-4:2017 en Speeltoestellen en bodemoppervlakken van speeltoestellen – Deel 4: Aanvul- lende bijzondere veiligheidseisen en beproevingsmethoden voor kabelbanen NEN-EN 1176-6:2017 en Speeltoestellen en bodemoppervlakken van speelplaatsen – Deel 6: Aanvul- lende bijzondere veiligheidseisen en beproevingsmethoden voor wiptoestellen NEN-EN 12944-3:2017 Ontw. en Meststoffen en kalkmeststoffen – Woordenlijst – Deel 3: Termen gerelateerd aan kalkmeststoffen Commentaar voor: 2017-12-04 NEN-EN 13329:2016+A1:2017 en Laminaatvloerbedekkingen – Elementen met een oppervlaktelaag gebaseerd op aminoplastische thermohardende harsen – Specificaties, eisen en beproevings- methoden NEN-EN 14069:2017 en Kalkmeststoffen – Aanduiding, specificaties en labelling NEN-EN 14215:2017 Ontw. en Tapijten – Classificatie van machinaal vervaardigde pooltapijten en lopers Commentaar voor: 2017-12-04 NEN-EN 15194:2017 en Fietsen – Elektrisch ondersteunde fietsen – EPAC Fietsen NEN-EN 16711-3:2017 Ontw.
    [Show full text]
  • Material Interactions in Laser Polishing Powder Bed Additive Manufactured Ti6al4v Components
    Heriot-Watt University Research Gateway Material interactions in laser polishing powder bed additive manufactured Ti6Al4V components Citation for published version: Tian, Y, Góra, WS, Pan Cabo, A, Parimi, LL, Hand, DP, Tammas-Williams, S & Prangnell, PB 2018, 'Material interactions in laser polishing powder bed additive manufactured Ti6Al4V components', Additive Manufacturing, vol. 20, pp. 11-22. https://doi.org/10.1016/j.addma.2017.12.010 Digital Object Identifier (DOI): 10.1016/j.addma.2017.12.010 Link: Link to publication record in Heriot-Watt Research Portal Document Version: Peer reviewed version Published In: Additive Manufacturing General rights Copyright for the publications made accessible via Heriot-Watt Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy Heriot-Watt University has made every reasonable effort to ensure that the content in Heriot-Watt Research Portal complies with UK legislation. If you believe that the public display of this file breaches copyright please contact [email protected] providing details, and we will remove access to the work immediately and investigate your claim. Download date: 29. Sep. 2021 Material Interactions in Laser Polishing Powder Bed Additive Manufactured Ti6Al4V Components Yingtao Tian1, Wojciech S. Gora2, Aldara Pan Cabo2, Lakshmi L. Parimi3, Duncan P. Hand2, Samuel Tammas-Williams1, Philip B. Prangnell1 1 School of Materials, University of Manchester, Manchester, M13 9PL, UK 2 School of Engineering & Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK 3 GKN Aerospace, Filton, Bristol, BS34 9AU, UK Abstract Laser polishing (LP) is an emerging technique with the potential to be used for post-build, or in-situ, precision smoothing of rough fatigue-initiation prone surfaces of additive manufactured (AM) components.
    [Show full text]
  • Isoupdate April 2019
    ISO Update Supplement to ISOfocus April 2019 International Standards in process ISO/CD 6647-2 Rice — Amylose content — Part 2: Determina- tion of absolute amylose An International Standard is the result of an agreement between ISO/CD 23942 Determination of hydroxytyrosol and tyro- the member bodies of ISO. A first important step towards an Interna- sol content in extra virgin olive oils — HPLC tional Standard takes the form of a committee draft (CD) - this is cir- method culated for study within an ISO technical committee. When consensus ISO/CD 20784 Guidance on substantiation for sensory and has been reached within the technical committee, the document is consumer claims sent to the Central Secretariat for processing as a draft International Standard (DIS). The DIS requires approval by at least 75 % of the TC 35 Paints and varnishes member bodies casting a vote. A confirmation vote is subsequently ISO/CD Preparation of steel substrates before applica- carried out on a final draft International Standard (FDIS), the approval 11127-1 tion of paints and related products — Test criteria remaining the same. methods for non-metallic blast-cleaning abra- sives — Part 1: Sampling ISO/CD Preparation of steel substrates before applica- 11127-2 tion of paints and related products — Test methods for non-metallic blast-cleaning abra- sives — Part 2: Determination of particle size distribution ISO/CD Preparation of steel substrates before applica- 11127-3 tion of paints and related products — Test CD registered methods for non-metallic blast-cleaning abrasives — Part 3: Determination of apparent density Period from 01 March to 31 March 2019 ISO/CD Preparation of steel substrates before applica- These documents are currently under consideration in the technical 11127-4 tion of paints and related products — Test committee.
    [Show full text]
  • Web-Based Reference Software for Characterisation of Surface Roughness
    Web-Based Reference Software For Characterisation Of Surface Roughness Dem Fachbereich Maschinenbau und Verfahrenstechnik der technischen Universität Kaiserslautern zur Erlangung des akademischen Grades Doktor-Ingenieur (Dr.-Ing.) vorgelegte Dissertation von Frau M.Sc. Bini Alapurath George aus Bangalore Datum der wissenschaftlichen Aussprache: 28.09.2017 Betreuer der Dissertation: Prof. Dr.-Ing. Jörg Seewig D 386 II Acknowledgment Firstly, I would like to express my gratitude and sincere thanks to my doctoral advisor Prof. Dr.-Ing. Jörg Seewig for his advice and guidance during my research and for giving me the opportunity to pursue my PhD. I would like to thank my colleagues from the Institute of Measurement and Sensor Technology for the support and discussions during my research. I wish to extend my thanks to Mr. Timo Wiegel for supporting me with my research, as part of his internship program in the Institute of Measurement and Sensor Tech- nology, T.U. Kaiserslautern during summer 2012. I am thankful to my husband, Dr. Mahesh Poolakkaparambil for his support and encouragement. A special thanks to my mother, Valsala George for her love and prayers. I am indebted to them for their help and support. I take this opportunity to thank all my friends for the memorable time during my stay in Kaiserslautern. Finally, I would like to assert that all the contents and pictures in this thesis are from the knowledge of literatures, publications and paper, which are mentioned in the references and naturally my knowledge from the study and research in this work. Kaiserslautern, __________________ Signature: ______________________ III Abstract This research explores the development of web based reference software for char- acterisation of surface roughness for two-dimensional surface data.
    [Show full text]
  • Statistical Processing and Analysis of Surface Topography Data for a Machine-Based Evaluation of the Measurement Uncertainty”
    Politecnico di Torino Corso di Laurea Magistrale in Ingegneria Meccanica Tesi di Laurea Magistrale “Statistical processing and analysis of surface topography data for a machine-based evaluation of the measurement uncertainty” Relatore Candidato prof. Gianfranco Genta Matteo Gilardi Corelatore prof. Danilo Quagliotti Anno Accademico 2019/2020 Matteo Gilardi - s254951 Matteo Gilardi - s254951 ABSTRACT Surface measurements in industrial activities are required principally to check tolerances or to characterise the surface functionality of components. There are many engineering application in which surface metrology carry out an important role (e.g. electronics, information technology, energy, optics, tribology, biology, biomimetics, etc.), but focusing only on autonomous manufacturing processes, in a perspective of what is called Industry 4.0, the areas of interest are the in-line quality check and the analysis of additive manufacturing processes with the aim of understanding and governing them. To achieve these, it is required that the measurement is acquired and processed quickly, hence, recently the optical instruments have been adopted more and more. Measurement to be reliable has to be coupled with its uncertainty; however rarely areal surface measurements presents this value. Indeed, a standard infrastructure for the traceability of areal surface measurement is still missing. This is probably due to both the complexity of the measurand and the optical instruments, whose interaction with the component is still not completely known. Hence, this project aims to cope with the complexity of such measurands by exploring applicability and limitations of methods for an autonomous, machine-based, statistical evaluation of the measurement uncertainty. First of all, the surfaces are processed in order to remove the form and manage possible non-measured points and/or spikes.
    [Show full text]
  • Procedure for Calibrating the Z-Axis of a Confocal Microscope: Application for the Evaluation of Structured Surfaces
    sensors Article Procedure for Calibrating the Z-axis of a Confocal Microscope: Application for the Evaluation of Structured Surfaces Chen Wang, Jesús Caja , Emilio Gómez and Piera Maresca * Escuela Técnica Superior de Ingeniería y Diseño Industrial, Universidad Politécnica de Madrid, Ronda de Valencia 3, 28012 Madrid, Spain; [email protected] (C.W.); [email protected] (J.C.); [email protected] (E.G.) * Correspondence: [email protected]; Tel.: +34-910-677-688 Received: 19 December 2018; Accepted: 24 January 2019; Published: 27 January 2019 Abstract: This work describes a method for the metrological characterization of structured surfaces using a confocal microscope. The proposed method is based on the calculation of texture parameters established in ISO 25178-2:2012. To ensure the traceability of these parameters, a procedure for the calibration of the Z-axis of the confocal microscope is proposed. The calculation of uncertainty associated with each parameter employs the Monte Carlo method, as well as the concept of a virtual instrument. The validity of the algorithms has been verified through the use of synthetic data provided by the National Institute of Standards and Technology (NIST) and physical standards, with minimum differences being obtained between the certified values and calculated or measured values. Finally, using the proposed method, the topography of a structured surface manufactured by laser machining is evaluated, obtaining the most used roughness parameters, as well as their measurement uncertainties and possible correlations. In general, it can be affirmed that it is possible to obtain metrologically reliable results with the proposed method. Keywords: areal surface texture; confocal microscopy; uncertainty evaluation; structured surface 1.
    [Show full text]