Lecture 26. Bose-Einstein Condensation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Competition Between Paramagnetism and Diamagnetism in Charged
Competition between paramagnetism and diamagnetism in charged Fermi gases Xiaoling Jian, Jihong Qin, and Qiang Gu∗ Department of Physics, University of Science and Technology Beijing, Beijing 100083, China (Dated: November 10, 2018) The charged Fermi gas with a small Lande-factor g is expected to be diamagnetic, while that with a larger g could be paramagnetic. We calculate the critical value of the g-factor which separates the dia- and para-magnetic regions. In the weak-field limit, gc has the same value both at high and low temperatures, gc = 1/√12. Nevertheless, gc increases with the temperature reducing in finite magnetic fields. We also compare the gc value of Fermi gases with those of Boltzmann and Bose gases, supposing the particle has three Zeeman levels σ = 1, 0, and find that gc of Bose and Fermi gases is larger and smaller than that of Boltzmann gases,± respectively. PACS numbers: 05.30.Fk, 51.60.+a, 75.10.Lp, 75.20.-g I. INTRODUCTION mK and 10 µK, respectively. The ions can be regarded as charged Bose or Fermi gases. Once the quantum gas Magnetism of electron gases has been considerably has both the spin and charge degrees of freedom, there studied in condensed matter physics. In magnetic field, arises the competition between paramagnetism and dia- the magnetization of a free electron gas consists of two magnetism, as in electrons. Different from electrons, the independent parts. The spin magnetic moment of elec- g-factor for different magnetic ions is diverse, ranging trons results in the paramagnetic part (the Pauli para- from 0 to 2. -

Solid State Physics 2 Lecture 5: Electron Liquid
Physics 7450: Solid State Physics 2 Lecture 5: Electron liquid Leo Radzihovsky (Dated: 10 March, 2015) Abstract In these lectures, we will study itinerate electron liquid, namely metals. We will begin by re- viewing properties of noninteracting electron gas, developing its Greens functions, analyzing its thermodynamics, Pauli paramagnetism and Landau diamagnetism. We will recall how its thermo- dynamics is qualitatively distinct from that of a Boltzmann and Bose gases. As emphasized by Sommerfeld (1928), these qualitative di↵erence are due to the Pauli principle of electons’ fermionic statistics. We will then include e↵ects of Coulomb interaction, treating it in Hartree and Hartree- Fock approximation, computing the ground state energy and screening. We will then study itinerate Stoner ferromagnetism as well as various response functions, such as compressibility and conduc- tivity, and screening (Thomas-Fermi, Debye). We will then discuss Landau Fermi-liquid theory, which will allow us understand why despite strong electron-electron interactions, nevertheless much of the phenomenology of a Fermi gas extends to a Fermi liquid. We will conclude with discussion of electrons on the lattice, treated within the Hubbard and t-J models and will study transition to a Mott insulator and magnetism 1 I. INTRODUCTION A. Outline electron gas ground state and excitations • thermodynamics • Pauli paramagnetism • Landau diamagnetism • Hartree-Fock theory of interactions: ground state energy • Stoner ferromagnetic instability • response functions • Landau Fermi-liquid theory • electrons on the lattice: Hubbard and t-J models • Mott insulators and magnetism • B. Background In these lectures, we will study itinerate electron liquid, namely metals. In principle a fully quantum mechanical, strongly Coulomb-interacting description is required. -

Chapter 3 Bose-Einstein Condensation of an Ideal
Chapter 3 Bose-Einstein Condensation of An Ideal Gas An ideal gas consisting of non-interacting Bose particles is a ¯ctitious system since every realistic Bose gas shows some level of particle-particle interaction. Nevertheless, such a mathematical model provides the simplest example for the realization of Bose-Einstein condensation. This simple model, ¯rst studied by A. Einstein [1], correctly describes important basic properties of actual non-ideal (interacting) Bose gas. In particular, such basic concepts as BEC critical temperature Tc (or critical particle density nc), condensate fraction N0=N and the dimensionality issue will be obtained. 3.1 The ideal Bose gas in the canonical and grand canonical ensemble Suppose an ideal gas of non-interacting particles with ¯xed particle number N is trapped in a box with a volume V and at equilibrium temperature T . We assume a particle system somehow establishes an equilibrium temperature in spite of the absence of interaction. Such a system can be characterized by the thermodynamic partition function of canonical ensemble X Z = e¡¯ER ; (3.1) R where R stands for a macroscopic state of the gas and is uniquely speci¯ed by the occupa- tion number ni of each single particle state i: fn0; n1; ¢ ¢ ¢ ¢ ¢ ¢g. ¯ = 1=kBT is a temperature parameter. Then, the total energy of a macroscopic state R is given by only the kinetic energy: X ER = "ini; (3.2) i where "i is the eigen-energy of the single particle state i and the occupation number ni satis¯es the normalization condition X N = ni: (3.3) i 1 The probability -
![Arxiv:2102.13616V2 [Cond-Mat.Quant-Gas] 30 Jul 2021 That Preserve Stability of the Underlying Problem1](https://docslib.b-cdn.net/cover/6442/arxiv-2102-13616v2-cond-mat-quant-gas-30-jul-2021-that-preserve-stability-of-the-underlying-problem1-456442.webp)
Arxiv:2102.13616V2 [Cond-Mat.Quant-Gas] 30 Jul 2021 That Preserve Stability of the Underlying Problem1
Self-stabilized Bose polarons Richard Schmidt1, 2 and Tilman Enss3 1Max-Planck-Institute of Quantum Optics, Hans-Kopfermann-Straße 1, 85748 Garching, Germany 2Munich Center for Quantum Science and Technology, Schellingstraße 4, 80799 Munich, Germany 3Institut f¨urTheoretische Physik, Universit¨atHeidelberg, 69120 Heidelberg, Germany (Dated: August 2, 2021) The mobile impurity in a Bose-Einstein condensate (BEC) is a paradigmatic many-body problem. For weak interaction between the impurity and the BEC, the impurity deforms the BEC only slightly and it is well described within the Fr¨ohlich model and the Bogoliubov approximation. For strong local attraction this standard approach, however, fails to balance the local attraction with the weak repulsion between the BEC particles and predicts an instability where an infinite number of bosons is attracted toward the impurity. Here we present a solution of the Bose polaron problem beyond the Bogoliubov approximation which includes the local repulsion between bosons and thereby stabilizes the Bose polaron even near and beyond the scattering resonance. We show that the Bose polaron energy remains bounded from below across the resonance and the size of the polaron dressing cloud stays finite. Our results demonstrate how the dressing cloud replaces the attractive impurity potential with an effective many-body potential that excludes binding. We find that at resonance, including the effects of boson repulsion, the polaron energy depends universally on the effective range. Moreover, while the impurity contact is strongly peaked at positive scattering length, it remains always finite. Our solution highlights how Bose polarons are self-stabilized by repulsion, providing a mechanism to understand quench dynamics and nonequilibrium time evolution at strong coupling. -

Scientific and Related Works of Chen Ning Yang
Scientific and Related Works of Chen Ning Yang [42a] C. N. Yang. Group Theory and the Vibration of Polyatomic Molecules. B.Sc. thesis, National Southwest Associated University (1942). [44a] C. N. Yang. On the Uniqueness of Young's Differentials. Bull. Amer. Math. Soc. 50, 373 (1944). [44b] C. N. Yang. Variation of Interaction Energy with Change of Lattice Constants and Change of Degree of Order. Chinese J. of Phys. 5, 138 (1944). [44c] C. N. Yang. Investigations in the Statistical Theory of Superlattices. M.Sc. thesis, National Tsing Hua University (1944). [45a] C. N. Yang. A Generalization of the Quasi-Chemical Method in the Statistical Theory of Superlattices. J. Chem. Phys. 13, 66 (1945). [45b] C. N. Yang. The Critical Temperature and Discontinuity of Specific Heat of a Superlattice. Chinese J. Phys. 6, 59 (1945). [46a] James Alexander, Geoffrey Chew, Walter Salove, Chen Yang. Translation of the 1933 Pauli article in Handbuch der Physik, volume 14, Part II; Chapter 2, Section B. [47a] C. N. Yang. On Quantized Space-Time. Phys. Rev. 72, 874 (1947). [47b] C. N. Yang and Y. Y. Li. General Theory of the Quasi-Chemical Method in the Statistical Theory of Superlattices. Chinese J. Phys. 7, 59 (1947). [48a] C. N. Yang. On the Angular Distribution in Nuclear Reactions and Coincidence Measurements. Phys. Rev. 74, 764 (1948). 2 [48b] S. K. Allison, H. V. Argo, W. R. Arnold, L. del Rosario, H. A. Wilcox and C. N. Yang. Measurement of Short Range Nuclear Recoils from Disintegrations of the Light Elements. Phys. Rev. 74, 1233 (1948). [48c] C. -

The Two-Dimensional Bose Gas in Box Potentials Laura Corman
The two-dimensional Bose Gas in box potentials Laura Corman To cite this version: Laura Corman. The two-dimensional Bose Gas in box potentials. Physics [physics]. Université Paris sciences et lettres, 2016. English. NNT : 2016PSLEE014. tel-01449982 HAL Id: tel-01449982 https://tel.archives-ouvertes.fr/tel-01449982 Submitted on 30 Jan 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THÈSE DE DOCTORAT de l’Université de recherche Paris Sciences Lettres – PSL Research University préparée à l’École normale supérieure The Two-Dimensional Bose École doctorale n°564 Gas in Box Potentials Spécialité: Physique Soutenue le 02.06.2016 Composition du Jury : par Laura Corman M Tilman Esslinger ETH Zürich Rapporteur Mme Hélène Perrin Université Paris XIII Rapporteur M Zoran Hadzibabic Cambridge University Membre du Jury M Gilles Montambaux Université Paris XI Membre du Jury M Jean Dalibard Collège de France Directeur de thèse M Jérôme Beugnon Université Paris VI Membre invité ABSTRACT Degenerate atomic gases are a versatile tool to study many-body physics. They offer the possibility to explore low-dimension physics, which strongly differs from the three dimensional (3D) case due to the enhanced role of fluctuations. -
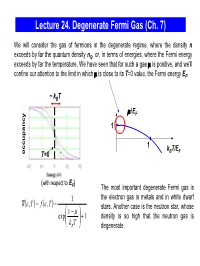
Lecture 24. Degenerate Fermi Gas (Ch
Lecture 24. Degenerate Fermi Gas (Ch. 7) We will consider the gas of fermions in the degenerate regime, where the density n exceeds by far the quantum density nQ, or, in terms of energies, where the Fermi energy exceeds by far the temperature. We have seen that for such a gas μ is positive, and we’ll confine our attention to the limit in which μ is close to its T=0 value, the Fermi energy EF. ~ kBT μ/EF 1 1 kBT/EF occupancy T=0 (with respect to E ) F The most important degenerate Fermi gas is 1 the electron gas in metals and in white dwarf nε()(),, T= f ε T = stars. Another case is the neutron star, whose ε⎛ − μ⎞ exp⎜ ⎟ +1 density is so high that the neutron gas is ⎝kB T⎠ degenerate. Degenerate Fermi Gas in Metals empty states ε We consider the mobile electrons in the conduction EF conduction band which can participate in the charge transport. The band energy is measured from the bottom of the conduction 0 band. When the metal atoms are brought together, valence their outer electrons break away and can move freely band through the solid. In good metals with the concentration ~ 1 electron/ion, the density of electrons in the electron states electron states conduction band n ~ 1 electron per (0.2 nm)3 ~ 1029 in an isolated in metal electrons/m3 . atom The electrons are prevented from escaping from the metal by the net Coulomb attraction to the positive ions; the energy required for an electron to escape (the work function) is typically a few eV. -

Chapter 13 Ideal Fermi
Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k T µ,βµ 1, B � � which defines the degenerate Fermi gas. In this limit, the quantum mechanical nature of the system becomes especially important, and the system has little to do with the classical ideal gas. Since this chapter is devoted to fermions, we shall omit in the following the subscript ( ) that we used for the fermionic statistical quantities in the previous chapter. − 13.1 Equation of state Consider a gas ofN non-interacting fermions, e.g., electrons, whose one-particle wave- functionsϕ r(�r) are plane-waves. In this case, a complete set of quantum numbersr is given, for instance, by the three cartesian components of the wave vector �k and thez spin projectionm s of an electron: r (k , k , k , m ). ≡ x y z s Spin-independent Hamiltonians. We will consider only spin independent Hamiltonian operator of the type ˆ 3 H= �k ck† ck + d r V(r)c r†cr , �k � where thefirst and the second terms are respectively the kinetic and th potential energy. The summation over the statesr (whenever it has to be performed) can then be reduced to the summation over states with different wavevectork(p=¯hk): ... (2s + 1) ..., ⇒ r � �k where the summation over the spin quantum numberm s = s, s+1, . , s has been taken into account by the prefactor (2s + 1). − − 159 160 CHAPTER 13. IDEAL FERMI GAS Wavefunctions in a box. We as- sume that the electrons are in a vol- ume defined by a cube with sidesL x, Ly,L z and volumeV=L xLyLz. -

Bose Polarons at Finite Temperature and Strong Coupling
Bose polarons at finite temperature and strong coupling Pietro Massignan Outline ✦ Quantum mixtures ✦ Impurities in an ideal Fermi sea (“Fermi polarons”) ✦ Impurities in a weakly-interacting Bose gas (“Bose polarons”) ✦ Zero-temperature physics ✦ New features appearing at non-zero temperature Collaborators Nils Guenther Maciej Lewenstein Georg M. Bruun Quantum Mixtures in CondMat 3He-4He ultracold gaseous mixtures: FF (BEC-BCS crossover) [Zwerger, Lecture Notes in Phys.] B+FF superfluids (coherent/damped dynamics) ENS-Paris BB mixtures (ultradilute quantum liquid droplets) Stuttgart, Innsbruck, Barcelona spinor gases, SU(N) invariant systems Kyoto, Florence, Munich, … quantum magnets, quantum Hall systems, spin-liquids quark-gluon plasma neutron stars Very different microscopically, but ∃ common emergent and universal many-body descriptions. 4 Universality in Quantum Mixtures 20 orders of magnitude difference in temperature Coulomb plasma but similar transport properties! e.g., shear viscosity/entropy density: [Adams et al., NJP 2012] 5 Many-body systems (from Richard Mattuck’s book) 6 Quasi-Particles No chance of studying real particles Landau: of importance are the collective excitations, which generally behave as quasi-particles! a QP is a “free” particle with: @ q. numbers (charge, spin, ...) @ renormalized mass @ chemical potential @ shielded interactions @ lifetime 7 Ultracold atoms chemical composition interaction strength temperature periodic potentials physical dimension atom-light coupling exotic interactions (x-wave, spin-orbit) dynamics disorder periodic driving (shaken optical lattices) 8 Imbalanced Fermi gases Two-component Fermi gas with N↑≫N↓: a strongly-interacting system, or an ensemble of weakly-interacting quasi-particles (a Fermi liquid) 3 m N 5/3 E = ✏F N 1+ # + N Ep + ..., 5 " m⇤ N # " ✓ " ◆ # kinetic energy chemical potential (energy) kinetic energy of one polaron of the Fermi sea of the polarons (m* is their effective mass) 9 Spectrum of Fermi polarons low power RF: high power RF: repulsive pol. -

Electron-Electron Interactions(Pdf)
Contents 2 Electron-electron interactions 1 2.1 Mean field theory (Hartree-Fock) ................ 3 2.1.1 Validity of Hartree-Fock theory .................. 6 2.1.2 Problem with Hartree-Fock theory ................ 9 2.2 Screening ..................................... 10 2.2.1 Elementary treatment ......................... 10 2.2.2 Kubo formula ............................... 15 2.2.3 Correlation functions .......................... 18 2.2.4 Dielectric constant ............................ 19 2.2.5 Lindhard function ............................ 21 2.2.6 Thomas-Fermi theory ......................... 24 2.2.7 Friedel oscillations ............................ 25 2.2.8 Plasmons ................................... 27 2.3 Fermi liquid theory ............................ 30 2.3.1 Particles and holes ............................ 31 2.3.2 Energy of quasiparticles. ....................... 36 2.3.3 Residual quasiparticle interactions ................ 38 2.3.4 Local energy of a quasiparticle ................... 42 2.3.5 Thermodynamic properties ..................... 44 2.3.6 Quasiparticle relaxation time and transport properties. 46 2.3.7 Effective mass m∗ of quasiparticles ................ 50 0 Reading: 1. Ch. 17, Ashcroft & Mermin 2. Chs. 5& 6, Kittel 3. For a more detailed discussion of Fermi liquid theory, see G. Baym and C. Pethick, Landau Fermi-Liquid Theory : Concepts and Ap- plications, Wiley 1991 2 Electron-electron interactions The electronic structure theory of metals, developed in the 1930’s by Bloch, Bethe, Wilson and others, assumes that electron-electron interac- tions can be neglected, and that solid-state physics consists of computing and filling the electronic bands based on knowldege of crystal symmetry and atomic valence. To a remarkably large extent, this works. In simple compounds, whether a system is an insulator or a metal can be deter- mined reliably by determining the band filling in a noninteracting cal- culation. -

Dynamic Correlations in a Charged Bose Gas
XA9745097 IC/97/95 INTERNATIONAL CENTRE FOR THEORETICAL PHYSICS DYNAMIC CORRELATIONS IN A CHARGED BOSE GAS K. Tankeshwar B. Tanatar and M.P. Tosi MIRAMARE-TRIESTE IC/97/95 United Nations Educational Scientific and Cultural Organization and International Atomic Energy Agency INTERNATIONAL CENTRE FOR THEORETICAL PHYSICS DYNAMIC CORRELATIONS IN A CHARGED BOSE GAS K. Tankeshwar Center for Advanced Study in Physics, Department of Physics, Panjab University, 160 014 Chandigarh, India and International Centre for Theoretical Physics, Trieste, Italy, B. Tanatar1 Department of Physics, Bilkent University, Bilkent, 06533 Ankara, Turkey and International Centre for Theoretical Physics, Trieste, Italy and M.P. Tosi2 Scuola Normale Superiore, 1-56126 Pisa, Italy and International Centre for Theoretical Physics, Trieste, Italy. MIRAMARE - TRIESTE August 1997 1 Regular Associate of the ICTP. 2 On leave of absence. ABSTRACT We evaluate the ground state properties of a charged Bose gas at T = 0 within the quan tum version of the self-consistent field approximation of Singwi, Tosi, Land and Sjolander (STLS). The dynamical nature of the local field correction is retained to include dynamic correlation effects. The resulting static structure factor S(q) and the local field factor Ci(q) exhibit properties not described by other mean-field theories. 1 I. INTRODUCTION The homogeneous gas of electrons interacting via the Coulomb potential is a useful model1 to understand a vast range of physical phenomena. The continuing interest in this model stems partly from the realization of physical systems in the laboratory which lend themselves to such a description, and partly from theoretical reasons to understand the basic properties of a many body system. -

The Non-Interacting Bose Gas
Chapter 1 The non-interacting Bose gas Learning goals What is a Bose-Einstein condensate and why does it form? • What determines the critical temperature and the condensate fraction? • What changes for trapped systems? • The ideal, i.e. non-interacting Bose gas is the starting point for our discussions. Its properties are determined by the quantum statistics of the particles. In the grand canonical ensemble, we can write down the Bose distribution function, which leads to a criterion for Bose-Einstein con- densation. We define the critical temperature and the condensate fraction for the homogeneous gas before we turn to the experimentally relevant case of a gas trapped in a harmonic potential. 1.1 Introduction 1.1.1 Quantum statistics Quantum statistics tells us how to distribute particles on possible quantum states. It is essen- tially determined by the symmetry of the wave function upon a permutation of the particles. As the most simple example, we consider two particles which can be distributed in two boxes (quan- tum states), see Fig. 1.1. If the particles are distinguishable, in total four di↵erent possibilities exist. The probability to find two particles in the same state is then 1/2. This changes if we consider two indistinguishable bosons. Now, only three di↵erent combinations are possible, and the situation that two bosons occupy the same quantum state is enhanced to 2/3 - bosons tend to stick together! This is in contrast to fermions, where the Pauli exclusion principle prohibits the possibility of two particles being in the same state and only one possibility to arrange the particles exists.