DOCSLIB.ORG

Competition Between Paramagnetism and Diamagnetism in Charged

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Competition Between Paramagnetism and Diamagnetism in Charged Competition between paramagnetism and diamagnetism in charged Fermi gases Xiaoling Jian, Jihong Qin, and Qiang Gu∗ Department of Physics, University of Science and Technology Beijing, Beijing 100083, China (Dated: November 10, 2018) The charged Fermi gas with a small Lande-factor g is expected to be diamagnetic, while that with a larger g could be paramagnetic. We calculate the critical value of the g-factor which separates the dia- and para-magnetic regions. In the weak-field limit, gc has the same value both at high and low temperatures, gc = 1/√12. Nevertheless, gc increases with the temperature reducing in finite magnetic fields. We also compare the gc value of Fermi gases with those of Boltzmann and Bose gases, supposing the particle has three Zeeman levels σ = 1, 0, and find that gc of Bose and Fermi gases is larger and smaller than that of Boltzmann gases,± respectively. PACS numbers: 05.30.Fk, 51.60.+a, 75.10.Lp, 75.20.-g I. INTRODUCTION mK and 10 µK, respectively. The ions can be regarded as charged Bose or Fermi gases. Once the quantum gas Magnetism of electron gases has been considerably has both the spin and charge degrees of freedom, there studied in condensed matter physics. In magnetic field, arises the competition between paramagnetism and dia- the magnetization of a free electron gas consists of two magnetism, as in electrons. Different from electrons, the independent parts. The spin magnetic moment of elec- g-factor for different magnetic ions is diverse, ranging trons results in the paramagnetic part (the Pauli para- from 0 to 2. magnetism), while the orbital motion due to charge de- The g-factor is a characteristic parameter to measure gree of freedom in magnetic field induces the diamagnetic the intensity of paramagnetic effect. It is expected that part (the Landau diamagnetism)[1]. The Pauli paramag- the quantum gas displays diamagnetism in small g region, netism and the Landau diamagnetism compete with each but paramagnetism in large g region. The main purpose other. For electrons whose Lande-factor g = 2, the zero- of this paper is to calculate the critical value of g. We field paramagnetic susceptibility is two times stronger also present a comparison with results of charged spin-1 than the diamagnetic susceptibility, so the free electron Bose gases which have been obtained previously[12]. gas exhibits paramagnetism altogether. Magnetic properties of relativistic Fermi gases have II. THE MODEL also been under extensive investigation. Daicic et al. developed statistical mechanics for the magnetized pair- fermion gases and found that the intrinsic spin causes We consider a charged Fermi gas of N particles, with important effects upon the relativistic para- and dia- the effective Hamiltonian written as magnetism[2]. H¯ µN = D (ǫ + ǫ µ) n , (1) − L jkz σ − jkz σ The study of ultracold atoms has stimulated renewed j,kXz,σ research interest in the magnetism of quantum gases[3– where µ is the chemical potential and ǫ is the quan- 6]. When atomic gases are confined in optical traps[3, 4], jkz tized Landau energy in the magnetic field B, their spin degree of freedom becomes active, leading to the manifestation of magnetism. Theoretically, the 1 ~2k2 ǫ = ( + j)~ω + z (2) paramagnetism[7] and ferromagnetism[8–10] in a neutral jkz 2 2m∗ spin-1 Bose gas have ever been studied. In experiments, with j = 0, 1, 2,... labeling different Landau levels and 87 magnetic domains have been directly observed in Rb ω = qB/(m∗c) being the gyromagnetic frequency of a ∗ condensate, a typical ferromagnetic spinor condensate[5]. fermion with charge q and mass m . DL = qBSxy/(2π~c) Very recently, the exploration of magnetism in quantum marks the degeneracy of each Landau level with Sxy the arXiv:1006.5179v1 [cond-mat.stat-mech] 27 Jun 2010 gases has been extended to the Fermi gas. It is already total section area in x, y directions of the system. ǫσ observed that an ultracold two-component Fermi gas of denotes the Zeeman energy, neutral 6Li atoms exhibits ferromagnetism caused by re- ~q pulsive interactions between atoms[6]. ~ ǫσ = g ∗ σB = gσ ω, (3) Furthermore, it is possible to realize charged quantum − m c − gases from neutral ultracold atoms. So far, cold plasma where g is the Lande-factor and σ refers to the spin-z index of Zeeman state F, σ . has been created by photoionization of cold atoms[11]. | i The temperatures of electrons and ions are as low as 100 The grand thermodynamic potential of the Fermi gas is expressed as 1 −β(ǫjk +ǫσ−µ) ΩT =06 = DL ln[1 + e z ], (4) ∗ −β Corresponding author: [email protected] j,kXz ,σ 2 −1 0.50 where β = (kBT ) . Performing Taylor expansions and (a) then integrating out kz, Eq. (4) becomes ωV m∗ 3/2 Ω = T =06 2 0.00 − ~ 2πβ M ∞ 3 ~ω ~ ( 1)l+1l− 2 e−lβ( 2 −gσ ω−µ) − , (5) × 1 e−lβ~ω Xl=1 Xσ − -0.50 where V is the volume of the system. For simplicity, the (b) following notation is introduced, 0.80 ∞ p l+1 α/2 −lx(ησ+δ) σ ( 1) l e Fτ [α, δ]= − , (6) M (1 e−lx)τ 0.40 Xl=1 − ~ ~ ~ where x = β ω and η = ( ω/2 µ + ǫ )/( ω). Then σ − σ Eq. (5) is rewritten as 0.00 (c) ∗ 3/2 ωV m -0.44 Ω = F σ[ 3, 0]. (7) T =06 ~2 1 − 2πβ − d Xσ M For a system with the given particle density n = N/V , the chemical potential is obtained according to the fol- -0.48 lowing equation ∗ 3/2 0.0 0.4 0.8 1 ∂Ω m σ n = = x 2 F1 [ 1, 0]. (8) −V ∂µ 2πβ~ − g T,V Xσ A similar treatment has been employed to study diamag- FIG. 1: (a) The total magnetization density (M), (b) the netism of the charged spinless Bose gas[13] and extended paramagnetization density (M p), and (c) the diamagnetiza- to the study of competition of diamagnetism and param- tion density (M d) as a function of g at t = 0.2. The dotted agnetism in charged spin-1 Bose gases[12]. This method and dashed lines correspond to ω = 5 and 10, respectively. is more applicable at relatively high temperatures. To determine gc, we need calculate the magnetization and density M as a function of the magnetic field B and tem- perature T . The system is paramagnetic when M > 0 3/2 σ 1 M 6 =t F [ 3, 0]+ x(gσ ) while diamagnetic when M < 0. M can be derived from T =0 1 − − 2 Xσ the thermodynamic potential by the standard procedure 1 ∂Ω M 6 = , which yields σ σ T =0 − V ∂B T,V F1 [ 1, 0] xF2 [ 1, 1] . (11) × − − − ~ ∗ 3/2 q m σ In following discussions, ω is used to indicate the magni- M 6 = F [ 3, 0] T =0 m∗c 2πβ~2 1 − tude of magnetic field since it is proportional to B. Xσ 1 + x(gσ )F σ[ 1, 0] xF σ[ 1, 1] . (9) − 2 1 − − 2 − III. RESULTS AND DISCUSSIONS For carrying out numerical calculations, it is useful 1 First, we look at a spin- 2 Fermi gas, setting σ = 1 to make the parameters dimensionless, such as M = to present the two Zeeman levels. The dimensionless± ∗ ~ ~ ∗ ∗ ∗ m cM/(n q), ω = ω/(kBT ), and t = T/T . Here T magnetization density M as a function of g is shown in is the characteristic temperature of the system, which is 2 Fig. 1(a). As expected, M is negative in the small g ∗ 2 ∗ given by kB T = 2π~ n 3 /m . Then we have x = ω/t, ′ ′ ∗ region, which means that the diamagnetism dominates. ησ =1/2 µ /ω gσ and µ = µ/(kBT ) in the notation For each given value of ω, M grows with g and changes σ − − Fτ [α, δ]. Equations (8) and (9) can be re-expressed as its sign from negative to positive in the larger g region, indicating that the paramagnetic effect is enhanced due 1= ωt1/2 F σ[ 1, 0] (10) to increase of g. This phenomenon is also observed in the 1 − Xσ Bose system[12]. gc is just the value of g where M = 0. 3 0.50 = 10 0.49 0.45 0.42 = 5 c c g g = 20 0.40 = 10 0.35 = 5 0.28 0.35 0 5 10 15 20 0 5 10 15 20 1/t 1/t FIG. 2: Plots of the critical value of g-factor as a function of FIG. 3: The gc 1/t curves for charged spin-1 gases obey- 1/t. The magnetic field is chosen as ω = 20 (solid line), 10 ing the Bose-Einstein− (BE, dotted line), Maxwell-Boltzmann (dashed line) and 5 (dotted line), respectively. (MB, solid line) and Fermi-Dirac (FD, dashed line) statistics, respectively. The magnetic field is chosen as ω = 10 and 5. The total magnetization M shown in Fig. 1(a) con- 1 1 sists of both the paramagnetic and diamagnetic contri- where λ = hβ 2 /(2πm∗) 2 , z = eβ(µ−ǫσ) and the Fermi- butions. Figure 1(b) depicts the pure paramagnetic con- Dirac integral fn(z) is normally defined as tribution to M, which is calculated by M p = gm where m = n n− . Figure 1(c) plots the diamagnetic con- ∞ n−1 1 − 1 1 x tribution to M, M d = M M p. For each fixed value fn(z) −1 x dx, (14) − ≡ Γ(n) Z0 z e +1 of ω, the diamagnetization M d is slightly weakened with increasing g.
Load more

Recommended publications
  • Solid State Physics 2 Lecture 5: Electron Liquid
    Physics 7450: Solid State Physics 2 Lecture 5: Electron liquid Leo Radzihovsky (Dated: 10 March, 2015) Abstract In these lectures, we will study itinerate electron liquid, namely metals. We will begin by re- viewing properties of noninteracting electron gas, developing its Greens functions, analyzing its thermodynamics, Pauli paramagnetism and Landau diamagnetism. We will recall how its thermo- dynamics is qualitatively distinct from that of a Boltzmann and Bose gases. As emphasized by Sommerfeld (1928), these qualitative di↵erence are due to the Pauli principle of electons’ fermionic statistics. We will then include e↵ects of Coulomb interaction, treating it in Hartree and Hartree- Fock approximation, computing the ground state energy and screening. We will then study itinerate Stoner ferromagnetism as well as various response functions, such as compressibility and conduc- tivity, and screening (Thomas-Fermi, Debye). We will then discuss Landau Fermi-liquid theory, which will allow us understand why despite strong electron-electron interactions, nevertheless much of the phenomenology of a Fermi gas extends to a Fermi liquid. We will conclude with discussion of electrons on the lattice, treated within the Hubbard and t-J models and will study transition to a Mott insulator and magnetism 1 I. INTRODUCTION A. Outline electron gas ground state and excitations • thermodynamics • Pauli paramagnetism • Landau diamagnetism • Hartree-Fock theory of interactions: ground state energy • Stoner ferromagnetic instability • response functions • Landau Fermi-liquid theory • electrons on the lattice: Hubbard and t-J models • Mott insulators and magnetism • B. Background In these lectures, we will study itinerate electron liquid, namely metals. In principle a fully quantum mechanical, strongly Coulomb-interacting description is required.
    [Show full text]
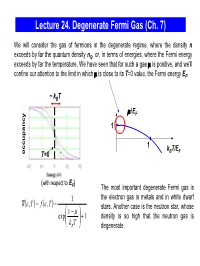
  • Lecture 24. Degenerate Fermi Gas (Ch
    Lecture 24. Degenerate Fermi Gas (Ch. 7) We will consider the gas of fermions in the degenerate regime, where the density n exceeds by far the quantum density nQ, or, in terms of energies, where the Fermi energy exceeds by far the temperature. We have seen that for such a gas μ is positive, and we’ll confine our attention to the limit in which μ is close to its T=0 value, the Fermi energy EF. ~ kBT μ/EF 1 1 kBT/EF occupancy T=0 (with respect to E ) F The most important degenerate Fermi gas is 1 the electron gas in metals and in white dwarf nε()(),, T= f ε T = stars. Another case is the neutron star, whose ε⎛ − μ⎞ exp⎜ ⎟ +1 density is so high that the neutron gas is ⎝kB T⎠ degenerate. Degenerate Fermi Gas in Metals empty states ε We consider the mobile electrons in the conduction EF conduction band which can participate in the charge transport. The band energy is measured from the bottom of the conduction 0 band. When the metal atoms are brought together, valence their outer electrons break away and can move freely band through the solid. In good metals with the concentration ~ 1 electron/ion, the density of electrons in the electron states electron states conduction band n ~ 1 electron per (0.2 nm)3 ~ 1029 in an isolated in metal electrons/m3 . atom The electrons are prevented from escaping from the metal by the net Coulomb attraction to the positive ions; the energy required for an electron to escape (the work function) is typically a few eV.
    [Show full text]
  • Chapter 13 Ideal Fermi
    Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k T µ,βµ 1, B � � which defines the degenerate Fermi gas. In this limit, the quantum mechanical nature of the system becomes especially important, and the system has little to do with the classical ideal gas. Since this chapter is devoted to fermions, we shall omit in the following the subscript ( ) that we used for the fermionic statistical quantities in the previous chapter. − 13.1 Equation of state Consider a gas ofN non-interacting fermions, e.g., electrons, whose one-particle wave- functionsϕ r(�r) are plane-waves. In this case, a complete set of quantum numbersr is given, for instance, by the three cartesian components of the wave vector �k and thez spin projectionm s of an electron: r (k , k , k , m ). ≡ x y z s Spin-independent Hamiltonians. We will consider only spin independent Hamiltonian operator of the type ˆ 3 H= �k ck† ck + d r V(r)c r†cr , �k � where thefirst and the second terms are respectively the kinetic and th potential energy. The summation over the statesr (whenever it has to be performed) can then be reduced to the summation over states with different wavevectork(p=¯hk): ... (2s + 1) ..., ⇒ r � �k where the summation over the spin quantum numberm s = s, s+1, . , s has been taken into account by the prefactor (2s + 1). − − 159 160 CHAPTER 13. IDEAL FERMI GAS Wavefunctions in a box. We as- sume that the electrons are in a vol- ume defined by a cube with sidesL x, Ly,L z and volumeV=L xLyLz.
    [Show full text]
  • Electron-Electron Interactions(Pdf)
    Contents 2 Electron-electron interactions 1 2.1 Mean field theory (Hartree-Fock) ................ 3 2.1.1 Validity of Hartree-Fock theory .................. 6 2.1.2 Problem with Hartree-Fock theory ................ 9 2.2 Screening ..................................... 10 2.2.1 Elementary treatment ......................... 10 2.2.2 Kubo formula ............................... 15 2.2.3 Correlation functions .......................... 18 2.2.4 Dielectric constant ............................ 19 2.2.5 Lindhard function ............................ 21 2.2.6 Thomas-Fermi theory ......................... 24 2.2.7 Friedel oscillations ............................ 25 2.2.8 Plasmons ................................... 27 2.3 Fermi liquid theory ............................ 30 2.3.1 Particles and holes ............................ 31 2.3.2 Energy of quasiparticles. ....................... 36 2.3.3 Residual quasiparticle interactions ................ 38 2.3.4 Local energy of a quasiparticle ................... 42 2.3.5 Thermodynamic properties ..................... 44 2.3.6 Quasiparticle relaxation time and transport properties. 46 2.3.7 Effective mass m∗ of quasiparticles ................ 50 0 Reading: 1. Ch. 17, Ashcroft & Mermin 2. Chs. 5& 6, Kittel 3. For a more detailed discussion of Fermi liquid theory, see G. Baym and C. Pethick, Landau Fermi-Liquid Theory : Concepts and Ap- plications, Wiley 1991 2 Electron-electron interactions The electronic structure theory of metals, developed in the 1930’s by Bloch, Bethe, Wilson and others, assumes that electron-electron interac- tions can be neglected, and that solid-state physics consists of computing and filling the electronic bands based on knowldege of crystal symmetry and atomic valence. To a remarkably large extent, this works. In simple compounds, whether a system is an insulator or a metal can be deter- mined reliably by determining the band filling in a noninteracting cal- culation.
    [Show full text]
  • Schedule for Rest of Quarter • Review: 3D Free Electron Gas • Heat Capacity
    Lecture 16 Housekeeping: schedule for rest of quarter Review: 3D free electron gas Heat capacity of free electron gas Semi classical treatment of electric conductivity Review: 3D fee electron gas This model ignores the lattice and only treats the electrons in a metal. It assumes that electrons do not interact with each other except for pauli exclusion. 풌∙풓 Wavelike-electrons defined by their momentum eigenstate k: 휓풌(풓) = 푒 Treat electrons like quantum particle in a box: confined to a 3D box of dimensions L in every direction Periodic boundary conditions on wavefunction: 휓(푥 + 퐿, 푦, 푧) = 휓(푥, 푦, 푧) 휓(푥, 푦 + 퐿, 푧) = 휓(푥, 푦, 푧) 휓(푥, 푦, 푧 + 퐿) = 휓(푥, 푦, 푧) Permissible values of k of the form: 2휋 4휋 푘 = 0, ± , ± , … 푥 퐿 퐿 Free electron schrodinger’s eqn in 3D + boundary conditions gives energy eigenvalues: ℏ2 휕2 휕2 휕2 − ( + + ) 휓 (푟) = 휖 휓 (푟) 2푚 휕푥2 휕푦2 휕푧2 푘 푘 푘 ℏ2 ℏ2푘2 (푘2 + 푘2 + 푘2) = 휖 = 2푚 푥 푦 푧 푘 2푚 There are N electrons and we put them into available eigenstates following these rules: o Every state is defined by a unique quantized value of (푘푥, 푘푦, 푘푧) o Every state can hold one spin up and one spin down electron o Assume that single-electron solution above applies to collection of electrons (i.e. electrons do not interact and change the eigenstates) o Fill low energy states first. In 3D, this corresponds to filling up a sphere in k space, one 2 2 2 2 ‘shell’ at a time.
    [Show full text]
  • Chapter 6 Free Electron Fermi
    Chapter 6 Free Electron Fermi Gas Free electron model: • The valence electrons of the constituent atoms become conduction electrons and move about freely through the volume of the metal. • The simplest metals are the alkali metals– lithium, sodium, potassium, Na, cesium, and rubidium. • The classical theory had several conspicuous successes, notably the derivation of the form of Ohm’s law and the relation between the electrical and thermal conductivity. • The classical theory fails to explain the heat capacity and the magnetic susceptibility of the conduction electrons. M = B • Why the electrons in a metal can move so freely without much deflections? (a) A conduction electron is not deflected by ion cores arranged on a periodic lattice, because matter waves propagate freely in a periodic structure. (b) A conduction electron is scattered only infrequently by other conduction electrons. Pauli exclusion principle. Free Electron Fermi Gas: a gas of free electrons subject to the Pauli Principle ELECTRON GAS MODEL IN METALS Valence electrons form the electron gas eZa -e(Za-Z) -eZ Figure 1.1 (a) Schematic picture of an isolated atom (not to scale). (b) In a metal the nucleus and ion core retain their configuration in the free atom, but the valence electrons leave the atom to form the electron gas. 3.66A 0.98A Na : simple metal In a sea of conduction of electrons Core ~ occupy about 15% in total volume of crystal Classical Theory (Drude Model) Drude Model, 1900AD, after Thompson’s discovery of electrons in 1897 Based on the concept of kinetic theory of neutral dilute ideal gas Apply to the dense electrons in metals by the free electron gas picture Classical Statistical Mechanics: Boltzmann Maxwell Distribution The number of electrons per unit volume with velocity in the range du about u 3/2 2 fB(u) = n (m/ 2pkBT) exp (-mu /2kBT) Success: Failure: (1) The Ohm’s Law , (1) Heat capacity Cv~ 3/2 NKB the electrical conductivity The observed heat capacity is only 0.01, J = E , = n e2 / m, too small.
    [Show full text]
  • Fermi and Bose Gases
    Fermi and Bose gases Anders Malthe-Sørenssen 25. november 2013 1 1 Thermodynamic identities and Legendre transforms 2 Fermi-Dirac and Bose-Einstein distribution When we discussed the ideal gas we assumed that quantum effects were not important. This was implied when we introduced the term 1=N! for the partition function for the ideal gas, because this term only was valid in the limit when the number of states are many compared to the number of particles. Now, we will address the general case. We start from an individual particle. For a single particle, we address its orbitals: Its possible quantum states, each of which corresponds to a solution of the Schrodinger equation for a single particle. For many particles we will address how the “fill up" the various orbitals { where the underlying assump- tion is that we can treat a many-particle system as a system with the same energy levels as for a single particular system, that is as a system with no interactions between the states of the various particles. However, the number of particles that can occupy the same state depends on the type of particle: For Fermions (1/2 spin) Only 0 or 1 fermion can be in a particular state. For Bosons (integer spin) Any number of bosons can be in a particular state. We will now apply a Gibbs ensemble approach to study this system. This means that we will consider a system where µ, V; T is constant. We can use the Gibbs sum formalism to address the behavior of this system.
    [Show full text]
  • One-Dimensional Multicomponent Fermions with Δ-Function Interaction in Strong- and Weak-Coupling Limits: Κ-Component Fermi Gas
    PHYSICAL REVIEW A 85, 033633 (2012) One-dimensional multicomponent fermions with δ-function interaction in strong- and weak-coupling limits: κ-component Fermi gas Xi-Wen Guan,1 Zhong-Qi Ma,2 and Brendan Wilson1 1Department of Theoretical Physics, Research School of Physics and Engineering, Australian National University, Canberra ACT 0200, Australia 2Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China (Received 23 January 2012; published 26 March 2012) We derive the first few terms of the asymptotic expansion of the Fredholm equations for one-dimensional κ- component fermions with repulsive and attractive δ-function interaction in strong- and weak-coupling regimes. We thus obtain a highly accurate result for the ground-state energy of a multicomponent Fermi gas with polarization for these regimes. This result provides a unified description of the ground-state properties of the Fermi gas with higher spin symmetries. However, in contrast to the two-component Fermi gas, there does not exist a mapping that can unify the two sets of Fredholm equations as the interacting strength vanishes. Moreover, we find that the local pair-correlation functions shed light on the quantum statistic effects of the κ-component interacting fermions. For the balanced spin case with repulsive interaction, the ground-state energy obtained confirms Yang and You’s result [Chin. Phys. Lett. 28, 020503 (2011)] that the energy per particle as κ →∞is the same as for spinless Bosons. DOI: 10.1103/PhysRevA.85.033633 PACS number(s): 03.75.Ss, 03.75.Hh, 02.30.Ik, 34.10.+x I. INTRODUCTION Although the model was solved long ago by Sutherland [4], solutions of the Fredholm equations for the model are far from The recently established experimental control over the being thoroughly investigated except for the two-component effective spin-spin interaction between atoms is opening up Fermi gas [16].
    [Show full text]
  • Ideal Quantum Gases from Statistical Physics Using Mathematica © James J
    Ideal Quantum Gases from Statistical Physics using Mathematica © James J. Kelly, 1996-2002 The indistinguishability of identical particles has profound effects at low temperatures and/or high density where quantum mechanical wave packets overlap appreciably. The occupation representation is used to study the statistical mechanics and thermodynamics of ideal quantum gases satisfying Fermi- Dirac or Bose-Einstein statistics. This notebook concentrates on formal and conceptual developments, liberally quoting more technical results obtained in the auxiliary notebooks occupy.nb, which presents numerical methods for relating the chemical potential to density, and fermi.nb and bose.nb, which study the mathematical properties of special functions defined for Ferm-Dirac and Bose-Einstein systems. The auxiliary notebooks also contain a large number of exercises. Indistinguishability In classical mechanics identical particles remain distinguishable because it is possible, at least in principle, to label them according to their trajectories. Once the initial position and momentum is determined for each particle with the infinite precision available to classical mechanics, the swarm of classical phase points moves along trajectories which also can in principle be determined with absolute certainty. Hence, the identity of the particle at any classical phase point is connected by deterministic relationships to any initial condition and need not ever be confused with the label attached to another trajectory. Therefore, in classical mechanics even identical particles are distinguishable, in principle, even though we must admit that it is virtually impossible in practice to integrate the equations of motion for a many-body system with sufficient accuracy. Conversely, in quantum mechanics identical particles are absolutely indistinguishable from one another.
    [Show full text]
  • 8.044 Lecture Notes Chapter 9: Quantum Ideal Gases
    8.044 Lecture Notes Chapter 9: Quantum Ideal Gases Lecturer: McGreevy 9.1 Range of validity of classical ideal gas . 9-2 9.2 Quantum systems with many indistinguishable particles . 9-4 9.3 Statistical mechanics of N non-interacting (indistinguishable) bosons or fermions 9-9 9.4 Classical ideal gas limit of quantum ideal gas . 9-13 2 9.5 Ultra-high temperature (kBT mc and kBT µ) limit . 9-15 9.6 Fermions at low temperatures . 9-18 9.7 Bosons at low temperatures . 9-33 Reading: Baierlein, Chapters 8 and 9. 9-1 9.1 Range of validity of classical ideal gas For a classical ideal gas, we derived the partition function N 3=2 Z1 V 2πmkBT Z = ;Z1 = 3 = V 2 ; N! λth h h where the length scale λth ≡ is determined by the particle mass and the temperature. 2πmkB T When does this break down? 1. If `idealness' fails, i.e. if interactions become important. This is interesting and impor- tant but out of bounds for 8.044. We'll still assume non-interacting particles. 2. If `classicalness' fails. Even with no interactions, at low enough temperatures, or high enough densities, quantum effects modify Z. An argument that classicalness must fail comes by thinking harder about λth, the \thermal de Broglie wavelength". Why is it called that? Recall from 8.04 that the de Broglie wavelength h for a particle with momentum p is λdB = p . For a classical ideal gas, we know the RMS momentum from equipartition ~p2 3 p h i = k T =) p ≡ ph~p2i = 3mk T: 2m 2 B RMS B We could have defined ~ h h λth ≡ = p ; pRMS 3mkBT there's no significance to the numerical prefactor of p1 instead of p1 .
    [Show full text]
  • Density of States
    Density of States Franz Utermohlen February 13, 2018 Contents 1 Preface 1 2 Summation definition 2 2.1 Examples of Eqs. 2 and 3 for a fermionic system . 2 2.2 Example: Ideal Fermi gas . 3 3 Derivative definition 4 3.1 Example: Ideal Fermi gas . 4 4 Useful expressions 6 1 Preface In these notes, the expressions Vd denotes the volume of a d-dimensional sphere of radius R and Ωd−1 denotes the solid angle a d-dimensional sphere (or equivalently, the surface area of a d-dimensional sphere of unit radius).1 These expressions are given by d=2 d=2 π d 2π Vd = d R ; Ωd−1 = d : (1) Γ(1 + 2 ) Γ( 2 ) For example, for d = 1; 2; and 3, these are d = 1 : V1 = 2R; Ω0 = 2 ; 2 d = 2 : V2 = πR ; Ω1 = 2π ; 4 d = 3 : V = πR3 ; Ω = 4π : 3 3 2 1The d − 1 subscript refers to the fact that the fact that the surface area of a d-dimensional sphere is (d − 1)-dimensional. It's also useful to use d − 1 as the subscript, since the surface area of a d-dimensional d−1 sphere of radius R is given by Sd−1 = Ωd−1R . 1 2 Summation definition Intensive quantities A can generally be expressed in the form 1 X A = a( ) ; (2) V i d i where Vd is the d-dimensional volume of the system, the sum is over all possible single- particle states i, and i is the energy of the single-particle state i.
    [Show full text]
  • §6 – Free Electron Gas : §6 – Free Electron Gas
    §6 – Free Electron Gas : §6 – Free Electron Gas 6.1 Overview of Electronic Properties The main species of solids are metals, semiconductors and insulators. One way to group these is by their resistivity: Metals – ~10−8−10−5 m Semiconductors – ~10−5−10 m Insulators – ~10−∞ m There is a striking difference in the temperature dependence of the resistivity: Metals – ρ increases with T (usually ∝T ) Semiconductors – ρ decreases with T Alloys have higher resistivity than its constituents; there is no law of mixing. This suggests some form of “impurity” mechanism The different species also have different optical properties. Metals – Opaque and lustrous (silvery) Insulators – often transparent or coloured The reasons for these differing properties can be explained by considering the density of electron states: 6.2 Free Electron (Fermi) Gas The simplest model of a metal was proposed by Fermi. This model transfers the ideas of electron orbitals in atoms into a macroscopic object. Thus, the fundamental behaviour of a metal comes from the Pauli exclusion principle. For now, we will ignore the crystal lattice. – 1 – Last Modified: 28/12/2006 §6 – Free Electron Gas : For this model, we make the following assumptions: ● The crystal comprises a fixed background of N identical positively charge nuclei and N electrons, which can move freely inside the crystal without seeing any of the nuclei (monovalent case); ● Coulomb interactions are negligible because the system is neutral overall This model works relatively well for alkali metals (Group 1 elements), such as Na, K, Rb and Cs. We would like to understand why electrons are only weakly scattered as they migrate through a metal.
    [Show full text]