DOCSLIB.ORG

FREE ELECTRON FERMI GAS Outlines Free Electron Gas Electron Free

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
FREE ELECTRON FERMI GAS Outlines Free Electron Gas Electron Free 3/21/2017 3/20/2017 FREE ELECTRON FERMI GAS Outlines Free ElectronGas 1. Energy levels in one dimension 2. Effect of temp on the Fermi-Dirac function 3. Free electron gas in 3D 4. Heat capacity of the electron gas 5. Thermal conductivity of metal Physics UCF 2 In this unit, we study electrons in solid, in particular Inside a real metal, the electron in the conduction band electrons inside a metal. There are some overlap between this unit and unit#1, where we study the Drude model. 1. Will interact with other electron. (correlation, exchange) 3/20/2017 2. Will interact with the atomic potential (Coulomb force) 3/20/2017 In a simple metal, the atom at each lattice site usually has both core electrons and valence electrons. The core Free ElectronGas Free ElectronGas electrons are very similar to those electrons in a free When we ignore atom. However, the valence electrons are quite different from the outer electrons of the free atom. 1. >>>>>>>> Independent electron model 2. >>>>>>>> Free electron model Of course, we can also treat electrons as classical particles or as quantum particles. In this unit, we will examine the success and the failure of this model, and 3 try to understand why. 4 Electron Energy Levels in one dimension One dimensional infinite square well For a particle in a 1D box, the boundary conditions are Let’s consider a free electron gas in one dimension. WE 3/20/2017 ; . The solution can be found 3/20/2017 take into account the fact that electrons are quantum particles satisfy the Schrodinger equation, Free ElectronGas (3) Free ElectronGas (1) where is the wave-function of the electron, is where & Hamiltonian operator and is the eigenvalue of the Hamiltonian operator. Substitute (3) into (1) we obtain (2) (4) In this unit, we are dealing with free electrons, so the 5 6 potential is zero. 1 3/21/2017 So you can see from the figure below the first few energy For each of the energy levels associated with a quantum levels and the wavefunctions look like. number n, there can have only two electrons. For N electrons, the last filled level will be , and we define Since this is a one dimensional solid, so only one principle 3/20/2017 3/20/2017 quantum number n, but electron has an intrinsic Fermi energy as the energy of the topmost filled level in the quantum number called spin. So for 1D electron gas, ground state of the N electron system. there are two degree of freedom. Now electrons are Free ElectronGas Free ElectronGas fermions so they satisfy the Fermi-Dirac distribution. (5) For 6 electrons in a 1D infinite square well the ground state is given by: The Fermi-Dirac Distribution n Occupancy 1 ↑ 1 The Fermi-Dirac distribution gives the probability that an 1 ↓ 1 orbital at energy will be occupied in an ideal electron gas 2 ↑ 1 at thermal equilibrium 2 ↓ 1 3 ↑ 1 (6) 7 / 8 3 ↓ 1 4 ↑ 0 Free electron gas in 3D The free electron in 3D satisfies the Schrodinger eq. 3/20/2017 3/20/2017 (7) Free ElectronGas Free ElectronGas The solution is · (8) , , ,⋯ , , ,⋯ The quantity µ is a function of temperature. At , . At other temperature, is equal to ½ when , , ,⋯ 9 10 . The energy of the system is given by The total number of electrons is just (volume density) (9) · · 3/20/2017 3/20/2017 In the reciprocal space, as the states are occupied by N electrons, when ≫, the occupied states form a sphere Free ElectronGas (11) Free ElectronGas The surface of this sphere is Substitute back into Eq. (10), we end up with called Fermi surface and the energy at the surface at T=0 (12) is called Fermi energy. The electron velocity at the Fermi surface is given by (10) (13) 11 12 2 3/21/2017 Re-arrange Eq. (12), we express N in terms of If we assume each electron occupies a volume of , (14) where is the Wigner-Seitz radius, 3/20/2017 3/20/2017 The density of states is · · (15) Free ElectronGas Free ElectronGas ≡ · · · · ≅. (16) 13 14 For free electron, the band structure is dominated by Heat capacity of the electron gas parabolic function since One of the early difficulties encountered in the Drude model was the experimental heat capacity of the electron gas was 3/20/2017 much smaller than that expected from the classic model. 3/20/2017 (17) Classical theory Free ElectronGas Each electron in 3D has energy, so the heat capacity Free ElectronGas is Experimental data showed %of The answer to this question was given by Fermi through the Fermi- Dirac distribution of 15 Fermion. 16 At temp T only a fraction of all electrons been excited , Quantitative calculation of The energy required to raise the temperature by 1 °C is 3/20/2017 3/20/2017 · · (18) ·· ·· (20) Free ElectronGas Free ElectronGas ~ ~ (19) ·· (21) At room temperature, Since · · (22) % 17 18 Combine Eq. (21) and (22), 3 3/21/2017 In 1D or 2D electron gas model, For ≪ 3/20/2017 3/20/2017 (23) Experimental heat capacity / Free ElectronGas At temperature below Debye temp and Fermi temp, the Free ElectronGas (24) heat capacity of metals can be written as the sum of / electron and lattice contributions (Eq. 15-1(#6) & eq. 26) / (25) (27) / (26) 19 20 The departure from simple free electron model come from From Eq. (26) we can see that (1) interaction with atomic potential, (2) interaction with phonon, (3) interaction with other electrons. (28) 3/20/2017 3/20/2017 Take into account Eq. (12) & (15), we can see that Free ElectronGas Free ElectronGas is proportional to the mass of the electron. Since experimental measurement of is typically different from the simple , so we usually redefine the mass of electron to force fit the equation (28), we can the fitted mass as effective mass, (29) 21 22 Thermal conductivity of metals Wiedemann-Franz Law At moderate temperature, the ratio between and σ In Drude model, the thermal conductivity K is expressed as depends on T linearly, the factor is called Lorentz number, L 3/20/2017 3/20/2017 (30) / Free ElectronGas (31) Free ElectronGas At low T, the head capacity dominated by the electronic / contribution, therefore we can substitute (26) into (30) ·· (31) 23 24 4.
Load more

Recommended publications
  • Fermi- Dirac Statistics
    Prof. Surajit Dhara Guest Teacher, Dept. Of Physics, Narajole Raj College GE2T (Thermal physics and Statistical Mechanics) , Topic :- Fermi- Dirac Statistics Fermi- Dirac Statistics Basic features: The basic features of the Fermi-Dirac statistics: 1. The particles are all identical and hence indistinguishable. 2. The fermions obey (a) the Heisenberg’s uncertainty relation and also (b) the exclusion principle of Pauli. 3. As a consequence of 2(a), there exists a number of quantum states for a given energy level and because of 2(b) , there is a definite a priori restriction on the number of fermions in a quantum state; there can be simultaneously no more than one particle in a quantum state which would either remain empty or can at best contain one fermion. If , again, the particles are isolated and non-interacting, the following two additional condition equations apply to the system: ∑ ; Thermodynamic probability: Consider an isolated system of N indistinguishable, non-interacting particles obeying Pauli’s exclusion principle. Let particles in the system have energies respectively and let denote the degeneracy . So the number of distinguishable arrangements of particles among eigenstates in the ith energy level is …..(1) Therefore, the thermodynamic probability W, that is, the total number of s eigenstates of the whole system is the product of ……(2) GE2T (Thermal physics and Statistical Mechanics), Topic :- Fermi- Dirac Statistics: Circulated by-Prof. Surajit Dhara, Dept. Of Physics, Narajole Raj College FD- distribution function : Most probable distribution : From eqn(2) above , taking logarithm and applying Stirling’s theorem, For this distribution to represent the most probable distribution , the entropy S or klnW must be maximum, i.e.
    [Show full text]
  • Solid State Physics II Level 4 Semester 1 Course Content
    Solid State Physics II Level 4 Semester 1 Course Content L1. Introduction to solid state physics - The free electron theory : Free levels in one dimension. L2. Free electron gas in three dimensions. L3. Electrical conductivity – Motion in magnetic field- Wiedemann-Franz law. L4. Nearly free electron model - origin of the energy band. L5. Bloch functions - Kronig Penney model. L6. Dielectrics I : Polarization in dielectrics L7 .Dielectrics II: Types of polarization - dielectric constant L8. Assessment L9. Experimental determination of dielectric constant L10. Ferroelectrics (1) : Ferroelectric crystals L11. Ferroelectrics (2): Piezoelectricity L12. Piezoelectricity Applications L1 : Solid State Physics Solid state physics is the study of rigid matter, or solids, ,through methods such as quantum mechanics, crystallography, electromagnetism and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from their atomic- scale properties. Thus, solid-state physics forms the theoretical basis of materials science. It also has direct applications, for example in the technology of transistors and semiconductors. Crystalline solids & Amorphous solids Solid materials are formed from densely-packed atoms, which interact intensely. These interactions produce : the mechanical (e.g. hardness and elasticity), thermal, electrical, magnetic and optical properties of solids. Depending on the material involved and the conditions in which it was formed , the atoms may be arranged in a regular, geometric pattern (crystalline solids, which include metals and ordinary water ice) , or irregularly (an amorphous solid such as common window glass). Crystalline solids & Amorphous solids The bulk of solid-state physics theory and research is focused on crystals.
    [Show full text]
  • Competition Between Paramagnetism and Diamagnetism in Charged
    Competition between paramagnetism and diamagnetism in charged Fermi gases Xiaoling Jian, Jihong Qin, and Qiang Gu∗ Department of Physics, University of Science and Technology Beijing, Beijing 100083, China (Dated: November 10, 2018) The charged Fermi gas with a small Lande-factor g is expected to be diamagnetic, while that with a larger g could be paramagnetic. We calculate the critical value of the g-factor which separates the dia- and para-magnetic regions. In the weak-field limit, gc has the same value both at high and low temperatures, gc = 1/√12. Nevertheless, gc increases with the temperature reducing in finite magnetic fields. We also compare the gc value of Fermi gases with those of Boltzmann and Bose gases, supposing the particle has three Zeeman levels σ = 1, 0, and find that gc of Bose and Fermi gases is larger and smaller than that of Boltzmann gases,± respectively. PACS numbers: 05.30.Fk, 51.60.+a, 75.10.Lp, 75.20.-g I. INTRODUCTION mK and 10 µK, respectively. The ions can be regarded as charged Bose or Fermi gases. Once the quantum gas Magnetism of electron gases has been considerably has both the spin and charge degrees of freedom, there studied in condensed matter physics. In magnetic field, arises the competition between paramagnetism and dia- the magnetization of a free electron gas consists of two magnetism, as in electrons. Different from electrons, the independent parts. The spin magnetic moment of elec- g-factor for different magnetic ions is diverse, ranging trons results in the paramagnetic part (the Pauli para- from 0 to 2.
    [Show full text]
  • Solid State Physics 2 Lecture 5: Electron Liquid
    Physics 7450: Solid State Physics 2 Lecture 5: Electron liquid Leo Radzihovsky (Dated: 10 March, 2015) Abstract In these lectures, we will study itinerate electron liquid, namely metals. We will begin by re- viewing properties of noninteracting electron gas, developing its Greens functions, analyzing its thermodynamics, Pauli paramagnetism and Landau diamagnetism. We will recall how its thermo- dynamics is qualitatively distinct from that of a Boltzmann and Bose gases. As emphasized by Sommerfeld (1928), these qualitative di↵erence are due to the Pauli principle of electons’ fermionic statistics. We will then include e↵ects of Coulomb interaction, treating it in Hartree and Hartree- Fock approximation, computing the ground state energy and screening. We will then study itinerate Stoner ferromagnetism as well as various response functions, such as compressibility and conduc- tivity, and screening (Thomas-Fermi, Debye). We will then discuss Landau Fermi-liquid theory, which will allow us understand why despite strong electron-electron interactions, nevertheless much of the phenomenology of a Fermi gas extends to a Fermi liquid. We will conclude with discussion of electrons on the lattice, treated within the Hubbard and t-J models and will study transition to a Mott insulator and magnetism 1 I. INTRODUCTION A. Outline electron gas ground state and excitations • thermodynamics • Pauli paramagnetism • Landau diamagnetism • Hartree-Fock theory of interactions: ground state energy • Stoner ferromagnetic instability • response functions • Landau Fermi-liquid theory • electrons on the lattice: Hubbard and t-J models • Mott insulators and magnetism • B. Background In these lectures, we will study itinerate electron liquid, namely metals. In principle a fully quantum mechanical, strongly Coulomb-interacting description is required.
    [Show full text]
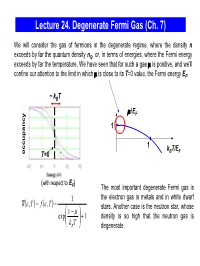
  • Lecture 24. Degenerate Fermi Gas (Ch
    Lecture 24. Degenerate Fermi Gas (Ch. 7) We will consider the gas of fermions in the degenerate regime, where the density n exceeds by far the quantum density nQ, or, in terms of energies, where the Fermi energy exceeds by far the temperature. We have seen that for such a gas μ is positive, and we’ll confine our attention to the limit in which μ is close to its T=0 value, the Fermi energy EF. ~ kBT μ/EF 1 1 kBT/EF occupancy T=0 (with respect to E ) F The most important degenerate Fermi gas is 1 the electron gas in metals and in white dwarf nε()(),, T= f ε T = stars. Another case is the neutron star, whose ε⎛ − μ⎞ exp⎜ ⎟ +1 density is so high that the neutron gas is ⎝kB T⎠ degenerate. Degenerate Fermi Gas in Metals empty states ε We consider the mobile electrons in the conduction EF conduction band which can participate in the charge transport. The band energy is measured from the bottom of the conduction 0 band. When the metal atoms are brought together, valence their outer electrons break away and can move freely band through the solid. In good metals with the concentration ~ 1 electron/ion, the density of electrons in the electron states electron states conduction band n ~ 1 electron per (0.2 nm)3 ~ 1029 in an isolated in metal electrons/m3 . atom The electrons are prevented from escaping from the metal by the net Coulomb attraction to the positive ions; the energy required for an electron to escape (the work function) is typically a few eV.
    [Show full text]
  • Chapter 13 Ideal Fermi
    Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k T µ,βµ 1, B � � which defines the degenerate Fermi gas. In this limit, the quantum mechanical nature of the system becomes especially important, and the system has little to do with the classical ideal gas. Since this chapter is devoted to fermions, we shall omit in the following the subscript ( ) that we used for the fermionic statistical quantities in the previous chapter. − 13.1 Equation of state Consider a gas ofN non-interacting fermions, e.g., electrons, whose one-particle wave- functionsϕ r(�r) are plane-waves. In this case, a complete set of quantum numbersr is given, for instance, by the three cartesian components of the wave vector �k and thez spin projectionm s of an electron: r (k , k , k , m ). ≡ x y z s Spin-independent Hamiltonians. We will consider only spin independent Hamiltonian operator of the type ˆ 3 H= �k ck† ck + d r V(r)c r†cr , �k � where thefirst and the second terms are respectively the kinetic and th potential energy. The summation over the statesr (whenever it has to be performed) can then be reduced to the summation over states with different wavevectork(p=¯hk): ... (2s + 1) ..., ⇒ r � �k where the summation over the spin quantum numberm s = s, s+1, . , s has been taken into account by the prefactor (2s + 1). − − 159 160 CHAPTER 13. IDEAL FERMI GAS Wavefunctions in a box. We as- sume that the electrons are in a vol- ume defined by a cube with sidesL x, Ly,L z and volumeV=L xLyLz.
    [Show full text]
  • Inorganic Chemistry for Dummies® Published by John Wiley & Sons, Inc
    Inorganic Chemistry Inorganic Chemistry by Michael L. Matson and Alvin W. Orbaek Inorganic Chemistry For Dummies® Published by John Wiley & Sons, Inc. 111 River St. Hoboken, NJ 07030-5774 www.wiley.com Copyright © 2013 by John Wiley & Sons, Inc., Hoboken, New Jersey Published by John Wiley & Sons, Inc., Hoboken, New Jersey Published simultaneously in Canada No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permis- sion of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley. com/go/permissions. Trademarks: Wiley, the Wiley logo, For Dummies, the Dummies Man logo, A Reference for the Rest of Us!, The Dummies Way, Dummies Daily, The Fun and Easy Way, Dummies.com, Making Everything Easier, and related trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates in the United States and other countries, and may not be used without written permission. All other trade- marks are the property of their respective owners. John Wiley & Sons, Inc., is not associated with any product or vendor mentioned in this book.
    [Show full text]
  • Chapter 6 Free Electron Fermi Gas
    理学院 物理系 沈嵘 Chapter 6 Free Electron Fermi Gas 6.1 Electron Gas Model and its Ground State 6.2 Thermal Properties of Electron Gas 6.3 Free Electrons in Electric Fields 6.4 Hall Effect 6.5 Thermal Conductivity of Metals 6.6 Failures of the free electron gas model 1 6.1 Electron Gas Model and its Ground State 6.1 Electron Gas Model and its Ground State I. Basic Assumptions of Electron Gas Model Metal: valence electrons → conduction electrons (moving freely) ü The simplest metals are the alkali metals—lithium, sodium, 2 potassium, cesium, and rubidium. 6.1 Electron Gas Model and its Ground State density of electrons: Zr n = N m A A where Z is # of conduction electrons per atom, A is relative atomic mass, rm is the density of mass in the metal. The spherical volume of each electron is, 1 3 1 V 4 3 æ 3 ö = = p rs rs = ç ÷ n N 3 è 4p nø Free electron gas model: Suppose, except the confining potential near surfaces of metals, conduction electrons are completely free. The conduction electrons thus behave just like gas atoms in an ideal gas --- free electron gas. 3 6.1 Electron Gas Model and its Ground State Basic Properties： ü Ignore interactions of electron-ion type (free electron approx.) ü And electron-eletron type (independent electron approx). Total energy are of kinetic type, ignore potential energy contribution. ü The classical theory had several conspicuous successes 4 6.1 Electron Gas Model and its Ground State Long Mean Free Path: ü From many types of experiments it is clear that a conduction electron in a metal can move freely in a straight path over many atomic distances.
    [Show full text]
  • Electron-Electron Interactions(Pdf)
    Contents 2 Electron-electron interactions 1 2.1 Mean field theory (Hartree-Fock) ................ 3 2.1.1 Validity of Hartree-Fock theory .................. 6 2.1.2 Problem with Hartree-Fock theory ................ 9 2.2 Screening ..................................... 10 2.2.1 Elementary treatment ......................... 10 2.2.2 Kubo formula ............................... 15 2.2.3 Correlation functions .......................... 18 2.2.4 Dielectric constant ............................ 19 2.2.5 Lindhard function ............................ 21 2.2.6 Thomas-Fermi theory ......................... 24 2.2.7 Friedel oscillations ............................ 25 2.2.8 Plasmons ................................... 27 2.3 Fermi liquid theory ............................ 30 2.3.1 Particles and holes ............................ 31 2.3.2 Energy of quasiparticles. ....................... 36 2.3.3 Residual quasiparticle interactions ................ 38 2.3.4 Local energy of a quasiparticle ................... 42 2.3.5 Thermodynamic properties ..................... 44 2.3.6 Quasiparticle relaxation time and transport properties. 46 2.3.7 Effective mass m∗ of quasiparticles ................ 50 0 Reading: 1. Ch. 17, Ashcroft & Mermin 2. Chs. 5& 6, Kittel 3. For a more detailed discussion of Fermi liquid theory, see G. Baym and C. Pethick, Landau Fermi-Liquid Theory : Concepts and Ap- plications, Wiley 1991 2 Electron-electron interactions The electronic structure theory of metals, developed in the 1930’s by Bloch, Bethe, Wilson and others, assumes that electron-electron interac- tions can be neglected, and that solid-state physics consists of computing and filling the electronic bands based on knowldege of crystal symmetry and atomic valence. To a remarkably large extent, this works. In simple compounds, whether a system is an insulator or a metal can be deter- mined reliably by determining the band filling in a noninteracting cal- culation.
    [Show full text]
  • Schedule for Rest of Quarter • Review: 3D Free Electron Gas • Heat Capacity
    Lecture 16 Housekeeping: schedule for rest of quarter Review: 3D free electron gas Heat capacity of free electron gas Semi classical treatment of electric conductivity Review: 3D fee electron gas This model ignores the lattice and only treats the electrons in a metal. It assumes that electrons do not interact with each other except for pauli exclusion. 풌∙풓 Wavelike-electrons defined by their momentum eigenstate k: 휓풌(풓) = 푒 Treat electrons like quantum particle in a box: confined to a 3D box of dimensions L in every direction Periodic boundary conditions on wavefunction: 휓(푥 + 퐿, 푦, 푧) = 휓(푥, 푦, 푧) 휓(푥, 푦 + 퐿, 푧) = 휓(푥, 푦, 푧) 휓(푥, 푦, 푧 + 퐿) = 휓(푥, 푦, 푧) Permissible values of k of the form: 2휋 4휋 푘 = 0, ± , ± , … 푥 퐿 퐿 Free electron schrodinger’s eqn in 3D + boundary conditions gives energy eigenvalues: ℏ2 휕2 휕2 휕2 − ( + + ) 휓 (푟) = 휖 휓 (푟) 2푚 휕푥2 휕푦2 휕푧2 푘 푘 푘 ℏ2 ℏ2푘2 (푘2 + 푘2 + 푘2) = 휖 = 2푚 푥 푦 푧 푘 2푚 There are N electrons and we put them into available eigenstates following these rules: o Every state is defined by a unique quantized value of (푘푥, 푘푦, 푘푧) o Every state can hold one spin up and one spin down electron o Assume that single-electron solution above applies to collection of electrons (i.e. electrons do not interact and change the eigenstates) o Fill low energy states first. In 3D, this corresponds to filling up a sphere in k space, one 2 2 2 2 ‘shell’ at a time.
    [Show full text]
  • Chapter 6 Free Electron Fermi
    Chapter 6 Free Electron Fermi Gas Free electron model: • The valence electrons of the constituent atoms become conduction electrons and move about freely through the volume of the metal. • The simplest metals are the alkali metals– lithium, sodium, potassium, Na, cesium, and rubidium. • The classical theory had several conspicuous successes, notably the derivation of the form of Ohm’s law and the relation between the electrical and thermal conductivity. • The classical theory fails to explain the heat capacity and the magnetic susceptibility of the conduction electrons. M = B • Why the electrons in a metal can move so freely without much deflections? (a) A conduction electron is not deflected by ion cores arranged on a periodic lattice, because matter waves propagate freely in a periodic structure. (b) A conduction electron is scattered only infrequently by other conduction electrons. Pauli exclusion principle. Free Electron Fermi Gas: a gas of free electrons subject to the Pauli Principle ELECTRON GAS MODEL IN METALS Valence electrons form the electron gas eZa -e(Za-Z) -eZ Figure 1.1 (a) Schematic picture of an isolated atom (not to scale). (b) In a metal the nucleus and ion core retain their configuration in the free atom, but the valence electrons leave the atom to form the electron gas. 3.66A 0.98A Na : simple metal In a sea of conduction of electrons Core ~ occupy about 15% in total volume of crystal Classical Theory (Drude Model) Drude Model, 1900AD, after Thompson’s discovery of electrons in 1897 Based on the concept of kinetic theory of neutral dilute ideal gas Apply to the dense electrons in metals by the free electron gas picture Classical Statistical Mechanics: Boltzmann Maxwell Distribution The number of electrons per unit volume with velocity in the range du about u 3/2 2 fB(u) = n (m/ 2pkBT) exp (-mu /2kBT) Success: Failure: (1) The Ohm’s Law , (1) Heat capacity Cv~ 3/2 NKB the electrical conductivity The observed heat capacity is only 0.01, J = E , = n e2 / m, too small.
    [Show full text]
  • Fermi and Bose Gases
    Fermi and Bose gases Anders Malthe-Sørenssen 25. november 2013 1 1 Thermodynamic identities and Legendre transforms 2 Fermi-Dirac and Bose-Einstein distribution When we discussed the ideal gas we assumed that quantum effects were not important. This was implied when we introduced the term 1=N! for the partition function for the ideal gas, because this term only was valid in the limit when the number of states are many compared to the number of particles. Now, we will address the general case. We start from an individual particle. For a single particle, we address its orbitals: Its possible quantum states, each of which corresponds to a solution of the Schrodinger equation for a single particle. For many particles we will address how the “fill up" the various orbitals { where the underlying assump- tion is that we can treat a many-particle system as a system with the same energy levels as for a single particular system, that is as a system with no interactions between the states of the various particles. However, the number of particles that can occupy the same state depends on the type of particle: For Fermions (1/2 spin) Only 0 or 1 fermion can be in a particular state. For Bosons (integer spin) Any number of bosons can be in a particular state. We will now apply a Gibbs ensemble approach to study this system. This means that we will consider a system where µ, V; T is constant. We can use the Gibbs sum formalism to address the behavior of this system.
    [Show full text]