DOCSLIB.ORG

Molecular Mechanics Studies of Enzyme Evolutionary Mechanisms Manoj Singh Clemson University, [email protected]

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Molecular Mechanics Studies of Enzyme Evolutionary Mechanisms Manoj Singh Clemson University, Mksingh@Clemson.Edu Clemson University TigerPrints All Dissertations Dissertations 1-2010 Molecular Mechanics Studies of Enzyme Evolutionary Mechanisms Manoj Singh Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_dissertations Part of the Chemistry Commons Recommended Citation Singh, Manoj, "Molecular Mechanics Studies of Enzyme Evolutionary Mechanisms" (2010). All Dissertations. 680. https://tigerprints.clemson.edu/all_dissertations/680 This Dissertation is brought to you for free and open access by the Dissertations at TigerPrints. It has been accepted for inclusion in All Dissertations by an authorized administrator of TigerPrints. For more information, please contact [email protected]. ABSTRACT In the current dissertation, closely related studies to quantify the mechanism underlying enzyme evolution have been discussed. The HIV-1 protease and !-lactamase enzymes were used as model systems for these studies. These are well known enzymes that are associated with drug resistance and are associated with the pathogenic diseases, and therefore, developing molecular level understanding of drug resistance through these enzymes has fundamental as well as practical importance. In chapter 2, the relationship between errors in modeled protein structures and associated binding affinity predictions to small molecules is established. The results of this study are applicable in addressing a wide range of biological questions including enzyme evolutionary mechanisms. The next three chapters discuss different aspects of HIV-1 protease evolution. In chapter 3, the role of substrate binding in manipulating the catalytic activity of HIV-1 protease during evolution has been examined. The results suggest that HIV-1 protease can optimize its catalytic activity by manipulating its substrate binding affinity. This part of study also emphasizes the importance of considering the in-vivo environment while studying physical-chemical aspects of enzymatic evolution. In chapter 4, the role of dynamics as a constraint on the evolution of HIV-1 protease has been examined. Low frequency motions (dynamics) of an enzyme have been suggested to be critical for its function. It has been further suggested that any mutation that disrupts these low frequency motions may have an adverse affect on the catalytic function of the enzyme. In this part of study, the role of dynamics as a constraint on the evolution of HIV-1 protease has been examined by comparing experimental ii activity data for over 90 mutants of HIV-1 protease to correlated motion data obtained from molecular dynamics simulations of a Michaelis complex. The results of this study suggest that dynamics do not impose a significant constraint on the evolution of HIV-1 protease. In chapter 5, the role of fold stability as a constraint on the evolution of HIV-1 protease is examined. A significant tradeoff between evolvability and fold stability for HIV-1 protease was observed in our study. The results of this study suggest that fold stability imposes a significant constraint on the evolution of HIV-1 protease, and in future attempts to predict evolutionary outcomes (drug resistant mutations), fold stability should also be taken into consideration. In chapter 6, the evolution of cefotaximase activity within !-lactamase is described. !-lactamase is a bacterial enzyme that catalytically hydrolyzes the !-lactam antibiotic, and therefore inactivates these drugs. Five point mutations are, however, required in the gene of this enzyme in order to develop cefotaximase activity. In this part of our study, we have studied the effect of four drug resistant amino acid mutations [A42G, E104K, G238S, and M182T] on the structural properties and cefotaximase activity of !-lactamase. Along with the successful identification of evolutionary beneficial mutations, our analyses suggest structural rearrangement within active site as a possible mechanism for increasing the activity against cefotaxime. iii DEDICATION To my family. iv ACKNOWLEDGMENTS I would like to thank, first of all, my advisor Prof. Brian Dominy. He has not only given me opportunity to pursue my PhD in the area of my interest, but has also been a wonderful mentor throughout my studies. I remember knocking his door countless number of times and he was always available for discussion and advice. He has taught me much more than science. I would also like to thank my graduate committee members for providing important comments and suggestions that greatly improved this dissertation. I would like to acknowledge Prof. Steve Stuart for his various courses which helped understand computational chemistry during my graduate studies. I am also very thankful to Computing and Information Technology department at Clemson University for installing and maintaining Palmetto cluster. Without this wonderful resource, my studies would have been less exciting. Finally, I would like to thank my family and friends. Without their constant support and encouragement, this journey would have been much more difficult. Manoj Kumar Singh December, 2010 v TABLE OF CONTENTS Page TITLE PAGE....................................................................................................................i ABSTRACT.....................................................................................................................ii DEDICATION................................................................................................................iv ACKNOWLEDGMENTS ...............................................................................................v LIST OF TABLES..........................................................................................................ix LIST OF FIGURES ........................................................................................................xi CHAPTER I. INTRODUCTION .........................................................................................1 II. THERMODYNAMIC RESOLUTION: HOW DO ERRORS IN MODELED PROTEIN STRUCTURES AFFECT BINDING AFFINITY PREDICTIONS?.....................................................................8 Abstract....................................................................................................8 Introduction..............................................................................................9 Methods..................................................................................................11 Results and Discussion ..........................................................................17 vi Table of Contents (Continued) Page Conclusions............................................................................................29 III. THE EVOLUTION OF CATALYTIC FUNCTION IN THE HIV-1 PROTEASE..............................................................................................30 Abstract..................................................................................................30 Introduction............................................................................................32 Theoretical Background of Protease Activity Calculation ....................36 Methods..................................................................................................42 Results and Discussion ..........................................................................50 Conclusions............................................................................................68 IV. ROLE OF DYNAMICS AS A CONSTRAINT ON THE EVOLUTION OF HIV-1 PROTEASE....................................................69 Abstract..................................................................................................69 Introduction............................................................................................71 Methods..................................................................................................75 Results and Discussion ..........................................................................81 Conclusions............................................................................................96 V. ROLE OF FOLD STABILITY AS A CONSTRAINT ON THE EVOLUTION OF HIV-1 PROTEASE....................................................97 Abstract..................................................................................................97 vii Table of Contents (Continued) Page Introduction............................................................................................98 Theoretical Background.......................................................................102 Results..................................................................................................106 Discussion............................................................................................117 Methods................................................................................................119 VI. THE EVOLUTION OF CEFOTAXIMASE ACTIVITY IN THE TEM !-LACTAMASE...........................................................................122 Abstract................................................................................................122 Introduction..........................................................................................124 Methods................................................................................................131 Results..................................................................................................140 Discussion............................................................................................154
Load more

Recommended publications
  • Jacquelyn S. Fetrow
    Jacquelyn S. Fetrow President and Professor of Chemistry Albright College Curriculum Vitae Office of the President Work Email: [email protected] Library and Administration Building Office Phone: 610-921-7600 N. 13th and Bern Streets, P.O. Box 15234 Reading, PA 19612 Education Ph.D. Biological Chemistry, December, 1986 B.S. Biochemistry, May, 1982 Department of Biological Chemistry Albright College, Reading, PA The Pennsylvania State University College of Medicine, Hershey, PA Graduated summa cum laude Loops: A Novel Class of Protein Secondary Structure Thesis Advisor: George D. Rose Professional Experience Albright College, Reading PA President and Professor of Chemistry June 2017-present University of Richmond, Richmond, VA Provost and Vice President of Academic Affairs July 2014-December 2016 Professor of Chemistry July 2014-May 2017 Responsibilities as Provost: Chief academic administrator for all academic matters for the University of Richmond, a university with five schools (Arts and Sciences, Business, Law, Leadership, and Professional and Continuing Studies), ~400 faculty and ~3300 full-time undergraduate and graduate students; manage the ~$91.8M annual operating budget of the Academic Affairs Division, as well as endowment and gift accounts; oversee Richmond’s Bonner Center of Civic Engagement (engage.richmond.edu), Center for International Education (international.richmond.edu), Registrar (registrar.richmond.edu), Office of Institutional Effectiveness (ifx.richmond.edu), as well as other programs and staff; partner with VP
    [Show full text]
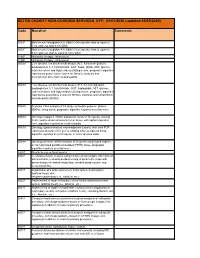
  • SETON CHARITY NON-COVERED SERVICES EFF: 01/01/2020 (Updated 05/05/2020)
    SETON CHARITY NON-COVERED SERVICES EFF: 01/01/2020 (updated 05/05/2020) Code Narrative Comments 3051F Most recent hemoglobin A1c (HbA1c) level greater than or equal to 7.0% and less than 8.0% (DM) 3052F Most recent hemoglobin A1c (HbA1c) level greater than or equal to 8.0% and less than or equal to 9.0% (DM) 4185F Histamine therapy - intravenous 4186F Histamine therapy - intravenous 0002M Liver disease, ten biochemical assays (ALT, A2-macro- globulin, apolipoprotein A-1, total bilirubin, GGT, hapto- globin, AST, glucose, total cholesterol and triglycerides) utilizing serum, prognostic algorithm reported as quanti- tative scores for fibrosis, steatosis and alcoholic/non alco- holic steatohepatitis 0003M Liver disease, ten biochemical assays (ALT, A2-macroglobulin, apolipoprotein A-1, total bilirubin, GGT, haptoglobin, AST, glucose, total cholesterol and triglycerides) utilizing serum, prognostic algorithm reported as quantitative scores for fibrosis, steatosis and nonalcoholic steatohepatitis (NASH) 0004M Scoliosis, DNA analysis of 53 single nucleotide polymor- phisms (SNPs), using saliva, prognostic algorithm reported as a risk score 0006M Oncology (hepatic), mRNA expression levels of 161 genes, utilizing fresh hepatocellular carcinoma tumor tissue, with alpha-fetoprotein level, algorithm reported as a risk classifier 0007M Oncology (gastrointestinal neuroendocrine tumors), real- time PCR expression analysis of 51 genes, utilizing whole peripheral blood, algorithm reported as a nomogram of tumor disease index 0008M Oncology (breast), mRNA
    [Show full text]
  • Genome-Wide Investigation of Cellular Functions for Trna Nucleus
    Genome-wide Investigation of Cellular Functions for tRNA Nucleus- Cytoplasm Trafficking in the Yeast Saccharomyces cerevisiae DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Hui-Yi Chu Graduate Program in Molecular, Cellular and Developmental Biology The Ohio State University 2012 Dissertation Committee: Anita K. Hopper, Advisor Stephen Osmani Kurt Fredrick Jane Jackman Copyright by Hui-Yi Chu 2012 Abstract In eukaryotic cells tRNAs are transcribed in the nucleus and exported to the cytoplasm for their essential role in protein synthesis. This export event was thought to be unidirectional. Surprisingly, several lines of evidence showed that mature cytoplasmic tRNAs shuttle between nucleus and cytoplasm and their distribution is nutrient-dependent. This newly discovered tRNA retrograde process is conserved from yeast to vertebrates. Although how exactly the tRNA nuclear-cytoplasmic trafficking is regulated is still under investigation, previous studies identified several transporters involved in tRNA subcellular dynamics. At least three members of the β-importin family function in tRNA nuclear-cytoplasmic intracellular movement: (1) Los1 functions in both the tRNA primary export and re-export processes; (2) Mtr10, directly or indirectly, is responsible for the constitutive retrograde import of cytoplasmic tRNA to the nucleus; (3) Msn5 functions solely in the re-export process. In this thesis I focus on the physiological role(s) of the tRNA nuclear retrograde pathway. One possibility is that nuclear accumulation of cytoplasmic tRNA serves to modulate translation of particular transcripts. To test this hypothesis, I compared expression profiles from non-translating mRNAs and polyribosome-bound translating mRNAs collected from msn5Δ and mtr10Δ mutants and wild-type cells, in fed or acute amino acid starvation conditions.
    [Show full text]
  • The Development of the Prediction of Protein Structure
    6 The Development of the Prediction of Protein Structure Gerald D. Fasman I. Introduction .................................................................... 194 II. Protein Topology. .. 196 III. Techniques of Protein Prediction ................................................... 198 A. Sequence Alignment .......................................................... 199 B. Hydrophobicity .............................................................. 200 C. Minimum Energy Calculations ................................................. 202 IV. Approaches to Protein Conformation ................................................ 203 A. Solvent Accessibility ......................................................... 203 B. Packing of Residues .......................................................... 204 C. Distance Geometry ........................................................... 205 D. Amino Acid Physicochemical Properties ......................................... 205 V. Prediction of the Secondary Structure of Proteins: a Helix, ~ Strands, and ~ Turn .......... 208 A. ~ Turns .................................................................... 209 B. Evaluation of Predictive Methodologies .......................................... 218 C. Other Predictive Algorithms ................................................... 222 D. Chou-Fasman Algorithm ...................................................... 224 E. Class Prediction ............................................................. 233 VI. Prediction of Tertiary Structure ...................................................
    [Show full text]
  • Cooperative Omega Loops in Cytochrome C: Role in Folding and Function
    doi:10.1016/S0022-2836(03)00697-1 J. Mol. Biol. (2003) 331, 29–36 COMMUNICATION Cooperative Omega Loops in Cytochrome c: Role in Folding and Function Mallela M. G. Krishna*, Yan Lin, Jon N. Rumbley and S. Walter Englander Department of Biochemistry Hydrogen exchange experiments under slow exchange conditions show and Biophysics, Johnson that an omega loop in cytochrome c (residues 40–57) acts as a cooperative Research Foundation unfolding/refolding unit under native conditions. This unit behavior University of Pennsylvania accounts for an initial step on the unfolding pathway, a final step in School of Medicine, 422 Curie refolding, and a number of other structural, functional and evolutionary Blvd, 1007 Stellar Chance Bldg properties. Philadelphia, PA 19104-6059 q 2003 Elsevier Ltd. All rights reserved USA Keywords: omega loop; protein folding; hydrogen exchange; cytochrome c; *Corresponding author protein function Leszczynski and Rose found that a category of state. Under favorable conditions, the otherwise non-regular protein secondary structure, which invisible low level unfolding reactions can be they called the V loop, accounts for 25% of the made to dominate the HX behavior of the amino amino acid residues in protein molecules.1 The acids that they expose. HX results can then identify termini of V loops come close in three-dimensional the major higher energy states and measure their space and their side-chain atoms pack tightly but equilibrium4,5 and kinetic6 parameters. irregularly to produce compact substructures. Previous HX experiments
    [Show full text]
  • How Folding and Binding Free Energies Correlate with Beta-Lactamase Fitness Abstract
    bioRxiv preprint doi: https://doi.org/10.1101/2020.04.15.043661; this version posted April 16, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Predicting the Viability of Beta-Lactamase: How Folding and Binding Free Energies Correlate with Beta-Lactamase Fitness Jordan Yang1, Nandita Naik2, Jagdish Suresh Patel3,4, Christopher S. Wylie2, Wenze Gu1, Jessie Huang5, Marty Ytreberg3,4, Mandar T. Naik6, Daniel M. Weinreich2, and Brenda M. Rubenstein1* 1 Department of Chemistry, Brown University, Providence, Rhode Island, United States of America 2 Department of Ecology and Evolutionary Biology, Brown University, Providence, Rhode Island, United States of America 3 Center for Modeling Complex Interactions, University of Idaho, Moscow, Idaho, United States of America 4 Department of Biological Sciences, University of Idaho, Moscow, Idaho, United States of America 5 Department of Chemistry, Wellesley College, Wellesley, Massachusetts, United States of America 6 Department of Molecular Pharmacology, Physiology, and Biotechnology, Brown University, Providence, Rhode Island, United States of America * brenda [email protected] Abstract One of the long-standing holy grails of molecular evolution has been the ability to predict an organism's fitness directly from its genotype. With such predictive abilities in hand, researchers would be able to more accurately forecast how organisms will evolve and how proteins with novel functions could be engineered, leading to revolutionary advances in medicine and biotechnology. In this work, we assemble the largest reported set of experimental TEM-1 β-lactamase folding free energies and use this data in conjunction with previously acquired fitness data and computational free energy predictions to determine how much of the fitness of β-lactamase can be directly predicted by thermodynamic folding and binding free energies.
    [Show full text]
  • The Role of the O-Loop in Regulation of the Catalytic Activity of TEM-Type Β-Lactamases
    biomolecules Review The Role of the W-Loop in Regulation of the Catalytic Activity of TEM-Type β-Lactamases Alexey Egorov 1,*, Maya Rubtsova 1, Vitaly Grigorenko 1, Igor Uporov 1 and Alexander Veselovsky 2 1 Department Chemistry, M.V. Lomonosov Moscow State University, 3, 1, Leninskie gori, Moscow 119991, Russia; [email protected] (M.R.); [email protected] (V.G.); [email protected] (I.U.) 2 Institute of Biomedical Chemistry, ul. Pogodinskaya 10, Moscow 119121, Russia; [email protected] * Correspondence: [email protected]; Tel.: +7-495-939-2727 Received: 22 October 2019; Accepted: 9 December 2019; Published: 11 December 2019 Abstract: Bacterial resistance to β-lactams, the most commonly used class of antibiotics, poses a global challenge. This resistance is caused by the production of bacterial enzymes that are termed β-lactamases (βLs). The evolution of serine-class A β-lactamases from penicillin-binding proteins (PBPs) is related to the formation of the W-loop at the entrance to the enzyme’s active site. In this loop, the Glu166 residue plays a key role in the two-step catalytic cycle of hydrolysis. This residue in TEM–type β-lactamases, together with Asn170, is involved in the formation of a hydrogen bonding network with a water molecule, leading to the deacylation of the acyl–enzyme complex and the hydrolysis of the β-lactam ring of the antibiotic. The activity exhibited by the W-loop is attributed to the positioning of its N-terminal residues near the catalytically important residues of the active site. The structure of the W-loop of TEM-type β-lactamases is characterized by low mutability, a stable topology, and structural flexibility.
    [Show full text]
  • Local Protein Structures Bernard Offmann, Manoj Tyagi, Alexandre De Brevern
    Local Protein Structures Bernard Offmann, Manoj Tyagi, Alexandre de Brevern To cite this version: Bernard Offmann, Manoj Tyagi, Alexandre de Brevern. Local Protein Structures. Current Bioinfor- matics, Benthams Science, 2007, 2, pp.165-202. inserm-00175058 HAL Id: inserm-00175058 https://www.hal.inserm.fr/inserm-00175058 Submitted on 11 May 2010 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. HAL authorLocal manuscript Protein Structures (Offmann, Tyagi & de Brevern) Current Bioinformatics 2007;2:165-202 Preprint for Current Bioinformatics 2007 HAL author manuscript inserm-00175058, version 1 Local Protein Structures Offmann B. 1, Tyagi M. 1+ & de Brevern A.G. 2* 1 Laboratoire de Biochimie et Génétique Moléculaire, Université de La Réunion, 15, avenue René Cassin, BP7151, 97715 Saint Denis Messag Cedex 09, La Réunion, France 2 Equipe de Bioinformatique Génomique et Moléculaire (EBGM), INSERM UMR-S 726, Université Paris Diderot, case 7113, 2, place Jussieu, 75251 Paris, France * Corresponding author: mailing address: Dr. de Brevern A.G., Equipe de Bioinformatique Génomique et Moléculaire (EBGM), INSERM UMR-S 726, Université Paris Diderot, case 7113, 2, place Jussieu, 75251 Paris, France E-mail : [email protected] Tel: (33) 1 44 27 77 31 Fax: (33) 1 43 26 38 30 key words: secondary structure, protein folds, structure-sequence relationship, structural alphabet, protein blocks, molecular modeling, ab initio .
    [Show full text]
  • The Drug-Resistant Variant P167S Expands the Substrate Profile Of
    Lawrence Berkeley National Laboratory Recent Work Title The Drug-Resistant Variant P167S Expands the Substrate Profile of CTX-M β-Lactamases for Oxyimino-Cephalosporin Antibiotics by Enlarging the Active Site upon Acylation. Permalink https://escholarship.org/uc/item/8d39c004 Journal Biochemistry, 56(27) ISSN 0006-2960 Authors Patel, Meha P Hu, Liya Stojanoski, Vlatko et al. Publication Date 2017-07-01 DOI 10.1021/acs.biochem.7b00176 Peer reviewed eScholarship.org Powered by the California Digital Library University of California HHS Public Access Author manuscript Author ManuscriptAuthor Manuscript Author Biochemistry Manuscript Author . Author manuscript; Manuscript Author available in PMC 2017 October 17. Published in final edited form as: Biochemistry. 2017 July 11; 56(27): 3443–3453. doi:10.1021/acs.biochem.7b00176. The Drug-Resistant Variant P167S Expands the Substrate Profile of CTX-M β-lactamases for Oxyimino-Cephalosporin Antibiotics by Enlarging the Active Site upon Acylation Meha P. Patel1,3, Liya Hu2, Vlatko Stojanoski2,3, Banumathi Sankaran4, B. V. Venkataram Prasad2, and Timothy Palzkill1,2,3,* 1Interdepartmental Graduate Program in Translational Biology and Molecular Medicine, Baylor College of Medicine, Houston, TX 77030 2Verna Marrs McLean Department of Biochemistry and Molecular Biology, Baylor College of Medicine, Houston, TX 77030 3Department of Pharmacology, Baylor College of Medicine, Houston, TX 77030 4Department of Molecular Biophysics and Integrated Bioimaging, Berkeley Center for Structural Biology, Lawrence Berkeley National Laboratory, Berkeley, California 94720 Abstract β-Lactamases are enzymes produced by bacterial cells that provide resistance to β-lactam antibiotics. The CTX-M class of β-lactamases provides resistance against the antibiotic, cefotaxime, but not a related oxyimino-cephalosporin antibiotic, ceftazidime.
    [Show full text]
  • Lactamase Harboring the M169L Clinical Mutation
    The Journal of Antibiotics (2016) 69, 858–862 & 2016 Japan Antibiotics Research Association All rights reserved 0021-8820/16 www.nature.com/ja ORIGINAL ARTICLE Kinetic characterization of GES-22 β-lactamase harboring the M169L clinical mutation Aysegul Saral1,2, David A Leonard3, Azer Ozad Duzgun4, Aysegul Copur Cicek5, Cynthia M June3 and Cemal Sandalli2 The class A β-lactamase GES-22 has been identified in Acinetobacter baumannii isolates in Turkey, and subsequently shown to differ from GES-11 by a single substitution (M169L). Because M169 is part of the omega loop, a structure that is known to have major effects on substrate selectivity in class A β-lactamases, we expressed, purified and kinetically characterized this novel variant. Our results show that compared with GES-116×His, GES-226×His displays more efficient hydrolysis of penicillins, and aztreonam, but a loss of efficiency against ceftazidime. In addition, the M169L substitution confers on GES-22 more efficient hydrolysis of the mechanistic inhibitors clavulanic acid and sulbactam. These effects are highly similar to other mutations at the homologous position in other class A β-lactamases, suggesting that this methionine has a key structural role in aligning active site residues and in substrate selectivity across the class. The Journal of Antibiotics (2016) 69, 858–862; doi:10.1038/ja.2016.48; published online 11 May 2016 INTRODUCTION The origin of GES-type β-lactamases remains unknown, but β-Lactamases are bacterial enzymes that hydrolyze β-lactam they generally are found in class 1 integron gene cassettes on both antibiotics, rendering these compounds ineffective.1 These enzymes chromosomes and plasmids.7 The first GES β-lactamase, GES-1, are grouped into four classes A, B, C and D, with class A, C and D was described in France in 2000.8 This enzyme confers resistance enzymes making use of a catalytic serine to hydrolyze the β-lactam to penicillins, narrow- and expanded-spectrum cephalosporins ring, and class B enzymes using a metal cofactor (Zn).
    [Show full text]
  • 267817312.Pdf
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by RERO DOC Digital Library Published in "Antimicrobial Agents and Chemotherapy doi: 10.1128/AAC.01111-19, 2019" which should be cited to refer to this work. Phenotypic, Biochemical, and Genetic Analysis of KPC-41, a KPC-3 Variant Conferring Resistance to Ceftazidime-Avibactam and Exhibiting Reduced Carbapenemase Activity Linda Mueller,a,b,c Amandine Masseron,a Guy Prod’Hom,c Tatiana Galperine,d Gilbert Greub,c Laurent Poirel,a,b,e Patrice Nordmanna,b,c,e aEmerging Antibiotic Resistance Unit, Medical and Molecular Microbiology, Faculty of Science and Medicine, University of Fribourg, Fribourg, Switzerland bSwiss National Reference Center for Emerging Antibiotic Resistance (NARA), University of Fribourg, Fribourg, Switzerland cInstitut for Microbiology, University Hospital Center and University of Lausanne, Lausanne, Switzerland dInfectiology Department, University Hospital Center and University of Lausanne, Lausanne, Switzerland eINSERM European Unit (IAME, France), University of Fribourg, Fribourg, Switzerland ABSTRACT A novel KPC variant, KPC-41, was identified in a Klebsiella pneumoniae clinical isolate from Switzerland. This ␤-lactamase possessed a 3-amino-acid insertion (Pro-Asn-Lys) located between amino acids 269 and 270 compared to the KPC-3 amino acid sequence. Cloning and expression of the blaKPC-41 gene in Escherichia coli, followed by determination of MIC values and kinetic parameters, showed that KPC-41, compared to those of KPC-3, has an increased affinity to ceftazidime and a decreased sensitivity to avibactam, leading to resistance to ceftazidime-avibactam once produced in K. pneumoniae. Furthermore, KPC-41 exhibited a drastic decrease of its carbapenemase activity.
    [Show full text]
  • The Role of Protein Loops and Linkers in Conformational Dynamics and Allostery
    The role of protein loops and linkers in conformational dynamics and allostery Elena Papaleo1,2*, Giorgio Saladino3, Matteo Lambrughi4, Kresten Lindorff-Larsen2, Francesco Luigi Gervasio3, Ruth Nussinov5,6 1 Computational Biology Laboratory, Unit of Statistics, Bioinformatics and Registry, Danish Cancer Society Research Center, Strandboulevarden 49, 2100, Copenhagen, Denmark 2 Structural Biology and NMR Laboratory, Department of Biology, University of Copenhagen, Copenhagen, Denmark 3 Department of Chemistry, University College London, London, U.K. 4 Department of Biotechnology and Biosciences, University of Milano-Bicocca, Piazza della Scienza 2, 20126, Milan, Italy 5 Cancer and Inflammation Program, Leidos Biomedical Research, Inc. Frederick National Laboratory for Cancer Research, National Cancer Institute Frederick, MD 21702 6 Sackler Institute of Molecular Medicine, Department of Human Genetics and Molecular Medicine Sackler School of Medicine, Tel Aviv University, Tel Aviv 69978, Israel * Corresponding author: Elena Papaleo, [email protected] Abstract Proteins are dynamic entities that undergo a plethora of conformational changes that may take place on a wide range of length- and time-scales. These changes can be as small as the rotation of one or a few side chain dihedral angles or involve concerted motions in larger portions of the three-dimensional structure; both kinds of motions can be important for biological function and allostery. It is becoming increasingly evident that “connector regions” are important components of the dynamic personality of protein structures. These regions may either be disordered loops, i.e. poorly structured regions connecting secondary structural elements, or linkers that connect entire protein domains. Experimental and computational studies have, however, revealed that these regions are not mere connectors, and their role in allostery and conformational changes has been emerging in the last decades.
    [Show full text]