Numerical Solution of Partial Differential Equation Finite Random Grids
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Honour Killing in Sindh Men's and Women's Divergent Accounts
Honour Killing in Sindh Men's and Women's Divergent Accounts Shahnaz Begum Laghari PhD University of York Women’s Studies March 2016 Abstract The aim of this project is to investigate the phenomenon of honour-related violence, the most extreme form of which is honour killing. The research was conducted in Sindh (one of the four provinces of Pakistan). The main research question is, ‘Are these killings for honour?’ This study was inspired by a need to investigate whether the practice of honour killing in Sindh is still guided by the norm of honour or whether other elements have come to the fore. It is comprised of the experiences of those involved in honour killings through informal, semi- structured, open-ended, in-depth interviews, conducted under the framework of the qualitative method. The aim of my thesis is to apply a feminist perspective in interpreting the data to explore the tradition of honour killing and to let the versions of the affected people be heard. In my research, the women who are accused as karis, having very little redress, are uncertain about their lives; they speak and reveal the motives behind the allegations and killings in the name of honour. The male killers, whom I met inside and outside the jails, justify their act of killing in the name of honour, culture, tradition and religion. Drawing upon interviews with thirteen women and thirteen men, I explore and interpret the data to reveal their childhood, educational, financial and social conditions and the impacts of these on their lives, thoughts and actions. -
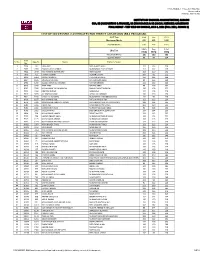
Announced on Monday, July 19, 2021
FINAL RESULT - FALL 2021 ROUND 2 Announced on Monday, July 19, 2021 INSTITUTE OF BUSINESS ADMINISTRATION, KARACHI BBA, BS (ACCOUNTING & FINANCE), BS (ECONOMICS) & BS (SOCIAL SCIENCES) ADMISSIONS FINAL RESULT ‐ TEST HELD ON SUNDAY, JULY 4, 2021 (FALL 2021, ROUND 2) LIST OF SUCCESSFUL CANDIDATES FOR DIRECT ADMISSION (BBA PROGRAM) SAT Test Math Eng TOTAL Maximum Marks 800 800 1600 Cut-Off Marks 600 600 1420 Math Eng Total IBA Test MCQ MCQ MCQ Maximum Marks 180 180 360 Cut-Off Marks 88 88 224 Seat S. No. App No. Name Father's Name No. 1 7904 30 LAIBA RAZI RAZI AHMED JALALI 112 116 228 2 7957 2959 HASSAAN RAZA CHINOY MUHAMMAD RAZA CHINOY 112 132 244 3 7962 3549 MUHAMMAD SHAYAN ARIF ARIF HUSSAIN 152 120 272 4 7979 455 FATIMA RIZWAN RIZWAN SATTAR 160 92 252 5 8000 1464 MOOSA SHERGILL FARZAND SHERGILL 124 124 248 6 8937 1195 ANAUSHEY BATOOL ATTA HUSSAIN SHAH 92 156 248 7 8938 1200 BIZZAL FARHAN ALI MEMON FARHAN MEMON 112 112 224 8 8978 2248 AFRA ABRO NAVEED ABRO 96 136 232 9 8982 2306 MUHAMMAD TALHA MEMON SHAHID PARVEZ MEMON 136 136 272 10 9003 3266 NIRDOSH KUMAR NARAIN NA 120 108 228 11 9017 3635 ALI SHAZ KARMANI IMTIAZ ALI KARMANI 136 100 236 12 9031 1945 SAIFULLAH SOOMRO MUHAMMAD IBRAHIM SOOMRO 132 96 228 13 9469 1187 MUHAMMAD ADIL RAFIQ AHMAD KHAN 112 112 224 14 9579 2321 MOHAMMAD ABDULLAH KUNDI MOHAMMAD ASGHAR KHAN KUNDI 100 124 224 15 9582 2346 ADINA ASIF MALIK MOHAMMAD ASIF 104 120 224 16 9586 2566 SAMAMA BIN ASAD MUHAMMAD ASAD IQBAL 96 128 224 17 9598 2685 SYED ZAFAR ALI SYED SHAUKAT HUSSAIN SHAH 124 104 228 18 9684 526 MUHAMMAD HAMZA -

Public Sector Development Programme (Sectorwise) 2017 - 18 Original
Public Sector Development Programme (Sectorwise) 2017 - 18 Original 06-15-2017 1 of 226 Public Sector Development Programme (Sectorwise) 2017 - 18 Original Chapter: AGRICULTURE Sector: Agriculture Subsector: Agricultural Extension Estimated Cost Exp: Upto June 2017 Fin: Allocation 2017-18 Fin: Thr: Fwd: S No Project ID Project Name GOB / Total GOB / Total Achv: Capital/ Revenue Total Target GOB / FPA FPA FPA % FPA % Ongoing 1 Z2004.0083 CONST: OF MARKET SQUARES 187.881 187.881 159.856 159.856 85% 15.000 0.000 15.000 93% 13.025 Provincial AT LORALAI, K. SAIFULLAH, 0.000 0.000 0.000 0.000 Approved PISHIN, LASBELA, PANJGUR & KHUZDAR. 2 Z2008.0015 MIRANI DAM COMMAND AREA 677.412 677.412 246.000 246.000 36% 50.000 0.000 50.000 43% 381.412 Kech DEVELOPMENT PROJECT 0.000 0.000 0.000 0.000 Approved (PHASE-II) (PHASE-I EXP. 105 MILLION). 3 Z2008.0016 SABAKZAI DAM COMMAND AREA 309.419 309.419 185.500 185.500 59% 50.000 0.000 50.000 76% 73.919 Zhob DEVELOPMENT PROJECT 0.000 0.000 0.000 0.000 Approved (PHASE-II) (PHASE-1 EXP. 119.519 MILLION). 4 Z2013.0072 UPGRADATION OF 4589.397 4589.397 1678.062 1678.062 36% 225.500 0.000 225.500 41% 2685.835 Quetta AGRICULTURE COLLEGE 0.000 0.000 0.000 0.000 Approved QUETTA INTO AGRICULTURE UNIVERSITY BALOCHISTAN AT QUETTA. 5 Z2013.0170 SETTELMENT OF KACHHI AREA. 51.164 51.164 44.894 44.894 87% 6.270 0.000 6.270 100% 0.000 Kachhi 0.000 0.000 0.000 0.000 Approved 6 Z2014.0020 WATER MANAGEMENT 1500.000 1500.000 1483.722 1483.722 98% 16.278 0.000 16.278 100% 0.000 Provincial PROGRAM (WATER COURSES, 0.000 0.000 0.000 0.000 Approved PONDS ETC). -

The Musalman Races Found in Sindh
A SHORT SKETCH, HISTORICAL AND TRADITIONAL, OF THE MUSALMAN RACES FOUND IN SINDH, BALUCHISTAN AND AFGHANISTAN, THEIR GENEALOGICAL SUB-DIVISIONS AND SEPTS, TOGETHER WITH AN ETHNOLOGICAL AND ETHNOGRAPHICAL ACCOUNT, BY SHEIKH SADIK ALÍ SHER ALÍ, ANSÀRI, DEPUTY COLLECTOR IN SINDH. PRINTED AT THE COMMISSIONER’S PRESS. 1901. Reproduced By SANI HUSSAIN PANHWAR September 2010; The Musalman Races; Copyright © www.panhwar.com 1 DEDICATION. To ROBERT GILES, Esquire, MA., OLE., Commissioner in Sindh, This Volume is dedicated, As a humble token of the most sincere feelings of esteem for his private worth and public services, And his most kind and liberal treatment OF THE MUSALMAN LANDHOLDERS IN THE PROVINCE OF SINDH, ВY HIS OLD SUBORDINATE, THE COMPILER. The Musalman Races; Copyright © www.panhwar.com 2 PREFACE. In 1889, while I was Deputy Collector in the Frontier District of Upper Sindh, I was desired by B. Giles, Esquire, then Deputy Commissioner of that district, to prepare a Note on the Baloch and Birahoi tribes, showing their tribal connections and the feuds existing between their various branches, and other details. Accordingly, I prepared a Note on these two tribes and submitted it to him in May 1890. The Note was revised by me at the direction of C. E. S. Steele, Esquire, when he became Deputy Commissioner of the above district, and a copy of it was furnished to him. It was revised a third time in August 1895, and a copy was submitted to H. C. Mules, Esquire, after he took charge of the district, and at my request the revised Note was printed at the Commissioner-in-Sindh’s Press in 1896, and copies of it were supplied to all the District and Divisional officers. -

List of Dehs in Sindh
List of Dehs in Sindh S.No District Taluka Deh's 1 Badin Badin 1 Abri 2 Badin Badin 2 Achh 3 Badin Badin 3 Achhro 4 Badin Badin 4 Akro 5 Badin Badin 5 Aminariro 6 Badin Badin 6 Andhalo 7 Badin Badin 7 Angri 8 Badin Badin 8 Babralo-under sea 9 Badin Badin 9 Badin 10 Badin Badin 10 Baghar 11 Badin Badin 11 Bagreji 12 Badin Badin 12 Bakho Khudi 13 Badin Badin 13 Bandho 14 Badin Badin 14 Bano 15 Badin Badin 15 Behdmi 16 Badin Badin 16 Bhambhki 17 Badin Badin 17 Bhaneri 18 Badin Badin 18 Bidhadi 19 Badin Badin 19 Bijoriro 20 Badin Badin 20 Bokhi 21 Badin Badin 21 Booharki 22 Badin Badin 22 Borandi 23 Badin Badin 23 Buxa 24 Badin Badin 24 Chandhadi 25 Badin Badin 25 Chanesri 26 Badin Badin 26 Charo 27 Badin Badin 27 Cheerandi 28 Badin Badin 28 Chhel 29 Badin Badin 29 Chobandi 30 Badin Badin 30 Chorhadi 31 Badin Badin 31 Chorhalo 32 Badin Badin 32 Daleji 33 Badin Badin 33 Dandhi 34 Badin Badin 34 Daphri 35 Badin Badin 35 Dasti 36 Badin Badin 36 Dhandh 37 Badin Badin 37 Dharan 38 Badin Badin 38 Dheenghar 39 Badin Badin 39 Doonghadi 40 Badin Badin 40 Gabarlo 41 Badin Badin 41 Gad 42 Badin Badin 42 Gagro 43 Badin Badin 43 Ghurbi Page 1 of 142 List of Dehs in Sindh S.No District Taluka Deh's 44 Badin Badin 44 Githo 45 Badin Badin 45 Gujjo 46 Badin Badin 46 Gurho 47 Badin Badin 47 Jakhralo 48 Badin Badin 48 Jakhri 49 Badin Badin 49 janath 50 Badin Badin 50 Janjhli 51 Badin Badin 51 Janki 52 Badin Badin 52 Jhagri 53 Badin Badin 53 Jhalar 54 Badin Badin 54 Jhol khasi 55 Badin Badin 55 Jhurkandi 56 Badin Badin 56 Kadhan 57 Badin Badin 57 Kadi kazia -

Pakistan Engineering Council List of Contractor's Firms in Sindh 2017-18
Pakistan Engineering Council List Of Contractor's Firms in Sindh 2017-18 Sr # Cat Reg # Firm Name Validity City Phone Email 1 C1 5 GREAVES PAKISTAN (PVT) LTD Jun 30, 2018 KARACHI 02135682565-7 [email protected] 2 CA 9 SIEMENS PAKISTAN ENGG CO LTD Jun 30, 2018 KARACHI 3222224645 [email protected] 3 OA 10 PAK OASIS INDUSTRIES (PVT) LTD Jun 30, 2018 KARACHI 2132414319 [email protected] 4 C2 12 PROCON (PVT) LTD Jun 30, 2018 KARACHI 2135840848 [email protected] 5 C3 15 SEASONMASTER ENGINEERING (PVT) LTD. Jun 30, 2018 KARACHI 5396351-3 [email protected]. 6 O2 16 S.D ENTERPRISES Jun 30, 2018 KARACHI 7 CA 22 RAMZAN AND SONS (PVT) LTD Jun 30, 2018 KARACHI 02135821861-62 [email protected] 8 O2 23 GOOD LUCK ENTERPRISES Jun 30, 2018 KARACHI 9 O2 25 DEOKJAE CONSTRUCTION COMPANY (PVT) LTD. Jun 30, 2018 KACHHI 2135860985 [email protected] 10 CA 27 SAITA (PAKISTAN) PTE LTD Jun 30, 2019 KARACHI 021-34548577 saita @cyber.net.pk 11 CB 29 JAMMY CONSTRUCTORS (PVT) LTD Jun 30, 2018 KARACHI 2134551671 [email protected] 12 O3 31 ALLIED ENGINEERING & SERVICES (PVT) LTD Jun 30, 2018 KARACHI 0215066901-13 [email protected]/www.aesl.com.pk 13 C1 36 NAWAB BROTHERS (PVT) LTD Jun 30, 2018 KARACHI 2136724061 [email protected] 14 O1 40 KOHISAR ENTERPRISES Jun 30, 2018 KARACHI 2135685005 [email protected] 15 O3 42 CONTRACT PLUS Jun 30, 2018 KARACHI 3018268003 16 O1 42 ABDUL QAYOOM MAZARI Jun 30, 2018 KASHMORE 3337366688 [email protected] 17 CA 43 USMANI INTERNATIONAL ASSOCIATESPVT LTD Jun 30, 2018 KARACHI 02135653501-3 [email protected] -

2013-2014 Development Budget
1 SC22051(051) DEVELOPMENT (REVENUE) Rs Charged: ______________ Voted: 33,098,087,000 ______________ Total: 33,098,087,000 ______________ ____________________________________________________________________________________________ AGRICULTURE DEPARTMENT ____________________________________________________________________________________________ AGRICULTURE RESEARCH ____________________________________________________________________________________________ P./ADP DDO Functional-Cum-Object Classification & Budget NO. NO. Particular Of Scheme Estimates 2013 - 2014 ____________________________________________________________________________________________ Rs 04 ECONOMIC AFFAIRS 042 AGRI,FOOD,IRRIGATION,FORESTRY & FISHING 0421 AGRICULTURE 042103 AGRICULTURAL RESEARCH & EXTENSION SERVIC HD9337 DIRECTOR GENERAL AGRICULTURE RESEARCH SINDH. ADP No : 0001 HD09100137 Development and Promotion of Quality Seed through Public 134,896,000 Private Partnership in Sindh A03970 Others 134,896,000 TA9384 DY.DIRECTOR RICE RESEARCH STATION THATTA ADP No : 0002 TA12131410 Rehabilitation of Rice & Cotton Research Station Thatta 34,826,000 A03970 Others 34,826,000 KR9613 SECRETARY AGRICULTURE ADP No : 0003 HD12138010 Establishment of Agriculture Services Complex and Advisory 10,520,000 Centers in Sindh A03970 Others 10,520,000 HD9337 DIRECTOR GENERAL AGRICULTURE RESEARCH SINDH. ADP No : 0004 KA11120007 Development of Bio - Pesticide for mangement of vegetable 9,414,000 pests. A03970 Others 9,414,000 LA9404 DIRECTOR QUAID-E-AWAM ARI LARKANA ADP No : 0005 LA11120008 -

Weekly Epidemiological Bulletin Disease Early Warning System and Response in Pakistan
Weekly Bulletin Epidemiological Disease early warning system and response in Pakistan Volume 3, Issue 48, Wednesday 5 December 2012 Highlights Figure‐1: 88 districts reported to DEWS in week 48, 2012 Epidemiological week no. 48 (25 Nov to 1 Dec 2012) • Measles: 122 alerts investigated this week, responding to 31 outbreaks involving 397 measles cases. Vitamin A was provided to cases and EDOs‐H took action to improve vaccination in af‐ fected areas (Page 7) • AWD: 4 alerts investigated this week, involving 9 cases. Alerts/Outbreaks were responded timely and appropri‐ ate measures were taken on case man‐ agement and infection control (Page 7) • 88 districts have reported to DEWS in week 48, 2012. 2,517 health facilities have shared weekly data to the Disease Early Warning System (DEWS) in this Priority diseases Cumulative number of selected health events reported in week under surveillance Epi‐week 1 to 48, 2012 (1 Jan ‐ 1 Dec 2012) in DEWS Pneumonia Disease # of Cases Percentage • 868,251 patients’ consultations were Acute Watery Diarrhoea Bloody diarrhoea Acute diarrhoea 2,988,251 8% reported in week 48 compared to Other Acute Diarrhoea 762,234 consultations reported in Suspected Enteric/Typhoid Fever Bloody diarrhoea 163,653 0.5% week 47, 2012. Suspected Malaria Suspected Meningitis Suspected Dengue fever ARI 6,683,257 19% Suspected Viral Hemorrhagic Fever Suspected Measles S. Malaria 1,878,776 5% • Altogether 204 alerts were investigated Suspected Diphtheria Suspected Pertussis and response were provided to 35 Suspected Acute Viral Hepatitis Skin Diseases 1,628,384 5% outbreaks. Neonatal Tetanus Acute Flaccid Paralysis Unexplained fever 1,277,383 4% Scabies Cutaneous Leishmaniasis Total (All consultations) 35,702,258 Major health events reported during the Figure‐2: Weekly trend of Acute diarrhoea in Pakistan; Week‐1, 2011 to week‐48, 2012. -

Type of Education Facilities in Qambar Shahdadkot
PAKISTAN: Type of education facilities in Qambar Shahdadkot Govt. education facilities "P Primary School Jaffarabad UMED ALI Jacobabad "H JUNEJO High School Jhal "P "M Middle School KOT MUHAMMAD GHULAM NABI BAKHAR Magsi KOT JHURO KHAN BHUTTO BHURIGRI SIYAL "C College CHHATO "P "P "P "P Jamali SANJAR "T Technical institute "P "M BHATTI "V Shahdadkot Vocational AMIR JAN TAJO JEANWAN KHUDA HAYAT KHAN "P MUGHERI LAGHARI LAGHARI BUX GOPANG Balochistan Qubo GOPNAG Roads AHMED SHAHPUR "P "P "P Saeed BROHI JAMALI Aitbar "P KACHI ABDUL Khan "P Khan Primary PUL WAHAB "P QUBO MUHAMMAD Chandio LAL KHAN KOT LAL BUX KHOSO KOT "H SAEED MAZHARUL HASSAN MASTOI "H MAHESAR Secondary SHAHBEG ISLAM AITBAR KHAN MIR SHAH SOBHO KARIRO CHANDIO BHING Sijawal HAJI IIIAHI "H KHAN "P P "P "P GUL HASSAN WASAYO P P "H PUNHAL BUX KHOSO " "P " " CHANDIO Tertiary AASHIQUE "P KOT KHAN MUGHERI NOOR MUHAMMAD"P KAMBAR "M BHATTI JEAND P FAIZ MUHAMMAD JUMO "P LAK ALI M. "P ALI MUGHARI SHAHBEG " "P "P SHAHDADKOT "P "H "P FAZUL MUHAMMAD BROHI BHATTI SOOMRO PUL P SIDDIQI MADARSA LARKANA "P SIJAWAL "P 97000 "M " "P "P DARYA KHAN P Dhingano International Boundary SHAHDADKOT "P "C MITHO " "P MUHAMMAD LARKANA MASTOI KHAN "M Mahesar Shahdadkot 03 P "H "H "P ARZI PUR QAMBRANI P " SHAHDADKOT MASTOI "H " "C CHAKYANI DOLAT JI BHUTTO BUXIO S.KOT Khuzdar "P "P SHAHDADKOT SHAH WANDH SARIO Province Boundary Hazar MIR -JI- "P JO LAO Tharo "P TAR P Wah NARI KARIRA " ALI DOST Wadho MATHION GUL Miro MAGSI "M BHARMEE District Boundary P KALHORO Bagodero NABI BUX MUHAMMAD " MIRO CHAJURI P P CHAKAR -

Prime Minister's Laptop Scheme Students' Merit List for the Award of Laptops - Mehran University of Engineering Technology, Jamshoro
Prime Minister's Laptop Scheme Students' Merit List for the Award of Laptops - Mehran University of Engineering Technology, Jamshoro Campus Department/ School Degree Level Merit Selection Year of Study Name of Student Father's Name CNIC Percentage CGPA CEAD, MUET, Jamshoro Architecture Bachelors Selected 1st Abdul Hai Gul Muneer 4130260760693 81.4 3.30 Amina Ayoub MUHAMMAD AYOUB 4130396570396 83.72 3.39 Faisal MUHAMMAD NAWAZ 4420498098565 81.25 3.30 Faiza Mehmood Shah Syed Mehmood Hussain 8210399174214 72.81 2.98 Hina Kamal Mustafa Kamal 82818 87.27 3.52 Imran Hussain Muhammad Jameel 4130412629439 72.36 2.97 Khudija Bano Fatima Muhammad Ali Munim 3720181788808 82.59 3.35 Malik Muhammad Maaz Malik Muhammad Younis 4130341726445 73.45 3.01 MUHAMMAD BILAL KHAN Muhammad Yousif Khan 4130329392143 82.04 3.33 Muhammad Khalid Khan Muhammad Akram Khan 1330221161845 70.3 2.89 Muhib Anwar 41303862275615 88.18 3.55 Mukhlis ALI MUHAMMAD 4130621578210 81.7 3.31 Nayab Imama Ghousi Abdul Ghafar Ghousi 4130368656664 80 3.25 Nimra Muhammad Ramzan 4410493138192 81.00 3.29 Saher Abid Abbas 4130384716342 75.00 3.07 Samreen Syed Qurban Ali Shah 4140983729066 74.36 3.04 Shahdad Khan Mari Kabho Khan Mari 4130724120671 85.18 3.44 Shumaila Parveen Shah Muhammad 3120271927940 73.63 3.01 Tania Panhwar Lal Muhammad 4250168068518 75.00 3.07 Touseef Ahmed Rasheed Ahmed 4410182364487 86.18 3.48 WAHAB ALI ABDUL RAZZAQUE 4130684900141 81.09 3.29 81.1 3.29 Zarfishan Ehsan Ali Rizvi 4130251762874 80 3.25 Zubail Ahmed MAQBOOL AHMED 4130346779829 86.36 3.49 3.49 2nd Faisal -
Regime Type and Women's Substantive Representation in Pakistan: a Study in Socio Political Constraints on Policymaking
REGIME TYPE AND WOMEN’S SUBSTANTIVE REPRESENTATION IN PAKISTAN: A STUDY IN SOCIO POLITICAL CONSTRAINTS ON POLICYMAKING PhD DISSERTATION Submitted by Naila Maqsood Reg. No. NDU-GPP/Ph.D-009/F-002 Supervisor Dr. Sarfraz Hussain Ansari Department of Government & Public Policy Faculty of Contemporary Studies National Defence University Islamabad 2016 REGIME TYPE AND WOMEN’S SUBSTANTIVE REPRESENTATION IN PAKISTAN: A STUDY IN SOCIO POLITICAL CONSTRAINTS ON POLICY MAKING PhD DISSERTATION Submitted by Naila Maqsood Reg. No. NDU-GPP/Ph.D-009/F-002 This Dissertation is submitted to National Defence University, Islamabad in partial fulfillment for the degree of Doctor of Philosophy in Government and Public Policy Supervisor Dr. Sarfraz Hussain Ansari Department of Government & Public Policy Faculty of Contemporary Studies National Defence University Islamabad 2016 Certificate of Completion It is hereby recommended that the dissertation submitted by Ms. Naila Maqsood titled “Regime Type and Women’s Substantive Representation in Pakistan: A Study in Socio-Political Constraints on Policymaking” has been accepted in the partial fulfillment of the requirements for the degree of PhD in the discipline of Government & Public Policy. __________________________________ Supervisor __________________________________ External Examiner Countersigned By: …………………………………………… …………………………………….. Controller Examination Head of department Supervisor’s Declaration This is to certify that PhD dissertation submitted by Ms. Naila Maqsood titled “Regime Type and Women’s Substantive Representation in Pakistan: A Study in Socio-Political Constraints on Policymaking” is supervised by me, and is submitted to meet the requirements of PhD degree. Date: _____________ Dr. Sarfraz Hussain Ansari Supervisor Scholar’s Declaration I hereby declare that the thesis submitted by me titled “Regime Type and Women’s Substantive Representation in Pakistan: A Study in Socio- Political Constraints on Policymaking” is based on my own research work and has not been submitted to any other institution for any other degree. -

Merit Call List III 2020
Mehran University of Engineering and Technology, Jamshoro DIRECTORATE OF ADMISSIONS Third Provisional Interview Call List For Session 2020-21 (20 Batch) The Candidates are required to bring all original Documents alongwith one set of attested photostat copies as per their interview schedule from 28/12/2020 to 29/12/2020. A little larger number of candidates have been called for interview to avoid delay in admissions The interviews include B.E, B.ARCH, B.CRP and B.S Programs. Any Mistake if Detected Lateron shall be Rectified Accordingly Interview Date: 28-12-2020 Districts:Badin, Dadu, Hyderabad, Jamshoro, Karachi, Matiari, MirpurKhas, Tando Allahyar, Umerkot Interview Date: 29-12-2020 Districts:Ghotki, Kambar, Kashmore, Khairpur, Larkana, N. Feroze, S. B. Abad, Sanghar, Shikarpur, Sukkur Detailed Interview Schedule will be followed shortly Sr. Seat Net Test Name Father's Name Surname District U/R SSC HSC Group MUE Hafiz CPN No. No. HSC Score 1 12255 Waqas Ali Muhammad Tayab Arain Badin U 576 668 668 43 P.E N.A No 50.795 2 20246 Abdul Manan Abdul Latif Khatri Khatri Badin U 566 702 680 41 P.M N.A No 49.804 1 20268 Divya Sharma Gotam Kumar Birhaman Badin R 683 791 791 56 P.M N.A No 63.208 2 20370 Kiran Nisar Ahmed Memon Badin R 624 749 738 56 P.M N.A No 61.068 3 20272 Sansar Abdul Sattar Memon Badin R 570 692 692 53 P.M N.A No 57.379 4 20243 Farhan Muhammad Ali Zour Badin R 616 763 752 46 P.M N.A No 55.356 5 20379 Shafique Ahmed Abdul Aziz Soomro Badin R 473 696 696 50 P.M N.A No 54.237 6 20508 Sangeeta Lakhoo Mal Khokhar Badin R 606 672