Euler Tour Technique 1 the Dynamic Connectivity Problem with Forests 2
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
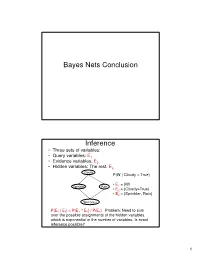
Bayes Nets Conclusion Inference
Bayes Nets Conclusion Inference • Three sets of variables: • Query variables: E1 • Evidence variables: E2 • Hidden variables: The rest, E3 Cloudy P(W | Cloudy = True) • E = {W} Sprinkler Rain 1 • E2 = {Cloudy=True} • E3 = {Sprinkler, Rain} Wet Grass P(E 1 | E 2) = P(E 1 ^ E 2) / P(E 2) Problem: Need to sum over the possible assignments of the hidden variables, which is exponential in the number of variables. Is exact inference possible? 1 A Simple Case A B C D • Suppose that we want to compute P(D = d) from this network. A Simple Case A B C D • Compute P(D = d) by summing the joint probability over all possible values of the remaining variables A, B, and C: P(D === d) === ∑∑∑ P(A === a, B === b,C === c, D === d) a,b,c 2 A Simple Case A B C D • Decompose the joint by using the fact that it is the product of terms of the form: P(X | Parents(X)) P(D === d) === ∑∑∑ P(D === d | C === c)P(C === c | B === b)P(B === b | A === a)P(A === a) a,b,c A Simple Case A B C D • We can avoid computing the sum for all possible triplets ( A,B,C) by distributing the sums inside the product P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a 3 A Simple Case A B C D This term depends only on B and can be written as a 2- valued function fA(b) P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a A Simple Case A B C D This term depends only on c and can be written as a 2- valued function fB(c) === === === === === === P(D d) ∑∑∑ P(D d | C c)∑∑∑P(C c | B b)f A(b) c b …. -

Tree Structures
Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A. -

A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width
Introduction Preliminary Definitions Pathwidth Algorithm Summary A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width Kevin Cattell Michael J. Dinneen Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. Canada V8W 3P6 Information Processing Letters 57 (1996) 197–203 Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Pathwidth Algorithm Summary Outline 1 Introduction Motivation History 2 Preliminary Definitions Boundaried graphs Path-decompositions Topological tree obstructions 3 Pathwidth Algorithm Main result Linear-time algorithm Proof of correctness Other results Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary Motivation Pathwidth is related to several VLSI layout problems: vertex separation link gate matrix layout edge search number ... Usefullness of bounded treewidth in: study of graph minors (Robertson and Seymour) input restrictions for many NP-complete problems (fixed-parameter complexity) Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary History General problem(s) is NP-complete Input: Graph G, integer t Question: Is tree/path-width(G) ≤ t? Algorithmic development (fixed t): O(n2) nonconstructive treewidth algorithm by Robertson and Seymour (1986) O(nt+2) treewidth algorithm due to Arnberg, Corneil and Proskurowski (1987) O(n log n) treewidth algorithm due to Reed (1992) 2 O(2t n) treewidth algorithm due to Bodlaender (1993) O(n log2 n) pathwidth algorithm due to Ellis, Sudborough and Turner (1994) Kevin Cattell, Michael J. Dinneen, Michael R. -

Lowest Common Ancestors in Trees and Directed Acyclic Graphs1
Lowest Common Ancestors in Trees and Directed Acyclic Graphs1 Michael A. Bender2 3 Martín Farach-Colton4 Giridhar Pemmasani2 Steven Skiena2 5 Pavel Sumazin6 Version: We study the problem of finding lowest common ancestors (LCA) in trees and directed acyclic graphs (DAGs). Specifically, we extend the LCA problem to DAGs and study the LCA variants that arise in this general setting. We begin with a clear exposition of Berkman and Vishkin’s simple optimal algorithm for LCA in trees. The ideas presented are not novel theoretical contributions, but they lay the foundation for our work on LCA problems in DAGs. We present an algorithm that finds all-pairs-representative : LCA in DAGs in O~(n2 688 ) operations, provide a transitive-closure lower bound for the all-pairs-representative-LCA problem, and develop an LCA-existence algorithm that preprocesses the DAG in transitive-closure time. We also present a suboptimal but practical O(n3) algorithm for all-pairs-representative LCA in DAGs that uses ideas from the optimal algorithms in trees and DAGs. Our results reveal a close relationship between the LCA, all-pairs-shortest-path, and transitive-closure problems. We conclude the paper with a short experimental study of LCA algorithms in trees and DAGs. Our experiments and source code demonstrate the elegance of the preprocessing-query algorithms for LCA in trees. We show that for most trees the suboptimal Θ(n log n)-preprocessing Θ(1)-query algorithm should be preferred, and demonstrate that our proposed O(n3) algorithm for all- pairs-representative LCA in DAGs performs well in both low and high density DAGs. -

Trees a Tree Is a Graph Which Is (A) Connected and (B) Has No Cycles (Acyclic)
Trees A tree is a graph which is (a) Connected and (b) has no cycles (acyclic). 1 Lemma 1 Let the components of G be C1; C2; : : : ; Cr, Suppose e = (u; v) 2= E, u 2 Ci; v 2 Cj. (a) i = j ) !(G + e) = !(G). (b) i 6= j ) !(G + e) = !(G) − 1. (a) v u (b) u v 2 Proof Every path P in G + e which is not in G must contain e. Also, !(G + e) ≤ !(G): Suppose (x = u0; u1; : : : ; uk = u; uk+1 = v; : : : ; u` = y) is a path in G + e that uses e. Then clearly x 2 Ci and y 2 Cj. (a) follows as now no new relations x ∼ y are added. (b) Only possible new relations x ∼ y are for x 2 Ci and y 2 Cj. But u ∼ v in G + e and so Ci [ Cj becomes (only) new component. 2 3 Lemma 2 G = (V; E) is acyclic (forest) with (tree) components C1; C2; : : : ; Ck. jV j = n. e = (u; v) 2= E, u 2 Ci; v 2 Cj. (a) i = j ) G + e contains a cycle. (b) i 6= j ) G + e is acyclic and has one less com- ponent. (c) G has n − k edges. 4 (a) u; v 2 Ci implies there exists a path (u = u0; u1; : : : ; u` = v) in G. So G + e contains the cycle u0; u1; : : : ; u`; u0. u v 5 (a) v u Suppose G + e contains the cycle C. e 2 C else C is a cycle of G. C = (u = u0; u1; : : : ; u` = v; u0): But then G contains the path (u0; u1; : : : ; u`) from u to v – contradiction. -
![Arxiv:1901.04560V1 [Math.CO] 14 Jan 2019 the flexibility That Makes Hypergraphs Such a Versatile Tool Complicates Their Analysis](https://docslib.b-cdn.net/cover/7775/arxiv-1901-04560v1-math-co-14-jan-2019-the-exibility-that-makes-hypergraphs-such-a-versatile-tool-complicates-their-analysis-817775.webp)
Arxiv:1901.04560V1 [Math.CO] 14 Jan 2019 the flexibility That Makes Hypergraphs Such a Versatile Tool Complicates Their Analysis
MINIMALLY CONNECTED HYPERGRAPHS MARK BUDDEN, JOSH HILLER, AND ANDREW PENLAND Abstract. Graphs and hypergraphs are foundational structures in discrete mathematics. They have many practical applications, including the rapidly developing field of bioinformatics, and more generally, biomathematics. They are also a source of interesting algorithmic problems. In this paper, we define a construction process for minimally connected r-uniform hypergraphs, which captures the intuitive notion of building a hypergraph piece-by-piece, and a numerical invariant called the tightness, which is independent of the construc- tion process used. Using these tools, we prove some fundamental properties of minimally connected hypergraphs. We also give bounds on their chromatic numbers and provide some results involving edge colorings. We show that ev- ery connected r-uniform hypergraph contains a minimally connected spanning subhypergraph and provide a polynomial-time algorithm for identifying such a subhypergraph. 1. Introduction Graphs and hypergraphs provide many beautiful results in discrete mathemat- ics. They are also extremely useful in applications. Over the last six decades, graphs and their generalizations have been used for modeling many biological phenomena, ranging in scale from protein-protein interactions, individualized cancer treatments, carcinogenesis, and even complex interspecial relationships [12, 15, 16, 19, 22]. In the last few years in particular, hypergraphs have found an increasingly prominent position in the biomathematical literature, as they allow scientists and practitioners to model complex interactions between arbitrarily many actors [22]. arXiv:1901.04560v1 [math.CO] 14 Jan 2019 The flexibility that makes hypergraphs such a versatile tool complicates their analysis. Because of this, many different algorithms and metrics have been devel- oped to assist with their application [18, 23]. -

Section 11.1 Introduction to Trees Definition
Section 11.1 Introduction to Trees Definition: A tree is a connected undirected graph with no simple circuits. : A circuit is a path of length >=1 that begins and ends a the same vertex. d d Tournament Trees A common form of tree used in everyday life is the tournament tree, used to describe the outcome of a series of games, such as a tennis tournament. Alice Antonia Alice Anita Alice Abigail Abigail Alice Amy Agnes Agnes Angela Angela Angela Audrey A Family Tree Much of the tree terminology derives from family trees. Gaea Ocean Cronus Phoebe Zeus Poseidon Demeter Pluto Leto Iapetus Persephone Apollo Atlas Prometheus Ancestor Tree An inverted family tree. Important point - it is a binary tree. Iphigenia Clytemnestra Agamemnon Leda Tyndareus Aerope Atreus Catreus Forest Graphs containing no simple circuits that are not connected, but each connected component is a tree. Theorem An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices. Rooted Trees Once a vertex of a tree has been designated as the root of the tree, it is possible to assign direction to each of the edges. Rooted Trees g a e f e c b b d a d c g f root node a internal vertex parent of g b c d e f g leaf siblings h i a b c d e f g h i h i ancestors of and a b c d e f g subtree with b as its h i root subtree with c as its root m-ary trees A rooted tree is called an m-ary tree if every internal vertex has no more than m children. -

An Algorithm for the Exact Treedepth Problem James Trimble School of Computing Science, University of Glasgow Glasgow, Scotland, UK [email protected]
An Algorithm for the Exact Treedepth Problem James Trimble School of Computing Science, University of Glasgow Glasgow, Scotland, UK [email protected] Abstract We present a novel algorithm for the minimum-depth elimination tree problem, which is equivalent to the optimal treedepth decomposition problem. Our algorithm makes use of two cheaply-computed lower bound functions to prune the search tree, along with symmetry-breaking and domination rules. We present an empirical study showing that the algorithm outperforms the current state-of-the-art solver (which is based on a SAT encoding) by orders of magnitude on a range of graph classes. 2012 ACM Subject Classification Theory of computation → Graph algorithms analysis; Theory of computation → Algorithm design techniques Keywords and phrases Treedepth, Elimination Tree, Graph Algorithms Supplement Material Source code: https://github.com/jamestrimble/treedepth-solver Funding James Trimble: This work was supported by the Engineering and Physical Sciences Research Council (grant number EP/R513222/1). Acknowledgements Thanks to Ciaran McCreesh, David Manlove, Patrick Prosser and the anonymous referees for their helpful feedback, and to Robert Ganian, Neha Lodha, and Vaidyanathan Peruvemba Ramaswamy for providing software for the SAT encoding. 1 Introduction This paper presents a practical algorithm for finding an optimal treedepth decomposition of a graph. A treedepth decomposition of graph G = (V, E) is a rooted forest F with node set V , such that for each edge {u, v} ∈ E, we have either that u is an ancestor of v or v is an ancestor of u in F . The treedepth of G is the minimum depth of a treedepth decomposition of G, where depth is defined as the maximum number of vertices along a path from the root of the tree to a leaf. -

Merkle Trees and Directed Acyclic Graphs (DAG) As We've Discussed, the Decentralized Web Depends on Linked Data Structures
Merkle trees and Directed Acyclic Graphs (DAG) As we've discussed, the decentralized web depends on linked data structures. Let's explore what those look like. Merkle trees A Merkle tree (or simple "hash tree") is a data structure in which every node is hashed. +--------+ | | +---------+ root +---------+ | | | | | +----+---+ | | | | +----v-----+ +-----v----+ +-----v----+ | | | | | | | node A | | node B | | node C | | | | | | | +----------+ +-----+----+ +-----+----+ | | +-----v----+ +-----v----+ | | | | | node D | | node E +-------+ | | | | | +----------+ +-----+----+ | | | +-----v----+ +----v-----+ | | | | | node F | | node G | | | | | +----------+ +----------+ In a Merkle tree, nodes point to other nodes by their content addresses (hashes). (Remember, when we run data through a cryptographic hash, we get back a "hash" or "content address" that we can think of as a link, so a Merkle tree is a collection of linked nodes.) As previously discussed, all content addresses are unique to the data they represent. In the graph above, node E contains a reference to the hash for node F and node G. This means that the content address (hash) of node E is unique to a node containing those addresses. Getting lost? Let's imagine this as a set of directories, or file folders. If we run directory E through our hashing algorithm while it contains subdirectories F and G, the content-derived hash we get back will include references to those two directories. If we remove directory G, it's like Grace removing that whisker from her kitten photo. Directory E doesn't have the same contents anymore, so it gets a new hash. As the tree above is built, the final content address (hash) of the root node is unique to a tree that contains every node all the way down this tree. -

Problem Set 2 Out: April 15 Due: April 22
CS 38 Introduction to Algorithms Spring 2014 Problem Set 2 Out: April 15 Due: April 22 Reminder: you are encouraged to work in groups of two or three; however you must turn in your own write-up and note with whom you worked. You may consult the course notes and the optional text (CLRS). The full honor code guidelines can be found in the course syllabus. Please attempt all problems. To facilitate grading, please turn in each problem on a separate sheet of paper and put your name on each sheet. Do not staple the separate sheets. 1. Recall that a prefix-free encoding scheme can be represented by a binary tree, and that the Huffman code algorithm gives an efficient way to construct an optimal such tree from the probabilities p1; p2; : : : ; pn of n symbols. In this problem, you will show that the average length of such an encoding scheme is at most one larger than the entropy (which is the information- theoretic best-possible). The entropy of the distribution given by p = (p1; p2; : : : ; pn) is defined to be Xn H(p) = − log(pi) · pi: i=1 (a) Prove that for any list of positive integers `1; `2; : : : ; `n satisfying Xn − 2 `i ≤ 1; i=1 there is a binary tree with distinct root-leaf paths having lengths `1; `2; : : : ; `n. Hint: start from the full binary tree and delete subtrees. (b) Let p = (p1; : : : ; pn) give the probabilities of n symbols. Prove that if `1; : : : ; `n are the encoding lengths in an optimal prefix-free encoding scheme for this distribution, then the average encoding length, Xn `ipi; i=1 is at most H(p) + 1. -

Introduction to Trees
Trees CMSC 420: Lecture 5 Hierarchies Many ways to represent tree-like information: A I. A 1. B C B a. D i. E D F G b. F 2. C E a. G linked hierarchy A outlines, E D indentations B G C F (((E):D), F):B, (G):C):A nested, labeled parenthesis nested sets Definition – Rooted Tree • Λ is a tree • If T1, T2, ..., Tk are trees with roots r1, r2, ..., rk and r is a node ∉ any Ti, then the structure that consists of the Ti, node r, and edges (r, ri) is also a tree. r r1 r3 r2 r4 r1 r2 r3 r4 T1 T3 T4 T2 Terminology • r is the parent of its children r1, r2, ..., rk. • r1, r2, ..., rk are siblings. • root = distinguished node, usually drawn root at top. Has no parent. path from internal root to w • If all children of a node are Λ, the node is node u a leaf. Otherwise, the node is a internal node. parent of w • A path in the tree is a sequence of nodes u1, u2, ..., um such that each of the edges children of u (u, u ) exists. w i+1 (they are siblings) leaves • A node u is an ancestor of v if there is a path from u to v. • A node u is a descendant of v if there is a path from v to u. Height & Depth • The height of node u is the length of the longest path from u to a leaf. • The depth of node u is the length of the path from the root to u. -

UNIT 6C Organizing Data: Trees and Graphs Last Lecture
UNIT 6C Organizing Data: Trees and Graphs 15110 Principles of Computing, 1 Carnegie Mellon University Last Lecture • Hash tables – Using hash function to map keys of different data types to array indices – Constant search time if the load factor is small • Associative arrays in Ruby 15110 Principles of Computing, 2 Carnegie Mellon University 1 This Lecture • Non‐linear data structures – Trees, specifically, binary trees – Graphs 15110 Principles of Computing, 3 Carnegie Mellon University Trees 15110 Principles of Computing, 4 Carnegie Mellon University 2 Trees • A tree is a hierarchical data structure. – Every tree has a node called the root. – Each node can have 1 or more nodes as children. – A node that has no children is called a leaf. • A common tree in computing is a binary tree. – A binary tree consists of nodes that have at most 2 children. – A complete binary tree has the maximum number of nodes on each of its levels. • Applications: data compression, file storage, game trees 15110 Principles of Computing, 5 Carnegie Mellon University Binary Tree 84 41 96 24 50 98 13 37 Which one is the root? Which ones are the leaves? Is this a complete binary tree? What is the height of this tree? 15110 Principles of Computing, 6 Carnegie Mellon University 3 Binary Tree 84 41 96 24 50 98 13 37 The root has the data value 84. There are 4 leaves in this binary tree: 13, 37, 50, 98. This binary tree is not complete. This binary tree has height 3. 15110 Principles of Computing, 7 Carnegie Mellon University Binary Trees: Implementation • One common implementation of binary trees uses nodes like a linked list does.