Simulation and Modeling Techniques for Signal Integrity and Electromagnetic Interference on High Frequency Electronic Systems
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Modeling System Signal Integrity Uncertainty Considerations
WHITE PAPER Intel® FPGA Modeling System Signal Integrity Uncertainty Considerations Authors Abstract Ravindra Gali This white paper describes signal integrity (SI) mechanisms that cause system-level High-Speed I/O Applications timing uncertainty and how these mechanisms are modeled in the Intel® Quartus® Engineering, Intel® Corporation Prime software Timing Analyzer to achieve timing closure for external memory interface designs. Zhi Wong By using the Intel Quartus Prime software to achieve timing closure for external High-Speed I/O Applications memory interfaces, a designer does not need to allocate a separate SI timing Engineering, Intel Corporation budget to account for simultaneous switching output (SSO), simultaneous Navid Azizi switching input (SSI), intersymbol interference (ISI), and board-level crosstalk for Software Engineeringr flip-chip device families such as Stratix® IV and Arria® II FPGAs for typical user Intel Corporation implementation of external memory interfaces following good board design practices. John Oh High-Speed I/O Applications Introduction Engineering, Intel Corporation The widening performance gap between FPGAs, microprocessors, and memory Arun VR devices, along with the growth of memory-intensive applications, are driving the Memory I/O Applications Engineering, need for faster memory technologies. This push to higher bandwidths has been Intel Corporation accompanied by an increase in the signal count and the signaling rates of FPGAs and memory devices. In order to attain faster bandwidths, device makers continue to reduce the supply voltage. Initially, industry-standard DIMMs operated at 5 V. However, due to improvements in DRAM storage density, the operating voltage was decreased to 3.3 V (SDR), then to 2.5V (DDR), 1.8 V (DDR2), 1.5 V (DDR3), and 1.35 V (DDR3) to allow the memory to run faster and consume less power. -
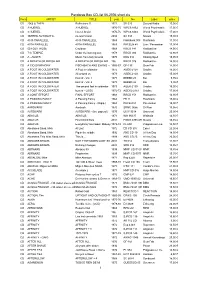
Pandoras Box CD-List 06-2006 Short
Pandoras Box CD-list 06-2006 short.xls Form ARTIST TITLE year No Label price CD 2066 & THEN Reflections !! 1971 SB 025 Second Battle 15,00 € CD 3 HUEREL 3 HUEREL 1970-75 WPC6 8462 World Psychedelic 17,00 € CD 3 HUEREL Huerel Arisivi 1970-75 WPC6 8463 World Psychedelic 17,00 € CD 3SPEED AUTOMATIC no man's land 2004 SA 333 Nasoni 15,00 € CD 49 th PARALLELL 49 th PARALLELL 1969 Flashback 008 Flashback 11,90 € CD 49TH PARALLEL 49TH PARALLEL 1969 PACELN 48 Lion / Pacemaker 17,90 € CD 50 FOOT HOSE Cauldron 1968 RRCD 141 Radioactive 14,90 € CD 7 th TEMPLE Under the burning sun 1978 RRCD 084 Radioactive 14,90 € CD A - AUSTR Music from holy Ground 1970 KSG 014 Kissing Spell 19,95 € CD A BREATH OF FRESH AIR A BREATH OF FRESH AIR 196 RRCD 076 Radioactive 14,90 € CD A CID SYMPHONY FISCHBACH AND EWING - (21966CD) -67 GF-135 Gear Fab 14,90 € CD A FOOT IN COLDWATER A Foot in coldwater 1972 AGEK-2158 Unidisc 15,00 € CD A FOOT IN COLDWATER All around us 1973 AGEK-2160 Unidisc 15,00 € CD A FOOT IN COLDWATER best of - Vol. 1 1973 BEBBD 25 Bei 9,95 € CD A FOOT IN COLDWATER best of - Vol. 2 1973 BEBBD 26 Bei 9,95 € CD A FOOT IN COLDWATER The second foot in coldwater 1973 AGEK-2159 Unidisc 15,00 € CD A FOOT IN COLDWATER best of - (2CD) 1972-73 AGEK2-2161 Unidisc 17,90 € CD A JOINT EFFORT FINAL EFFORT 1968 RRCD 153 Radioactive 14,90 € CD A PASSING FANCY A Passing Fancy 1968 FB 11 Flashback 15,00 € CD A PASSING FANCY A Passing Fancy - (Digip.) 1968 PACE-034 Pacemaker 15,90 € CD AARDVARK Aardvark 1970 SRMC 0056 Si-Wan 19,95 € CD AARDVARK AARDVARK - (lim. -

The Printed Circuit Designer's Guide To... Signal Integrity by Example
PEER REVIEWERS This book has been reviewed for technical accuracy by the following experts from the PCB industry. Happy Holden Consulting Technical Editor, I-Connect007 Happy Holden is the retired director of electronics and innovations for Gentex Corporation. Happy is the former chief technical officer for the world’s largest PCB fabricator, Hon Hai Precision Industries (Foxconn). Prior to Foxconn, Holden was the senior PCB technologist for Mentor Graphics and advanced technology manager at Nan Ya/ Westwood Associates and Merix. Happy previously worked at Hewlett-Packard for over 28 years as director of PCB R&D and manufacturing engineering manager. He has been involved in advanced PCB technologies for over 47 years. Eric Bogatin Eric Bogatin is currently the dean of the Teledyne LeCroy Signal Integrity Academy. Additionally, he is an adjunct professor at the University of Colorado- Boulder in the ECEE department, where he teaches a graduate class in signal integrity and is also the editor of Signal Integrity Journal. Bogatin received his BS in physics from MIT, and MS and PhD in physics from the University of Arizona in Tucson. Eric has held senior engineering and management positions at Bell Labs, Raychem, Sun Microsystems, Ansoft and Interconnect Devices. Bogatin has written six technical books in the field, and presented classes and lectures on signal integrity worldwide. MEET THE AUTHOR Fadi Deek Signal/Power Integrity Specialist Corporate Application Engineer In 2005, Fadi received his B.S. degree in computer and communications from the American University of Science and Technology (AUST) in Beirut, Lebanon. That same year, he joined Fidus Systems as a design engineer. -

Leonard Bernstein
chamber music with a modernist edge. His Piano Sonata (1938) reflected his Leonard Bernstein ties to Copland, with links also to the music of Hindemith and Stravinsky, and his Sonata for Clarinet and Piano (1942) was similarly grounded in a neoclassical aesthetic. The composer Paul Bowles praised the clarinet sonata as having a "tender, sharp, singing quality," as being "alive, tough, integrated." It was a prescient assessment, which ultimately applied to Bernstein’s music in all genres. Bernstein’s professional breakthrough came with exceptional force and visibility, establishing him as a stunning new talent. In 1943, at age twenty-five, he made his debut with the New York Philharmonic, replacing Bruno Walter at the last minute and inspiring a front-page story in the New York Times. In rapid succession, Bernstein Leonard Bernstein photo © Susech Batah, Berlin (DG) produced a major series of compositions, some drawing on his own Jewish heritage, as in his Symphony No. 1, "Jeremiah," which had its first Leonard Bernstein—celebrated as one of the most influential musicians of the performance with the composer conducting the Pittsburgh Symphony in 20th century—ushered in an era of major cultural and technological transition. January 1944. "Lamentation," its final movement, features a mezzo-soprano He led the way in advocating an open attitude about what constituted "good" delivering Hebrew texts from the Book of Lamentations. In April of that year, music, actively bridging the gap between classical music, Broadway musicals, Bernstein’s Fancy Free was unveiled by Ballet Theatre, with choreography by jazz, and rock, and he seized new media for its potential to reach diverse the young Jerome Robbins. -

The Routledge Companion to Actor-Network Theory
The Routledge Companion to Actor-Network Theory This companion explores ANT as an intellectual practice, tracking its movements and engagements with a wide range of other academic and activist projects. Showcasing the work of a diverse set of ‘second generation’ ANT scholars from around the world, it highlights the exciting depth and breadth of contemporary ANT and its future possibilities. The companion has 38 chapters, each answering a key question about ANT and its capacities. Early chapters explore ANT as an intellectual practice and highlight ANT’s dialogues with other fields and key theorists. Others open critical, provocative discussions of its limitations. Later sections explore how ANT has been developed in a range of so cial scientific fields and how it has been used to explore a wide range of scales and sites. Chapters in the final section discuss ANT’s involvement in ‘real world’ endeavours such as disability and environmental activism, and even running a Chilean hospital. Each chapter contains an overview of relevant work and introduces original examples and ideas from the authors’ recent research. The chapters orient readers in rich, complex fields and can be read in any order or combination. Throughout the volume, authors mobilise ANT to explore and account for a range of exciting case studies: from wheelchair activism to parliamentary decision-making; from racial profiling to energy consumption monitoring; from queer sex to Korean cities. A comprehensive introduction by the editors explores the significance of ANT more broadly and provides an overview of the volume. The Routledge Companion to Actor-Network Theory will be an inspiring and lively companion to aca- demics and advanced undergraduates and postgraduates from across many disciplines across the social sciences, including Sociology, Geography, Politics and Urban Studies, Environmental Studies and STS, and anyone wishing to engage with ANT, to understand what it has already been used to do and to imagine what it might do in the future. -

High Speed Signal Integrity Analysis and Differential Signaling
High Speed Signal Integrity Analysis and Differential Signaling Project Report of EE201C: Modeling of VLSI Circuits and Systems Tongtong Yu, UID: 904025158 Zhiyuan Shen, UID: 803987916 Abstract— This course project is designated for independent electric mechanism of semiconductor circuit doesn’t change study of various topics relating to VLSI modeling. In our very much, so the concentration is on the interconnects and project, the first part is an extension of the class presentation packaging. where we introduced the basic idea of signal integrity. Here we address the philosophy behind frequency domain and time The impact of to the system can be classified to signal domain. Then, we give two examples of interconnects, a critical integrity, which refers to the contamination of signal’s in- issue related to signal integrity. The second part is about tegrity due to parasitic effects of interconnects and packaging, differential signaling used in high speed application. After compared with ideal case. This may result in unsatisfactory analyzing general principles, we simulate two parallel-trace performance. For example, we design the systems for 10Gbps; transmission line, which has practical meaning in real design case. Maybe this project is not fancy, but we believe all the however, due to this effect, it can only achieve 5Gbps. Also, fundamentals provided here and those reference list in the end this may produce inaccurate logic state and even logical are the best material for everyone who wants to go further in failure. This impact can be classified in two ways this area. 1) Delay, distortion and cross-talk directly happening on We would like to express our deepest gratitude to Prof. -

Signal Integrity Analysis and Simulation Tools Include IBIS Models
High Frequency Products From September 2004 High Frequency Electronics Copyright ® 2004 Summit Technical Media, LLC HIGH-SPEED MODELS Signal Integrity Analysis and Simulation Tools Include IBIS Models By John Olah and Sanjeev Gupta, Agilent EEsof EDA, and Carlos Chavez-Dagostino, Altera Corporation ignal integrity is a several hybrid-domain simulation techniques, This issue’s cover highlights major concern for where the simulator is conversant in both the introduction of Agilent Sengineers working time and frequency domain and can combine Technologies’ ADS2004A, on high data rate designs. models suitable for either domain. This article which now includes Effects such as crosstalk, describes the types of models that need to be greatly enhanced capa- coupling and delays in taken together for high-speed signal integrity bilities for signal integrity transmission lines have a analysis, and illustrates their use in a simula- modeling in both time big impact on signal tion of a high-speed memory circuit. and frequency domains integrity. High-speed dig- ital board designers can Requirements for High-Speed now use design tools that combine time- Signal Integrity Simulations domain IC-specific I/O Buffer Information In broad terms, there are three important Specification (IBIS) models with accurate simulation requirements for analog high- transmission line models to get a better speed signal integrity characterization: understanding of the signal distortion due to coupling and delays. 1. A hybrid-domain simulator that handles time-domain and frequency-domain models Introduction 2. Accurate transmission line structures (best In terms of analog simulators, historically, described in the frequency-domain) there have been two main camps; time- 3. -

10 Ways ADS Overcomes Signal and Power Integrity Challenges
Keysight Technologies 10 Ways ADS Overcomes Signal and Power Integrity Challenges Technical Overview 02 | Keysight | 8 Ways ADS Overcomes Signal and Power Integrity Challenges - Technical Overview Keysight EEsof EDA’s Advanced Design System (ADS) software is the world’s leading electronic design automation solution for RF, microwave, and high-speed digital applications. ADS features a host of new, technologies designed to improve productivity, including two electromagnetic (EM) software solutions specifically created to help signal and power integrity engineers improve high-speed link performance in PCB designs. What follows is a listing of 8 ways in which ASD can help you, the engineer, overcome your signal and power integrity challenges. 1. ADS provides speed and accuracy for your SI EM characterization ........................Page 2 2. ADS simplifies the use of S-parameter files for your parts .......................................Page 4 3. ADS provides access to industry-leading channel simulator technology ...................................................................................................Page 6 4. ADS stays ahead of technology waves (such as PAM-4) ..........................................Page 9 5. ADS accelerates DDR4 simulation methodologies ....................................................Page 12 6. ADS puts power in the hands of designers (PI analyses) ..........................................Page 15 7. ADS enables flat PDN impedance responses ............................................................Page -

The Alignment of Screens
The Alignment of Screens Felipe Raglianti , B.A.; M.A. Submitted for the degree of Doctor of Philosophy (PhD) Department of Sociology, Lancaster University, 2016 Declaration I declare that this thesis is my own work and that it has not been submitted in any form for the award of a higher degree elsewhere. Felipe Raglianti, June 2016 1 Abstract This thesis makes a distinction between screen and surface. It proposes that an inquiry into screens includes, but is not limited to, the study of surfaces. Screens and screening practices are about doing both divisions and vision. The habit of reducing screens to the display neglects their capacity to emplace separations (think of folding screens). In this thesis an investigation of screens becomes a matter of asking how surfaces and the gaps in between them articulate alignments of people and things with displays that, in practice, always leave something out of sight. Rather than losing touch with screens by reducing them to surfaces, in other words, I am interested in alternative screen configurations. For this task I sketch an approach that touches on screens through the figures of lines, surfaces, textures, folds, knots and cuts. Lines help me to make the case for thinking about screens as alignments. I then ask what kinds of observers emerge from reducing screens to single or digital surfaces. I trace that concern with Google Glass, a pair of “smartglasses” with a transparent display. To distinguish between screen and surface I suggest, through a study of biodetection and assistance dogs, how to qualify or texture screens within webs of relations. -

Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation
Paper SAS4281-2020 Introducing PROC SIMSYSTEM for Systematic Nonnormal Simulation Bucky Ransdell and Randy Tobias, SAS Institute Inc. ABSTRACT Simulation is a key element in how decisions are made in a wide variety of fields, from finance and insurance to engineering and statistics. Analysts use simulation to estimate the probability that a business process will succeed, that an insurance portfolio will fail, or that a statistical method will control Type I error. Often, the base case that is used to devise such processes depends on assuming that random variation is normal (Gaussian). Normal variation is common and is often easier to compute with. But it is still an assumption, so robust simulation studies should explore what happens when that assumption is violated. The SIMSYSTEM procedure, new in SAS® Visual Statistics 8.5, enables you to simulate random variation from a wide class of distributions. You can use PROC SIMSYSTEM to generate random variates with any possible values for skewness and kurtosis, which define the asymmetry and tail behavior of the underlying distribution. Key tools are computational facilities for handling the Pearson and Johnson families of distributions, whose parameters span this skewness/kurtosis space. This paper introduces PROC SIMSYSTEM and demonstrates its utility with examples that simulate complex processes in science and industry. INTRODUCTION—MOMENTS OF DISTRIBUTIONS Simulation is widely used in science, engineering, and business to study the behavior of complex systems. It is an essential tool for studying a real-world system for which conducting controlled experiments is not feasible; examples include the earth’s climate, the global economy, or even (as in the extended example later in this paper) personal finance. -

Cangoma Calling Spirits and Rhythms of Freedom in Brazilian Jongo Slavery Songs
Cangoma Calling Spirits and Rhythms of Freedom in Brazilian Jongo Slavery Songs Cangoma Calling Spirits and Rhythms of Freedom in Brazilian Jongo Slavery Songs Edited by Pedro Meira Monteiro Michael Stone luso-asio-afro-brazilian studies & theory 3 Editor Victor K. Mendes, University of Massachusetts Dartmouth Associate Editor Gina M. Reis, University of Massachusetts Dartmouth Editorial Board Hans Ulrich Gumbrecht, Stanford University Anna M. Klobucka, University of Massachusetts Dartmouth Pedro Meira Monteiro, Princeton University João Cezar de Castro Rocha, Universidade do Estado do Rio de Janeiro Phillip Rothwell, Rutgers University, New Brunswick Miguel Tamen, Universidade de Lisboa Claire Williams, University of Oxford Cover Design Inês Sena, Lisbon © 2013 The Authors We are thankful to the Centro de Pesquisa em História Social da Cultura (Cecult) and the Arquivo Edgar Leuenroth (AEL) at Unicamp for permission to reproduce the images in this book including the cover image. Library of Congress Cataloging-in-Publication Data Cangoma calling : spirits and rhythms of freedom in Brazilian jongo slavery songs / edited by Pedro Meira Monteiro ; Michael Stone. pages ; cm. -- (Luso-Asio-Afro-Brazilian studies & theory ; 3) Includes bibliographical references and index. ISBN 978-0-9814580-2-1 (alk. paper) 1. Jongos (Music)--History and criticism. 2. Blacks--Brazil--Music--History and criticism. 3. Music--Social aspects--Brazil. I. Monteiro, Pedro Meira. II. Stone, Michael. ML3575.B7C25 2013 781.62’96981--dc23 2012012085 Table of Contents Preface: A (Knotted) Stitch in Time, Weaving Connections Between Collections 7 Gage Averill Introduction: Jongos, the Creativity of the Enslaved and Beyond 11 Pedro Meira Monteiro and Michael Stone A Marvelous Journey 19 Stanley Stein Vassouras and the Sounds of Captivity in Southeast Brazil 25 Silvia Hunold Lara Memory Hanging by a Wire: Stanley J. -

Comhaltas Ceoltóirí Éireann (The Irish Musicians' Association) and the Politics of Musical Community in Irish Traditional Music
City University of New York (CUNY) CUNY Academic Works All Dissertations, Theses, and Capstone Projects Dissertations, Theses, and Capstone Projects 2-2015 Comhaltas Ceoltóirí Éireann (The Irish Musicians' Association) and the Politics of Musical Community in Irish Traditional Music Lauren Weintraub Stoebel Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/627 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] COMHALTAS CEOLTÓIRÍ ÉIREANN (THE IRISH MUSICIANS’ ASSOCIATION) AND THE POLITICS OF MUSICAL COMMUNITY IN IRISH TRADITIONAL MUSIC By LAUREN WEINTRAUB STOEBEL A dissertation submitted to the Graduate Faculty in Music in partial fulfillment of the requirements for the degree of Doctor of Philosophy, The City University of New York 2015 ii © 2015 LAUREN WEINTRAUB STOEBEL All Rights Reserved iii This manuscript has been read and accepted for the Graduate Faculty in Music in satisfaction of the dissertation requirement for the degree of Doctor of Philosophy. Peter Manuel______________________________ ________________ _________________________________________ Date Chair of Examining Committee Norman Carey_____________________________ ________________ _________________________________________ Date Executive Officer Jane Sugarman___________________________________________ Stephen Blum_____________________________________________ Sean Williams____________________________________________ Supervisory Committee THE CITY UNIVERSITY OF NEW YORK iv Abstract COMHALTAS CEOLTÓIRÍ ÉIREANN (THE IRISH MUSICIANS’ ASSOCIATION) AND THE POLITICS OF MUSICAL COMMUNITY IN IRISH TRADITIONAL MUSIC By LAUREN WEINTRAUB STOEBEL Advisor: Jane Sugarman This dissertation examines Comhaltas Ceoltóirí Éireann (The Irish Musicians’ Association) and its role in the politics of Irish traditional music communities.