Tion Analysis Using Both Host and Pathogen Genomes
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Genome Wide Association Study of Response to Interval and Continuous Exercise Training: the Predict‑HIIT Study Camilla J
Williams et al. J Biomed Sci (2021) 28:37 https://doi.org/10.1186/s12929-021-00733-7 RESEARCH Open Access Genome wide association study of response to interval and continuous exercise training: the Predict-HIIT study Camilla J. Williams1†, Zhixiu Li2†, Nicholas Harvey3,4†, Rodney A. Lea4, Brendon J. Gurd5, Jacob T. Bonafglia5, Ioannis Papadimitriou6, Macsue Jacques6, Ilaria Croci1,7,20, Dorthe Stensvold7, Ulrik Wislof1,7, Jenna L. Taylor1, Trishan Gajanand1, Emily R. Cox1, Joyce S. Ramos1,8, Robert G. Fassett1, Jonathan P. Little9, Monique E. Francois9, Christopher M. Hearon Jr10, Satyam Sarma10, Sylvan L. J. E. Janssen10,11, Emeline M. Van Craenenbroeck12, Paul Beckers12, Véronique A. Cornelissen13, Erin J. Howden14, Shelley E. Keating1, Xu Yan6,15, David J. Bishop6,16, Anja Bye7,17, Larisa M. Haupt4, Lyn R. Grifths4, Kevin J. Ashton3, Matthew A. Brown18, Luciana Torquati19, Nir Eynon6 and Jef S. Coombes1* Abstract Background: Low cardiorespiratory ftness (V̇O2peak) is highly associated with chronic disease and mortality from all causes. Whilst exercise training is recommended in health guidelines to improve V̇O2peak, there is considerable inter-individual variability in the V̇O2peak response to the same dose of exercise. Understanding how genetic factors contribute to V̇O2peak training response may improve personalisation of exercise programs. The aim of this study was to identify genetic variants that are associated with the magnitude of V̇O2peak response following exercise training. Methods: Participant change in objectively measured V̇O2peak from 18 diferent interventions was obtained from a multi-centre study (Predict-HIIT). A genome-wide association study was completed (n 507), and a polygenic predictor score (PPS) was developed using alleles from single nucleotide polymorphisms= (SNPs) signifcantly associ- –5 ated (P < 1 10 ) with the magnitude of V̇O2peak response. -

GCAT|Panel, a Comprehensive Structural Variant Haplotype Map of the Iberian Population from High-Coverage Whole-Genome Sequencing
bioRxiv preprint doi: https://doi.org/10.1101/2021.07.20.453041; this version posted July 21, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. GCAT|Panel, a comprehensive structural variant haplotype map of the Iberian population from high-coverage whole-genome sequencing Jordi Valls-Margarit1,#, Iván Galván-Femenía2,3,#, Daniel Matías-Sánchez1,#, Natalia Blay2, Montserrat Puiggròs1, Anna Carreras2, Cecilia Salvoro1, Beatriz Cortés2, Ramon Amela1, Xavier Farre2, Jon Lerga- Jaso4, Marta Puig4, Jose Francisco Sánchez-Herrero5, Victor Moreno6,7,8,9, Manuel Perucho10,11, Lauro Sumoy5, Lluís Armengol12, Olivier Delaneau13,14, Mario Cáceres4,15, Rafael de Cid2,*,† & David Torrents1,15,* 1. Life sciences dept, Barcelona Supercomputing Center (BSC), Barcelona, 08034, Spain. 2. Genomes for Life-GCAT lab Group, Institute for Health Science Research Germans Trias i Pujol (IGTP), Badalona, 08916, Spain. 3. Institute for Research in Biomedicine (IRB Barcelona), The Barcelona Institute of Science and Technology, 08028, Barcelona, Spain (current affiliation). 4. Institut de Biotecnologia i de Biomedicina, Universitat Autònoma de Barcelona, Bellaterra, Barcelona, 08193, Spain. 5. High Content Genomics and Bioinformatics Unit, Institute for Health Science Research Germans Trias i Pujol (IGTP), 08916, Badalona, Spain. 6. Catalan Institute of Oncology, Hospitalet del Llobregat, 08908, Spain. 7. Bellvitge Biomedical Research Institute (IDIBELL), Hospitalet del Llobregat, 08908, Spain. 8. CIBER Epidemiología y Salud Pública (CIBERESP), Madrid, 28029, Spain. 9. Universitat de Barcelona (UB), Barcelona, 08007, Spain. -

Gene Prioritization in Type 2 Diabetes Using Domain Interactions And
Sharma et al. BMC Genomics 2010, 11:84 http://www.biomedcentral.com/1471-2164/11/84 RESEARCH ARTICLE Open Access Gene prioritization in Type 2 Diabetes using domain interactions and network analysis Amitabh Sharma1†, Sreenivas Chavali1†, Rubina Tabassum1, Nikhil Tandon2, Dwaipayan Bharadwaj1* Abstract Background: Identification of disease genes for Type 2 Diabetes (T2D) by traditional methods has yielded limited success. Based on our previous observation that T2D may result from disturbed protein-protein interactions affected through disrupting modular domain interactions, here we have designed an approach to rank the candidates in the T2D linked genomic regions as plausible disease genes. Results: Our approach integrates Weight value (Wv) method followed by prioritization using clustering coefficients derived from domain interaction network. Wv for each candidate is calculated based on the assumption that disease genes might be functionally related, mainly facilitated by interactions among domains of the interacting proteins. The benchmarking using a test dataset comprising of both known T2D genes and non-T2D genes revealed that Wv method had a sensitivity and specificity of 0.74 and 0.96 respectively with 9 fold enrichment. The candidate genes having a Wv > 0.5 were called High Weight Elements (HWEs). Further, we ranked HWEs by using the network property-the clustering coefficient (Ci). Each HWE with a Ci < 0.015 was prioritized as plausible disease candidates (HWEc) as previous studies indicate that disease genes tend to avoid dense clustering (with an average Ci of 0.015). This method further prioritized the identified disease genes with a sensitivity of 0.32 and a specificity of 0.98 and enriched the candidate list by 6.8 fold. -

Downloaded Per Proteome Cohort Via the Web- Site Links of Table 1, Also Providing Information on the Deposited Spectral Datasets
www.nature.com/scientificreports OPEN Assessment of a complete and classifed platelet proteome from genome‑wide transcripts of human platelets and megakaryocytes covering platelet functions Jingnan Huang1,2*, Frauke Swieringa1,2,9, Fiorella A. Solari2,9, Isabella Provenzale1, Luigi Grassi3, Ilaria De Simone1, Constance C. F. M. J. Baaten1,4, Rachel Cavill5, Albert Sickmann2,6,7,9, Mattia Frontini3,8,9 & Johan W. M. Heemskerk1,9* Novel platelet and megakaryocyte transcriptome analysis allows prediction of the full or theoretical proteome of a representative human platelet. Here, we integrated the established platelet proteomes from six cohorts of healthy subjects, encompassing 5.2 k proteins, with two novel genome‑wide transcriptomes (57.8 k mRNAs). For 14.8 k protein‑coding transcripts, we assigned the proteins to 21 UniProt‑based classes, based on their preferential intracellular localization and presumed function. This classifed transcriptome‑proteome profle of platelets revealed: (i) Absence of 37.2 k genome‑ wide transcripts. (ii) High quantitative similarity of platelet and megakaryocyte transcriptomes (R = 0.75) for 14.8 k protein‑coding genes, but not for 3.8 k RNA genes or 1.9 k pseudogenes (R = 0.43–0.54), suggesting redistribution of mRNAs upon platelet shedding from megakaryocytes. (iii) Copy numbers of 3.5 k proteins that were restricted in size by the corresponding transcript levels (iv) Near complete coverage of identifed proteins in the relevant transcriptome (log2fpkm > 0.20) except for plasma‑derived secretory proteins, pointing to adhesion and uptake of such proteins. (v) Underrepresentation in the identifed proteome of nuclear‑related, membrane and signaling proteins, as well proteins with low‑level transcripts. -

HRC (M-14): Sc-138023
SAN TA C RUZ BI OTEC HNOL OG Y, INC . HRC (M-14): sc-138023 BACKGROUND APPLICATIONS HRC (histidine rich calcium binding protein), also known as sarcoplasmic retic - HRC (M-14) is recommended for detection of HRC of mouse and rat origin ulum histidine-rich calcium-binding protein or HCP, is a 699 amino acid that by Western Blotting (starting dilution 1:200, dilution range 1:100-1:1000), binds low-density lipoprotein with high affinity. As a high capacity calcium immunoprecipitation [1-2 µg per 100-500 µg of total protein (1 ml of cell binding protein, HRC regulates the sequestration and release of calcium in the lysate)], immunofluorescence (starting dilution 1:50, dilution range 1:50- lumen of the junctional sarcoplasmic reticulum (SR) of cardiac, skeletal and 1:500), immunohistochemistry (including paraffin-embedded sections) (start - smooth muscle. This mechanism may involve direct interaction between HRC ing dilution 1:50, dilution range 1:50-1:500) and solid phase ELISA (starting and the cytoplasmic domain of Triadin, an integral membrane protein of the dilution 1:30, dilution range 1:30-1:3000). SR. The gene encoding HRC maps to human chromosome 19q13.33 and mouse HRC (M-14) is also recommended for detection of HRC in additional species, chromosome 7 B4. including bovine. REFERENCES Suitable for use as control antibody for HRC siRNA (m): sc-146079, HRC shRNA Plasmid (m): sc-146079-SH and HRC shRNA (m) Lentiviral Particles: 1. Hofmann, S.L., et al. 1989. Purification of a sarcoplasmic reticulum protein sc-146079-V. that binds Ca 2+ and plasma lipoproteins. -

Maize GO Annotation - Methods, Evaluation, and Review (Maize-GAMER)
bioRxiv preprint doi: https://doi.org/10.1101/222836; this version posted November 21, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. Maize GO Annotation - Methods, Evaluation, and Review (maize-GAMER) Kokulapalan Wimalanathan1,2, Iddo Friedberg1,3, Carson M. Andorf4,5, and Carolyn J. Lawrence-Dill1,2,6,* 1Bioinformatics and Computational Biology, Iowa State University, Ames, IA 50011, USA 2Department of Genetics Development and Cell Biology, Iowa State University, Ames, IA 50011, USA 3Department of Veterinary Microbiology and Preventive Medicine, Iowa State University, Ames, IA 50011, USA 4USDA-ARS Corn Insects and Crop Genetics Research Unit, Iowa State University, Ames, IA 50011, USA 5Department of Computer Science, Iowa State University, Ames, IA 50011, USA 6Department of Agronomy, Iowa State University, Ames, IA 50011, USA *Correspondence to triffi[email protected] 1 bioRxiv preprint doi: https://doi.org/10.1101/222836; this version posted November 21, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. Summary We created a new high-coverage, robust, and reproducible functional annota- tion of maize protein coding genes based on Gene Ontology (GO) term assign- ments. Whereas the existing Phytozome and Gramene maize GO annotation sets only cover 41% and 56% of maize protein coding genes, respectively, this study provides annotations for 100% of the genes. -

393LN V 393P 344SQ V 393P Probe Set Entrez Gene
393LN v 393P 344SQ v 393P Entrez fold fold probe set Gene Gene Symbol Gene cluster Gene Title p-value change p-value change chemokine (C-C motif) ligand 21b /// chemokine (C-C motif) ligand 21a /// chemokine (C-C motif) ligand 21c 1419426_s_at 18829 /// Ccl21b /// Ccl2 1 - up 393 LN only (leucine) 0.0047 9.199837 0.45212 6.847887 nuclear factor of activated T-cells, cytoplasmic, calcineurin- 1447085_s_at 18018 Nfatc1 1 - up 393 LN only dependent 1 0.009048 12.065 0.13718 4.81 RIKEN cDNA 1453647_at 78668 9530059J11Rik1 - up 393 LN only 9530059J11 gene 0.002208 5.482897 0.27642 3.45171 transient receptor potential cation channel, subfamily 1457164_at 277328 Trpa1 1 - up 393 LN only A, member 1 0.000111 9.180344 0.01771 3.048114 regulating synaptic membrane 1422809_at 116838 Rims2 1 - up 393 LN only exocytosis 2 0.001891 8.560424 0.13159 2.980501 glial cell line derived neurotrophic factor family receptor alpha 1433716_x_at 14586 Gfra2 1 - up 393 LN only 2 0.006868 30.88736 0.01066 2.811211 1446936_at --- --- 1 - up 393 LN only --- 0.007695 6.373955 0.11733 2.480287 zinc finger protein 1438742_at 320683 Zfp629 1 - up 393 LN only 629 0.002644 5.231855 0.38124 2.377016 phospholipase A2, 1426019_at 18786 Plaa 1 - up 393 LN only activating protein 0.008657 6.2364 0.12336 2.262117 1445314_at 14009 Etv1 1 - up 393 LN only ets variant gene 1 0.007224 3.643646 0.36434 2.01989 ciliary rootlet coiled- 1427338_at 230872 Crocc 1 - up 393 LN only coil, rootletin 0.002482 7.783242 0.49977 1.794171 expressed sequence 1436585_at 99463 BB182297 1 - up 393 -

Understanding the Functional Role of Genistein in the Bone Differentiation
www.nature.com/scientificreports Correction: Author Correction OPEN Understanding the functional role of genistein in the bone diferentiation in mouse Received: 16 June 2017 Accepted: 7 February 2018 osteoblastic cell line MC3T3-E1 by Published online: 19 February 2018 RNA-seq analysis Myungsuk Kim1,2, Jisun Lim3, Jung-Hee Lee3, Kyung-Mi Lee1,2, Suji Kim4, Kye Won Park4, Chu Won Nho1,2 & Yoon Shin Cho3 Genistein, a phyto-estrogen, can potentially replace endogenous estrogens in postmenopausal women, but the underlying molecular mechanisms remain incompletely understood. To obtain insight into the efect of genistein on bone diferentiation, RNA sequencing (RNA-seq) analysis was used to detect diferentially expressed genes (DEGs) in genistein-treated vs. untreated MC3T3-E1 mouse osteoblastic cells. Osteoblastic cell diferentiation was monitored by measuring osteoblast diferentiation factors (ALP production, bone mineralization, and expression of osteoblast diferentiation markers). From RNA-seq analysis, a total of 132 DEGs (including 52 up-regulated and 80 down-regulated genes) were identifed in genistein-treated cells (FDR q-value < 0.05 and fold change > 1.5). KEGG pathway and Gene Ontology (GO) enrichment analyses were performed to estimate the biological functions of DEGs and demonstrated that these DEGs were highly enriched in functions related to chemotactic cytokines. The functional relevance of DEGs to genistein-induced osteoblastic cell diferentiation was further evaluated by siRNA-mediated knockdown in MC3T3-E1 cells. These siRNA knockdown experiments (of the DEGs validated by real-time qPCR) demonstrated that two up-regulated genes (Ereg and Efcab2) enhance osteoblastic cell diferentiation, while three down-regulated genes (Hrc, Gli, and Iftm5) suppress the diferentiation. -

Comparison of Human Chromosome 19Q13 and Syntenic Region On
European Journal of Human Genetics (2010) 18, 442–447 & 2010 Macmillan Publishers Limited All rights reserved 1018-4813/10 $32.00 www.nature.com/ejhg ARTICLE Comparison of human chromosome 19q13 and syntenic region on mouse chromosome 7 reveals absence, in man, of 11.6 Mb containing four mouse calcium-sensing receptor-related sequences: relevance to familial benign hypocalciuric hypercalcaemia type 3 Fadil M Hannan1, M Andrew Nesbit1, Jeremy JO Turner1,2, Joanna M Stacey1, Luisella Cianferotti3, Paul T Christie1, Arthur D Conigrave4, Michael P Whyte5,6 and Rajesh V Thakker*,1 Familial benign hypocalciuric hypercalcaemia (FBHH) is a genetically heterogeneous disorder that consists of three designated types, FBHH1, FBHH2 and FBHH3, whose chromosomal locations are 3q21.1, 19p and 19q13, respectively. FBHH1 is caused by mutations of a calcium-sensing receptor (CaSR), but the abnormalities underlying FBHH2 and FBHH3 are unknown. FBHH3, also referred to as the Oklahoma variant (FBHHOk), has been mapped to a 12cM interval, flanked by D19S908 and D19S866. To refine the location of FBHH3, we pursued linkage studies using 24 polymorphic loci. Our results establish a linkage between FBHH3 and 17 of these loci, and indicate that FBHH3 is located in a 4.1 Mb region flanked centromerically by D19S112 and telomerically by rs245111, which in the syntenic region on mouse chromosome 7 contains four Casr-related sequences (Gprc2a-rss). However, human homologues of these Gprc2a-rss were not found and a comparative analysis of the 22.0 Mb human and 39.3 Mb mouse syntenic regions showed evolutionary conservation of two segments that were inverted with loss from the human genome of 11.6 Mb that contained the four Gprc2a-rss. -
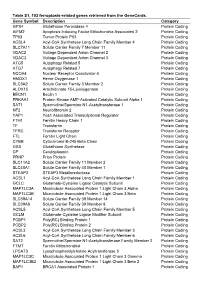
Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein -

Rabbit Anti-HRC/FITC Conjugated Antibody
SunLong Biotech Co.,LTD Tel: 0086-571- 56623320 Fax:0086-571- 56623318 E-mail:[email protected] www.sunlongbiotech.com Rabbit Anti-HRC/FITC Conjugated antibody SL17387R-FITC Product Name: Anti-HRC/FITC Chinese Name: FITC标记的HRC蛋白抗体 HCP; HRC; HRC histidine rich calcium binding protein; MGC133236; Sarcoplasmic Alias: reticulum histidine-rich calcium-binding protein; SRCH_HUMAN. Organism Species: Rabbit Clonality: Polyclonal React Species: Human, ICC=1:50-200IF=1:50-200 Applications: not yet tested in other applications. optimal dilutions/concentrations should be determined by the end user. Molecular weight: 77kDa Form: Lyophilized or Liquid Concentration: 1mg/ml immunogen: KLH conjugated synthetic peptide derived from human HRC Lsotype: IgG Purification: affinity purified by Protein A Storage Buffer: 0.01M TBS(pH7.4) with 1% BSA, 0.03% Proclin300 and 50% Glycerol. Storewww.sunlongbiotech.com at -20 °C for one year. Avoid repeated freeze/thaw cycles. The lyophilized antibody is stable at room temperature for at least one month and for greater than a year Storage: when kept at -20°C. When reconstituted in sterile pH 7.4 0.01M PBS or diluent of antibody the antibody is stable for at least two weeks at 2-4 °C. background: HRC is a 699 amino acid that binds low-density lipoprotein with high affinity. As a high capacity calcium binding protein, HRC regulates the sequestration and release of calcium in the lumen of the junctional sarcoplasmic reticulum (SR) of cardiac, skeletal Product Detail: and smooth muscle. This mechanism may involve direct interaction between HRC and the cytoplasmic domain of Triadin, an integral membrane protein of the SR. -

Gene-Based Analysis in HRC Imputed Genome Wide
bioRxiv preprint doi: https://doi.org/10.1101/374876; this version posted July 23, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Gene-Based Analysis in HRC Imputed Genome Wide Association Data Identifies Three Novel Genes For Alzheimer’s Disease Emily Baker1, Rebecca Sims1, Ganna Leonenko1, Aura Frizzati1, Janet Harwood1, Detelina Grozeva1, GERAD/PERADES+, IGAP consortia+, Kevin Morgan2, Peter Passmore3, Clive Holmes4, John Powell5, Carol Brayne6, Michael Gill7, Simon Mead8, Reiner Heun9, Paola Bossù10, Gianfranco Spalletta11, Alison Goate12, Carlos Cruchaga13, Cornelia van Duijn14, Wolfgang Maier9,15, Alfredo Ramirez9,16, Lesley Jones1, John Hardy17, Dobril Ivanov18, Matthew Hill18, Peter Holmans1, Nicholas Allen18, Paul Morgan18, Julie Williams1,18*, Valentina Escott-Price1,18* 1Medical Research Council Centre for Neuropsychiatric Genetics and Genomics, Division of Psychological Medicine and Clinical Neurosciences, Cardiff University, UK, 2Institute of Genetics, Queens Medical Centre, University of Nottingham, UK, 3Ageing Group, Centre for Public Health, School of Medicine, Dentistry and Biomedical Sciences, Queens University Belfast, UK, 4Division of Clinical Neurosciences, School of Medicine, University of Southampton, Southampton, UK, 5Kings College London, Institute of Psychiatry, Department of Neuroscience, De Crespigny Park, Denmark Hill, London, 6Institute of Public Health, University of Cambridge, Cambridge,