Not Set Pdfsubject
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
Messier Plus Marathon Text
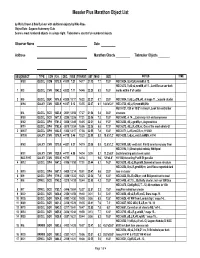
Messier Plus Marathon Object List by Wally Brown & Bob Buckner with additional objects by Mike Roos Object Data - Saguaro Astronomy Club Score is most numbered objects in a single night. Tiebreaker is count of un-numbered objects Observer Name Date Address Marathon Obects __________ Tiebreaker Objects ________ SEQ OBJECT TYPE CON R.A. DEC. RISE TRANSIT SET MAG SIZE NOTES TIME M 53 GLOCL COM 1312.9 +1810 7:21 14:17 21:12 7.7 13.0' NGC 5024, !B,vC,iR,vvmbM,st 12.. NGC 5272, !!,eB,vL,vsmbM,st 11.., Lord Rosse-sev dark 1 M 3 GLOCL CVN 1342.2 +2822 7:11 14:46 22:20 6.3 18.0' marks within 5' of center 2 M 5 GLOCL SER 1518.5 +0205 10:17 16:22 22:27 5.7 23.0' NGC 5904, !!,vB,L,eCM,eRi, st mags 11...;superb cluster M 94 GALXY CVN 1250.9 +4107 5:12 13:55 22:37 8.1 14.4'x12.1' NGC 4736, vB,L,iR,vsvmbM,BN,r NGC 6121, Cl,8 or 10 B* in line,rrr, Look for central bar M 4 GLOCL SCO 1623.6 -2631 12:56 17:27 21:58 5.4 36.0' structure M 80 GLOCL SCO 1617.0 -2258 12:36 17:21 22:06 7.3 10.0' NGC 6093, st 14..., Extremely rich and compressed M 62 GLOCL OPH 1701.2 -3006 13:49 18:05 22:21 6.4 15.0' NGC 6266, vB,L,gmbM,rrr, Asymmetrical M 19 GLOCL OPH 1702.6 -2615 13:34 18:06 22:38 6.8 17.0' NGC 6273, vB,L,R,vCM,rrr, One of the most oblate GC 3 M 107 GLOCL OPH 1632.5 -1303 12:17 17:36 22:55 7.8 13.0' NGC 6171, L,vRi,vmC,R,rrr, H VI 40 M 106 GALXY CVN 1218.9 +4718 3:46 13:23 22:59 8.3 18.6'x7.2' NGC 4258, !,vB,vL,vmE0,sbMBN, H V 43 M 63 GALXY CVN 1315.8 +4201 5:31 14:19 23:08 8.5 12.6'x7.2' NGC 5055, BN, vsvB stell. -

Central Coast Astronomy Virtual Star Party January 16Th 7Pm Pacific
Central Coast Astronomy Virtual Star Party January 16th 7pm Pacific Welcome to our Virtual Star Gazing session! We’ll be focusing on objects you can see with binoculars or a small telescope, so after our session, you can simply walk outside, look up, and understand what you’re looking at. CCAS President Aurora Lipper and astronomer Kent Wallace will bring you a virtual “tour of the night sky” where you can discover, learn, and ask questions as we go along! All you need is an internet connection. You can use an iPad, laptop, computer or cell phone. When 7pm on Saturday night rolls around, click the link on our website to join our class. CentralCoastAstronomy.org/stargaze Before our session starts: Step 1: Download your free map of the night sky: SkyMaps.com They have it available for Northern and Southern hemispheres. Step 2: Print out this document and use it to take notes during our time on Saturday. This document highlights the objects we will focus on in our session together. Celestial Objects: Moon: The moon is 3 days past new, which is really good for star gazing. Be sure to look at the moon tonight with your naked eyes and/or binoculars! Mercury is rising into the western sky and may be a good target near the end of the month. Mars is up high but is shrinking in size as the weeks progress. *Image credit: all astrophotography images are courtesy of NASA unless otherwise noted. All planetarium images are courtesy of Stellarium. Central Coast Astronomy CentralCoastAstronomy.org Page 1 Main Focus for the Session: 1. -

407 a Abell Galaxy Cluster S 373 (AGC S 373) , 351–353 Achromat
Index A Barnard 72 , 210–211 Abell Galaxy Cluster S 373 (AGC S 373) , Barnard, E.E. , 5, 389 351–353 Barnard’s loop , 5–8 Achromat , 365 Barred-ring spiral galaxy , 235 Adaptive optics (AO) , 377, 378 Barred spiral galaxy , 146, 263, 295, 345, 354 AGC S 373. See Abell Galaxy Cluster Bean Nebulae , 303–305 S 373 (AGC S 373) Bernes 145 , 132, 138, 139 Alnitak , 11 Bernes 157 , 224–226 Alpha Centauri , 129, 151 Beta Centauri , 134, 156 Angular diameter , 364 Beta Chamaeleontis , 269, 275 Antares , 129, 169, 195, 230 Beta Crucis , 137 Anteater Nebula , 184, 222–226 Beta Orionis , 18 Antennae galaxies , 114–115 Bias frames , 393, 398 Antlia , 104, 108, 116 Binning , 391, 392, 398, 404 Apochromat , 365 Black Arrow Cluster , 73, 93, 94 Apus , 240, 248 Blue Straggler Cluster , 169, 170 Aquarius , 339, 342 Bok, B. , 151 Ara , 163, 169, 181, 230 Bok Globules , 98, 216, 269 Arcminutes (arcmins) , 288, 383, 384 Box Nebula , 132, 147, 149 Arcseconds (arcsecs) , 364, 370, 371, 397 Bug Nebula , 184, 190, 192 Arditti, D. , 382 Butterfl y Cluster , 184, 204–205 Arp 245 , 105–106 Bypass (VSNR) , 34, 38, 42–44 AstroArt , 396, 406 Autoguider , 370, 371, 376, 377, 388, 389, 396 Autoguiding , 370, 376–378, 380, 388, 389 C Caldwell Catalogue , 241 Calibration frames , 392–394, 396, B 398–399 B 257 , 198 Camera cool down , 386–387 Barnard 33 , 11–14 Campbell, C.T. , 151 Barnard 47 , 195–197 Canes Venatici , 357 Barnard 51 , 195–197 Canis Major , 4, 17, 21 S. Chadwick and I. Cooper, Imaging the Southern Sky: An Amateur Astronomer’s Guide, 407 Patrick Moore’s Practical -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

The Bennett Catalogue
The Bennett Catalogue www.macastro.org.au Catalogue Numbers Type R.A. Dec. U2000 Con. Ben 1 NGC 55 Gal 0:14:54 -39:11 386 Scl Ben 2 NGC 104 GC 0:24:06 -72:05 440 Tuc Ben 3 NGC 247 Gal 0:47:06 -20:46 306 Cet Ben 4 NGC 253 Gal 0:47:36 -25:17 306 Scl Ben 5 NGC 288 GC 0:52:48 -26:35 307 Scl Ben 6 NGC 300 Gal 0:54:54 -37:41 351 Scl Ben 7 NGC 362 GC 1:03:12 -70:51 441 Tuc Ben 8 NGC 613 Gal 1:34:18 -29:25 352 Scl Ben 9 NGC 1068 Gal 2:42:42 -00:01 220 Cet Ben 10 NGC 1097 Gal 2:46:18 -30:17 354 For Ben 10a NGC 1232 Gal 3:09:48 -20:35 311 Eri Ben 11 NGC 1261 GC 3:12:18 -55:13 419 Hor Ben 12 NGC 1291 Gal 3:17:18 -41:08 390 Eri Ben 13 NGC 1313 Gal 3:18:18 -66:30 443 Ret Ben 14 NGC 1316 Gal 3:22:42 -37:12 355 For Ben 14a NGC 1350 Gal 3:31:06 -33:38 355 For Ben 15 NGC 1360 PN 3:33:18 -25:51 312 For Ben 16 NGC 1365 Gal 3:33:36 -36:08 355 For Ben 17 NGC 1380 Gal 3:36:30 -34:59 355 For Ben 18 NGC 1387 Gal 3:37:00 -35:31 355 For Ben 19 NGC 1399 Gal 3:38:30 -35:27 355 For Ben 19a NGC 1398 Gal 3:38:54 -26:20 312 For Ben 20 NGC 1404 Gal 3:38:54 -35:35 355 Eri Ben 21 NGC 1433 Gal 3:42:00 -47:13 391 Hor Ben 21a NGC 1512 Gal 4:03:54 -43:21 391 Hor Ben 22 NGC 1535 PN 4:14:12 -12:44 268 Eri Ben 23 NGC 1549 Gal 4:15:42 -55:36 420 Dor Ben 24 NGC 1553 Gal 4:16:12 -55:47 420 Dor Ben 25 NGC 1566 Gal 4:20:00 -54:56 420 Dor Ben 25a NGC 1617 Gal 4:31:42 -54:36 421 Dor Ben 26 NGC 1672 Gal 4:45:42 -59:15 421 Dor Ben 27 NGC 1763 BN 4:56:48 -66:24 444 Dor Ben 28 NGC 1783 GC 4:58:54 -66:00 444 Dor Ben 29 NGC 1792 Gal 5:05:12 -37:59 358 Col -

One of the Most Useful Accessories an Amateur Can Possess Is One of the Ubiquitous Optical Filters
One of the most useful accessories an amateur can possess is one of the ubiquitous optical filters. Having been accessible previously only to the professional astronomer, they came onto the marker relatively recently, and have made a very big impact. They are useful, but don't think they're the whole answer! They can be a mixed blessing. From reading some of the advertisements in astronomy magazines you would be correct in thinking that they will make hitherto faint and indistinct objects burst into vivid observ ability. They don't. What the manufacturers do not mention is that regardless of the filter used, you will still need dark and transparent skies for the use of the filter to be worthwhile. Don't make the mistake of thinking that using a filter from an urban location will always make objects become clearer. The first and most immediately apparent item on the downside is that in all cases the use of a filter reduces the amount oflight that reaches the eye, often quite sub stantially. The brightness of the field of view and the objects contained therein is reduced. However, what the filter does do is select specific wavelengths of light emitted by an object, which may be swamped by other wavelengths. It does this by suppressing the unwanted wavelengths. This is particularly effective in observing extended objects such as emission nebulae and planetary nebulae. In the former case, use a filter that transmits light around the wavelength of 653.2 nm, which is the spectral line of hydrogen alpha (Ha), and is the wavelength oflight respons ible for the spectacular red colour seen in photographs of emission nebulae. -

ASEM Newsletter December2015
ASEM Newsletter December2015 Comet C/2013 US10 Catalina December 1st, 2015 image from Gregg Ruppel December Calendar Social December 3 – 7-9pm Beginner Meeting @ Weldon Springs Interpretive Center, 7295 HWY 94 South, St. Charles, MO 63304 December 12 – Monthly Meeting. 5pm Open House, hors d’oeuvres @ Weldon Springs Interpretive Center, 7295 HWY 94 South, St. Charles, MO 63304. 6pm ham dinner provided by Marv and Barb Stewart followed by monthly meeting at 7pm. Complimentary dishes and desserts are welcome. Carla Kamp is turning over hospitality hosting duties with the January meeting. December 22- 7pm DigitalSIG Astrophoto group meeting Weldon Spring, 7295 Highway 94 South, St. Charles, MO 63304. Note this is the FOURTH Tuesday for just this month. We’ll go back to the 3rd Tuesday in January. December 23- 7PM DIY-ATMSIG Weldon Spring, 7295 Highway 94 South, St. Charles, MO 63304 December 4, 11, 18, 25- 7 pm start times Broemmelsiek Park Public viewing, weather permitting. ASTRONOMICAL DELIGHTS If you’re very careful, on December 7 a very old crescent moon will occult Venus in daylight, late morning. You’ll need to look to the west of the sun-don’t catch the sun in your binoculars- around 11:10 or so for the disappearance on the bright side of the moon. Start your search before 11am so you know where Venus and the moon are. Venus will be occulted for about 90 minutes. There’s a really good lunar libration on December 21 at the north Polar region. Good night to poke around the north polar landscape craters that are not normally discernible. -

The Hot White Dwarf in the Peculiar Binary Nucleus of the Planetary Nebula EGB 6? K
A&A 616, A73 (2018) Astronomy https://doi.org/ 10.1051/0004-6361/201833200 & © ESO 2018 Astrophysics The hot white dwarf in the peculiar binary nucleus of the planetary nebula EGB 6? K. Werner1, T. Rauch1, and J. W. Kruk2 1 Institute for Astronomy and Astrophysics, Kepler Center for Astro and Particle Physics, Eberhard Karls University, Sand 1, 72076 Tübingen, Germany e-mail: [email protected] 2 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA Received 10 April 2018 / Accepted 14 May 2018 ABSTRACT EGB 6 is an extended, faint old planetary nebula (PN) with an enigmatic nucleus. The central star (PG 0950+139) is a hot DAOZ-type white dwarf (WD). An unresolved, compact emission knot was discovered to be located 000: 166 away from the WD and it was shown to be centered around a dust-enshrouded low-luminosity star. It was argued that the dust disk and evaporated gas (photoionized by the hot WD) around the companion are remnants of a disk formed by wind material captured from the WD progenitor when it was an asymptotic giant branch (AGB) star. In this paper, we assess the hot WD to determine its atmospheric and stellar parameters. We performed a model-atmosphere analysis of ultraviolet (UV) and optical spectra. We found Teff = 105 000 5000 K, log g = 7:4 0:4, and a solar helium abundance (He = 0:25 0:1, mass fraction). We measured the abundances of ten more± species (C, N, O,± F, Si, P, S, Ar, Fe, Ni) and found essentially solar± abundance values, indicating that radiation-driven wind mass-loss, with a theoretical ˙ +1:1 rate of log(M=M /yr) = 11:0 0:8, prevents the gravitational separation of elements in the photosphere. -

A Catalogue of Integrated H-Alpha Fluxes for 1258 Galactic Planetary Nebulae
Mon. Not. R. Astron. Soc. 000, 1–49 (2012) Printed 13 November 2012 (MN LATEX style file v2.2) A catalogue of integrated Hα fluxes for 1,258 Galactic planetary nebulae David J. Frew1,2⋆, Ivan S. Bojiˇci´c1,2,3 and Q.A. Parker1,2,3 1Department of Physics and Astronomy, Macquarie University, NSW 2109, Australia 2Research Centre in Astronomy, Astrophysics and Astrophotonics, Macquarie University, NSW 2109, Australia 3Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia Accepted ; Received ; in original form ABSTRACT We present a catalogue of new integrated Hα fluxes for 1258 Galactic planetary nebulae (PNe), with the majority, totalling 1234, measured from the Southern Hα Sky Survey Atlas (SHASSA) and/or the Virginia Tech Spectral-line Survey (VTSS). Aperture photometry on the continuum-subtracted digital images was performed to extract Hα+[N ii] fluxes in the case of SHASSA, and Hα fluxes from VTSS. The [N ii] contribution was then deconvolved from the SHASSA flux using spectrophotometric data taken from the literature or derived by us. Comparison with previous work shows that the flux scale presented here has no significant zero-point error. Our catalogue is the largest compilation of homogeneously derived PN fluxes in any waveband yet measured, and will be an important legacy and fresh benchmark for the community. Amongst its many applications, it can be used to determine statistical distances for these PNe, determine new absolute magnitudes for delineating the faint end of the PN luminosity function, provide baseline data for photoionization and hydrodynam- ical modelling, and allow better estimates of Zanstra temperatures for PN central stars with accurate optical photometry. -

7.5 X 12.5 Long Title.P65
Cambridge University Press 978-0-521-89936-9 - Cosmic Challenge: The Ultimate Observing List for Amateurs Philip S. Harrington Index More information Index 16+17 Draconis, 92–3 CGCG 89–56, 369 IC 4614, 327 30 Arietis, 113 CGCG 89–62, 369 IC 4616, 326 3C273, 141–2 Cocoon Nebula, 161–3 IC 4617, 326 61 Cygni, 159–60 Collinder 470, 163 IC 4732, 330–1 Abell 12, 358–9 Copeland’s Septet, 380–1 IC 4997, 248–9 Abell 33, 308–9 Crab Nebula, 118–19 IC 5067, 104 Abell 36, 319–20 IC 5070, 104 Abell 70, 335–6 Dark Horse Nebula, 41–3 IC 5146, 161–3 Abell Galaxy Cluster 373, 271–3 Dawes’ Limit, 13 IC 5217, 252–3 Abell Galaxy Cluster 426, 355–7 Deer Lick Group, 254–6 IRAS 18333–2357. See PK 9–7.1 Abell Galaxy Cluster 1060, 313–16 Double Cross. See Leo Trio Izar, 145–6 Abell Galaxy Cluster 1367, 382–6 double stars (table), 463–6 Abell Galaxy Cluster 1656, 387–91 Dumbbell Nebula, 97 Jonckheere 320, 274–5 Abell Galaxy Cluster 2065, 392–4 Jonckheere 900, 186–7 Abell Galaxy Cluster 2151, 398–401 Einstein’s Cross, 420–2 Jones-Emberson 1. See PK 164+31.1 Alcor. See Mizar Elephant’s Trunk Nebula, 418–19 Andromeda Galaxy, 51–3 Epsilon Bootis.¨ See Izar K648. See Pease 1 Antennae, The, 228–9 exit pupil, 15 Kratz’s Cascade, 281 Arp 41, 352–4 eye, human, 2 Arp 77, 349–51 eyepieces, 14–17 Lambda Arietis, 113 Arp 82, 362–3 apparent field of view, 16 Lambda Cassiopeiae, 261–3 averted vision, 3 color, 17 Leo I, 371–3 deep-sky, 17–20 Leo II, 374–5 Barnard 33, 184–5 filters, 17–20 Leo Trio, 88–9 Barnard 59. -
For – Objektauswahl NGC
For – Objektauswahl NGC NGC 686 NGC 857 NGC 1210 NGC 1326 NGC 1366 NGC 1385 NGC 1428 NGC 689 NGC 897 NGC 1217 NGC 1327 NGC 1387 NGC 1459 NGC 696 NGC 922 NGC 1255 NGC 1336 NGC 1371 NGC 1396 NGC 698 NGC 964 NGC 1288 NGC 1339 NGC 1373 NGC 1398 NGC 727 NGC 986 NGC 1292 NGC 1341 NGC 1374 NGC 1399 NGC 749 NGC 1049 NGC 1302 NGC 1344 NGC 1375 NGC 1404 NGC 775 NGC 1079 NGC 1306 NGC 1350 NGC 1379 NGC 1406 NGC 823 NGC 1097 NGC 1310 NGC 1351 NGC 1380 NGC 1412 NGC 824 NGC 1165 NGC 1316 NGC 1360 NGC 1381 NGC 1425 NGC 854 NGC 1201 NGC 1317 NGC 1365 NGC 1382 NGC 1427 Zur Objektauswahl: Nummer anklicken Sternbild- Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken For Sternbildübersichtskarte Auswahl NGC 686_689_775 Aufsuchkarte Auswahl NGC 696_698_727_749 Aufsuchkarte Auswahl NGC 823 Aufsuchkarte Auswahl NGC 824_854_857_897 Aufsuchkarte Auswahl NGC 922 Aufsuchkarte Auswahl NGC 964_986 Aufsuchkarte Auswahl NGC 1049 Aufsuchkarte Auswahl NGC 1079_1097 Aufsuchkarte Auswahl NGC 1165 Aufsuchkarte Auswahl NGC 1201_1210_1255 Aufsuchkarte Auswahl NGC 1217_1310_1316_1317_1326 Aufsuchkarte Auswahl NGC 1288_1339_1344_1350_1366_1406_1425 Aufsuchkarte Auswahl NGC 1292_1302_06_27_60_71_85_98_1412_59 Aufsuchkarte Auswahl NGC 1336_1341_1365 Aufsuchkarte Auswahl NGC 1351_73_74_75_79_80_81_82_87_96_99_1404_27_28Aufsuchkarte Auswahl NGC 686 Übersichtskarte Aufsuch- Auswahl karte NGC 689 Übersichtskarte Aufsuch- Auswahl karte NGC 696_698 Übersichtskarte Aufsuch- Auswahl karte NGC 727 Übersichtskarte Aufsuch-