DOCSLIB.ORG

A Derivation of Modified Newtonian Dynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Derivation of Modified Newtonian Dynamics Journal of The Korean Astronomical Society http://dx.doi.org/10.5303/JKAS.2013.46.2.93 46: 93 ∼ 96, 2013 April ISSN:1225-4614 c 2013 The Korean Astronomical Society. All Rights Reserved. http://jkas.kas.org A DERIVATION OF MODIFIED NEWTONIAN DYNAMICS Sascha Trippe Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea E-mail : [email protected] (Received February 14, 2013; Revised March 20, 2013; Accepted March 29, 2013) ABSTRACT Modified Newtonian Dynamics (MOND) is a possible solution for the missing mass problem in galac- tic dynamics; its predictions are in good agreement with observations in the limit of weak accelerations. However, MOND does not derive from a physical mechanism and does not make predictions on the transitional regime from Newtonian to modified dynamics; rather, empirical transition functions have to be constructed from the boundary conditions and comparisons with observations. I compare the formalism of classical MOND to the scaling law derived from a toy model of gravity based on virtual massive gravitons (the “graviton picture”) which I proposed recently. I conclude that MOND naturally derives from the “graviton picture” at least for the case of non-relativistic, highly symmetric dynamical systems. This suggests that – to first order – the “graviton picture” indeed provides a valid candidate for the physical mechanism behind MOND and gravity on galactic scales in general. Key words : Gravitation — Galaxies: kinematics and dynamics −10 −2 1. INTRODUCTION where x = ac/am, am ≈ 10 ms is Milgrom’s con- stant, and µ(x)isa transition function with the asymp- “ It is worth remembering that all of the discus- totic behavior µ(x) → 1 for x ≫ 1 and µ(x) → x for sion [on dark matter] so far has been based on x ≪ 1. The first limiting case corresponds to stan- the premise that Newtonian gravity and general dard Newtonian dynamics. The second limiting case relativity are correct on large scales. In fact, 4 ≈ there is little or no direct evidence that conven- leads to vc GM0 am = const.; this explains the tional theories of gravity are correct on scales asymptotic flattening of galactic rotation curves, the Tully-Fisher/Faber-Jackson relations, and (via division much larger than a parsec or so. ” 2 — Binney & Tremaine (1987), Ch. 10.4, p. 635 by r ) the surface brightness–acceleration relation of galaxies (see, e.g., Famaey & McGaugh 2012 for a re- Since the seminal works by Zwicky (1933) and Ru- cent review). bin et al. (1980), it has become evident (e.g., Binney Despite its success, MOND is obviously incomplete. & Tremaine 1987; Sanders 1990) that the dynamical Firstly, it does not derive from a physical mechanism masses of galaxies and galaxy clusters exceed their lu- a priori. Second, even though it provides the correct minous (baryonic) masses by up to one order of mag- limiting cases by construction, MOND does not provide nitude – the well-known missing mass problem. A pos- µ(x) itself and makes no prediction on the transitional sible solution is provided by Modified Newtonian Dy- regime from Newtonian to modified dynamics. This is namics (MOND) which postulates a modification of especially unfortunate given the fact that the transi- the classical Newtonian laws of inertia and/or gravity tional regime has been explored by observations: the in the limit of weak accelerations (Milgrom 1983a,b,c; empirical mass discrepancy–acceleration (MDA) rela- Bekenstein & Milgrom 1984; Sanders & McGaugh 2002; tion (McGaugh 2004) shows that the ratio Mtot/M0 Bekenstein 2006; Ferreira & Starkman 2009; Famaey & (the mass discrepancy) is a characteristic function of McGaugh 2012). Assuming a test particle on a circu- the accelerations ac and gn; here Mtot is the total dy- 2 lar orbit around a baryonic mass M0 at distance r with namical mass given by ac = GMtot/r . If a prediction ∗ circular speed vc, MOND relates the centripetal ac- 2 for µ(x) was available, it could be tested by compari- celeration ac = vc /r and the Newtonian acceleration 2 son to the empirical MDA relation in a straightforward gn = GM0/r , with G being Newton’s constant, as manner. gn Recently, I proposed a scheme for gravitational in- = µ(x) (1) teraction on galactic scales (the “graviton picture”) ac which is based on the ad-hoc assumption that grav- ity is mediated by virtual massive gravitons that obey ∗For simplicity, I only regard absolute values of velocities and certain reasonable rules of interaction (Trippe 2013). accelerations; the orientations are evident from the assumed geometry. The “graviton picture” predicts a theoretical MDA re- – 93 – 94 S. TRIPPE lation which is in good agreement with observations; it where a0 is a constant of the dimension of an accel- comprises expressions for limiting cases that agree with eration. The limiting case ac ≫ 8πa0 corresponds those of MOND (and likewise agree with observations). to the usual Newtonian dynamics. The limiting case 4 The present work follows up on, and amends, Trippe ac ≪ 8πa0 leads to vc ≈ 8π GM0 a0 = const.; from (2013). I realized only after publication of Trippe comparison to the corresponding MOND result we find (2013) an additional consequence of my toy model of am ≡ 8πa0. gravity introduced there: A comparison of classical In contrast to MOND, the “graviton picture” com- MOND and “graviton picture” shows that MOND nat- prises a scaling law for the transitional regime from urally derives from the “graviton picture” at least for Newtonian to modified dynamics (Eq. 5) a priori. In the case of non-relativistic, highly symmetric dynam- analogy to Eq. 1 we can define a transition function ical systems. This comparison is the subject of the present work. −1 gn M0 1 ξ(x)= = = 1+ (6) ac Mtot x 2. ANALYSIS with x = ac/am as before. This results in 2.1 Transition Functions in MOND x Eq. 1 provides the defining properties of MOND; the ξ(x)= = µ1(x) . (7) transition function µ(x) is constrained by (1) limiting 1+ x cases that have to be consistent with observations (2) As we see, the transition function ξ(x) provided by the the condition that xµ(x) increases monotonically with “graviton picture” is identical to the MOND transition x (Famaey & McGaugh 2012). These conditions are function µn(x) for n = 1. fulfilled (e.g., Milgrom 1983a; Famaey & Binney 2005; Furthermore, we can define an inverse transition Famaey & McGaugh 2012) by the set of functions function in analogy to Eq. 3 as x µn(x)= 1 ; n =1, 2, 3, ... (2) Mtot ac gn x (1 + xn) /n ζ = = −→ y = = . (8) M0 gn am ζ Alternatively, one may re-write Eq. 1 as Via Eq. 5 this leads to the quadratic equation ac = ν(y) (3) 2 1 gn ζ − ζ − =0 . (9) y −1 2 where y = gn/am; ν(y) → 1 for y ≫ 1 and ν(y) → y / for y ≪ 1. For reasons analogous to those for the case Solving this expression for ζ and ignoring the unphys- of µ(x), a set of valid transition functions is given by ical negative root, we find (Famaey & McGaugh 2012) 1 2 1 4 / 1 ζ(y)= 1+ 1+ = ν1(y) . (10) 1/2 /n 2 y 1 4 " # ν (y)= 1+ 1+ . (4) n 2 yn ( " #) In this case, the transition function ζ(y) provided by the “graviton picture” is identical to the MOND transi- Comparison to the empirical MDA relation suggests tion function νn(y) for n = 1. I illustrate the functions n = 1 or n = 2 (Kroupa 2012). Nevertheless, none −1 −1 of these scaling relations follows from first principles: ξ (x) = µ1 (x) and ζ(y) = ν1(y) in Fig. 1; the di- technically, arbitrary alternative transition functions agrams should be compared to Fig. 10 of Famaey & can be constructed from comparison to the data. McGaugh (2012) and Fig. 11 of Kroupa (2012). 2.2 The “Graviton Picture” 3. DISCUSSION The “graviton picture” (Trippe 2013) employs the “ It is principally the elegance of general relativ- ad-hoc assumption that gravity is mediated by virtual ity theory and its success in solar system tests gravitons with non-zero mass that obey certain reason- that lead us to the bold extrapolation that the gravitational acceleration has the form GM/r2 able rules of interaction. This leads to the formation of 21 26 a “graviton halo” with a mass density profile ρ ∝ r−2 on scales 10 − 10 cm that are relevant for the around a baryonic source mass M0. The total dynam- solar neighborhood, galaxies, clusters of galax- ” ical mass Mtot scales with centripetal acceleration ac, ies, and superclusters. providing a theoretical MDA relation — Binney & Tremaine (1987), Ch. 10.4, p. 635 Historically, the missing mass problem has usu- Mtot a0 =1+8π (5) ally been approached by postulating non-luminous and M0 ac DERIVATION OF MOND 95 Fig. 1.— The transition functions derived from comparison of MOND and “graviton picture”, assuming am = 1.1 × −10 −2 10 m s . a. The inverse of the function µ1(x) vs. ac. b. The function ν1(y) vs. gn. Please note the logarithmic–linear axis scales. These diagrams should be compared to Fig. 10 of Famaey & McGaugh (2012) and Fig. 11 of Kroupa (2012). non-baryonic dark matter (Ostriker & Peebles 1973; The “graviton picture” of gravitation (Trippe 2013) Einasto et al. 1974), eventually evolving into the starts off from a physical mechanism: the (ad-hoc) as- ΛCDM standard model of cosmology (e.g., Bahcall et sumption that gravity is mediated by virtual massive al. 1999). In recent years, it has become clear that this gravitons that obey certain rules of interaction. From approach is incomplete.
Load more

Recommended publications
  • Adrien Christian René THOB
    THE RELATIONSHIP BETWEEN THE MORPHOLOGY AND KINEMATICS OF GALAXIES AND ITS DEPENDENCE ON DARK MATTER HALO STRUCTURE IN SIMULATED GALAXIES Adrien Christian René THOB A thesis submitted in partial fulfilment of the requirements of Liverpool John Moores University for the degree of Doctor of Philosophy. 26 April 2019 To my grand-parents, René Roumeaux, Christian Thob, Yvette Roumeaux (née Bajaud) and Anne-Marie Thob (née Léglise). ii Abstract Galaxies are among nature’s most majestic and diverse structures. They can play host to as few as several thousands of stars, or as many as hundreds of billions. They exhibit a broad range of shapes, sizes, colours, and they can inhabit vastly differing cosmic environments. The physics of galaxy formation is highly non-linear and in- volves a variety of physical mechanisms, precluding the development of entirely an- alytic descriptions, thus requiring that theoretical ideas concerning the origin of this diversity are tested via the confrontation of numerical models (or “simulations”) with observational measurements. The EAGLE project (which stands for Evolution and Assembly of GaLaxies and their Environments) is a state-of-the-art suite of such cos- mological hydrodynamical simulations of the Universe. EAGLE is unique in that the ill-understood efficiencies of feedback mechanisms implemented in the model were calibrated to ensure that the observed stellar masses and sizes of present-day galaxies were reproduced. We investigate the connection between the morphology and internal 9:5 kinematics of the stellar component of central galaxies with mass M? > 10 M in the EAGLE simulations. We compare several kinematic diagnostics commonly used to describe simulated galaxies, and find good consistency between them.
    [Show full text]
  • Particle Dark Matter an Introduction Into Evidence, Models, and Direct Searches
    Particle Dark Matter An Introduction into Evidence, Models, and Direct Searches Lecture for ESIPAP 2016 European School of Instrumentation in Particle & Astroparticle Physics Archamps Technopole XENON1T January 25th, 2016 Uwe Oberlack Institute of Physics & PRISMA Cluster of Excellence Johannes Gutenberg University Mainz http://xenon.physik.uni-mainz.de Outline ● Evidence for Dark Matter: ▸ The Problem of Missing Mass ▸ In galaxies ▸ In galaxy clusters ▸ In the universe as a whole ● DM Candidates: ▸ The DM particle zoo ▸ WIMPs ● DM Direct Searches: ▸ Detection principle, physics inputs ▸ Example experiments & results ▸ Outlook Uwe Oberlack ESIPAP 2016 2 Types of Evidences for Dark Matter ● Kinematic studies use luminous astrophysical objects to probe the gravitational potential of a massive environment, e.g.: ▸ Stars or gas clouds probing the gravitational potential of galaxies ▸ Galaxies or intergalactic gas probing the gravitational potential of galaxy clusters ● Gravitational lensing is an independent way to measure the total mass (profle) of a foreground object using the light of background sources (galaxies, active galactic nuclei). ● Comparison of mass profles with observed luminosity profles lead to a problem of missing mass, usually interpreted as evidence for Dark Matter. ● Measuring the geometry (curvature) of the universe, indicates a ”fat” universe with close to critical density. Comparison with luminous mass: → a major accounting problem! Including observations of the expansion history lead to the Standard Model of Cosmology: accounting defcit solved by ~68% Dark Energy, ~27% Dark Matter and <5% “regular” (baryonic) matter. ● Other lines of evidence probe properties of matter under the infuence of gravity: ▸ the equation of state of oscillating matter as observed through fuctuations of the Cosmic Microwave Background (acoustic peaks).
    [Show full text]
  • DARK MATTER and NEUTRINOS Arxiv:1711.10564V1 [Physics.Pop-Ph]
    Physics Education 1 dateline DARK MATTER AND NEUTRINOS Gazal Sharma1, Anu2 and B. C. Chauhan3 Department of Physics & Astronomical Science School of Physical & Material Sciences Central University of Himachal Pradesh (CUHP) Dharamshala, Kangra (HP) INDIA-176215. [email protected] [email protected] [email protected] (Submitted 03-08-2015) Abstract The Keplerian distribution of velocities is not observed in the rotation of large scale structures, such as found in the rotation of spiral galaxies. The deviation from Keplerian distribution provides compelling evidence of the presence of non-luminous matter i.e. called dark matter. There are several astrophysical motivations for investigating the dark matter in and around the galaxy as halo. In this work we address various theoretical and experimental indications pointing towards the existence of this unknown form of matter. Amongst its constituents neutrino is one of the most prospective candidates. We know the neutrinos oscillate and have tiny masses, but there are also signatures for existence of heavy and light sterile neutrinos and possibility of their mixing. Altogether, the role of neutrinos is of great interests in cosmology and understanding dark matter. arXiv:1711.10564v1 [physics.pop-ph] 23 Nov 2017 1 Introduction revealed in 2013 that our Universe contains 68:3% of dark energy, 26:8% of dark matter, and only 4:9% of the Universe is known mat- As a human being the biggest surprise for us ter which includes all the stars, planetary sys- was, that the Universe in which we live in tems, galaxies, and interstellar gas etc.. This is mostly dark.
    [Show full text]
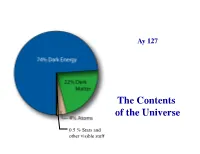
  • The Contents of the Universe
    Ay 127! The Contents of the Universe 0.5 % Stars and other visible stuff Supernovae alone ⇒ Accelerating expansion ⇒ Λ > 0 CMB alone ⇒ Flat universe ⇒ Λ > 0 Any two of SN, CMB, LSS ⇒ Dark energy ~70% Also in agreement with the age estimates (globular clusters, nucleocosmochronology, white dwarfs) Today’s Best Guess Universe Age: Best fit CMB model - consistent with ages of oldest stars t0 =13.82 ± 0.05 Gyr Hubble constant: CMB + HST Key Project to -1 -1 measure Cepheid distances H0 = 69 km s Mpc € Density of ordinary matter: CMB + comparison of nucleosynthesis with Lyman-a Ωbaryon = 0.04 € forest deuterium measurement Density of all forms of matter: Cluster dark matter estimate CMB power spectrum 0.31 € Ωmatter = Cosmological constant: Supernova data, CMB evidence Ω = 0.69 for a flat universe plus a low € Λ matter density € The Component Densities at z ~ 0, in critical density units, assuming h ≈ 0.7 Total matter/energy density: Ω0,tot ≈ 1.00 From CMB, and consistent with SNe, LSS From local dynamics and LSS, and Matter density: Ω0,m ≈ 0.31 consistent with SNe, CMB From cosmic nucleosynthesis, Baryon density: Ω0,b ≈ 0.045 and independently from CMB Luminous baryon density: Ω0,lum ≈ 0.005 From the census of luminous matter (stars, gas) Since: Ω0,tot > Ω0,m > Ω0,b > Ω0,lum There is baryonic dark matter There is non-baryonic dark matter There is dark energy The Luminosity Density Integrate galaxy luminosity function (obtained from large redshift surveys) to obtain the mean luminosity density at z ~ 0 8 3 SDSS, r band: ρL = (1.8 ± 0.2) 10 h70 L/Mpc 8 3 2dFGRS, b band: ρL = (1.4 ± 0.2) 10 h70 L/Mpc Luminosity To Mass Typical (M/L) ratios in the B band along the Hubble sequence, within the luminous portions of galaxies, are ~ 4 - 5 M/L This includes some dark matter - for pure stellar populations, (M/L) ratios should be slightly lower.
    [Show full text]
  • Modified Newtonian Dynamics, an Introductory Review
    Modified Newtonian Dynamics, an Introductory Review Riccardo Scarpa European Southern Observatory, Chile E-mail [email protected] Abstract. By the time, in 1937, the Swiss astronomer Zwicky measured the velocity dispersion of the Coma cluster of galaxies, astronomers somehow got acquainted with the idea that the universe is filled by some kind of dark matter. After almost a century of investigations, we have learned two things about dark matter, (i) it has to be non-baryonic -- that is, made of something new that interact with normal matter only by gravitation-- and, (ii) that its effects are observed in -8 -2 stellar systems when and only when their internal acceleration of gravity falls below a fix value a0=1.2×10 cm s . Being completely decoupled dark and normal matter can mix in any ratio to form the objects we see in the universe, and indeed observations show the relative content of dark matter to vary dramatically from object to object. This is in open contrast with point (ii). In fact, there is no reason why normal and dark matter should conspire to mix in just the right way for the mass discrepancy to appear always below a fixed acceleration. This systematic, more than anything else, tells us we might be facing a failure of the law of gravity in the weak field limit rather then the effects of dark matter. Thus, in an attempt to avoid the need for dark matter many modifications of the law of gravity have been proposed in the past decades. The most successful – and the only one that survived observational tests -- is the Modified Newtonian Dynamics.
    [Show full text]
  • Baryonic and Non-Baryonic Dark Matter in Massive Galaxies
    Baryonic and Non-Baryonic Dark Matter: Halo Contraction and the IMF Matt Auger UC Santa Barbara Tommaso Treu, Raphael Gavazzi, Adam Bolton, Leon Koopmans, Phil Marshall Refrain: Strong Gravitational Lensing Background Source Multiply-Imaged by Massive Foreground Galaxy Image Separation depends on: - lens and source redshifts (geometry) - lensing galaxy mass First Verse: The Sloan Lens ACS (SLACS) Survey SLACS Strong Lens Factory Late-type Background Source Early-type Foreground Lens SLACS Strong Lens Factory [OII] from source Ca K&H from Lens Second Verse: Properties of Early-Type Galaxies ETGs show remarkably tight scaling relations between size, velocity dispersion and ... FP M*P MP Surface Stellar mass Total mass brightness density density Hyper-plane Relations Relationship between: - size - velocity dispersion - total mass in Re/2 - stellar mass Consistent with no intrinsic scatter, no dependence on stellar mass More Massive Galaxies have More Central Dark Matter Total M/L M/L `dark' matter Stellar M/L mass Dark Matter could be CDM or could be baryons not described by the IMF Third Verse: The Important Physical Properties and Mechanisms Three Key Ingredients - Star-formation efficiency (mass dependent) - Dark matter (response to baryons?) - IMF (mass-dependent ??) Star Formation Efficiency Increasing Satellite kinematics efficiency and weak lensing broadly confirm the expected trends of decreased eff. at high and low mass due to feedback from AGN and stars Dutton et al 2010 Abundance Matching Moster et al 2010 Cold Dark Matter Halo NFW Halos from N-body Simulations ETGs are dominated by baryons at small radii Cold Dark Matter Halo Cooling of baryons causes the halo to contract Gnedin et al 2004 Cold Dark Matter Halo Halo contraction may depend on the amount of baryons and how the baryons got there Dynamical friction can `puff up' halos..
    [Show full text]
  • Baryonic and Non-Baryonic Dark Matter
    Baryonic and Non-Baryonic Dark Mat- ter Bernard CARR Astronomy Unit, Queen Mary & Westfield College, Mile End Road, London E1 4NS, England, [email protected] Abstract Cosmological nucleosynthesis calculations imply that there should be both non-baryonic and baryonic dark matter. Recent data suggest that some of the non-baryonic dark matter must be “hot” (i.e. massive neutrinos) and there may also be evidence for “cold” dark matter (i.e. WIMPs). If the baryonic dark matter resides in galactic halos, it is likely to be in the form of compact objects (i.e. MACHOs) and these would probably be the remnants of a first generation of pregalactic or protogalactic Population III stars. Many candidates have been proposed - brown dwarfs, red dwarfs, white dwarfs or black holes - and at various times each of these has been in vogue. We review the many types of observations which can be used to constrain or exclude both baryonic and non-baryonic dark matter candidates. 1. Introduction arXiv:gr-qc/0008005v1 1 Aug 2000 Evidence for dark matter has been claimed in many different contexts. There may be local dark matter in the Galactic disc, dark matter in the halos of our own and other galaxies, dark matter associated with clusters of galaxies and finally - if one believes that the total cosmological density has the critical value - smoothly distributed background dark matter. Since dark matter probably takes as many different forms as visible matter, it would be simplistic to assume that all these dark matter problems have a single solution. The local dark matter is almost certainly unrelated to the other ones and, while the halo and cluster dark matter would be naturally connected in many evolutionary scenarios, there is a growing tendency to regard the unclustered background dark matter as different from the clustered component.
    [Show full text]
  • Determining Properties of LEGA-C Galaxies Through Spectral Star-Formation History Reconstruction
    Determining Properties of LEGA-C Galaxies through Spectral Star-formation History Reconstruction Priscilla Chauke Dissertation submitted to the Combined Faculties for the Natural Sciences and for Mathematics of the Ruperto-Carola University of Heidelberg, Germany for the degree of Doctor of Natural Sciences Put forward by Priscilla Chauke Born in Giyani, South Africa Oral Examination: 24 July 2019 Determining Properties of LEGA-C Galaxies through Spectral Star-formation History Reconstruction Referees: Prof. Dr. Arjen van der Wel Prof. Dr. Jochen Heidt Va ka hina “My work amounts to a drop in a limitless ocean. Yet what is any ocean, but a multitude of drops?” -Adapted from David Mitchell, Cloud Atlas Acknowledgements I thank Arjen van der Wel for giving me the opportunity to pursue a PhD at the Max Planck Institut für Astronomy and for being my advisor throughout the years. I thank IMPRS and the DAAD for supporting me financially for the last four years. Lastly, I thank my family and friends for their love, support and encouragement. Abstract Over the past decade, photometric and spectroscopic surveys have enabled us to obtain an integrated view of galaxy evolution. We have measured the cosmic star formation history, and we know that about half of the stars we observe formed before the Universe was half of its current age. However, crucial knowledge of individual galaxy evolution has been limited because the detailed stellar population proper- ties that we know about galaxies, such as ages, metallicities and kinematics, have mostly been obtained from nearby galaxies, which contain mostly old stellar popu- lations.
    [Show full text]
  • Non-Baryonic Dark Matter
    FR9703177 Institut Universite Claude Bernard de Physique IN2P3 - CNRS Nucleaire de Lyon LYCEN 9643 D6cembre 1996 Non-Baryonic Dark Matter Ecole Internationale de Cosmologie, Casablanca, 1-10 decembre 1996 I. Berk&s Institut de Physique Nucleaire de Lyon, IN2P3/CNRS, Universite Claude Bernard, F-69622 Villeuibanne Cedex, France 43, Boulevard du 11 Novembre 1918 - 69622 V1LLEURBANNE Cedex - France NON-BARYONIC DARK MATTER. (*) I. Berkes IPNL, Universite Lyon I et IN2P3, F-69622 VILLEURBANNE CEDEX Abstract. This article discusses the nature of the dark matter and the possibility of the detection of non-baryonic dark matter in an underground experiment. Among the useful detectors the low tem­ perature bolometers are considered in some detail. Resume. Get article expose les differences hypotheses sur la nature de la matiere noire, et la possibility de la detection de la matidre noire non-baryonique dans une experience souterraine. Parmi les de- tecteurs envisages 1'accent est mis sur les bolometres travaillant h. basse temperature. 1) Galactic dark matter. The best known star in our Galaxy is the Sun. Its mass is about Mo=2xl0 j0 kg, and it radiates a power of L©=3.8x10W. The ratio of these two quantities is Mo/Lo = 5200 kg/W. In our Galaxy masses for binary stars can be determined from their relative movement. It comes out, that while M and L vary strongly from a star to another, the ratio M/L varies only slightly for stars in the main sequence. So, the luminosity may be used as a mesure o the mass of a star, super-giants, white dwarfs, black holes and other exoti objects excepted.
    [Show full text]
  • Dark Matter in the Universe
    A UNIVERSAL VIEW Dark Matter in the Universe by Vera Rubin AND NASA Space Telescope Science Institute Science Telescope Space BRAD WHITMORE Carnegie Institution of Washington, Carnegie FRANÇOIS SCHWEIZER As much as 90 percent of the matter in the universe is invisible. Detecting this dark matter will help astronomers better comprehend the universeÕs destiny 106 Scientific American Presents Dark Matter in the Universe Copyright 1998 Scientific American, Inc. magine, for a moment, that one night you awaken is that our understanding of gravity needs a major revision—but abruptly from a dream. Coming to consciousness, blink- most physicists do not consider that option seriously. ing your eyes against the blackness, you find that, inexpli- In some sense, our ignorance about dark matter’s properties cably, you are standing alone in a vast, pitch-black cav- has become inextricably tangled up with other outstanding ern. Befuddled by this predicament, you wonder: Where am I? issues in cosmology—such as how much mass the universe con- What is this space? What are its dimensions? tains, how galaxies formed and whether or not the universe will IGroping in the darkness, you stumble upon a book of expand forever. So important is this dark matter to our under- damp matches. You strike one; it quickly flares, then fizzles standing of the size, shape and ultimate fate of the universe that out. Again, you try; again, a flash and fizzle. But in that mo- the search for it will very likely dominate astronomy for the ment, you realize that you can glimpse a bit of your sur- next few decades.
    [Show full text]
  • Asymmetric Dark Matter
    Asymmetric Dark Matter Joshua Berger We present notes on asymmetric dark matter (ADM), with a particular focus on elaborating on the points made in [1]. We focus undestanding how to derive cosmological properties of general models of dark matter, as well as particle physics and cosmological considerations that must be taken into account when working with models of ADM. We also summarize some possible signatures of models of ADM and mention some follow up work on the subject. 2 Component Ω Cosmological Constant/Dark Energy 0.742 Dark Matter 0.214 Baryonic Matter 0.0441 TABLE I. Energy distributions of the major components of the universe relative to the critical density ρcrit ∼ 1. I. MOTIVATION Recent results from cosmological observations have led to several new puzzles. It is possible that some of these puzzles are connected to the major puzzles of particle physics at the weak scale. One such puzzle that may be plausibly connected to the weak scale relates to the abundances of particles in the universe. Using data from astrophysical observations from several sources, including the CMB specturm, structure on super-galactic scales, and redshifts of distant luminous sources, the relative energy density distributions of the major components of the present-day universe have been determined accurately[2], as shown in Table I. Note that three components of the universe that we might think are unrelated all have contributions within an order of magnitude of each other. The order 1 contribution of the cosmological constant could plausibly be a coincidence, albeit a very striking one, since its contribution was small in the early universe and only relatively recently on cosmological scales became important.
    [Show full text]
  • Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S
    Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S. Mcgaugh To cite this version: Benoit Famaey, Stacy S. Mcgaugh. Modified Newtonian Dynamics (MOND): Observational Phe- nomenology and Relativistic Extensions. Living Reviews in Relativity, 2012, 15 (1), 10.12942/lrr- 2012-10. hal-02927744 HAL Id: hal-02927744 https://hal.archives-ouvertes.fr/hal-02927744 Submitted on 1 Sep 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Living Rev. Relativity, 15, (2012), 10 LIVINGREVIEWS http://www.livingreviews.org/lrr-2012-10 in relativity Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Beno^ıtFamaey Observatoire Astronomique de Strasbourg CNRS, UMR 7550, France and AIfA, University of Bonn, Germany email: [email protected] http://astro.u-strasbg.fr/~famaey/ Stacy S. McGaugh Department of Astronomy University of Maryland, USA and Case Western Reserve University, USA email: [email protected] http://astroweb.case.edu/ssm/ Accepted on 30 April 2012 Published on 7 September 2012 Abstract A wealth of astronomical data indicate the presence of mass discrepancies in the Universe. The motions observed in a variety of classes of extragalactic systems exceed what can be explained by the mass visible in stars and gas.
    [Show full text]