River Engineering John Fenton
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Geomorphic Classification of Rivers
9.36 Geomorphic Classification of Rivers JM Buffington, U.S. Forest Service, Boise, ID, USA DR Montgomery, University of Washington, Seattle, WA, USA Published by Elsevier Inc. 9.36.1 Introduction 730 9.36.2 Purpose of Classification 730 9.36.3 Types of Channel Classification 731 9.36.3.1 Stream Order 731 9.36.3.2 Process Domains 732 9.36.3.3 Channel Pattern 732 9.36.3.4 Channel–Floodplain Interactions 735 9.36.3.5 Bed Material and Mobility 737 9.36.3.6 Channel Units 739 9.36.3.7 Hierarchical Classifications 739 9.36.3.8 Statistical Classifications 745 9.36.4 Use and Compatibility of Channel Classifications 745 9.36.5 The Rise and Fall of Classifications: Why Are Some Channel Classifications More Used Than Others? 747 9.36.6 Future Needs and Directions 753 9.36.6.1 Standardization and Sample Size 753 9.36.6.2 Remote Sensing 754 9.36.7 Conclusion 755 Acknowledgements 756 References 756 Appendix 762 9.36.1 Introduction 9.36.2 Purpose of Classification Over the last several decades, environmental legislation and a A basic tenet in geomorphology is that ‘form implies process.’As growing awareness of historical human disturbance to rivers such, numerous geomorphic classifications have been de- worldwide (Schumm, 1977; Collins et al., 2003; Surian and veloped for landscapes (Davis, 1899), hillslopes (Varnes, 1958), Rinaldi, 2003; Nilsson et al., 2005; Chin, 2006; Walter and and rivers (Section 9.36.3). The form–process paradigm is a Merritts, 2008) have fostered unprecedented collaboration potentially powerful tool for conducting quantitative geo- among scientists, land managers, and stakeholders to better morphic investigations. -

Stream Restoration, a Natural Channel Design
Stream Restoration Prep8AICI by the North Carolina Stream Restonltlon Institute and North Carolina Sea Grant INC STATE UNIVERSITY I North Carolina State University and North Carolina A&T State University commit themselves to positive action to secure equal opportunity regardless of race, color, creed, national origin, religion, sex, age or disability. In addition, the two Universities welcome all persons without regard to sexual orientation. Contents Introduction to Fluvial Processes 1 Stream Assessment and Survey Procedures 2 Rosgen Stream-Classification Systems/ Channel Assessment and Validation Procedures 3 Bankfull Verification and Gage Station Analyses 4 Priority Options for Restoring Incised Streams 5 Reference Reach Survey 6 Design Procedures 7 Structures 8 Vegetation Stabilization and Riparian-Buffer Re-establishment 9 Erosion and Sediment-Control Plan 10 Flood Studies 11 Restoration Evaluation and Monitoring 12 References and Resources 13 Appendices Preface Streams and rivers serve many purposes, including water supply, The authors would like to thank the following people for reviewing wildlife habitat, energy generation, transportation and recreation. the document: A stream is a dynamic, complex system that includes not only Micky Clemmons the active channel but also the floodplain and the vegetation Rockie English, Ph.D. along its edges. A natural stream system remains stable while Chris Estes transporting a wide range of flows and sediment produced in its Angela Jessup, P.E. watershed, maintaining a state of "dynamic equilibrium." When Joseph Mickey changes to the channel, floodplain, vegetation, flow or sediment David Penrose supply significantly affect this equilibrium, the stream may Todd St. John become unstable and start adjusting toward a new equilibrium state. -

Is Hydrology Kinematic?
HYDROLOGICAL PROCESSES Hydrol. Process. 16, 667–716 (2002) DOI: 10.1002/hyp.306 Is hydrology kinematic? V. P. Singh* Department of Civil and Environmental Engineering, Louisiana State University, Baton Rouge, LA 70803-6405, USA Abstract: A wide range of phenomena, natural as well as man-made, in physical, chemical and biological hydrology exhibit characteristics similar to those of kinematic waves. The question we ask is: can these phenomena be described using the theory of kinematic waves? Since the range of phenomena is wide, another question we ask is: how prevalent are kinematic waves? If they are widely pervasive, does that mean hydrology is kinematic or close to it? This paper addresses these issues, which are perceived to be fundamental to advancing the state-of-the-art of water science and engineering. Copyright 2002 John Wiley & Sons, Ltd. KEY WORDS biological hydrology; chemical hydrology; physical hydrology; kinematic wave theory; kinematics; flux laws INTRODUCTION There is a wide range of natural and man-made physical, chemical and biological flow phenomena that exhibit wave characteristics. The term ‘wave’ implies a disturbance travelling upstream, downstream or remaining stationary. We can visualize a water wave propagating where the water itself stays very much where it was before the wave was produced. We witness other waves which travel as well, such as heat waves, pressure waves, sound waves, etc. There is obviously the motion of matter, but there can also be the motion of form and other properties of the matter. The flow phenomena, according to the nature of particles composing them, can be distinguished into two categories: (1) flows of discrete noncoherent particles and (2) flows of continuous coherent particles. -
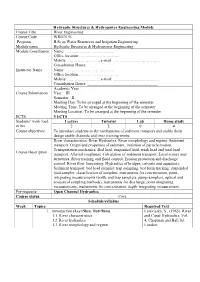
Hydraulic Structures & Hydropower Engineering Module Course Title
Hydraulic Structures & Hydropower Engineering Module Course Title River Engineering Course Code WRIE3151 Program B.Sc in Water Resources and Irrigation Engineering Module name Hydraulic Structures & Hydropower Engineering Module Coordinator Name: . …………………………….. Office location . ……………………….. Mobile: . ………………….; e-mail: ……………………………. Consultation Hours: Instructor Name Name: . …………………………….. Office location . ……………………….. Mobile: . ………………….; e-mail: ……………………………. Consultation Hours: Academic Year Course Information Year: III Semester : II Meeting Day: To be arranged at the beginning of the semester Meeting Time: To be arranged at the beginning of the semester Meeting Location: To be arranged at the beginning of the semester ECTS 5 ECTS Students’ work load Lecture Tutorial Lab Home study in hrs 2 2 0 4 Course objectives To introduce students to the mechanisms of sediment transport and enable them design stable channels and river training works. River characteristics. River Hydraulics. River morphology and regime. Sediment transport: Origin and properties of sediment, initiation of particle motion. Transportation mechanics, Bed load, suspended load, wash load and total load Course Description transport. Alluvial roughness. Calculation of sediment transport. Local scours near structures. River training and flood control. Erosion protection and discharge control. River flow forecasting. Hydraulics of bridges, culverts and aqueducts. Sediment transport: bed load sampler: trap sampling, bed form tracking; suspended load sampler: classification of samplers, instruments for concentration, point- integrating measurements (bottle and trap samplers, pump-samplers, optical and acoustical sampling methods), instruments for discharge, point integrating measurements, instruments for concentration, depth-integrating measurement. Pre-requisite Open Channel Hydraulics Course status Core Schedule/syllabus Week Topics Required Text 1. Introduction (Lec=5hrs, Tut=5hrs) Lelaviasky, S., (1965). River 1.1 River characteristics and Canal Hydraulics, Vol. -

River and Environmental Processes in the Wetland Restoration of the Morava River
Transactions on Ecology and the Environment vol 50, © 2001 WIT Press, www.witpress.com, ISSN 1743-3541 River and environmental processes in the wetland restoration of the Morava river K. ~olubova'8: M. J. ~isickJ '~~drologyDepartment, Water Research Institute, Bratislava, Slovakia 2~~~~~~o~l~gyand Monitoring Department, Institute of Zoology SAS, Bratislava, Slovakia Abstract fiver engineering works and other man-induced changes may adversely affect natural character of the river system. In many cases they have caused major morphological and ecological instability problems which can seriously impair the conservation and amenity value of the riverine environment. The results of two projects focused at the restoration of the Morava wetland ecosystem are presented in this paper. Impact of the river regulation is analysed on the basis of defined river processes and ecology evaluation. Monitoring of biotic and abiotic changes provided background information for evaluation of efficiency of the former meander's restoration. As implemented restoration measures were not so effective as it was expected some alternatives of improvements are discussed with regard to the results of field observations, numerical and physical modeling. An optimal solution to protect the oxbow system against successive degradation and restore some extinct river functions is presented. 1 Introduction The Morava river is one of the largest Danube tributaries. The lower part of the Morava basin creates a natural wetland ecosystem with valuable floodplain landscape, which is unique in Central Europe. lkspart of the river floodplain is bordered by the Dyje river, which is the main tributary of the Morava river and by confluence with the Danube river. -

Guidance for Stream Restoration and Rehabilitation
United States Department of Agriculture Guidance for Stream Restoration and Rehabilitation Steven E. Yochum Forest National Stream & Technical Note Service Aquatic Ecology Center TN-102.2 May 2016 Yochum, Steven E. 2016. Guidance for Stream Restoration and Rehabilitation. Technical Note TN-102.2. Fort Collins, CO: U.S. Department of Agriculture, Forest Service, National Stream & Aquatic Ecology Center Cover Photos: Top-right: Illinois River, North Park, Colorado. Photo by Steven Yochum Bottom-left: Whychus Creek, Oregon. Photo by Paul Powers ABSTRACT A great deal of effort has been devoted to developing guidance for stream restoration and rehabilitation. The available resources are diverse, reflecting the wide ranging approaches used and expertise required to develop stream restoration projects. To help practitioners sort through all of this information, a technical note has been developed to provide a guide to the wealth of information available. The document structure is primarily a series of short literature reviews followed by a hyperlinked reference list for the reader to find more information on each topic. The primary topics incorporated into this guidance include general methods, an overview of stream processes and restoration, case studies, and methods for data compilation, preliminary assessments, and field data collection. Analysis methods and tools, and planning and design guidance for specific restoration features, are also provided. This technical note is a bibliographic repository of information available to assist professionals with the process of planning, analyzing, and designing stream restoration and rehabilitation projects. U.S. Forest Service NSAEC TN-102.2 Fort Collins, Colorado Guidance for Stream Restoration & Rehabilitation i of v May 2016 ADVISORY NOTE Techniques and approaches contained in this handbook are not all-inclusive, nor universally applicable. -

1. Introduction
Introduction Inland Waterway Transport (IWT) is an important mode of transportation. In most situations it has the advantageof the least cost, least energy consumption and land saving, as compared to other modes of transportation. The order of the ratios between water, railway and road transportation is within the ranges of 1:2:5 in cost and 1:1.5:4 in energy consumption respectively. Although IWT is not as fast as railway or highway, it continues to be competitive for transportation of bulk products in fully developed countries such as the United States and European countries. In some developing countries today land routes are virtually nonexistent in some areas, and the simple roads or trails that do exist are inadequate for commercial transportation, especially in the rainy season. In such areas inland waterways are extremely important as transportation routes for people and supplies. The total length of waterways in Asia is about 167,000 kIn or one third of the world's total. IWT obviously is an important resource for Asian countries. The improvement and development of IWT will surely assistthe development and improvement of efficiency of waterborne commerce, and promote the expansion of existing production and development of new industrial and agricultural production. In short, improved commercial IWT can support the ..economic development of a region and, therefore, of the nation. ""; OF INLAND WATERWAYS Inland navigation channels for commercial traffic are generally of three types: open river waterways, canalized waterways, and canals. The choice of the type for any river, or any reach of a river, is determined by local conditions and finally by cost if more than one type of development is suitable. -

The Management of the Mississippi River System
The management of the Mississippi Jonathan W.F. Remo Associate Professor River System: an engineered legacy Director of Env. & Policy Program with a flood of future policy challenges Debris Removal “River Training” Greenville Mississippi 1927 Social Template: Management of the Mississippi River and its Major Tributaries Navigation – Commerce Clause – River and Harbors Act, 1824 Flood Control Act - 1928 Gavin's Point Dam, Missouri River Endangered Pallid Sturgeon Water Supply, Flood Control, and Power Generation - Flood NEPA, ESA – late 1960s – early 1970s and 1986 WRDA and Control Act of 1944 – Pick Sloan Missouri Basin Program Environmental Management Program - River Rehabilitation The Engineering Tool Kit: Navigation - River Training The Engineering Tool Kit: Navigation - Locks and Dams Lock and Dam Number 8 – La Crosse Wisconsin The Engineering Tool Kit: Navigation and Flood Risk Reduction - Reservoirs • 40,000 Reservoirs • ~440 km3 of storage • 1% of these dams account for 89% of storage Reservoir Impacts on Peak Flood Discharges Estimated Flood Peak Reduction by Model Reduction of Flood Discharges Reservoirs for the 1973 and 2011 Floods at St. Louis (USACE, 2004) (USACE, 1973 and DeHaan et al., 2012) Percent Chance Flood Peak Reduction Discharge Reduction Station Exceedance 1973 2011 0.2 -12% Alton -4% No Data 0.5 -15% St. Louis -6% No Data 1 -18% Cairo -15% <-2% 2 -17% Memphis -13% No Data 5 -17% 10 -18% Arkansas City -8% No Data 20 -17% Vicksburg -7% No Data 50 -19% Natchez -6% No Data Reservoir Impact on River Flows 25% - moderate -

Chapter 8 Contents
8 Design of river and canal structures 1 2 3 4 5 6 7 8 9 10 CIRIA C683 965 8 Design of river and canal structures CHAPTER 8 CONTENTS 8.1 Introduction. 970 8.1.1 Context . 970 8.1.2 Types of structures and functions. 971 8.1.3 Design methodolology. 973 8.1.3.1 Approach to the design . 973 8.1.3.2 Functional requirements . 974 8.1.3.3 Detailed design . 975 8.1.3.4 Economic considerations . 975 8.1.3.5 Environmental and social considerations . 976 8.1.3.6 Physical conditions . 976 8.1.3.7 Materials related considerations. 977 8.1.3.8 Construction related considerations . 979 8.1.3.9 Operation and maintenance related considerations . 980 8.2 River training works . 980 8.2.1 Erosion processes . 980 8.2.2 Types of river training structures . 982 8.2.2.1 Revetments . 983 8.2.2.2 Spur-dikes and hard points . 984 8.2.2.3 Guide banks . 985 8.2.2.4 Works to improve navigation . 986 8.2.2.5 Flood protection . 986 8.2.2.6 Selection of the appropriate solution. 987 8.2.3 Data collection . 988 8.2.4 Determination of the loadings . 988 8.2.4.1 Hydraulic loads. 988 8.2.4.2 Other types of loads . 989 8.2.5 Plan layout . 989 8.2.5.1 General points. 989 8.2.5.2 Bank protection . 990 8.2.5.3 Spur-dikes . 992 8.2.5.4 Longitudinal dikes or guide banks . -

Green Approaches in River Engineering Supporting Implementation of Green Infrastructure
Green approaches in river engineering Supporting implementation of Green Infrastructure Green approaches in river engineering Supporting implementation of Green Infrastructure © HR Wallingford Ltd This publication was produced under grant NE/N017560/1 which was awarded by the UK Natural Environment Research Council (NERC). The team was led by HR Wallingford Ltd and comprised Environmental Policy Consulting, the River Restoration Centre, CIRIA, the University of Liverpool and the University of Nottingham. Natural Resources Wales, the Environment Agency, the Welsh Local Government Association and Natural England were partners in this project. Authors Marta Roca (HR Wallingford), Manuela Escarameia (HR Wallingford), Olalla Gimeno (HR Wallingford), Lucas de Vilder (HR Wallingford), Jonathan Simm (HR Wallingford), Bruce Horton (Environmental Policy Consulting), Colin Thorne (University of Nottingham). Contributors: Janet Hooke (University of Liverpool), Martin Janes (River Restoration Centre), Marc Naura (River Restoration Centre), Paul Weller (Environment Agency), Owen Tarrant (Environment Agency), Lydia Burgess-Gamble (Environment Agency), Jenny Wheeldon (Natural England), Larissa Naylor (University of Glasgow), Hugh Kippen (University of Glasgow), Helen Stevenson (HR Wallingford). Acknowledgments: Huw Alford (Natural Resources Wales), Martin Coombes (University of Oxford), Simon Cuming (Environment Agency), Wyn Davies (Natural Resources Wales), Jean-Francois Dulong (Welsh Local Government Association), Heather Forbes (SEPA), James Galsworthy (Natural Resources Wales), Victoria Greest (Natural Resources Wales), David Holland (Salix River & Wetland Services Ltd), Rachel Hunt (Environment Agency), Adrian Jones (Natural Resources Wales), Oly Lowe (Natural Resources Wales), Tim Martin (Greenfix), Fiona Moore (Land & Water Services Ltd), James Neal (Natural Resources Wales), John Phillips (Environment Agency), Lynn Puttock (Terraqua Environmental Services), Emma Thompson (Environment Agency), Dave Webb (Environment Agency). -

Guidance for Stream Restoration
United States Department of Agriculture Guidance for Stream Restoration Steven E. Yochum Forest National Stream & Technical Note Service Aquatic Ecology Center TN-102.4 May 2018 Yochum, Steven E. 2018. Guidance for Stream Restoration. U.S. Department of Agriculture, Forest Service, National Stream & Aquatic Ecology Center, Technical Note TN-102.4. Fort Collins, CO. Cover Photos: Top-right: Illinois River, North Park, Colorado. Photo by Steven Yochum Bottom-left: Whychus Creek, Oregon. Photo by Paul Powers ABSTRACT A great deal of effort has been devoted to developing guidance for stream restoration. The available resources are diverse, reflecting the wide ranging approaches used and expertise required to develop effective stream restoration projects. To help practitioners sort through the extensive information, this technical note has been developed to provide a guide to the available guidance. The document structure is primarily a series of short literature reviews followed by a hyperlinked reference list for readers to find more information on each topic. The primary topics incorporated into this guidance include general methods, an overview of stream processes and restoration, case studies, data compilation, preliminary assessments, and field data collection. Analysis methods and tools, and planning and design guidance for specific restoration features are also provided. This technical note is a bibliographic repository of information available to assist professionals with the process of planning, analyzing, and designing stream restoration projects. U.S. Forest Service NSAEC TN-102.4 Fort Collins, Colorado Guidance for Stream Restoration & Rehabilitation i of vi May 2018 ADVISORY NOTE Techniques and approaches contained in this technical note are not all-inclusive, nor universally applicable. -

Sample Review Problems on River Engineering
CIVE 413 - ENVIRONMENTAL RIVER MECHANICS Pierre Y. Julien April 2 1,2008 Sample Review Problems on River Engineering 1. Consider a large river during a flood. The main channel width is 250 m, the flow depth is 6.62 m and the flow velocity is 2.26 ds. The channel slope is 10 crnlkrn and the grain diameter is uniform 0.25 mm sand. Determine the following: a. the Froude number b. Manning n c. the bed shear stress d, the Shields parameter e. what particle diameter is at beginning of motion f. what is the settling velocity of the bed material g. what is the shear velocity of the flow h. is most of the sediment transported as bed load or in suspension 2. Bridge piers are built on the river discussed above. The type of bridge pier considered is a square concrete bridge pier 3.5 m wide. Determine the scour depth around the structure. Also estimate the angle of repose of the material and estimate the lateral extent of the scour hole. 3. Repeat the calculations from (2) above for the case of replacing square bridge piers with a large round sheet pile caisson that is 15.2 m in diameter. Determine the scour depth and the lateral extent of the scour hole. \ 4. The engineers are also considering an abutment protruding into the river. Consider a 75 m long spill-through abutment that is normal to the main flow direction. Also consider a 50 m abutment with the same orientation angle with vertical sheet pile wall at the end of the abutment.